不同结构深度神经网络的时间域航空电磁数据成像性能分析

李金峰，刘云鹤

吉林大学 地球探测科学与技术学院，长春 130026

0 引言

反问题一直是地球物理领域的热点研究方向。由于测量数据有限，传统的地球物理反演方法主要为基于正则化思想的优化方法，需要严格的数学计算，耗时较长。时间域航空电磁系统采样密集，数据量巨大，成像技术是其主要的反问题求解方法，在航空电磁的数据处理中占有重要的地位。传统的成像技术得到的模型较为简单[1--3]，获得的地电结构分辨率较低。目前发展较快的深度神经网络技术能够高度提取数据的抽象特征，适合拟合复杂的非线性关系，且计算速度快，有潜力成为航空电磁成像的主流技术。

早在20世纪末，人们就将神经网络技术应用到地球物理领域。刘瑞林等[4]提出用神经网络建立孔隙度预测模型，Murat et al.[5]提出使用神经网络进行波形识别以及初至波拾取， Langer et al.[6]提出使用神经网络进行地震反演，朱凯光等[7]提出使用神经网络对时间域电磁数据进行电导率深度成像，以上研究都是基于传统的神经网络进行的。最新研究[8--9]表明深度神经网络比传统的浅层神经网络有更强大的函数近似能力，且更适合拟合自然函数(非线性函数),所以开展深度神经网络在地球物理领域中应用的研究具有较大的实际意义。

深度神经网络在地球物理领域的应用已经获得了一些比传统的神经网络更实用、更精确的成果。卷积神经网络[10](convolution neural network，CNN)在计算机视觉领域应用广泛，其独特的卷积结构使其擅长进行目标识别、特征提取等工作。地球物理研究者们也利用卷积神经网络的特点进行了一系列的工作，例如地震面波分类、地震断层识别、地球物理特征提取以及异常体边界的圈定等[11--14]。此外，深度神经网络也可以解决多元回归问题，例如，地震速度正反演[15]、电导率深度成像等。神经网络有多种结构，不同结构的神经网络对应不同的泛函空间，因此在解决具体问题之前需要通过实验寻找最优的网络模型。在回归问题中，神经网络的结构选择没有理论依据，笔者从时间域航空电磁数据成像问题出发，利用深度神经网络学习合适的网络参数去拟合地下模型与其响应信号间的映射关系,进而通过神经网络直接从数据得到地下电性结构图像；主要通过测试不同结构神经网络在时间域航空电磁成像上的性能，研究在回归问题中如何选择关键参数来建立合理的神经网络模型，以达到高精度的成像效果。

1 研究方法

神经网络的训练过程实际上是最小化定义在训练集上的损失函数。从训练集中选取n个样本{(xi,yi),i=1,...,n} ,xi为电磁信号数据，yi为地下电阻率模型，其损失函数为:

(1)

式中：L为模型向量yi的长度；Netθ(xi)表示当网络的输入为xi时网络预测的电阻率模型。网络采用误差反向传播算法[16]获得参数的改变量，并通过梯度下降法进行参数更新来最小化损失函数。为了简化问题，使用神经网络预测20个不同深度下的电阻率，即在公式(1)中模型向量的长度为20，对应20个不同深度下的电阻率。使用早停法[17]训练神经网络并使用测试集测试网络性能。早停法的耐心值设为8，通过监控验证集与训练集的损失数值决定是否停止训练。早停法可以增强网络的鲁棒性，使网络可以适用于带有干扰的实测数据。笔者对不同结构深度神经网络的训练及其测试结果进行了分析。

1.1 全连接网络(Dense)

全连接网络结构如图1所示，对于任意中间层，网络的输入为x∈Rd，网络的输出为y∈Rh。输入层与输出层之间使用权重矩阵ω与偏置b相连接，即对于输出层任意元素

x为网络的输入向量；y为网络的输出向量；ω为网络的权重矩阵。图1 全连接网络结构示意图Fig.1 Schematic diagram of full connected network model

(2)

式中：f函数被称为网络的激活函数。在本文的实验中，全连接网络的最后一层使用Sigmoid函数：f(x)=1/(1+e-x)作为激活函数，其余层使用ReLU[10]函数：f(x)=max(x,0)作为激活函数。图2展示了在测试集上，网络层数和每层的神经元数目对网络性能的影响。所有实验中，评价因子均采用网络预测的电阻率与真实电阻率取对数后的平均绝对误差(mean absolute error，MAE)，即公式(1)中的J(θ)。

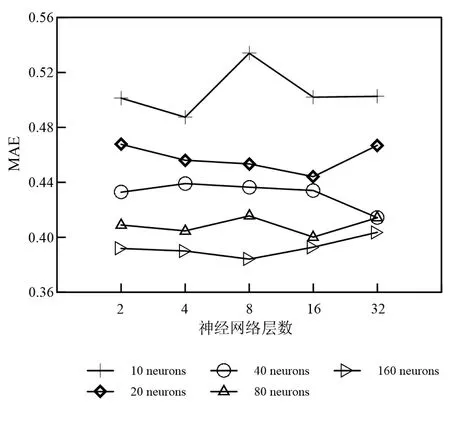
图2 全连接神经网络中网络层数与每层神经元数目对网络性能的影响Fig.2 Influence of network layers and kernel numbers of each convolution on full connected network performance

由图2可知，使用全连接神经网络近似模型电阻率与响应信号之间的映射时，MAE值随网络神经元数目的增加而降低，网络层数对MAE影响不大。最优的全连接网络为8层，每层神经元个数为160。图3为最优的全连接网络在测试集上的表现。

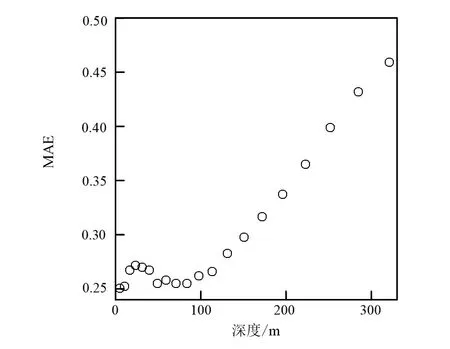
图3 全连接神经网络预测的电阻率与真实电阻率的平均绝对误差(MAE)随深度的变化趋势Fig.3 Changing trend of mean absolute error (MAE) calculated between true resistivity and predicted resistivity by full connected network with depth

由图3可知，全连接神经网络的预测精度大致随着目标深度增加而降低。结果与实际情况相符，因为电磁信号衰减速度快，穿透性差，电磁法勘探精度随深度增加而降低。

1.2 卷积神经网络

卷积神经网络使用卷积核进行运算，层与层之间通过卷积核相连，其特点之一是局部连接性。对于自然图像而言，相临的像素关联性强，较远的像素间相关性弱，卷积神经网络的局部连接特性刚好符合自然图像的这一规律，所以被广泛应用于计算机视觉领域。对于时间域电磁数据而言，相邻时间道关联性强，因为其包含的信息是相近的，距离较远的时间道关联性较弱，这也满足卷积神经网络的局部连接特性。

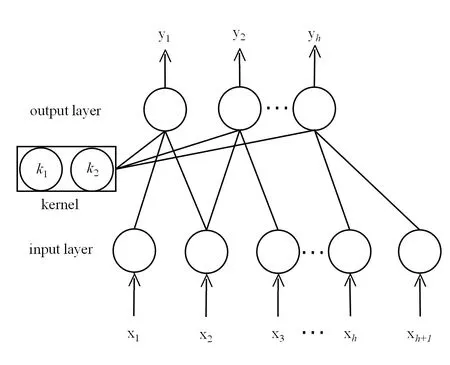
图4 一维卷积神经网络的局部结构Fig.4 Local structure of 1 D convolution neural network

一维卷积神经网络的基本结构如图4所示，设定卷积核的移动步长为1，卷积核的大小为2。因此，对于任意中间层，网络的输入为x,x∈Rh-1，网络的输出为y,y∈Rh。网络的输入信号通过与卷积核相卷积得到网络输出, 对于输出层的任意元素：

yi=f(k1+xi+k2xi+1b)

(3)

式中：f为激活函数；b为网络偏置。在卷积神经网络最后一层加入20个神经元的全连接网络，对应预测20个不同深度的电阻率，卷积层的激活函数为ReLU函数，全连接层的激活函数为Sigmoid。使用测试集测试网络层数和每层卷积核数目对网络性能的影响，实验结果如图5所示。

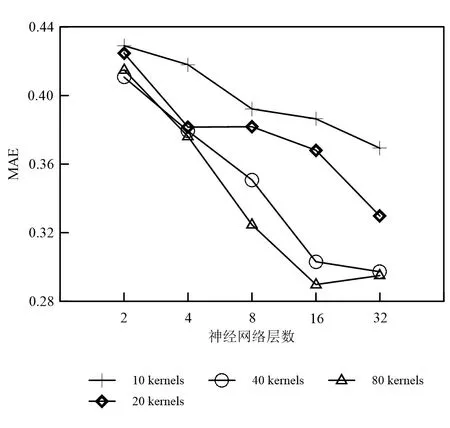
图5 卷积神经网络中网络层数与每层卷积核数目对网络性能的影响Fig.5 Influence of network layers and kernel numbers of each convolution on convolution neural network performance

由图5可知，卷积神经网络在近似模型电阻率与响应信号之间映射时，其准确度随着网络层数与卷积核数的增加而上升。最优的卷积神经网络层数为16，每层卷积核个数为80。图6展示了最优的卷积神经网络在测试集上的性能，卷积神经网络预测电阻率的准确度大致随着深度增加而降低。曲线没有严格的单调递增，这可能是由于训练集样本多样性不够高，网络的优化算法不完美等众多因素导致的神经网络算法不能达到理论上的最优。

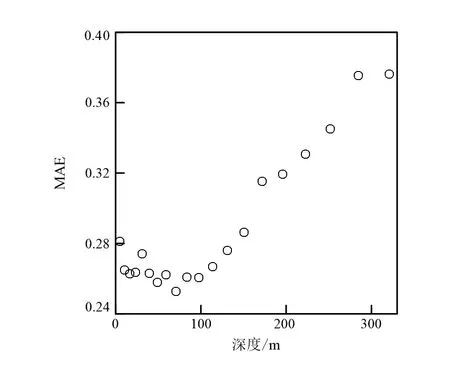
图6 卷积神经网络预测的电阻率与真实电阻率的平均绝对误差(MAE)随深度的变化趋势Fig.6 Changing trend of mean absolute error (MAE) calculated between true resistivity and predicted resistivity by convolution neural network with depth

1.3 循环神经网络

循环神经网络(recurrent neural network, RNN)针对时间序列进行建模，采用参数共享原则，且具有一定的记忆功能。最早提出的循环神经网络存在长期依赖问题，即其无法有效的利用历史信息,为了解决这个问题，Hochreiter et al.[18]提出长短期记忆模块。长短期记忆模块(long-short term memory, LSTM)通过其独有的‘门’结构，可以有效的解决长期依赖问题。

图7 LSTM模块的结构Fig.7 Structure of LSTM medol

长短记忆模块的基本结构如图7所示，xi表示t时刻网络的输入，hi表示t时刻网络的输出，si表示t时刻网络的隐含信息，W为连接不同‘门’的权重矩阵,b为‘门’的偏置矩阵。ff为遗忘门，其含义为从当前状态中丢弃的信息，ft=σ(Wfxxt+Wfhht-1+bf)，it与gt构成输入门，it=σ(Wixxt+Wihht-1+bi),gt=tanh(Wgxxt+Wghht-1+bg),ot所在的位置为输出门，ot=σ(Woxxt+Wohht-1+bo)。由此可得，st=gt·it+st-1·ft,ht=st·ot。循环神经网络与包含20个神经元的全连接层相连，从而预测20个不同深度的电阻率，循环神经网络的时间步长，即t的最大值设为4。使用测试集测试网络层数和LSTM的隐层神经元数目对网络性能的影响，实验结果如图8所示。

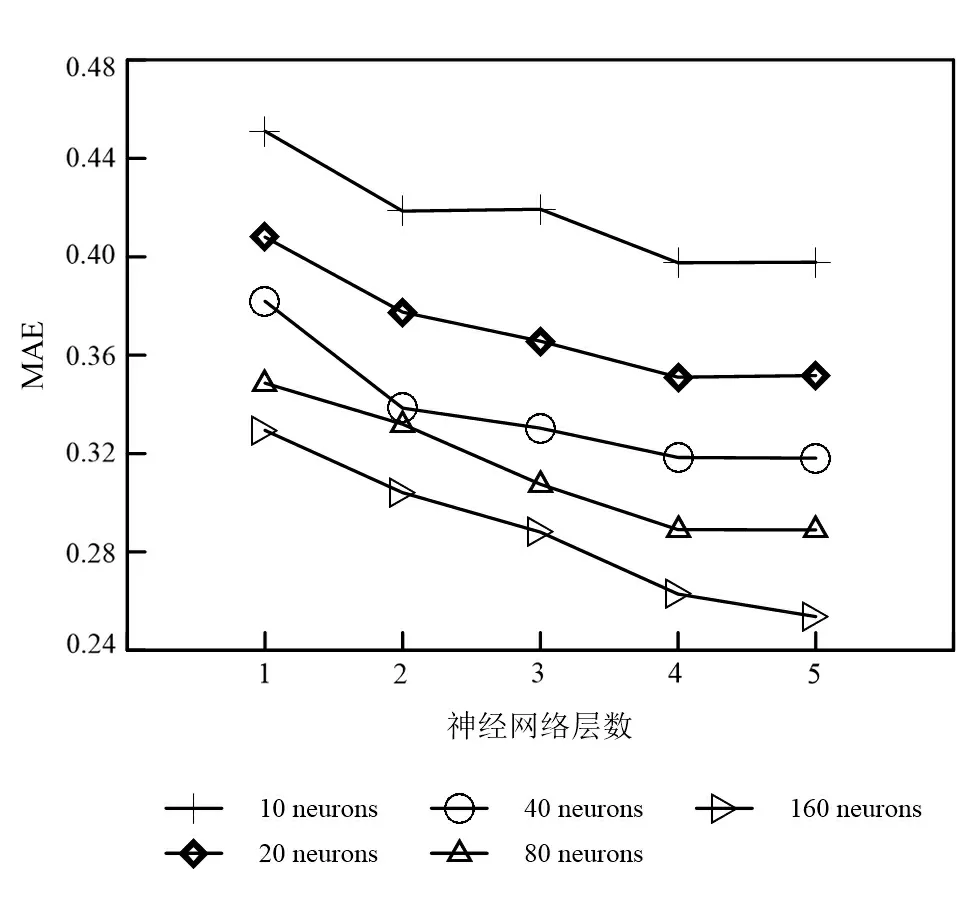
图8 循环神经网络中网络层数与隐层神经元数目对网络性能的影响Fig.8 Influence of network layers and hidden neurons number of recurrent neural network on network performance

由图8可知，循环神经网络预测电阻率的准确度随着神经网络层数的增加而升高，随着隐层神经元数目的增加而升高。在本实验中最优的循环神经网络为5层，隐层神经元个数为160。图9展示了最优的循环神经网络在测试集上的性能。

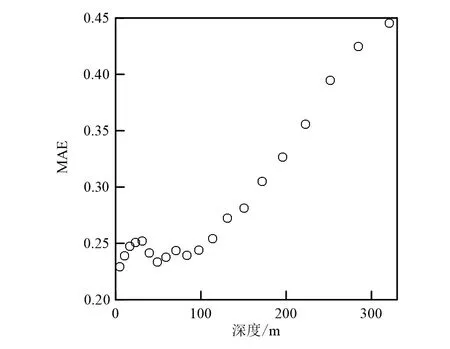
图9 循环神经网络预测电阻率值的准确度随深度的变化趋势Fig.9 Changing trend of predicted resistivity accuracy by recurrent neural network with depth

循环神经网络的记忆功能使得网络在预测深部电阻率时考虑浅部的电阻率信息，这使得所有时间道的数据都可以被有效的利用，增加了网络信息利用效率。另一方面，使用多层LSTM模块时，最后一层LSTM模块的输入可以看作是信号经过其他LSTM模块的预处理后得到的。考虑LSTM模块在时间方向的训练速度慢，认为在保留最后一层LSTM的前提下，建立不同的神经网络组合系统也会得到较好的效果。

1.4 混合神经网络系统

构建了包含两种神经网络的混合系统，并通过实验测试两种神经网络系统在测试集上的性能。首先对全连接网络与LSTM组合的神经网络系统进行测试，网络层数采用4层，隐层神经元数为200，LSTM模块采用40个神经元。图10展示了该神经网络系统在测试集上的性能。

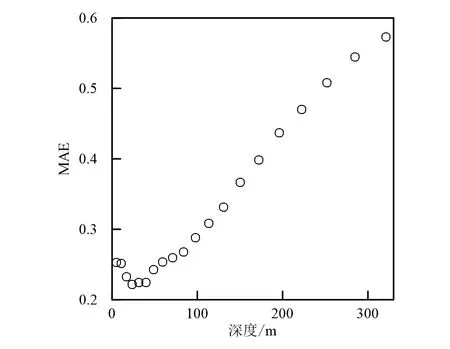
图10 全连接网络与LSTM网络结合预测电阻率值的准确度随深度的变化趋势Fig.10 Changing trend of predicted resistivity accuracy combined by full connected network and LSTM network with depth

考虑到卷积神经网络的工作方式符合电磁信号的数据特征的先验信息，建立了CNN与LSTM相结合的神经网络系统，即电磁信号首先被输入到3层卷积神经网络中进行特征提取，再通过单层LSTM模块中输出地下模型。卷积神经网络每层的卷积核数为40， LSTM模块采用40个神经元。图11为该神经网络系统在测试集上的表现。

图11 卷积神经网络与LSTM网络结合预测电阻率值的准确度随深度的变化趋势 Fig.11 Changing trend of predicted resistivity accuracy combined by convolutional neural network and LSTM network with depth

2 网络性能对比

神经网络具有很强的近似函数能力，一个包含足够多参数的三层神经网络可以逼近任意连续函数。然而，训练这样的网络是不现实的，因为其不仅要求指数倍增长的参数数量，且目前为止没有合适的优化算法。实际上，在使用神经网络建模时，合理的网络结构往往能达到事倍功半的效果。网络结构确定了某个泛函空间，在一个合理的泛函空间进行函数搜索会加快网络收敛速度，降低网络参数数目。另外，较少的参数会使得网络不易过拟合，具有更强的泛化能力。为了找到合理的网络模型，测试了不同类型的神经网络的性能，且采用在测试集上表现最优的网络结构进行对比分析，并统计了不同种类的神经网络训练所用时间(表1)。

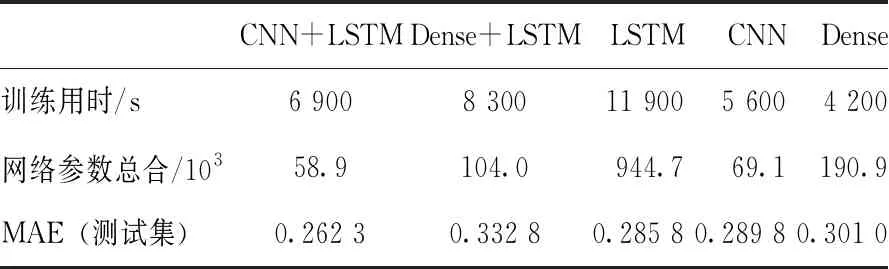
表1 神经网络性能对比分析

表1直观的表明了CNN与LSTM的组合与其他网络组合相比，性能最好，使用参数数量最少，这在一定程度上证明了该组合更适合用来近似电磁信号与地下模型之间的映射关系。

3 理论数据成像

通过分析得知，CNN与LSTM相结合的网络结构更适合近似电磁信号与地下模型之间的映射关系，图12为不同神经网络在处理理论数据上性能的差异。

由图12可知CNN与LSTM网络在处理理论数据中的优势。为了测试CNN与LSTM相结合的神经网络处理实测数据的潜能，构建了加有不同程度高斯噪声的测试集，测试结果如图13所示。

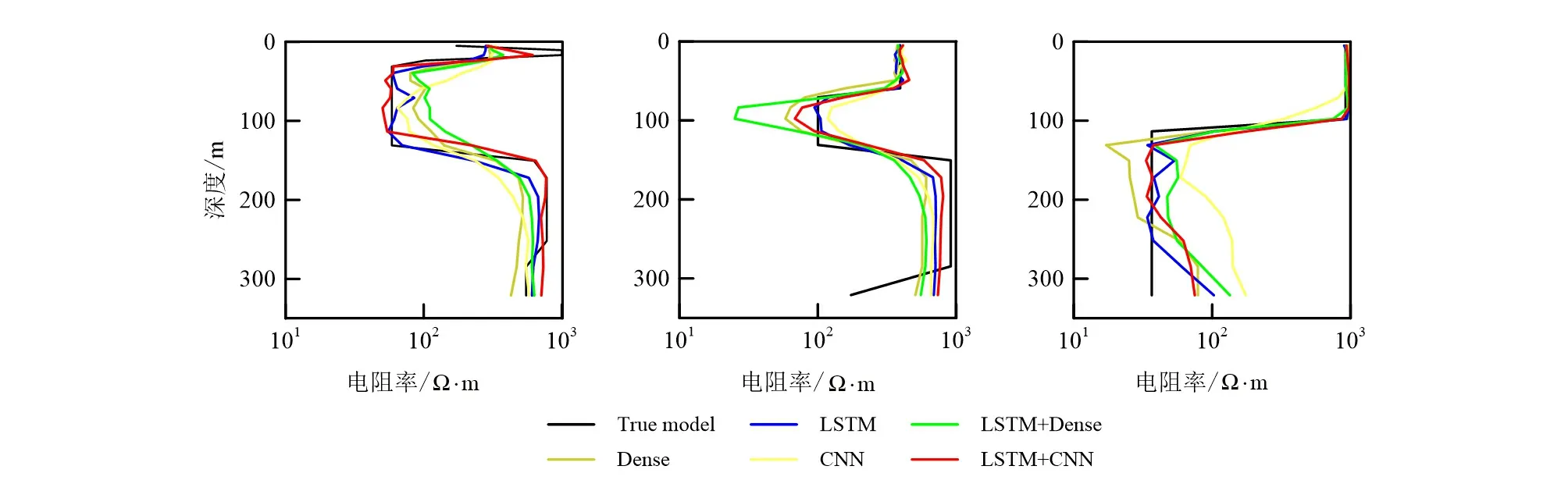
图12 不同种类神经网络在测试集(3个随机算例)上的表现Fig.12 Performance of different neural networks on test set

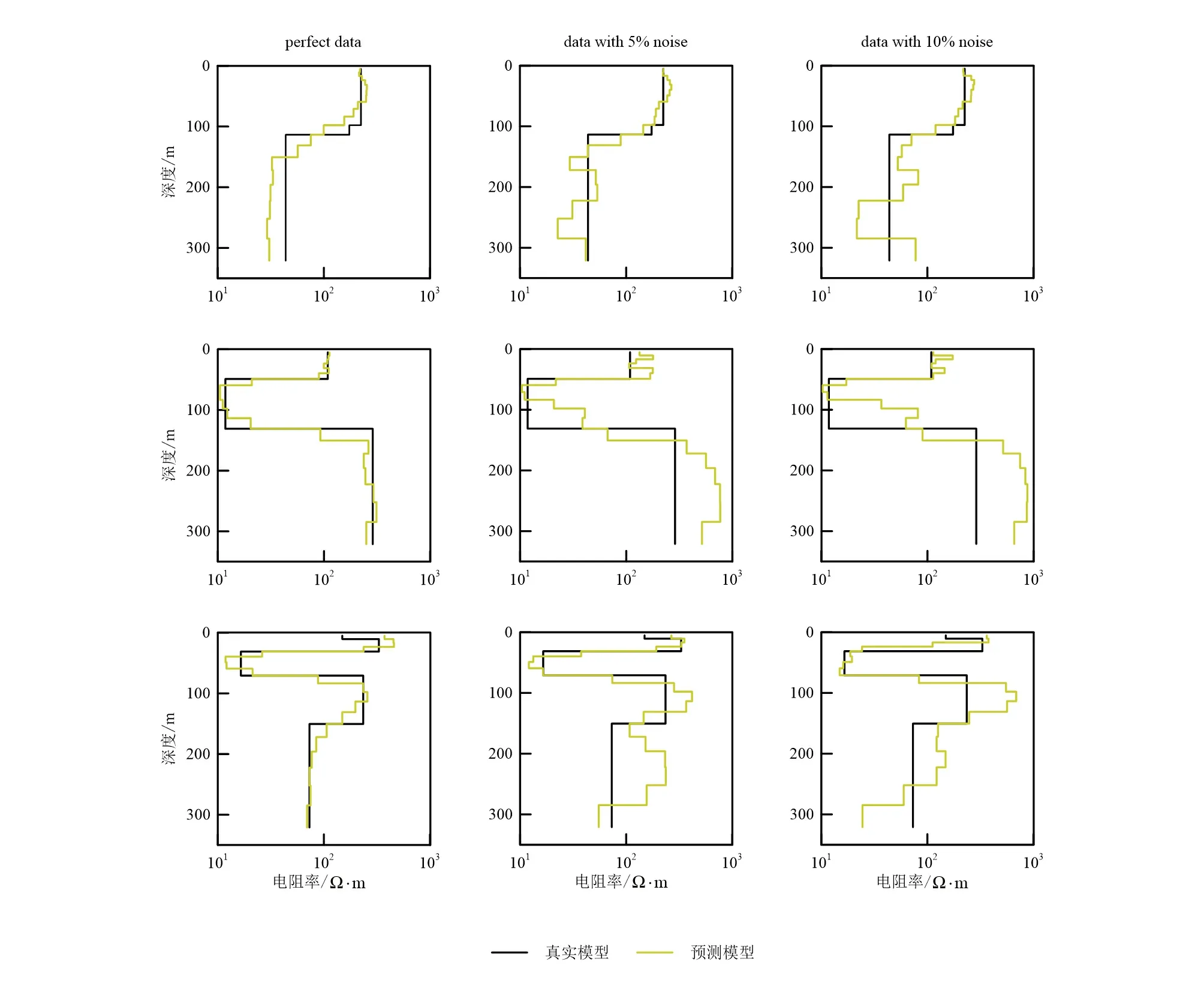
图13 神经网络系统(CNN+LSTM)在测试集上的表现Fig.13 Performance of neural network system (CNN+LSTM) on test set

由于采用提前停止训练的方法,网络会获得一定的抗噪能力。通过图13可以发现在10%的高斯噪声影响下，神经网络预测的模型依然可以较好地反映真实模型信息，这说明该方法有一定的抗噪能力，有潜力处理实测数据。

4 结论

(1)通过数值实验与网络模型测试，CNN与LSTM结合的神经网络设计综合考虑了电磁信号的结构，获得电磁信号的物理过程，更适合用来近似电磁信号与地下模型之间的映射关系。

(2)通过早停法训练的CNN与LSTM结合的神经网络有较强的抗噪能力，能用来处理质量参差不齐的数据，为实测数据处理提供理论依据与方法基础。