基于神经网络的大连东北海岸带碎石土地基强夯加固研究

邓浩，张延军，单坤，倪金，岳高凡

1.吉林大学 建设工程学院, 长春 130026； 2.中国地质调查局 沈阳地质调查中心, 沈阳 110000； 3.中国地质科学院 水文地质环境地质研究所, 石家庄 050060

0 引言

近年来中国经济发展迅速，城市建设步伐日益加快，市区内可用的建筑用地愈加紧张，在海边建造各种设施是人类拓展活动空间的有效方法。部分山地多平地少的沿海地区选择采用工程爆破或者机械开挖形成的开山土石运至海岸带上作为地基，从而形成碎石土地基。碎石土地基在大连市较为常见，在国内外亦有广泛应用，其形成环境与工程实施密切相关，工程碎石土的主要特点在于其颗粒不均匀、分选困难、级配变异性大，密度代表值难以确定；且固结度较低，孔隙较大[1]。故相对于其他地基处理方法，强夯法对于碎石土地基更为合适。

由于碎石土自身的复杂性以及人为因素的影响，造成测试其物理力学性质参数困难，而解决这一难题的最有效方法之一就是反分析方法。目前，岩土工程反分析可分为应力反分析法、位移反分析法和应力与位移的混合反分析法[2]。用位移数据测量简便且精度较高，而位移又与岩土体的内摩擦角、内聚力和泊松比等参数关联紧密，因此，位移反分析法目前应用最为广泛。人工神经网络参数反演分析，是以工程类比法为背景，通过神经网络位移反分析得到岩土体相关参数的方法。人工神经网络已应用于许多岩土工程问题，并取得了一定的成功[2]。Ranasinghe R A T M应用神经网络程序设计以动态圆锥贯入仪试验结果预测滚动强夯效果[2]；Kumar V的研究将人工神经网络应用于混合地基和加固地基，并进行了比较，了解神经网络模型在不同基础系统中的不同表现[3]；Omar M 提出利用人工神经网络预测阿拉伯联合酋长国沙迦浅层颗粒土的容许承载力和弹性沉降[4]；Alzo’ubi A K采用人工神经网络方法建立了能够预测桩身静载试验结果的模型[5]；Rahimi E采用神经网络对伊朗西南部的Bakhtiari和Karun 4个坝址的岩土参数受水泥的影响进行了估算[6]；余方威应用神经网络进行了岩质边坡的位移反分析[7]；边睿曾应用BP 神经网络进行隧道位移反分析研究[8]；周志广应用BP神经网络进行沈阳地铁开挖引发地面沉降的反分析[9]；周瑜等人应用神经网络研究了岩土体的细观力学参数[10]。

BP神经网络模型目前在碎石土地基的应用较少，其自身所具有的特殊性，可以在反演计算的过程中不再考虑力学作用的原理，应用其强大的函数非线性运算能力，结合已有的样本进行学习，就可以通过反演获得岩土体的相关参数[11]。相比于原位测试与室内试验，得出的结果方便快捷，也真实可靠。

本文针对flac3d强夯模拟程序中应用于计算的几个力学参数与所对应的沉降量，应用BP神经网络模型所建立的映射关系，进行以沉降量为已知量的力学参数反分析，计算所得土层力学参数可应用于进一步的工程建设。

1 BP神经网络计算模型

1.1 神经网络模型基本原理

人工神经网络无需事先确定输入输出之间映射关系的数学方程，仅通过自身的训练，学习某种规则，在给定输入值时得到最接近期望输出值的结果。作为一种智能信息处理系统，人工神经网络实现其功能的核心是算法。BP神经网络是一种按误差反向传播训练的多层前馈网络，其算法称为BP算法，BP 网络学习算法的基本原理是梯度最速下降法，中心思想是调整权值使网络总误差最小。其网络结构模型包含输入层、隐含层和输出层 3 个层次。

图1 BP网络学习原理Fig.1 BP principles of network learning

此算法包括信息正向传播和误差反向传播两个过程，3 个结构层次的神经元分别负责信息和数控的输入，处理变换和输出处理结果[12]。

图1所示的是一个三层10个神经元的神经网络系统。其工作原理:

设输入向量为：

Akn=(a1n,a2n, …，ann)

(k=1,2,3,…,m;n=1,2,3,…,N)

式中：m为学习模式对数目；N为输入层神经元个数。

对应输入模式的希望输出向量Yk=(y1,y2,…，yp)，即输出层神经元个数，中间层各单位单元的输入按下式计算：

(1)

式中：Wij为输入层至中间层的连接权；θj为中间层神经元的阈值；p为中间层神经元的个数。

为模拟生物神经元的非线性特性，以Si作为S型函数(Sigmoid函数)的自变量，计算中间层各神经元的输出，S型函数取：

(2)

式中：f(x)称为激励函数。而中间层神经元激活值为：

bj=f(xj) (j=1,2,…,q)

(3)

信息从输入层流向输出层，给定输入信息，便得到相应的输出结果，即：

(4)

式中：Lt为输出层各单位单元的输入值；Ct为网络的输出值。

可见存在一个三层网络能够以任意精度体现任意连续函数的映射[13]，但是想构建起这种映射，需要对神经网络模型进行样本训练。

1.2 神经网络模型的建立

BP神经网络模型的计算精度、速度等性质决定于其结构层的参数，故建模的首要任务是合理的确定神经网络模型的机构层参数。本次训练的模型中将隐含层层数设置为1，隐含层节点数设置为12。最大训练次数为5 000，学习率为0.001，训练要求精度为0.000 01。故以实际夯沉量作为输入层参数。本文数值模拟应用flac3d，进行强夯处理时应用的主要力学参数为内聚力、内摩擦角、弹性模量和重度，本文应用此4个参数作为输出层参数。

文中训练样本的参数依照已有的重庆地区工程数据[14]，该工程中的碎石土成分与级配等与本文所选研究场地相近，所含碎石成分主要为灰岩，选取其中的典型值进行计算，并结合规范中的经验值，每种参数选出4组数据。本文采取正交试验方法，对所选参数进行组合，每组参数对应的沉降量用数值模拟软件求得，应用flac3d软件进行计算的主要参数包括弹性模量E、内摩擦角Φ、内聚力C和土层的重度γ，获得最后的训练样本(表1)。

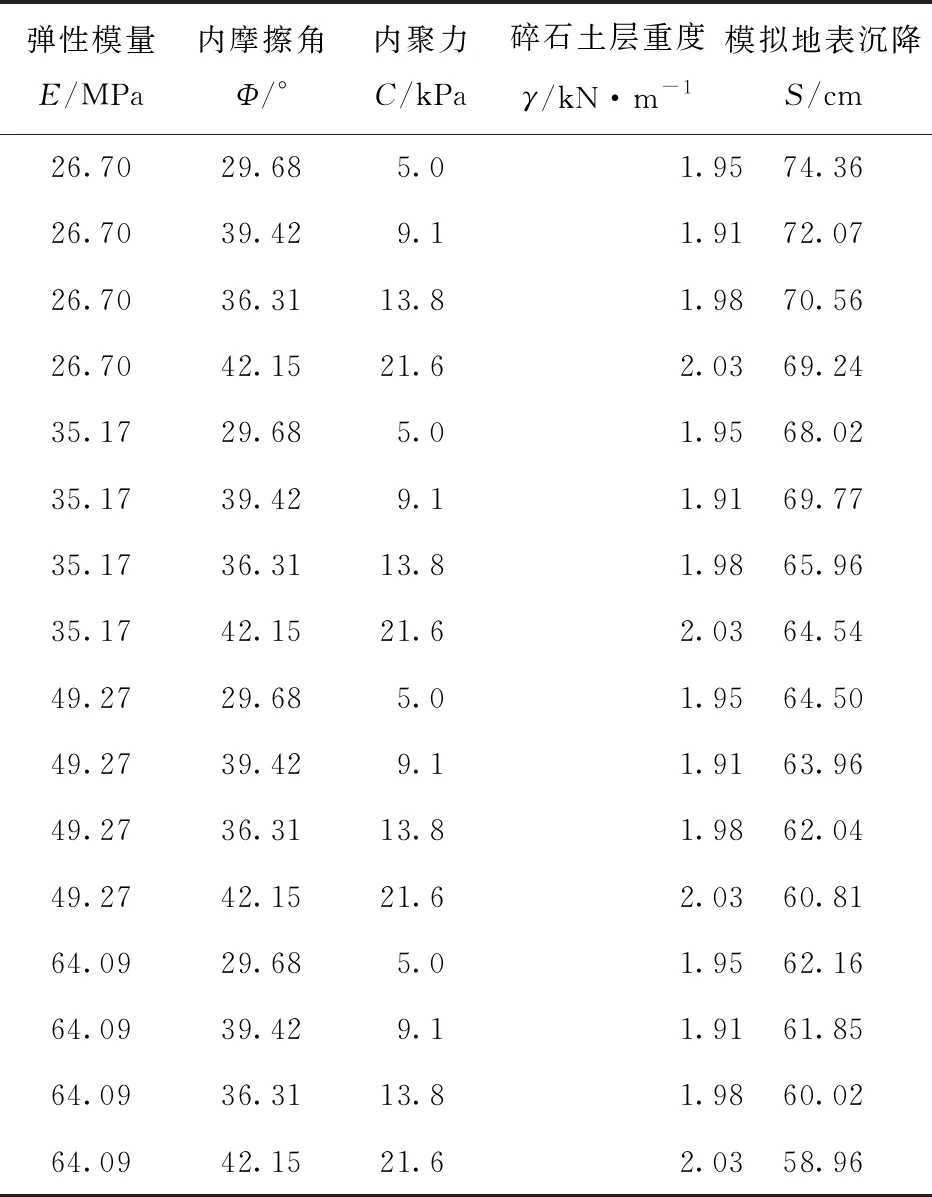
表1 训练样本信息表

2 工程实例

2.1 工程概况

本工程位于大连市，填海造陆形成，回填材料均为开山土石，回填层厚度约为3～10 m，土体渗透能力强，场区与海水连通，受潮汐影响明显。第一步按照施工图要求，施工场地先回填至夯前标高，然后分区进行分不同夯击能的强夯处理。试验区地基处理方法为：一遍1 000 kN·m 点夯，夯后推平工作面再进行1 000 kN·m 满夯，夯后推平工作面碾压，如此程序进行并逐次提高夯击能。仅计算1 000 kN·m点夯的情况，此时点夯的沉降量为54 cm。

2.2 地质条件

本场地回填全部采用陆填方案，开山碎石土由陆上直接进行回填，回填材料为开山碎石土，碎石含量>50%，一般粒径为20～200 mm，最大粒径不超过300 mm，集配均匀。

淤泥质粉质黏土第四系全新世海相冲积层。灰褐色，饱和，流塑--软塑，有腥臭味，层厚1.6～3 m，层底标高-8.96～-4.49 m。

含碎石粉质黏土第四系更新统洪积层。黄褐色，可塑，稍湿，分布于部分场地，层厚1.10～3.70 m，层底高程-12.39～3.28 m。

板岩该地层分布于整个场地，地质时代为青白口系桥头组二段。灰褐色，岩性为板岩夹石灰岩。各个土层参数见表2。

表2 地层力学参数表

2.2 参数反演

按照2.1节的设定进行神经网络模型的训练，训练性能图如图2所示。

图2 神经网络模型训练性能图Fig.2 Training performance diagram of neural network model

训练完毕以后在软件中输入工程的实测沉降量54 cm，经BP神经网络模型反演获得参数见表3。

表3 反演计算结果

2.3 反演参数的验算

将神经网络模型反演所得岩土力学参数作为已知条件，应用flac3d软件进行计算，再用计算所得强夯沉降量与实测沉降量进行对比分析。

2.3.1 强夯模型的建立

按照常规计算确定地基处理影响深度<12 m，水平影响范围<5 m，碎石层以下模型网格划分为30 m×30 m×20 m，碎石层以下总网格量为27 000块。试验区地基处理模型网格划分(图3)。

图3 强夯模型网格划分图Fig.3 Mesh division diagram of dynamic compaction model

2.3.2 强夯模型的模拟结果的误差分析

应用反演获得参数建立数值模型后，经计算获得沉降曲线如图4所示。沉降量结果为56.63 cm，相比于输入的实测沉降量54 cm，误差为4.87%，其精度可以满足工程控制要求。

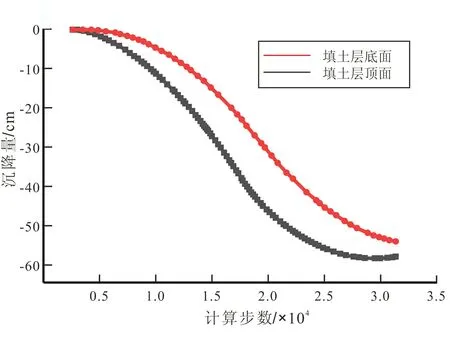
图4 沉降曲线Fig.4 Settlement curves

3 讨论

以数值模拟方法作为主要研究手段，同时应

用了正交试验设计。在合理设置神经网络模型的结构参数情况下，基于碎石土的位移反分析方法对碎石土的力学参数进行了分析研究，将反分析得到的结果输入数值模拟的正分析程序，从而验证神经网络反分析方法的准确性与可行性。

BP神经网络相比于其他位移反分析模型具有自适应、自学习的特点，文中以16组数据作为训练样本，即可获得较为准确的数据，可见其可以适应实际工程面临的动态条件的变化。

若能结合区域内同种工程的勘察设计资料，应用已有的成果作为参考，通过计算机算法与地质勘察手段相互结合，可以省时省力，倘若训练样本的数据量足够多，所得数据会亦更加准确可用。对于土层的变形沉降的预测以及稳定性评价有重要意义。

以传统的手段获得碎石土的力学参数，要通过室内试验，而碎石土无法取得原状土样，这就意味着需要进行土样的重塑，以及考虑土样密度与级配等因素的影响，过程复杂且不确定因素较多。相比于室内试验，神经网络模型的反演分析方便且迅速。

笔者模拟采用flac3d软件，土体应用 Mohr--Coulomb弹塑性模型，如果选择其他软件或者其他模型，所涉及参数会有变化，但是此法亦可应用。

4 结论

(1)基于神经网络反演获得地基土力学参数的方法可行，此方法能省去繁琐的室内试验过程，极大地节约了人力物力。

(2)神经网络模型反演所得试验参数以flac3d数值模拟进行计算，求得沉降量为56.63 cm，现场实测值为54 cm，误差为4.87%，误差在可接受范围内，证明了以BP神经网络进行位移反分析方法的所得结果较为准确可信。

(3)样本数据仍然需要进行室内试验与原位测试才能得到，故此法的适用基于对目标工程周边相似条件的工程资料的掌握。