基于混合聚类的岩体结构面优势分组方法

许扬，张文，符锐，聂振邦，兰志广，陈怀玉，单博

1.吉林大学 建设工程学院，长春 130026；2.中国电力工程顾问集团 东北电力设计院有限公司，长春 130026

0 引言

岩体由岩块和结构面组成，岩体的力学、变形与水力性质均受到结构面的控制，在岩体工程的众多方面，如地质分类、岩体边坡稳定性分析计算等，结构面产状是必须考虑的基础性参数。获得岩体结构面的特征及其组合分布规律，是进行岩体工程稳定性分析评价的基础。

岩体结构面的发育是有规律的。结构面产状表示方法通常采用玫瑰花图、极点图等。传统的结构面分组方法借助这些图来进行人工分组，该法分组简单直观易操作，但面对结构面数据多且复杂时，难以得到准确统一的界定结果。由于计算机科学的进步，聚类分析法在结构面优势分组的运用得到普遍关注。聚类分析是一种将研究对象分为相对同质群组的统计分析技术。许多国内外学者运用聚类算法进行结构面分组，Shanley et al.[1]首次将数学方法应用于岩体结构面分组的研究，该法主要通过确定不同的搜索半径以寻找密度点来进行结构面聚类；陈剑平[2]在Shanley的方法基础上用右手法则来表示结构面产状，该法可以更简洁地表示结构面的几何特征；周玉新[3]分析了模糊等价聚类方法和模糊软划分聚类方法的优缺点，将两种方法相结合对岩体结构面进行分组；张奇[4]提出基于凝聚层次聚类方法的岩体结构面产状优势组划分法，该法简单快速不需要确定初始中心，但常会遇到选择合并点的问题，一组对象被合并成一类便不能撤消，若选择不合适,会出现不理想的分组结果；Harrison et al.[5]首次将模糊C均值算法(FCM)引入到岩体结构面优势组划分中；冯羽[6]提出一种将结构面产状图形分析法、模糊等价聚类方法和FCM法有机结合的结构面产状分类综合性方法。由于FCM算法相对于其他聚类方法具有良好的普适性且较易实现，使它在岩体结构面分组中得到广泛应用。但FCM算法其本质上是一种局部搜索寻优法，易陷入局部极小点，它对初始中心点的选择较为敏感。对于FCM法的缺陷，宋金龙等[7]、宋盛渊等[8]都提出了优化中心的改进方案。

岩体结构面优势分组理论日益发展，但现有方法仍存在一些问题。一方面，聚类算法易受初始中心的影响，人工给出初始中心对分组结果影响很大，尽管一些学者用智能算法对初始中心优选，但这些算法的控制参数较多且实现复杂。另一方面，如何剔除结构面产状中的孤值也是要考虑的问题。为了解决上述问题，笔者提出一种基于混合聚类的结构面产状分组方法，利用凝聚层次聚类自动确定初始中心随后结合高计算精度的FCM法，把它们结合为混合聚类算法，并增加结构面产状中孤值产状分析，能有效剔除结构面数据集中的噪声点。通过对人工生成产状数据分组检验了该法的正确性，并应用到大藤峡水电站泄水闸坝基岩体分析中，得到了较好的分组结果。

1 工程地质条件和数据采集

大藤峡水利枢纽主坝位于珠江流域西江干流黔江河段的大藤峡出口弩滩附近，距桂平黔江彩虹桥6.6 km，是黔江梯级规划中最末一个梯级。大藤峡水利枢纽周边地区的地形总趋势是西北部高，东南部低平，其中大藤峡峡谷出口段长约2 km，是从上游大瑶山区低山地带过渡到下游桂平盆地的丘陵地带，右岸山势较高。大藤峡水利枢纽地理位置图如图1所示。

图1 大藤峡水利枢纽地理位置Fig.1 Geographical location of Datengxia water control project

大藤峡水利枢纽泄水闸坝段位于左岸漫滩，地形起伏较大，地面高程23～43 m。泄水闸坝基底地层主要为郁江阶D1y1--1层至D1y1--3层，岩性以细砂岩、含泥细砂岩、泥质粉砂岩、泥岩及灰岩为主，并发育大量与层面产状一致的泥化软弱夹层。坝基岩体中发育有较多陡倾断层，降低了岩体的整体性。为保证工程安全性，需要对泄水闸坝基岩体进行研究。

在郁江阶各地层中，D1y1--3地层结构面发育，岩体完整性较差，且该地层距坝轴线较近，结构面发育情况对坝基工程建设的影响相对较大。因此，本文选定D1y1--3地层的岩体裂隙进行岩体结构面优势分组研究。D1y1--3地层属于泥盆系下统郁江阶下段，岩性主要为灰--灰黑色灰岩、白云质灰岩。层面发育，岩层厚度一般为15～30 cm，呈层状。岩层产状约为倾向10°～20°，倾角60°～90°。运用取样窗口法对郁江阶D1y1--3层岩体结构面进行测量，得到了该地层共276条结构面的产状方位数据并根据实测产状绘制结构面产状极点图(图2)。

图2 D1y1--3地层岩体结构面极点图Fig.2 Pole of D1y1--3 strata rock mass discontinuity

2 结构面优势分组方法

2.1 结构面产状的空间表达

假设结构面为一空间平面，结构面的产状可用它对应的单位法向量来表示，建立空间直角坐标系如图3所示：即x，y和z轴分别指向正北、正东和正上方。结构面产状的上下半球单位法向量坐标即可表示为P=(x,yz)和P′=(x′,y′,z′)。其中：

x=cosα·sinβ

(1)

y=sinα·cosβ

(2)

z=cosβ

(3)

x′=-cosα·sinβ

(4)

y′=-sinα·cosβ

(5)

z′=-cosβ

(6)

式中：α为倾向；β为倾角。

图3 结构面产状的表达Fig.3 Representation of discontinuity occurrence

2.2 分析结构面数据中的孤值点

大量结构面产状的实测结果中往往有一些结构面产状与其他产状都存在着较大的偏离，使结构面产状数据中存在孤值点。而聚类方法对孤值点极为敏感，有时甚至会对整体的聚类效果产生巨大影响[4]，因此需剔除孤值点。

孤值点产状有两个特征：①并非大量的密集的存在，因此在总体中占比较小；②孤值点产状与其他产状均有着明显的区别。所以，可利用极点图对孤值点筛选。本文令极点图的半径为1 cm，并以圆心为原点，将结构面产状按关系式(7)投入到上述极点图中；绘制各极点与其他极点距离最小值关系图辅助判断(图4a)，其中两极点间距离D的计算为式(8)，并将其最小值记为Dmin。设定距离阈值R，并将Dmin值大于R的全部剔除。此外，将孤值点数据占比p值做出限定。一般来讲，剔除原数据集总量的5%可在保持数据集整体信息完整的同时使数据更加紧凑[9]，所以将p值设定为0.05。由公式(9)可得数据的最大剔除量N，式中M为数据集的数据个数。综上，满足公式(10)的极点即判为孤值点。

(7)

(8)

N=p*M

(9)

(10)

2.3 混合聚类算法的介绍

岩体结构面优势分组是对产状相近的结构面归类，而聚类算法以相似性度量准则判定两结构面是否相似。结构面产状越相近，极点在球面上的距离也就越小。基于本文表征结构面的方式，可使用欧式距离作为结构面间的相似性度量准则。欧式距离公式如式(11)所示,其中d表示两极点p1(x1,y1,z1)和p2(x2,y2,z2)间的距离。

(11)

混合聚类算法中应用了凝聚层次法和FCM法。凝聚层次法将每一个结构面极点作为一组聚类。通过欧式距离的计算，得到每一个极点与其他极点之间的距离，找到距离最短的两个极点，把他们聚为一组。然后计算剩余组聚类的距离，仍然将距离最小的两组合并为一组并往复如此，当聚类数达到设定的组数时为止。FCM聚类算法令X={X1,X2,…,XN}⊂R，其中N为样本数据子集个数，R为三维实数空间R3中的一个有限样本。将结构面产状样本集分为C类，C为聚类中心数，则矩阵的U=[uik]便是X的一个模糊C划分，uik即为Xk对第i个类的隶属度。定义聚类目标函数为：

(12)

(13)

(14)

式中:V为C个聚类中心组成的集合V=[vi]；d为采用的相似度度量公式；m是加权指数，m值越大则分类越模糊，实际应用中m值一般取2。当聚类准则取最小值即min{Jm(U,V)}时，即为最佳分类结果。通过式(13)和式(14)进行迭代计算直到式(12)小于给定的阈值，此时即完成聚类。

通过将两种算法结合为混合聚类法后，便可设定不同结构面分组数进行划分。但不同的分组数会得到不同的分组结果，本文使用聚类有效指标XB值来确定最佳分组数。

2.4 聚类结果的检验

1991年，Xie et al.从数据集的几何结构出发提出了Xie--Beni有效性指标，该指标同时考虑了几何结构和隶属度，评价聚类划分质量全面并广为应用，其具体表达式为[10]：

(15)

式中：U为隶属矩阵；V为聚类中心矩阵；C为聚类数；m为模糊因子；uij为U矩阵中的元素；vi为V矩阵中的第i行元素。组内的数据越密集，组与组间距离越大，XB值就越小，聚类效果也就越好。本文使用Xie--Beni有效性指标来评价聚类结果的好坏，进而确定最佳分组数。每次分组后计算XB值，该值最小所对应的分组数C即为最佳分组数。

3 方法的可行性验证

为了验证新方法的分组正确性，对人工生成的产状样本进行优势分组，对比人工设置参数和新方法计算结果来检验新方法的可靠性。

3.1 人工产状样本数据的生成

许多研究者都认为结构面法线方向的概率密度函数符合Fisher分布[11--12]，即各优势组极点的分布符合Fisher分布。笔者运用Fisher分布来生成人工产状数据，Fisher函数生成极点的详细推导见文献[13]。

人工生成结构面产状前需要设定产状均值和聚合度K，其中聚合度是反映围绕在均值周围的样本的聚类程度。聚合度越大，围绕均值聚集程度越高。本文设定3个中心产状及聚合度生成模拟产状数据(表1)。为了模拟天然裂隙岩体中的随机裂隙，添加了NE42°∠67°、SE131°∠27°、NW335°∠45°和SW193°∠84°的孤值产状，根据Fisher函数和2.1节所述方法，生成了人工产状数据。

3.2 方法的检验

完成人工产状数据的生成后，运用混合聚类法进行分组：先判定并剔除数据集中的孤值点，绘制各极点与其他极点的最小距离图(图4a)。在图4中可见有4个极点与其他极点的最小距离值Dmin明显较大，其离差均>0.3，即对该数据集的距离阈值设定为0.3。人工产生结构面总数为224个，根据公式(9)和(10)中的关系判定该4个极点为孤值点，从数据集中剔除。之后，试算不同的分组数的XB指标值(表2)，可知分3组是该样本数据的最佳分组数(表1、图4b)。

根据分组结果可知，该方法成功地剔除4个孤值产状。由表1可知，层次聚类法得到的初始中心和设置中心非常接近，说明该法为FCM法提供了合适的初始中心产状。结合表1和图4可知，分组后每组的产状数量、平均产状都与样本的设置参数十分接近，说明该方法能提供准确可靠的结构面产状划分。

表1 设置参数与分组结果对比

Table 1 Comparison of parameters setting and grouping results

组号参数K数量/个倾向/°倾角/°设置值12040230.0°40.0°1初始值/1231.3°40.8°结果/40230.4°40.6°设置值8010095.0°80.0°2初始值/195.3°80.4°结果/10095.5°79.7°设置值11080160.0°85.0°3初始值/1158.4°84.4°结果/80159.9°83.4°

表2 不同分组数的XB指标值

a.各极点与其他极点间的最小距离；b.孤值点在极点图中的表示。图4 模拟数据中的孤值点Fig.4 Outliers in simulated data

4 实测结构面的优势分组及分析

为了进一步验证混合聚类方法在实际工程运用中的分组效果，分别用该法和FCM法对大藤峡坝址区D1y1--3地层实测岩体结构面产状数据进行优势分组。

用FCM法进行结构面产状优势组划分。该法将极点投影到单位球的上半球，用两结构面所夹锐角正弦的平方作为相似性度量，分组前需人为指定初始中心点，即需要人为确定结构面数据中有哪几个优势方位并给出优势方位的产状。通过D1y1--3地层岩体结构面极点图(图2)可以观察到图中灰色区域的极点分布相对密集，该区域的倾角大致为70°～85°，倾向大致在15°～35°至110°～150°之间。据此，设置了不同的初始优势产状(表3)。FCM法分组后的结果见表3和图5。

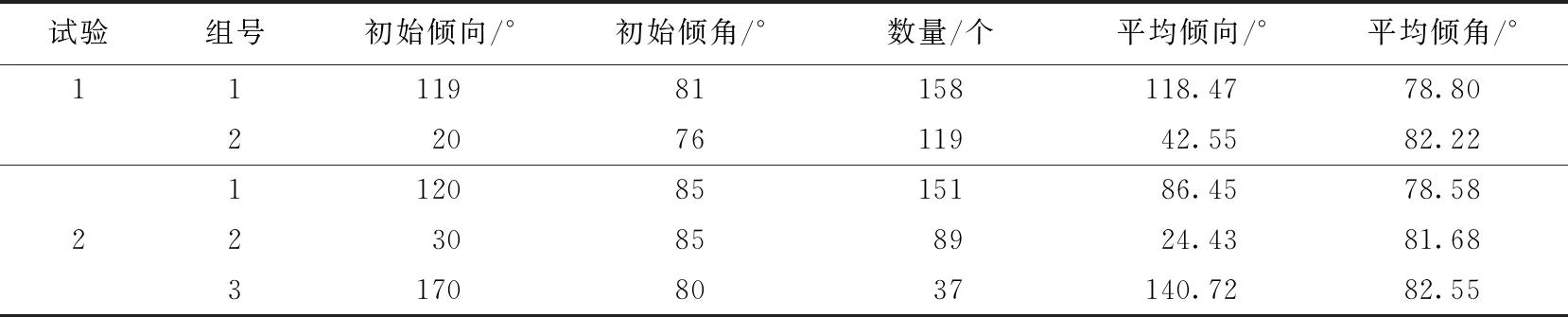
表3 FCM法参数设置及分组结果

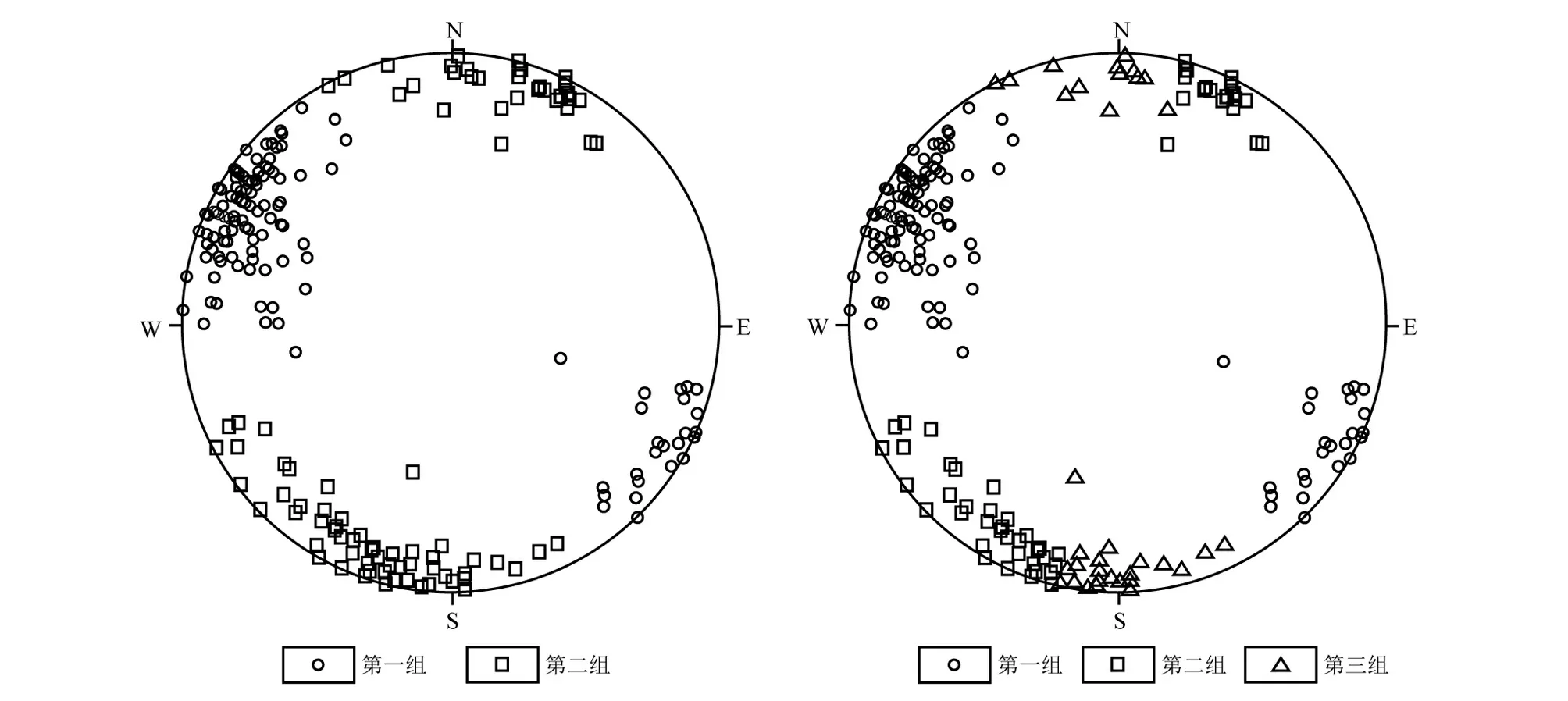
a.用FCM算法将极点分为2组；b.用FCM算法将极点分为3组。图5 FCM算法分组极点图Fig.5 Grouping pole of FCM algorithm

用本文方法进行岩体结构面产状优势分组。先进行孤值点分析，在图6a中编号42和226的极点距离值明显偏大，满足公式(10)，故设定距离阈值R=0.2将其剔除。试算对于不同分组数的XB指标值(表4)。 由试算结果可知在分2组时取得最佳聚类效果。因此将结构面划分为2组(表5)，分组后的极点图如图7所示。

表4 混合聚类算法计算各组的XB指标值

Table 4XBvalues in each group by hybrid clustering algorithm

分组数234567XB值0.0460.5030.4150.3650.3020.512

据图5a可知，利用FCM法可以有效地将结构面分为2组。组内极点大体距离较近，组间分离较好，但2个孤值极点并未剔除，分别并入第1组和第2组内。而这些极点的产状与其他组内成员都有着较大的差距，孤值点1的产状为110°∠38°，组内其他产状均值为118.83°∠78.96°。孤值点2的产状为16°∠54°，组内其他产状均值为41.25°∠82.46°。因此将它们与其他组内的极点归于一类并不合适。通过图5b可知，根据设置的3个初始中心点FCM法可以有效的将结构面分为3组。第1组和另外两组的界限比较明显，组内极点紧凑。第2组和第3组的边缘处紧凑，边界分离性差。从整体上分组结果比较合适，但在分3组的情形下第2组和第3组内仍存在与该组其他成员差别较大的孤值点，而且分组数和初始产状需依靠经验得出。

表5 混合聚类法参数设置及分组结果

Table 5 Parameter setting and grouping results of hybrid clustering algorithm

组号初始倾向/°初始倾角/°数量/个倾向/°倾角/°1118.6182.61156118.8078.99227.5888.9811841.2582.46

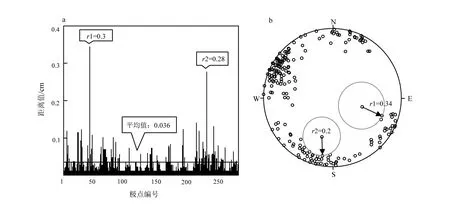
a.各极点与其他极点的最小距离；b.孤值点在极点图中的表示。图6 实测数据中的孤值点Fig.6 Outliers in measured data

图7 将极点分为两组Fig.7 Divides the poles into two groups

据图6所示，本文方法先进行孤值点搜寻并得到它们的产状分别为110°∠38°和16°∠54°。这些产状与其他产状的差别过大，故将这些孤值产状剔除。由表5可知，运用凝聚层次分析法得到的各组产状均值，即FCM法初始聚类中心和最终分组的各组产状均值相差不大，说明凝聚层次法提供了较好的前期划分。在分组结果中(图7)，各组组内极点紧凑，在两组边缘处的分离性较好，如在倾向135°和255°附近两组边缘都显示出了清晰的分离，综上可认为该分组结果较为理想。

对比两种方法的分组结果不难发现，传统FCM法有计算精确度上的优势，但它并不能区分孤值产状，而在面对分布形式复杂的产状数据时，人工确定初始中心产状及其个数也难以准确和统一。相比于此，本文方法一方面能够有效搜寻并剔除结构面数据中的孤值点，消除异常产状对结构面分组的影响，另一方面也减少了人为参与因素，能自动给出准确的初始中心产状，简化了操作过程并得到优良的结构面划分结果。

5 结论

(1)成功划分出人工模拟数据中添加的4个孤值产状。同时，凝聚层次法得到的初始中心与模拟数据的人工设定中心均非常相近。

(2)大藤峡D1y1--3地层结构面产状数据中存在2个孤值产状即110°∠38°和16°∠54°， 并在结构面优势分组前成功剔除。

(3)根据划分不同组数对应的XB指标值，将D1y1--3地层结构面划分为2组。第一组结构面共156条，平均产状为118.83°∠78.99°。第二组结构面共118条，平均产状为41.25°∠82.46°。