对仿猫跳跃机器人起跳过程中腰部作用的分析
陈贵亮,庄昌瑞,杨 冬,张笑颜,黄荣新,李铁军
(河北工业大学机械工程学院,天津 300130)
随着科技的发展,机器人逐渐代替人类在许多恶劣环境进行工作,如外星探索,军事侦察,火灾与地震救灾等。相比于传统的轮式和履带式机器人,腿式跳跃机器人因其良好的越障能力和对复杂环境的适应能力受到越来越多研究者的青睐。对腿式跳跃机器人的研究也是机器人新的发展方向。为推动腿足式机器人的应用与发展,美国国防先进项目研究所(DAPRA)于2012年设置了机器人挑战赛,以推动机器人在复杂不确定环境下完成复杂任务的技术研究[1-2]。在数亿年的生物进化中,生物在自然选择下进化出灵巧的运动机构和高效的运动模式,这也成为机器人发展取之不尽的灵感源泉。通过对仿生模本的研究可以得到仿生机器人的结构设计和控制原理的理论依据。近年来,许多高校和科研机构根据仿生原理,研制出了各种腿型仿生机器人。波士顿动力的big dog[3-4]可用于户外载重的任务,具有静态和动态的移动性能和完善的集成传感器系统;麻省理工学院的猎豹机器人[5-6]具备时速16 km/h的高速奔跑和跨越障碍物等功能;Plecnik 等[7]以夜猴为模本设计了一种高效的单足跳跃机构;以色列特拉维夫大学模仿沙漠蝗虫的半月板在跳跃中的作用,设计了在关节处利用扭簧蓄能的微小型跳跃机器人[8];西北工业大学的葛文杰等[9]对仿袋鼠机器人进行了研究;哈尔滨工业大学任毅豪[10]研制了仿青蛙机器人并对其进行逐步的改进;南京航天航空大学的王寰[11]利用对蝗虫的研究设计出一款能稳定跳跃的仿蝗虫跳跃机器人。
家猫作为一种善跳动物,跳跃能力高效稳定,且在生活中便于观察到,是良好的仿生模本。家猫的起跳过程对其最终的跳跃结果起着重要的影响,在家猫的起跳过程中,家猫的腰部中有着明显的姿态变化,因此研究家猫腰部在起跳过程中的作用对提高仿猫机器人的跳跃能力有着指导作用。
基于此,建立一个简单的仿猫跳跃机器人,根据家猫实际跳跃规律对其进行跳跃仿真,对仿猫跳跃机器人的简化机构进行动力学和运动学分析,验证其腰部在起跳过程中起到的作用;从能量角度比较有无腰部辅助跳跃的差别。研究结果可以对以后跳跃机器人的改进和控制提供参考。
1 家猫跳跃规律及运动分析
1.1 家猫跳跃观察实验
引导一只家猫进行跳跃实验。实验中诱导家猫越过障碍物,通过障碍物的长度反映家猫的跳跃能力。跳跃过程拍摄后,利用视频剪辑软件对主要跳跃过程进行截取以分析其运动规律,如图1所示。对几组跳跃实验中,家猫起跳瞬间各关节角度测量如表1所示。

图1 家猫跳跃实验截图Fig.1 A screenshot of a cat jumping experiment
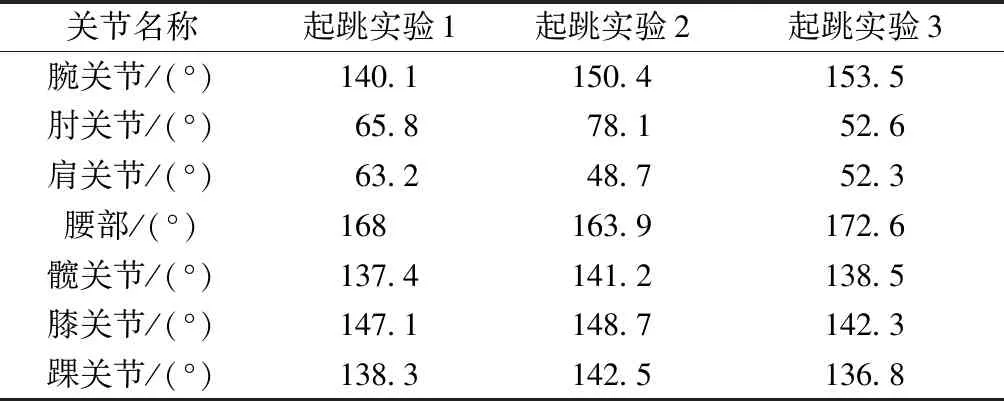
表1 起跳瞬间家猫各关节角度Table 1 Joint angles of cat at the moment of take-off
1.2 家猫跳跃运动分析
通过对几个跳跃过程的分析可得出家猫跳跃的一般规律。在起跳的预备阶段,家猫身体蜷缩,腰部拱起,整个身体成蓄能姿态;起跳时前腿先离地,身体向前舒张,腰部伸展同时后腿发力蹬地为跳跃提供动能;在空中通过姿态调整控制落点;落地时前脚先着地,通过腿部关节和腰部的弯曲消耗触地时的动能达到平稳落地的目的。在家猫起跳过程中腰部有着明显的收缩和伸展。为更进一步研究家猫腰部在起跳过程中的作用,需要进行起跳时与腰部有关的进一步分析。
2 仿猫机器人机构模型简化
由于家猫生物模本很难实现比较精确的指定参数的跳跃实验,且生物学参数难以测量,因此根据家猫骨骼模型(图2)设计了一个简单的仿猫跳跃机器人,机器人各部分长度根据猫骨骼模型测量比例进行分配(图3),用于对家猫的跳跃进行研究。如图2所示,家猫主要可分为前肢、躯干、后肢三个部分。前肢含有肩关节、肘关节、腕关节,后肢含有髋关节、膝关节、踝关节。前肢和后肢都可看作三杆机构,各杆绕各自连接关节转动,各关节均有扭簧提供弹性势能。由于不研究后脚掌在起跳过程中作用,所以柔性后脚掌可看作刚性杆。虽然家猫柔性脊柱由多个脊柱块组成,但最大转动发生在腰部,为了简化机构,将脊柱看作一二杆机构,在腰部由一铰链连接,简化后可得到一个八杆串联机构,如图4所示。图4中,θi为各连杆之间夹角;li为各连杆长度;mi为根据机构等效的各连杆质量;O0~O8分别为仿猫机器人模型中的后肢趾关节、踝关节、膝关节、髋关节、腰部、肩关节、肘关节、腕关节和前肢趾关节;Xi和Yi分别为以Oi对应关节为圆心建立直角坐标系的X轴和Y轴。
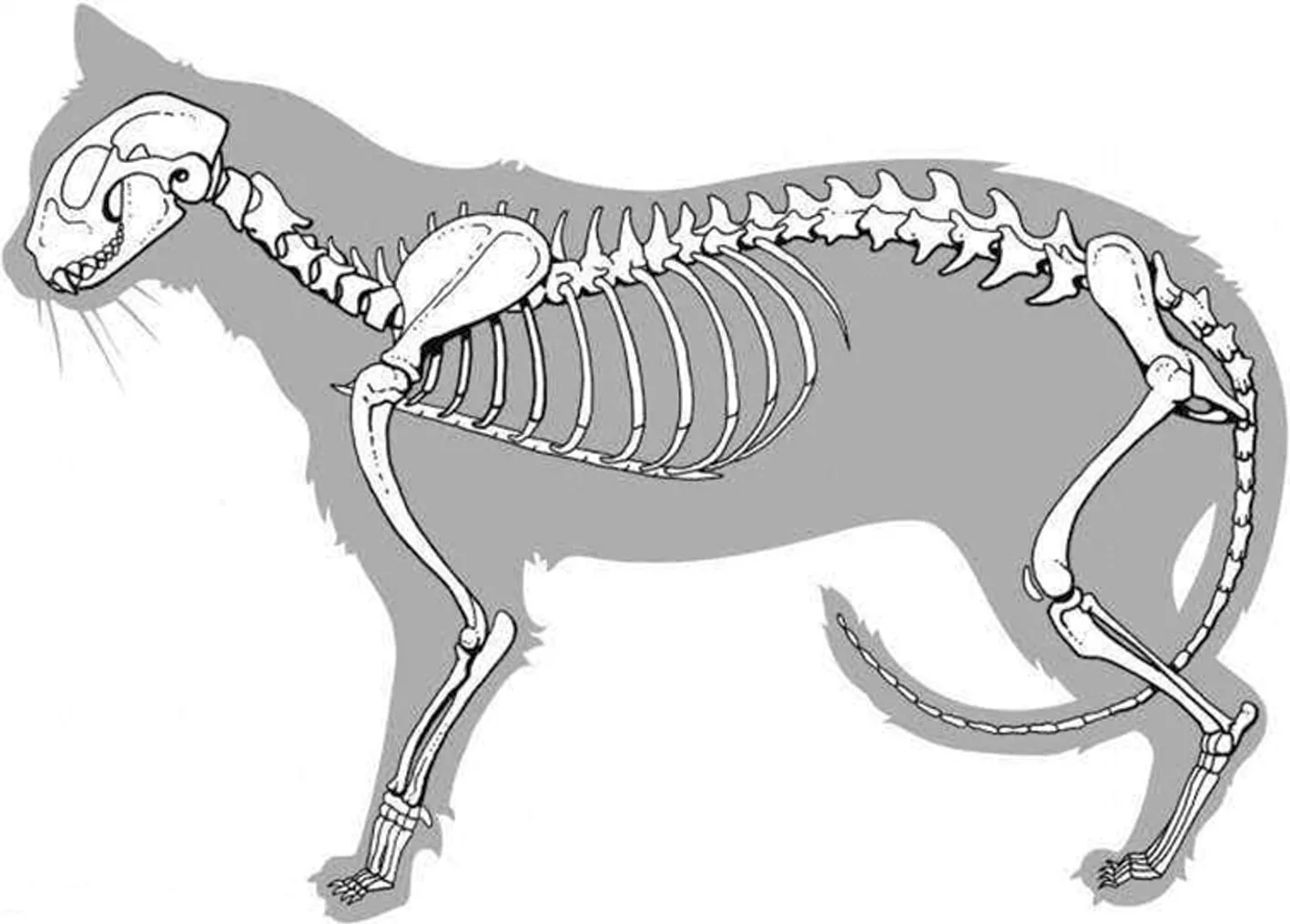
图2 家猫骨骼模型Fig.2 Cat skeleton model
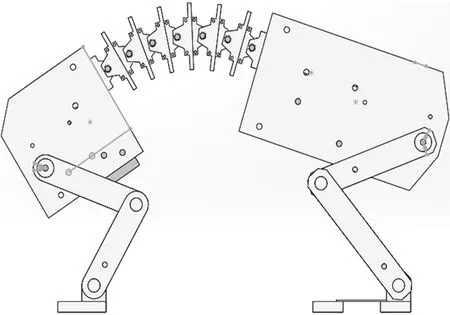
图3 仿猫跳跃机器人Fig.3 Cat-like jumping robot
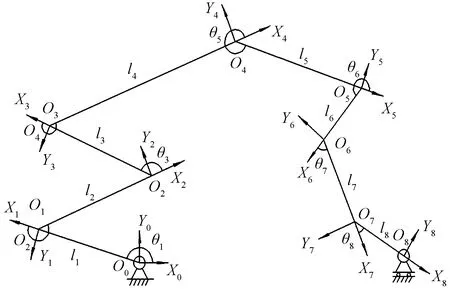
图4 仿猫跳跃机器人结构简化图Fig.4 Simplified structure of cat-like jumping robot
在Adams环境下使仿猫跳跃机器人模拟家猫跳跃,如仿真结果与家猫实际跳跃情况接近,则认为机器人机构与实验猫具有相似的运动特点,可对其进行进一步的分析。决定家猫跳跃最终结果的因素为离地瞬间的姿态及质心速度大小。根据表1,在Adams仿真中设定跳跃条件,使得仿猫跳跃机器人起跳瞬间各关节角分别为腕关节145°、肘关节70°、肩关节50°、腰部165°、髋关节135°、膝关节145°、踝关节140°、后脚趾与地面夹角80°,此姿态与家猫起跳瞬间姿态相近。Adams仿真跳跃实验结果如图5所示。仿猫跳跃机器人跳跃距离约为1.1 m,跳跃距离与家猫实际跳跃能力相符,因此认为仿猫机器人跳跃规律与家猫跳跃规律基本一致,可以用作理论分析模本。
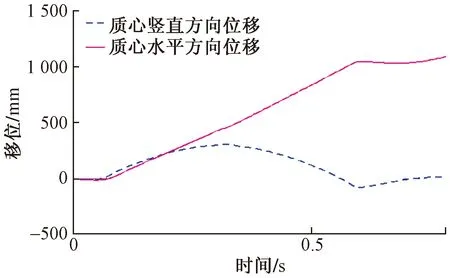
图5 Adams仿真跳跃实验结果Fig.5 Experimental results of Adams simulation jump
3 仿猫机器人起跳过程的运动学和动力学分析
3.1 仿猫机器人起跳阶段运动学分析
腰部的主要姿态变化发生在前肢开始发力到后肢发力前这一阶段,因此对这一过程进行动力学和运动学分析。利用D-H法[12]对该过程进行运动学分析,家猫在跳跃过程中左右脚同步运动,整个跳跃过程可看作在XOY平面内的运动,D-H矩阵中的α和d均为0。由于整个起跳过程中后脚趾可看作绕地面转动,因此以后脚趾为原点建立绝对坐标系,地面为零势能面,跳跃方向为X轴正方向,坐标建立如图4所示。假设仿猫机器人第i根连杆绕其质心的转动惯量为Ji。D-H参数与各连杆质量如表2所示。
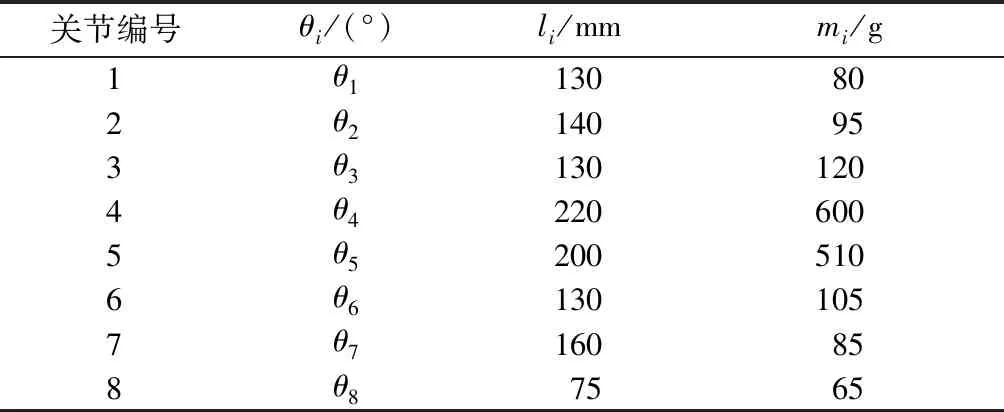
表2 D-H参数及各连杆质量Table 2 D-H parameters and connecting rod quality
在二维平面中,由D-H法可知,相邻坐标系之间变换矩阵为
式中:iTi+1为第i根杆的坐标系向第i+1根杆的坐标系变换的变换矩阵。为简化公式表达,令Si=sinθi,Ci=cosθi,Si±j=sin(θi±θj),Ci±j=cos(θi±θj)。假设每根杆质量均匀分布,每根杆的质心近似为该杆的中点。此阶段的运动学正解问题即已知各连杆夹角求解机器人各杆质心相对于后脚趾坐标系位姿的问题,各杆坐标系对后脚趾坐标系的变换矩阵为

(2)
则各连杆质心在绝对坐标系中坐标为
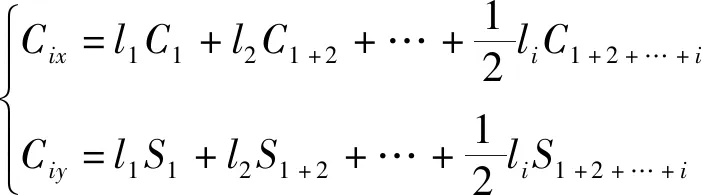
(3)
式(3)中:Cix和Ciy分别为第i根连杆质心在绝对坐标系中的横、纵坐标。
3.2 仿猫机器人起跳阶段动力学分析
以运动学分析为基础,利用拉格朗日方程推导动力学方程[13],对后腿开始发力前的跳跃过程进行动力学分析,可以得到该过程各关节力矩的变化过程。此阶段后腿还处于蓄能阶段,膝关节与踝关节基本不动,因此分析对象为前腿各关节、腰部及髋关节,此时前肢与躯干可看作绕髋关节转动。
各连杆质心方程对时间求导可得各连杆质心处水平方向和竖直方向的速度方程vix和viy:
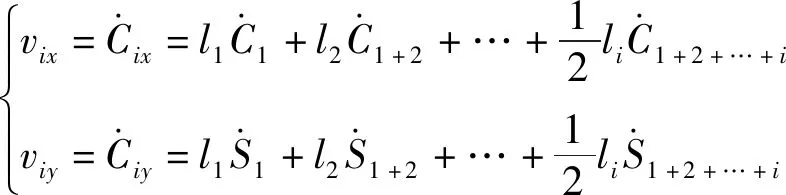
(4)
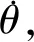
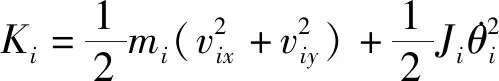
(5)
其中:
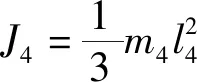
(6)
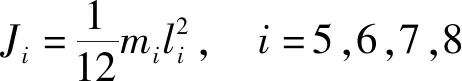
(7)
若以起跳地面为重力势能的0势能面,则各杆质心纵坐标Ciy为质心到零势能面距离,重力加速度为g=9.8 m/s2,第i根杆重力势能Pig为
Pig=migCiy
(8)
第i个关节处弹性势能Pis为
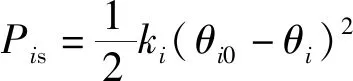
(9)
式(7)中:ki为各关节处扭簧刚度系数,θi0为各关节之间初始相对转角。
则系统总动能K为
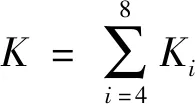
(10)
系统总势能P为
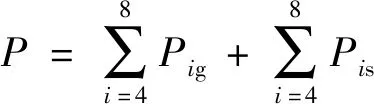
(11)
系统拉格朗日函数的表达式为
L=K-P
(12)
式(12)中:L为系统用各广义坐标和各广义速度所表示的功能。对拉格朗日函数进行求导处理,可得各关节处驱动力矩的表达式:
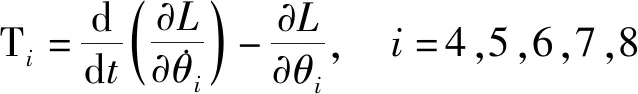
(13)
式(13)中:T4为后肢髋关节处力矩;T5为腰部驱动力矩;T6、T7、T8分别为前肢肩关节、肘关节和腕关节的力矩;t为时间。整个过程持续时间约为0.1 s,对Adams中测得的各关节角度变化进行三次拟合,各关节角度拟合为

(14)
各关节角扭簧刚度系数为k4=8 Nm/rad,k5=10 Nm/rad,k6=2.5 Nm/rad,k7=1.5 Nm/rad,k8=0.5 Nm/rad。各关节角初始相对转角为θ40=73.3°,θ50=135.2°,θ60=62.4°,θ70=-64.5°,θ80=-34.7°。再将表2中基本参数代入式(13),可得各关节力矩随时间变化规律,腰部力矩随时间变化如图6所示,其余关节力矩随时间变化如图7所示。
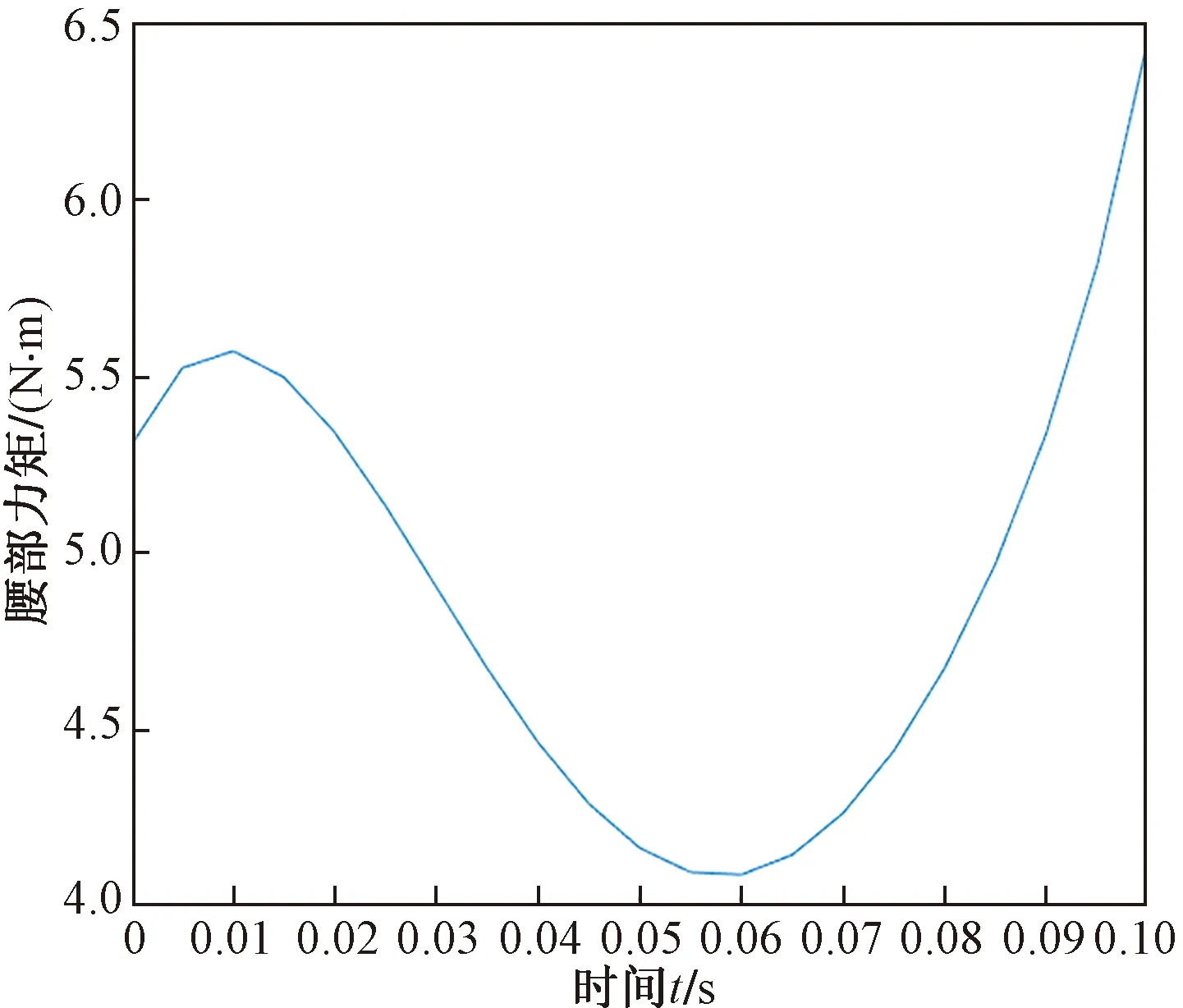
图6 腰部力矩随时间变化Fig.6 Time-varying of waist moment

T4为髋关节处力矩;T6为肩关节处力矩;T7为肘关节处力矩;T8为腕关节处力矩图7 各关节力矩随时间变化Fig.7 Time-varying of joint moments
由图6、图7可知,起跳瞬间腰部与前肢同时发力,随着前肢持续做功,腰部力矩逐渐减小。时间t约为0.06 s时前腿完全离开地面,此时前腿不再对外做功,为克服前肢与躯干重力髋关节处力矩逐渐增加。此时腰部力矩逐渐增大,带动前肢继续运动,使前肢与前部躯干继续绕质心旋转,增大了前肢与前部躯干绕质心的角动量。根据 Zajac[14]对猫的极大跳跃的研究,家猫在起跳前腰部运动会给质心提供很大一部分跳跃所需角动量,这与分析得到结论相符。
4 仿猫机器人腰部初始夹角与机构起跳阶段所需做功关系
在Adams中测得起跳瞬间质心速度为v=[vx,vy]=[2.1 m/s,2.4 m/s],起跳瞬间各关节角为θ1=80°、θ2=140°、θ3=-145°、θ4=145°、θ5=165°、θ6=50°、θ7=-75°、θ8=135°。则由式(5)、式(10)得到起跳时动能E和起跳时势能Pll。给定准备状态各关节夹角θ10=150°、θ20=55°、θ30=-90°、θ70=-65°、θ80=-35°,前脚趾与地面夹角为10°,根据此时姿态可得机构前后肢重力势能为常数,θ40、θ60随着θ50变化而变化。准备状态重力势能为
PI=0.63+m4gC4y+m5gC5y
(15)
初始状态的腰部夹角θ满足:
θ=θ50
(16)
若要满足相同的起跳条件,机构需要做的功为
W=Pll+E-Pl
(17)
当起跳过程没有腰部辅助跳跃时,整个起跳过程躯干可看作一个整体,θ5始终为180°,腰部在起跳过程中始终没有力矩。当前肢与后肢起跳的准备姿态与有腰部辅助跳跃准备姿态一致时,由式(15)可得到机构此时的重力势能。根据式(17)可得到初始位置腰部夹角与机构满足相同起跳条件所需做功关系。
机构做功来自于各关节处扭簧释放的弹性势能,扭簧储存的弹性势能来自于起跳前对各关节的压缩。由图8可知,有腰部辅助跳跃时,起跳瞬间腰部夹角越小机构所需做功越少,没有腰部辅助跳跃时机构所需做功最多。家猫在开始跳跃前都会尽可能拱起脊柱,减小腰部夹角,这与分析验证所得结果一致。在起跳前,机构通过姿态调整储存能量为跳跃做准备。在前后肢各关节压缩角度相同的情况下,腰部的姿态调整可以在增加腰部弹性势能的同时减小机构到起跳姿态所需增加的重力势能。腰部的姿态调整把一部分起跳阶段需要做的功在起跳的准备阶段提前完成,减小起跳阶段所需做功,使整个跳跃过程能量分配更平滑。若没有腰部辅助跳跃,在前后肢开始起跳瞬间姿态一定时,机构不能在起跳的准备阶段进行姿态调整,且没有腰部辅助跳跃时比有腰部辅助跳跃时少一个驱动关节,除机构所需做的总功更多外,前后肢各关节所需做功也将变多,使得运动效率降低。
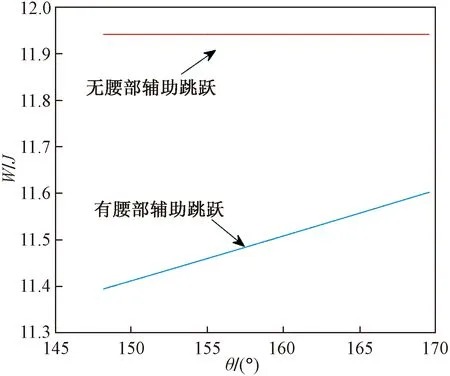
图8 初始位置腰部夹角与机构所需做功关系Fig.8 The relationship between the waist angle at the initial position and the work required by the mechanism
5 结论
在家猫生物原型的基础上建立仿猫机器人的机构模型,并对其进行仿真实验及动力学运动学分析。得出以下结论。
(1)根据仿生学研究的基本方法,依照家猫跳跃规律对仿猫跳跃机器人进行仿真。对仿猫跳跃机器人进行了结构简化并进行了动力学和运动学分析。通过腰部力矩变化说明了腰部可为起跳时质心提供所需的角动量。
(2)通过能量的角度分析了起跳过程初始阶段腰部夹角和达到相同起跳状态机构所需做功的关系,在起跳的准备阶段,腰部初始夹角越小,机构所需做功越少。这与自然界家猫的运动规律相符合。
(3)对比了有腰部辅助跳跃时和无腰部辅助跳跃时的区别。对仿猫跳跃机器人而言,当有腰部辅助跳跃时,可以在起跳的准备阶段更好地进行姿态调整,跳高跳跃效率。
算例中家猫各肢体位姿数据根据Adams仿真得到,与实际姿态存在误差,且生物学基本参数与实际家猫的生物学参数也有出入,但结论趋势反映了家猫起跳阶段的一般规律,为仿猫机器人的改进和跳跃运动的控制提供了理论基础。

