LAMBDA 算法在GPS 载体姿态测量中的应用
牛慧军,杨开伟
(1.解放军92941 部队,葫芦岛 125000;2.中国电子科技集团公司第54 研究所,石家庄 050081;3.卫星导航系统与装备技术国家重点实验室,石家庄 050081)
1 GPS 姿态测量
GPS 姿态测量在GPS 应用中得到了快速的发展,在国民经济各个领域得到广泛的应用,同时也是航海、航天及陆基导航系统中的关键技术之一。GPS 载波相位动态差分定位技术的发展,尤其在工程测量中更是显示出其优越性。载波相位差分定位是目前精度最高的卫星导航定位方式,在几米长的基线内可获得毫米级精度,载波相位差分定位技术的突出特点为船舶姿态角的测量开辟了新的途径,并提供了有力的技术支持。获得高精度的姿态角关键是要得到高精度的相对位置,GPS 测姿的核心技术是载波相位的高精度测量和整周模糊度的快速正确解算。整周模糊度的求解方法有多种,其中优缺点各不相同,利用LAMBDA 算法来求解整周模糊度将有效提高正确性和可靠性。
2 GPS 姿态测量的方法与实验
2.1 GPS 测姿原理
GPS 载体测量测量主要是通过各个GPS 天线和接收机进行信号接收观测,利用各接收机生成的GPS 伪距和载波相位观测数据来确定载波相位模糊度,进而通过相对差分定位来得到各个天线之间的相对位置。在相对位置的基础上,通过矩阵旋转和坐标转换关系计算出载体的姿态角。

图1 船舶姿态角定义
载体姿态角由航向角k、横摇角θ、纵摇角ψ 来定义,如图1所示。姿态角(k,θ,ψ)的测量采用载体坐标系,其中,Y 轴与首尾线一致,指向航行方向,载体坐标系为相对于当地水平面的地平坐标,即YX 平面位于载体所在点的水平面。



载体航向角k 是地理北顺时针旋转至Y 轴的夹角,若已知Y轴上任意两点的大地坐标则可算出k 角。
四元素又称欧拉对称参数,是载体姿态表示的另一种方法。如果空间中存在两个原点重合的直角坐标系,那么总存在一条不变轴和一个α 角度,其中一个直角坐标系绕不变轴旋转α 度后,能与另一个直角坐标系完全重合。这种姿态表示法可用四个参数来定义:
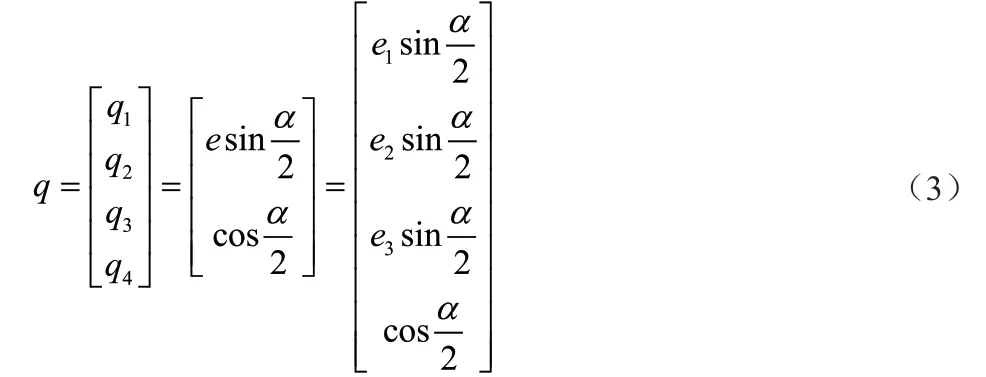
式中,e1,e2,e3是旋转轴的方向矢量。

同时改变四个参数的符号,不影响载体姿态的计算结果。由于四元素法不能很好的反应载体姿态的物理特性,没能得到广泛的应用,而欧拉角法可以清楚的表达载体姿态的物理特性,所以在GPS 姿态测量中得到普遍应用。
2.2 测姿方案
为了得到计算载体姿态角所需的坐标分量,在载体上沿首尾线纵轴和垂直于纵轴的一侧或双侧安装接收天线,形成3天线或4天线姿态测量系统。多天线共用一个接收机,由于所有卫星信号的瞬时相位与同一本机参考信号的相位比较,所得到的观测量已不存在接收机钟差。天线间的距离事先精确测定,作为快速求解载波相位模糊度的约束条件,可加速模糊度求解过程。如果条件所限,天线的位置不必纵向横向正交安置,各天线也不必共用一接收机。经载波相位差分定位可得到各天线间的相对位置,在差分定位中以任一天线的当前位置作为已知点。GPS 定位结果采用WGS-84坐标系,为了得到载体坐标系下的相对位置需进行坐标变换。进行坐标变换时,通常选取首尾线船尾一侧的天线位置为坐标原点,其纬度为φ0,经度为λ0,高程为h0。由首尾线上两天线的大地坐标求得航向为k,设舰船上其他任一天线在WGS-84直角坐标系下的坐标为(xG,xG,zG),在载体坐标系下的坐标为(x,x,z),坐标转换关系为:
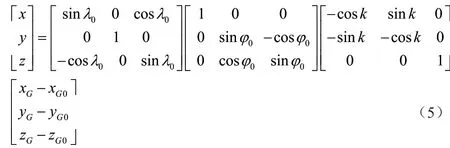
yG0=(n0+h0)cosφ0sinλ0;zG0=[n0(1-e2)+h0]|sinφ0;n0=a(1-e2sin2φ0)1/2;
由各天线在载体坐标系下的坐标分量可求得两天线间的相对位置,进而求得姿态角。
用载波相位差分法求解姿态时,一个重要的问题是解算整周模糊度,准确获得载波相位的整周模糊度是GPS 姿态测量的关键,目前常用的整周模糊度解算方法是LAMBDA 算法。
3 LAMBDA 算法求解整周模糊度
采用最小二乘模糊度去相关调整算法(简称LAMBDA)具有完善的理论体系和较好的性能,在模糊度解算中是一种较为理想的方法。其载波相位观测方程的数学模型为:
y=Aa+Bb+e
式中,y 为双差载波相位观测量;a 为未知整周模糊度向量;b 为未知位置参数向量;A 为模糊度系数矩阵;B 为方向矩阵;e为双差模式下的观测误差向量。求解过程包括模糊度去相关处理和模糊度整数搜索。
3.1 模糊度去相关处理
整数高斯去相关法可以显著减小模糊度间的相关性,该方法要求变换过程中元素保持整数特性。首先进行高斯变换:

变换后得到:

要使变换后的模糊度不相关,应该满足:

即

模糊度变换矩阵Z 具体构造方法如下:
(1)通过进行二维模糊度变换,得到变换矩阵。
(2)进行变换后的方差-协方差阵计算:

(3)根据门限判断是否结束变换,若不满足门限,则重复步骤(1)、(2);若满足门限,得到Z2,…,ZK。
(4)确定变换矩阵:Z=ZK…Z2Z1。
3.2 模糊度整数搜索
得到模糊度去相关变换矩阵后,用该矩阵构造新的相关程度较低的模糊度集合。新的模糊度向量用Z 表示,其最小二乘估计和方差-协方差矩阵通过下式来得到:

双差模糊度搜索空间可变为:

转化后的模糊度搜索空间的展开形式为:

从最后一个模糊度开始搜索计算,有初始关系式:

利用计算得到的αn整数值来计算αn-1,依此类推,直到α1。
4 仿真
仿真测试实验分为3米基线和1米基线两组,对本文测姿方法进行测试分析。设定基线为3米,仿真次数为400次时,得到姿态误差曲线如图2所示:

图2 基线3米姿态角误差曲线图
设定基线为1米,仿真次数为400次时,得到姿态误差曲线如图3所示:
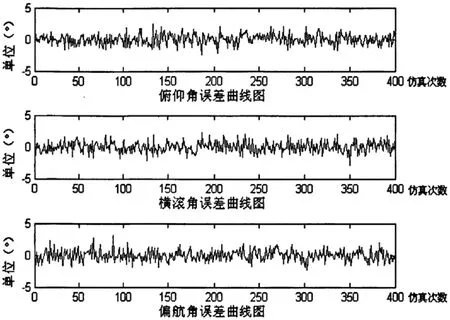
图3 基线1米姿态角误差曲线图
姿态角误差统计如表1所示:

表1 姿态角误差统计表
通过仿真实验及结果分析可知,LAMBDA 算法在GPS 载体姿态测量中应用是可行的,3米基线长度各姿态角测量精度均优于0.085°;1米基线长度各姿态角测量精度均优于0.85°。
5 结束语
采用载波相位测量与差分技术进行GPS 测姿已是当前应用的主要方法,本文利用载波相位差分定位方法,并通过LAMBDA算法求解载波相位整周模糊度来实现高精度姿态测量。通过仿真实验和数据分析证明,该方法可行,并且测姿精度能够满足使用需求,具有实际工程意义。

