非定常对流占优扩散方程的龙格库塔伽辽金有限元方法

冯立伟, 席 伟

(1.沈阳化工大学 数理系，辽宁 沈阳 110142； 2.沈阳化工大学 计算机科学与技术学院，辽宁 沈阳 110142)

大量的自然现象的理论模型是对流扩散方程，如海水中热量和盐分的变化、大气和水体中污染物的流动分布、药物在人体中的流动和稀释代谢等[1-3].所以，对流扩散方程的求解方法研究早已成为重要的研究领域.有限差分法、谱元法、有限元法是求解对流扩散方程的典型方法[4-7].但是，在对流占优扩散方程中，由于对流现象起主要作用，扩散现象比较微弱，导致传统有限元方法产生伪数值振荡[8-10]，使得求解失败.流线扩散有限元(streamline diffusion,SD)[8,10]通过在检验函数上沿流场方向添加人工黏性项，提高其解的稳定性，但其未考虑时间效应，只能求解稳态对流扩散问题.对于发展型对流扩散问题，由于物质在空间的分布随时间发生变化，经典求解方法为时空有限元，但其将时间项与空间项同等对待，导致求解维数较高，显著增加了算法的计算复杂度.另一求解方法为差分流线扩散有限元[11-13](finite difference streamline diffusion,FDSD)，其在时间方向上采用差分离散，空间上使用流线扩散有限元，成功抑制了数值振荡的产生.但是，由于其在检验函数上添加流线项，导致变分方程的每一项都对应添加了流线项，使得求解格式复杂，计算量显著增大.本文对非定常对流占优扩散方程给出一种新的求解方法：首先，在扩散项上引入拟合因子来抑制伪数值振荡；其次，使用伽辽金有限元方法将方程转化为半离散化常微分方程；最后，使用四阶四级龙格库塔方法将常微分方程转变为线性方程组，从而获得其数值解.对求解方法进行了理论分析，并给出了详细的计算过程.使用一个数值例子和天然气管道泄漏实例进行了实验，实验结果验证了方法的有效性.

1 计算格式描述

非定常对流占优扩散方程的初边值问题:

(1)

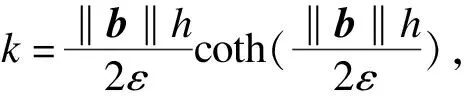
(f,v)，∀v∈V.

定义两个泛函：

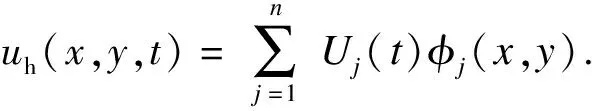
此变分问题的Galerkin有限元离散为求uh(·;t)∈Uh，使得

(2)

成立.将式(2)改写为半离散化常微分方程组

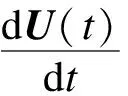
(3)

对此方程组再采用四阶四级龙格库塔法离散时间导数项，得到全离散化线性方程组

按时间层，逐层推进可求得各时间层上每个网格节点上数值解.

2 详细计算过程

2.1 空间Galerkin有限元半离散格式

对空间区域进行三角形网格剖分，获得网格节点坐标、单元信息以及边界节点和边界单元信息，并对各单元和节点分别进行编号.在第k个剖分单元ek上使用一次线性形状函数Ni、Nj、Nm，则

uh(x,y,t)=Ni(x,y)Ui(t)+Nj(x,y)Uj(t)+

Nm(x,y)Um(t),(x,y)∈e.

上式简记为uh=NUe(t),同理vh=NVe，记uh=BUe,vh=BVe，代入近似变分方程(2)，方程(2)中的各项计算如下：

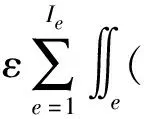
cNTN+εBTB)dxdy

)Ue+

其中：Ue=CU,Ve=CV，Me、Ke、Fe分别为单元e质量矩阵、单元刚度矩阵和单元荷载向量，M、K、F分别为总质量矩阵、总刚度矩阵和总荷载向量.此时，变分方程(2)变为

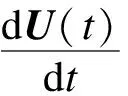
因为V是任意的，所以上式变为

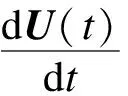
2.2 单元计算及总体合成

Ke=∬e(NTb·B+cNTN+εBTB)dxdy+

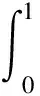
由于单元质量矩阵中被积函数为多项式函数，可采用欧拉积分计算.由于源项形式不唯一，依赖于具体求解问题，在单元刚度矩阵和单元荷载向量中与其有关的积分，可以采用高斯型积分公式

在求得单元质量矩阵、单元刚度矩阵和单元荷载向量后，并按本单元所包含的节点的编号将其叠加获得总质量矩阵M、总刚度矩阵K和总荷载向量F，从而得到常微分方程组式(3).

2.3 常微分方程组离散求解

将常微分方程组(3)改写为

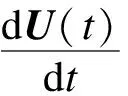
为了获得高精度解，对此常微分方程采用四阶四级龙格库塔有限差分法离散为

(4)

其中：k1=(Fn-1-KUn-1)，

全离散化线性方程组(4)可简记为

AUn=bn-1.

(5)

2.4 方程初边界条件的加载

2.5 计算程序的编写

根据上面的详细计算过程描述，给出了求解方法的算法流程(图1)，通过使用MATLAB编程实现.根据具体问题，编写求解区域的几何描述矩阵g，将求解区域进行三角形剖分，获得三角形单元矩阵t、节点坐标矩阵p和边界单元矩阵e，可使用MATLAB函数initmesh(g,h)实现.编写主函数MassStiffnessLoadCalculate计算各个时刻的总质量矩阵、总刚度矩阵和总荷载向量，并对它们进行总体组装，获得求解常微分方程的龙格库塔法中系数及右端，再按照式(4)获得线性方程组式(5)，最后线性方程组采用双共轭梯度法进行求解.其中主函数通过调用子函数ElementMassStiffnessLoadCalculate实现单元上的质量矩阵、刚度矩阵和荷载向量的计算.另外，单元计算上述两类积分，分别编写函数EulerIntegral、GaussIntegral2D和GaussIntegral1D实现标准三角形单元上的高斯重积分和标准边界单元上的高斯线积分.编写函数DealFirstBounCond采用置1法实现第一类边界条件的加载.先划掉系数矩阵A的该节点对应行和列中的元素，并按上述修正右端列向量b的其余行，得到最终的线性方程组.使用pdemesh和pdecont函数分别绘制最终时刻的解及解的等值线图像.

图1 算法流程

3 数值实验

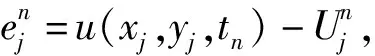
3.1 数值算例

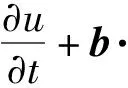
Ω=[0,1]×[0,1].

其中：b=(1 1),c=1,f=e-ty(1-y)(1-2x+2ε)+e-tx(1-x)(1-2y+2ε)，ε=0.001.其解析解为u=e-txy(1-x)(1-y).采用三角形网格，空间网格最大尺寸为0.05，时间步长为0.01，计算到最终时刻的结果见图2，误差见图3.在不同空间和时间剖分尺寸下，最终时刻的总体相对误差见表1.

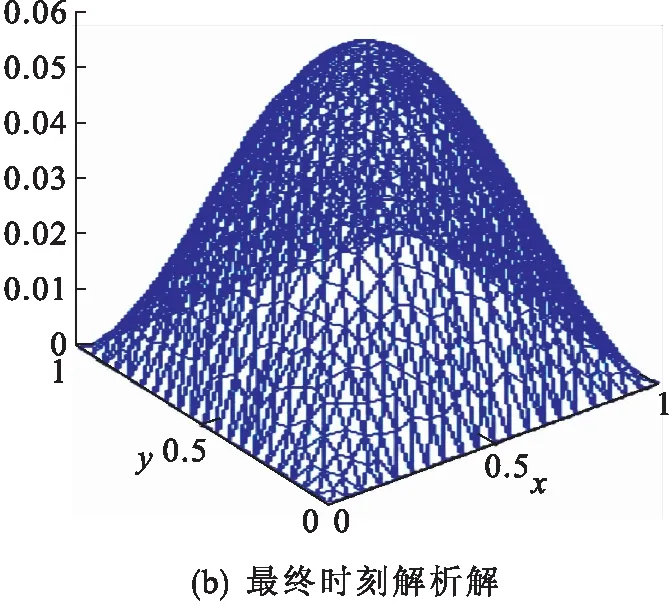
图2 数值解与解析解

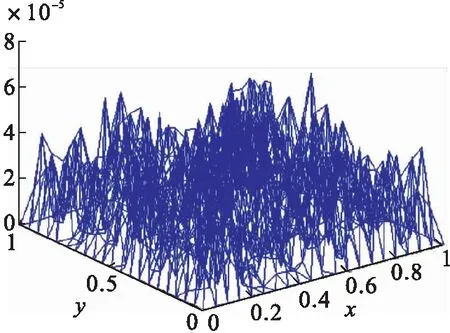
图3 最终时刻的误差

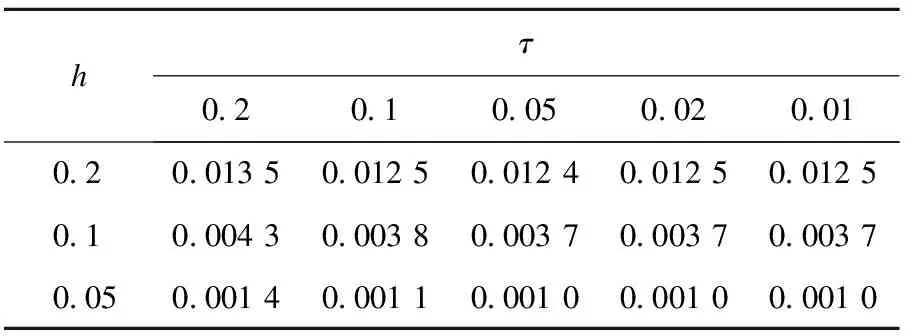
表1 相对误差

3.2 管道泄漏模拟

对半径为1 m的天然气管道的泄漏进行数值模拟，天然气泄漏的水平速度和竖直速度b=[1,0.7]m/s，扩散系数ε=0.5，在管道45°角处有一半径为0.1 m的缺口，以f=300 m/s的速度向外泄漏天然气，使用时间步长τ=0.001 s，空间最大网格尺寸h=0.1 m，图4为四分之一管道周围空间的网格剖分结果，求得的各个时刻的天然气浓度等值线如图5所示.从图5可看出：计算方法能够较好地模拟天然气的泄漏.

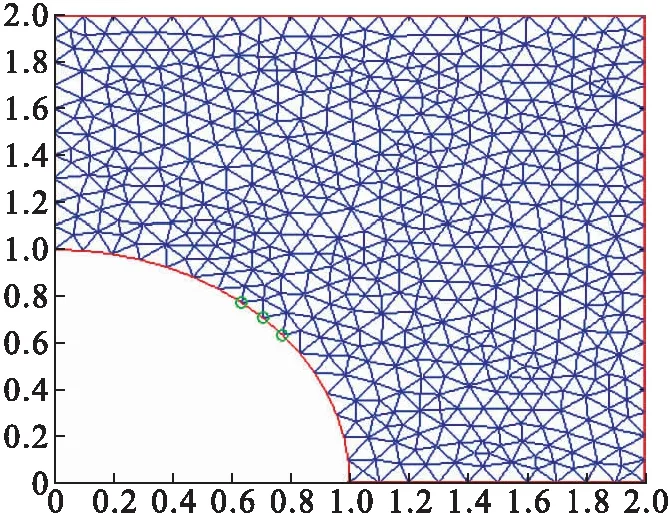
图4 天然气泄漏模型网格剖分

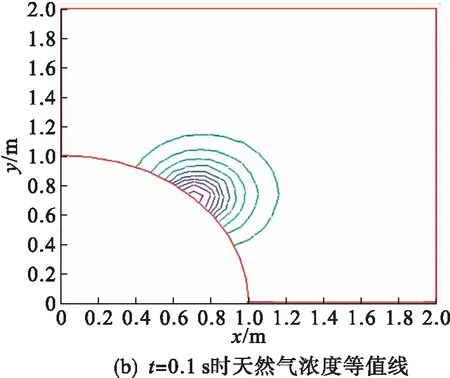
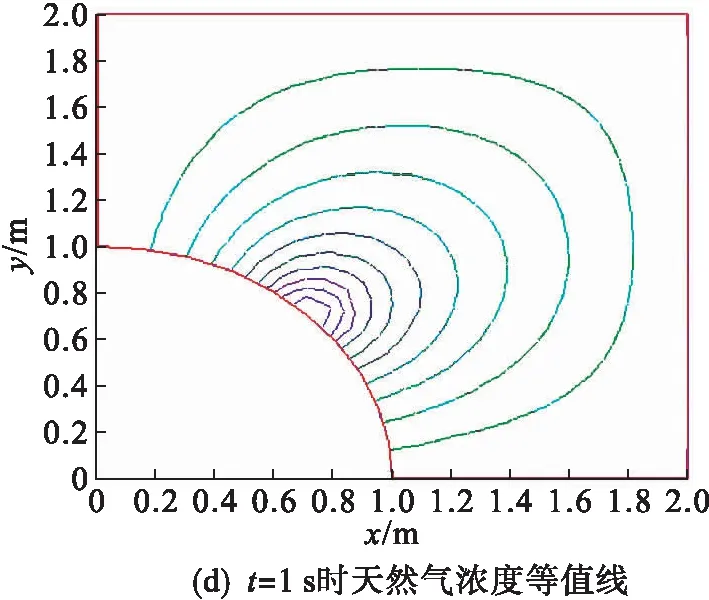
图5 各个时刻的天然气浓度等值线

4 结 论

通过在对流项上添加拟合因子消除对流占优的不利影响，并联合使用四阶四级龙格库塔方法和伽辽金有限元方法，得到了对流占优扩散方程的一种求解方法.对方法进行了详细阐述，并进行了数值实验和天然气泄漏实验.拟合因子抑制了伪数值振荡，成功实现了对流占优扩散方程的求解.