非同量分数阶永磁电机的混沌运动仿真
韩建群

摘 要:永磁電机工作在分数阶状态是一种更加普遍的电机工作情况,分数阶永磁电机在特定环境下会出现混沌运行状态,其混沌运行时存在运用整数阶微分模块进行分数阶仿真困难的问题。本文针对非同量分数阶永磁电机的混沌仿真问题,通过滤波器方法搭建了分数阶永磁电机的仿真模型,并给出了分数阶永磁电机混沌状态运行相图。仿真计算结果表明,该方法是有效的。
关键词:非同量;分数阶;永磁电机;混沌;仿真
中图分类号:TM622文献标识码:A文章编号:1003-5168(2020)07-0037-04
Abstract: It is a more common case that the permanent magnet synchronous motor works in fractional order state. The fractional order permanent magnet synchronous motor can be chaotic in a specific environment. It is difficult to use integral order differential module for fractional order simulation in chaotic operation. In this paper, the simulation model of fractional permanent magnet synchronous motor was built by the filter method, and the phase diagram of fractional permanent magnet synchronous motor in chaotic state was given. The simulation results show that the method is effective.
Keywords: non-homogeneous;fractional order;permanent magnet synchronous motor;chaos;simulation
1 研究背景
永磁同步电机(Permanent-magnet Synchronous Motor,PMSM)是一种具有高可靠性、高效率和快速动态响应等优点的驱动设备,被广泛应用于机器人、医疗设备、汽车电子等多种工程领域[1-3]。目前,关于分数阶PMSM的研究渐成热点。因为PMSM中广泛存在的机械摩擦与冲击、阻尼、齿隙动态等物理对象具有分数阶特性[4-5],实际电容和电感也具有分数阶特性[4],具有机械摩擦与冲击、阻尼、齿隙动态以及电容、电感等储能元件特性的电机也应该是具有分数阶的,因此采用分数阶微积分建立电机的数学模型能更加细腻地刻画其动态行为,更为准确地描述其属性特征[6]。
PMSM在工程中常常工作在额定转速和转矩状态,从而保证电机的高效率。但是,在实际应用中,由于机械工作环境的变化,在特殊条件下,PMSM也呈现出混沌状态,即电机的转速和转矩是间歇振荡的,从而导致电机的控制性能不稳定,并且产生不规则的电磁噪声[7]。从当前的研究结果可知,分数阶PMSM系统会表现出混沌状态。这促使人们利用分数阶微积分理论更深入地研究混沌这一自然界普遍存在的物理现象,并探索分数阶系统中的混沌控制与同步方法[8-9]。近年来,有学者利用分数阶微积分建立了分数阶PMSM系统模型,并通过稳定性理论分析、分数阶系统的时域数值求解以及Lyapunov指数计算对系统混沌动力学特性进行研究,并给出了同量分数阶PMSM系统出现混沌运动现象的最低阶次及控制方法的有效性。
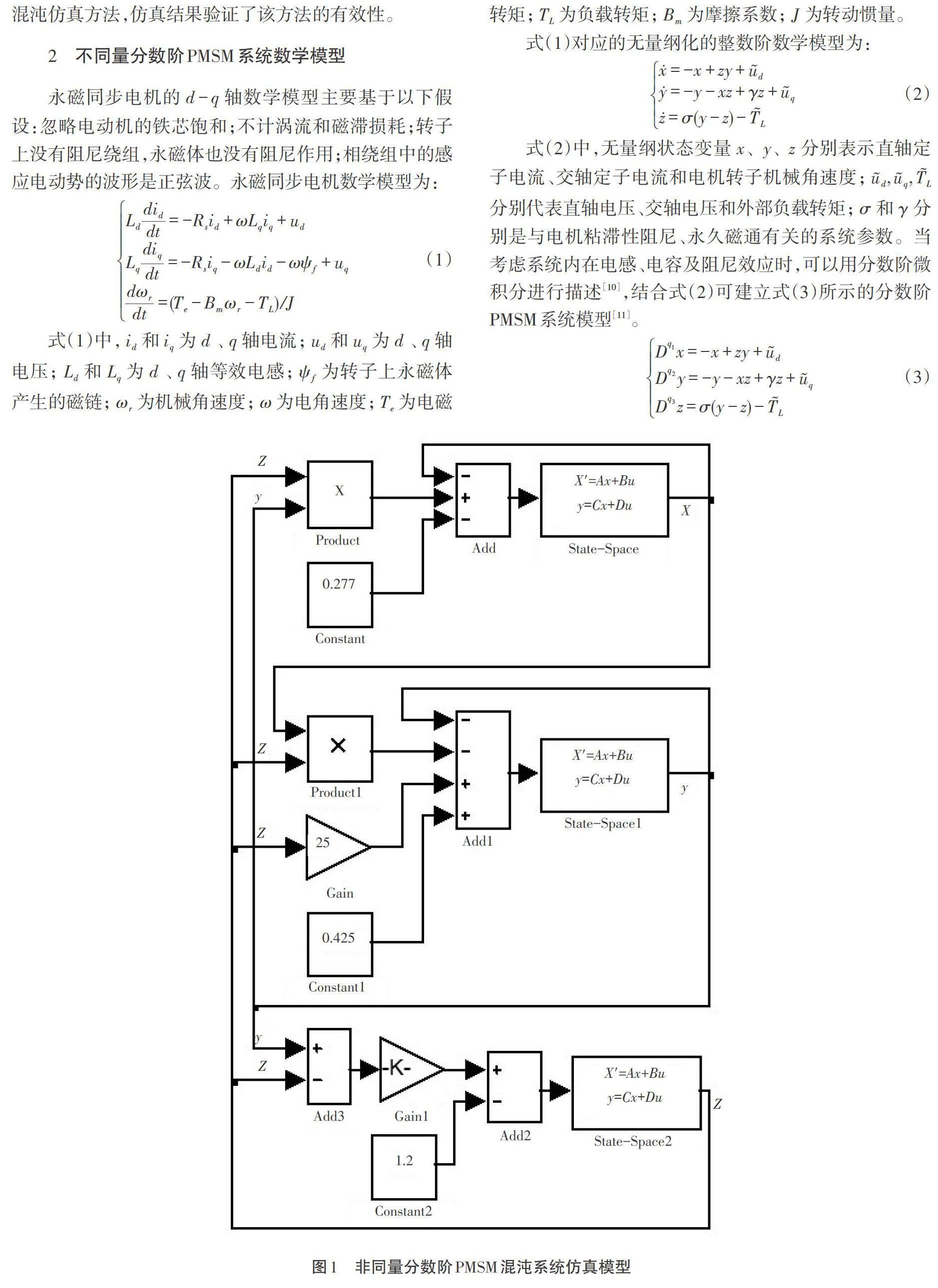
当采用MATLAB软件对PMSM运行状态进行仿真时,需要对整数阶仿真模块进行改进才能完成分数阶PMSM系统状态仿真。本文研究了不同量分数阶PMSM混沌仿真方法,仿真结果验证了该方法的有效性。
2 不同量分数阶PMSM系统数学模型
4 结论
分数阶PMSM是电机研究领域热点之一。本文对非同量分数阶PMSM系统进行介绍,研究了运用滤波器进行分数阶仿真的方法,并运用分数阶算子的State-space模块建立了分数阶PMSM仿真系统,并给出了分数阶PMSM系统混沌运行的仿真结果。
参考文献:
[1]Zheng P, Bai J , Song Z, et al. Development of the compound-structure electrical machine and its key technologies for hybrid electric vehicles[J]. Journal of Harbin Institute of Technology,2016(3):1-10.
[2]赵佳奇.永磁同步发电机无速度传感器控制[J].控制工程,2016(11):52-56.
[3] Miao L , Zhang Y , Tong C , et al. Efficiency Optimization of Permanent Magnet Synchronous Generators Based on Model Predictive Direct Torque Control[J]. Diangong Jishu Xuebao/Transactions of China Electrotechnical Society,2018(15):3535-3546.
[4]Faqiang W,Xikui M. Fractional order modeling and simulation analysis of Boost converter in continuous conduction mode operation[J]. Acta Physica Sinica,2011(7):89-96.
[5] Barbosa R S , Machado J A T . Describing Function Analysis of Systems with Impacts and Backlash[J]. Nonlinear Dynamics,2002(1-4):235-250.
[6]赵远征.分数阶控制算法在永磁交流伺服系统中的研究与应用[D].南京:南京理工大学,2014.
[7] Chen J H , Chau K T , Chan C C . Chaos in voltage-mode controlled DC drive systems[J]. International Journal of Electronics,1999(7):857-874.
[8] Matouk A E . Chaos, feedback control and synchronization of a fractional-order modified Autonomous Van der Pol-Duffing circuit[J]. Communications in Nonlinear Science and Numerical Simulation,2011(2):975-986.
[9] Tavazoei M S , Haeri M . Synchronization of chaotic fractional-order systems via active sliding mode controller[J]. Physica A: Statistical Mechanics and its Applications,2008(1):57-70.
[10]陈文,孙洪广,李希成,等.力学与工程问题分数阶导数建模[M].北京:科学出版社,2010.
[11]Huang G Q , Wu X .Analysis of Permanent-magnet Synchronous Motor Chaos System[C]//Lecture Notes in Computer Science, Artificial Intelligence and Computational Intelligence. Berilin:Springer.
[12]高遠,范健文,罗文广,等.分数阶永磁同步电机的混沌运动及其控制研究[J].武汉理工大学学报,2012(7):134-140.

