某埋入式进气道气动优化设计及试验研究

徐志超?赵振山?冯剑

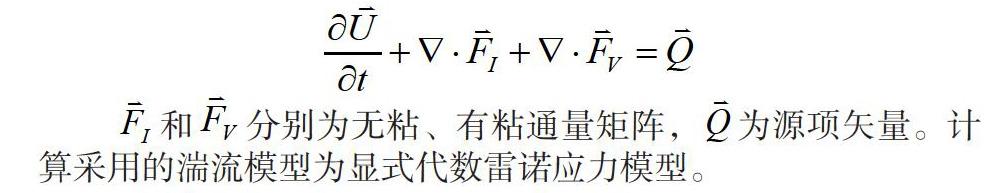
摘 要 针对某埋入式进气道基础构型，开展特定来流条件下的数值模拟，针对进气道内、外流场特性进行分析;在对进气道基础构型气动、流场特性分析的基础上，设计进气道几何构型的若干优化方案;针对多组优化构型进行数值模拟，并与基础构型对比，获得更高性能的进气道优化构型;采用风洞试验对基础构型、优化构型进行研究验证，确认进气道优化方案气动特性显著优于基础方案。

关键词 埋入式进气道;气动特性;优化设计;数值模拟;风洞试验

引言

埋入式进气道由于其与飞行器机身融于一体的设计特点，除了能有效地减少雷达散射截面积，提高飞行器的生存能力外，还能大幅度地减小飞行器的迎风面积，降低迎风阻力。埋入式进气道的设计及其性能的研究已引起了国内外的广泛注意[1-4]。

埋入式进气道的特点是：①进口埋入机身或机翼的常规外形之中，气流经过一个缓慢倾斜的长斜板通道引人进口。②该斜板初始端狭窄，其扩散的尖缘侧壁一直连到进口展向的末端。这种精巧设计的作用在于扩散侧壁切断流线，产生一个涡的运动，把斜板附面层扫向旁边，并使一部分附面层通过进口的两端流向外流区。

在国外，美国的ACM和ACM-129巡航弹采用了埋入式进气道，确认其高亚速性能已达到了实用程度。在国内，研究人员亦对埋入式进气道进行了系列研究，郭荣伟等提出了气动S弯概念，即进气道的内、外流管呈S弯形状;夏阳运用这一方法成功地设计出一个三维埋入式进气道;杨爱玲对该种埋入式进气道进行了二维数值分析和流场的雷诺应力测量及频谱分析[5-6]。

近年的研究表明，尽管埋入式进气道一般情况下不能直接利用来流冲压，容易导致总压恢复降低，甚至导致摄入空气流量不足，但是通过精细化设计内管道和唇口的气动型面，还是可以在一定程度上实现增大气流摄入，提高性能、降低畸变效果。当前，通过对埋入式进气道设计优化以提升其性能，是该类型进气道研究的一个重点。

1基础构型流场特性

1.1 控制方程及湍流模型

全机流场计算基于求解N-S方程。笛卡儿坐标系下雷诺平均N-S方程（RANS）方程为[7-8]：

和分别为无粘、有粘通量矩阵，为源项矢量。计算采用的湍流模型为显式代数雷诺应力模型。

1.2 计算数模提取

基于CFD数值模拟技术对进气道性能进行评估时，数模提取时可以忽略尾部舵面，同时需要对进气道出口，也就是进气道、发动机气动交接面增加延长段以使该处流动自由发展，便于边界条件的设定和测量，后延长段长度为2.0D（D为AIP截面圆环外径）。

1.3 基础构型结果分析

通过对数值模拟得到的流场特性分析可得以下结论：该状态下进气道部分区域存在流场分离，其流动分离受进气道型面、进气道/弹体衔接位置以及入口形状的影响，导致进入进气道的气流在逆压梯度作用下产生局部流动分离。进气道流动分离最终导致进气道AIP上部存在明显的低总压区，造成进气道整体气动性能较差。

2进气道优化设计方法[9-11]

2.1 优化设计参数选择

埋入式进气道优化设计主要考虑以下参数：

（1）进气道的中心线形状的设计。

（2）截面积沿程分布规律的设计。

（3）降低流场畸变、增加总压恢复的喉道参数设计。

（4）进气道唇口修型。

2.2 气动S弯设计优化

气流经过埋入式进气道进气口时会形成一种类似S弯进气道第一弯段的扁流管，与内流管一起形成一个气动S弯管。根据这一气动S弯概念可知，如果设计出合适的管道型面和唇口，就可充分提高该气动S弯管的冲压效率，使进气道的总压恢复提高，畸变减小，因此，埋入式进气道内管道设计可以借鉴S形进气道的设计方法。即先根据几何参数和流量要求设计出S形进气道，然后该S形进气道和机身在指定位置按指定方式相贯形成埋入式进气道。

2.3 中心线设计

中心线形状的设计是埋入式进气道设计的关键技术之一，因为中心线的形状决定了气流在进气道的偏转情况，弯曲通道内，气流由于受离心力的作用，流场分布不均匀，畸变较大。中心线形状的设计直接影响到进气道的气动性能。中线线坐标主要参考以下变化函数：

（1）均匀变化：

（2）前缓后急：

（3）前急后缓：

2.4 面积律设计

扩压管截面形状对它的性能有影响，同样面积率对进气道性能的影响显著。埋入式进气道的面积分布规律决定了管内流向扩压比的变化，不合适的面积分布加上弯曲通道内气流受离心力的作用，埋入式进气道内的流动很容易出现分离。

埋入式进气道通道面积适合先略微缩小，后扩大，再变平缓，在一定程度上对气流起了一个缓冲作用，改善了进气道出口的流场分布，从而大幅度地降低了进气道出口的流场畸变值。

2.5 喉道及唇口设计

進气道喉道设计面积是超音速进气道主要的控制参数之一。喉道马赫数既反映进气道空气流量的大小，也反映进气道的流动状态，对进气道性能有直接影响。对亚音速进气道，可以不设置喉道，从进气道进口到出口全部为扩散段，但是，一般亚音速进气道还是需要喉道设计，其主要的作用是对进气流动进行整流，可以降低出口流场畸变。

对于唇口，前唇口和后唇口均需要光顺。前唇口是指埋入式进气道唇口在深度方向处于最低点前的那一部分，后唇口则是指深度方向上的最低点与相贯线的后段点之间的那一部分。对前唇口光顺主要采用周向光滑不等距插值的方法。把进气道唇口所在范围内每个横向截面与外围的圆柱形面进行光滑过渡。对后唇口光顺则主要采用给定光顺半径规律进行内外型面的光滑过渡。

3进气道气动优化方案

3.1 优化方案气动设计

根据对进气道基础构型流场分析结论，确定了改变进气道进口位置、唇缘修型、中心线修改、面积率修改的优化方向。

首先，根据基础构型流场特征，第一优化方案将唇口位置整体前移，唇口捕获面积不变，进气道流道中心线相应改变、面积率改变，内流道相比基础构型整体略长。接下来，第二优化方案的设计中，在保持唇口位置、捕获面积不变条件下，进气道流道在扩张段下型面变化明显，曲率相比第一方案更加小，逆压梯度更加减小。

根据前两个方案数值模拟结果，经分析，依次调整面积率，并在扩张段上、下型线均做出相应优化设计，得到多组优化方案。优化策略是：通过部分方案的数值模拟评估，确认改变进气道哪些设计参数能够更加有效地提高进气道性能;接着，进一步开展优化设计，更加明确改变那些参数对提高性能更加有效;最后，设计了针对优先参数改变的优化构型，开展计算评估，优选得到进气道最佳优化构型。

3.2 优化方案数值模拟

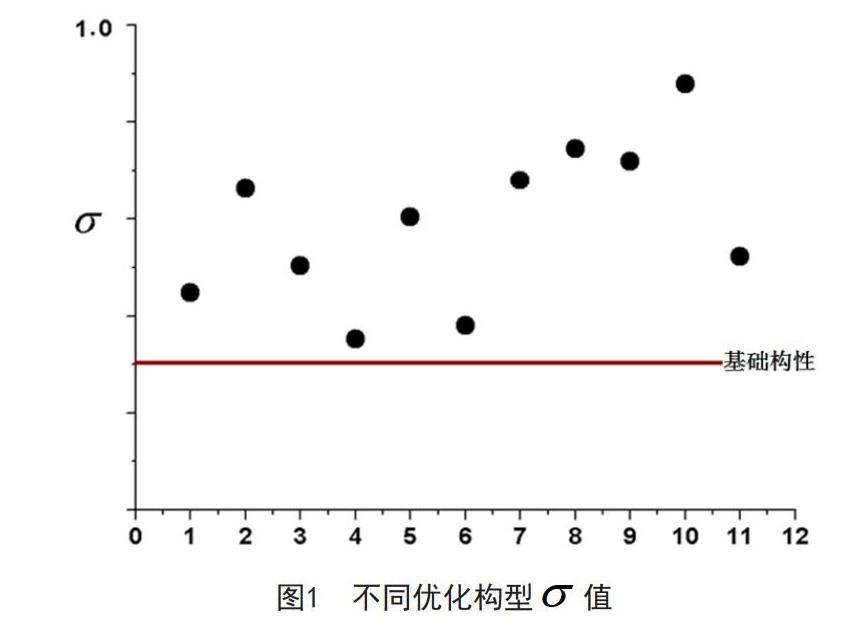
在进气道设计状态，数值模拟得到其总压恢复系数及流场畸变指标。图1、图2分别给出了进气道设计点、不同优化方案数值模拟得到的总压恢复系数及畸变指标曲线。

分析表明：在進气道设计点，最优构型数值模拟得到值相比基础方案提高1.4%。

4试验验证

分别以埋入式进气道基础构型、优化构型数模为基础加工试验模型，在中国航空工业空气动力研究院1.2米×1.2米风洞开展进气道试验。

试验内容为：针对两套进气道构型，首先在设计状态进行吹风试验，对比基础构型、优化构型气动特性，确定优选方案。选择优选方案，开展不同马赫数、不同姿态下进气道试验，获取性能数据和曲线。

5结束语

通过开展某埋入式进气道气动优化设计及试验研究，可得以下结论：

（1）通过对进气道基础构型数值模拟研究，明确了进气道部分区域存在流场分离，并造成进气道整体气动性能较差的基本流动机理。

（2）基于流动机理分析，通过调整进气道中心线、截面面积律、喉道及唇口设计参数，获得了11个进气道气动优化设计构型，通过数值模拟得到进气道优化构型，优化构型进气道总压恢复系数显著高于基础构型，畸变指标与基础构型基本一致。

（3）风洞试验结果表明，在进气道设计状态优化构型总压恢复系数显著高于基础构型，与基础构型相当;在其它流动状态，优化构型性能总体显著优于基础构型，二者畸变指标值相当。

参考文献

[1] Seddon J，Goldsmith E L . Intake aerodynamics[M]. American Institute of Aeronautics and Astronautics，1985：31.

[2] Tsay W， Chen C. Numerical simulation of the submerged inlet[R]. AIAA 90-2137， 1990.

[3] Seddon J，Goldsmith E L. Intake Aerodynamcs[M]. London： Blackwell Science，1999：219.

[4] Ferguson S D， Eastman D W. High performance submerged air inlet[P]. US：Patent 4378097，1983.

[5] 郭荣伟，刘少永. 埋入式进气道的设计[J].南京航空航天大学学报，2001，33（2）：8-12.

[6] 任三星. 埋入式进气道设计与流场控制研究[D].南京：南京航空航天大学，1993.

[7] John D. Anderson. Computational Fluid Dynamics[M].北京：清华大学出版社，2004：45-103.

[8] Taskinoglu E，Knight D . Numerical Analysis of Submerged Inlets[C].Aiaa Applied Aerodynamics Conference. 2013.

[9] Taskinoglu E S，Knight D. Design optimizationfor submerged inlets PartⅠ[R]. AIAA-2003-1247，2003.

[10] Taskinoglu E S，Knight D. Design optimizationfor submerged inlets PartⅡ[R]. AIAA-2003-3926，2003.

[11] Taskinoglu E S， Jovanovic V， Knight D. Multi-objective design optimization and experimental measurement for a submerged inlet[R]. AIAA-2004-0025，2004.

[12] Jovanovic V， Taskinoglu E S， Knight D. Experimental investigation of a submerged subsonic inlet[R]. AIAA-2004-2649，2004.

作者简介

赵振山（1980-），男，山东淄博人;毕业院校：航空研究院，专业：流体力学，学历：硕士研究生，高级工程师，现就职单位：中国航空工业空气动力研究院，研究方向：内流空气动力学。