利用点的投影弥补空间想象力的欠缺

姚洁　杜娟

摘 要：空间想象力是学会机械制图的基本条件，也是必要条件，在解决问题中，我们要善于巧妙利用点的投影的知识点来弥补空间想象李不足的情况，如果可以将点的投影规律与空间想象力相结合，经常多练多看多想，不仅可以帮助提高空间想象力。而且还能更快速地解决制图中一些较复杂的图形问题。

关键词：点的投影;空间想象力

职业类学校的学生本身学习基础较差，学习能力较弱，学习自觉性不够，而机械制图是一门对空间想象力要求较高的学科。空间想象力是学好制图的基本条件，也是必要条件。

很多同学看到图形大脑就一片空白，完全不知道从何下手，一直纠结于空间想象力的欠缺。殊不知，要想培养空间想象力，关键要加强投影规律的应用。点动成线，线动成面，面动成体，反之，则要想解决空间立体的三视图，就可以分解为平面图形的投影，而平面图形的投影则可以分解为线的投影，同样，线的投影还可以分解为点的投影。那么必须在熟练掌握投影规律的基础上，明确平面图形与空间立体之间的对应关系，明确每条线与空间立体之间的对应关系，明确每个点与空间立体之间的对应关系。

在机械制图中，我们所说的点，既没有大小，也没有形状，很抽象，但点的投影是线、面投影的基础，也是进一步认识立体投影规律的基础。有时候巧妙利用点的投影，可以帮助我们解决很多因为缺乏空间想象力而解决比较困难的难题。

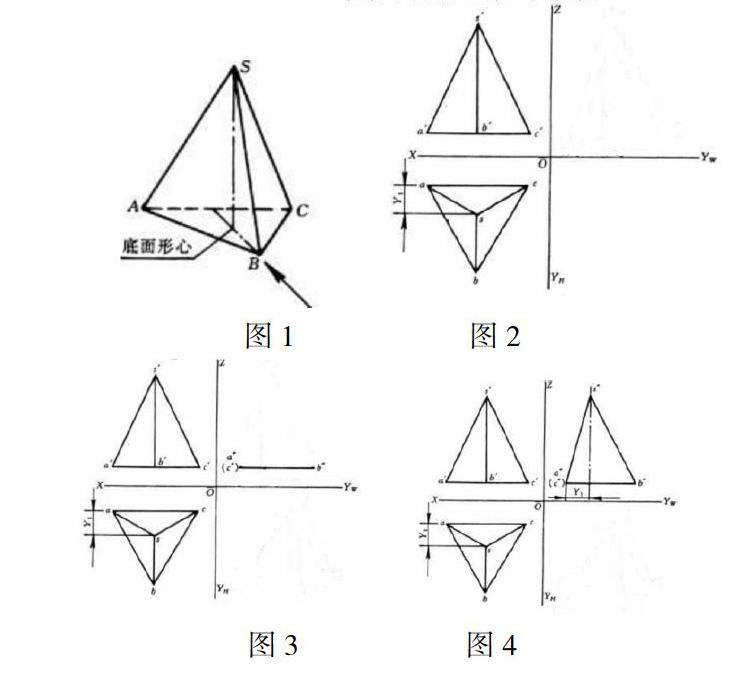
有一个很明显的例子，如要求绘制正三棱锥的三视图（正三棱锥如图1）。在课堂上，大家通过分析，正三棱锥是锥体中底面是等边三角形，三个侧面是全等的等腰三角形的三棱锥。正三棱锥不等同于正四面体，正四面体必须每个面都是全等的等边三角形，这个知识点应该是显而易见的。如果按照图1中箭头所指的方向规定为主视图投影的方向，则相应可以确定俯视图和左视图的投影方向。仔细观察，最反映结构特征的是俯视图的等边三角形，而主视图的等腰三角形也可以很快确定下来，如图2所示。当老师提问：大家想象一下，左视图是什么形状。這时，全班同学异口同声地回答：“等腰三角形！”可能这是绝大多数人都会犯的错误。事实上，正三棱锥两侧面之间的夹角不是90°，而主视图和左视图投影方向之间90°的夹角与之不相符，所以左视图的三角形肯定不是一个等腰三角形。那么左视图到底是一个什么形状的图形呢？这个问题让很多同学都很困惑，就算有较好的空间想象力，也无法凭空想象出它的形状，更无法准确地形容它的形状，那现在该怎么办呢？此刻点的投影规律的应用就可以大显身手了。

首先我们可以确定底面△ABC的三个顶点A、B、C在侧投影面上形成的投影a"、b"、c"所在的位置。通过画图发现A点和C点在侧面的投影a"和c"是重影点，再判断其可见性，a"为可见点，而c"为不可见点（如图3所示）。现在关键的问题就是顶点S所在的位置，它直接决定了这个三角形的形状。假如S点位于底边的中垂线上，则左视图为等腰三角形;假如S点偏离中垂线的位置，则左视图为一个任意三角形。接着我们可以继续利用点的投影规律，圆规截取俯视图中s点到线段ac的距离Y1，立刻就能确定顶点S在左视图上的投影s"所在的位置（如图4所示）。显然，正三棱锥的左视图为一个类似三角形。通过这道题，我们可以发现，当空间想象力无法解决问题，可以尝试着借助点的投影的知识点。

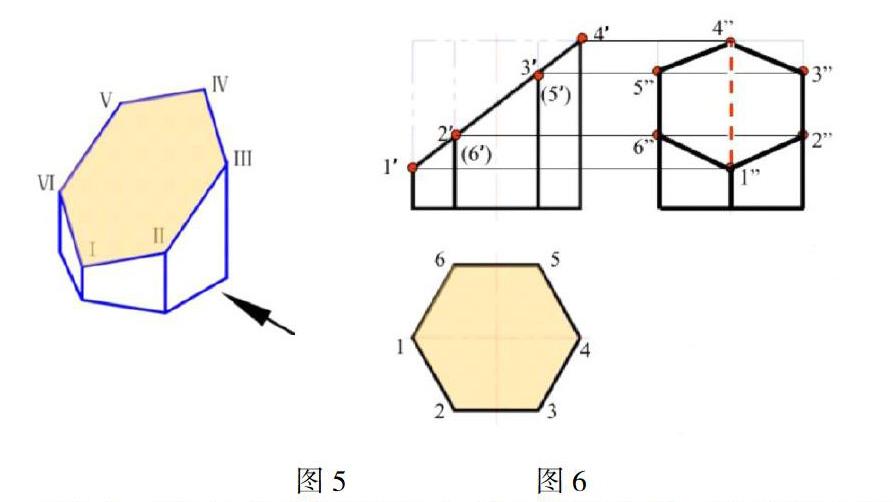
下面我们再举一个例子进行说明，如图5所示的正六棱柱被切割，利用点的投影绘制出截平面上点在左视图中的投影1"、2"、3"、4"、5"、6"（如图6所示），图形则一目了然了。

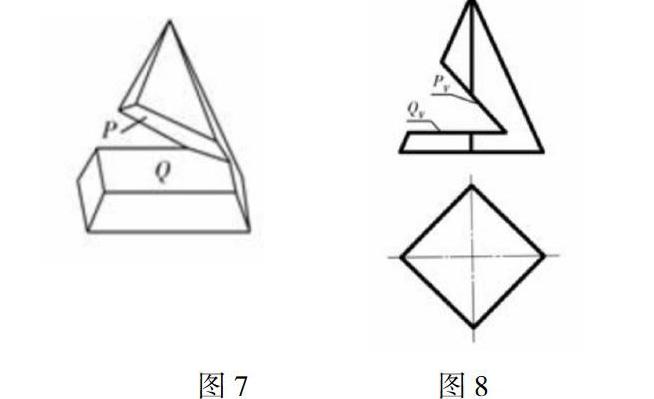
相比上一题正六棱柱被切割而言，这个题目（如图7所示）要复杂得多。首先观察模型并进行分析其形体结构，该正四棱锥分别被平面P、Q切割（如图8所示），如果仅凭学生现有的空间想象力似乎困难重重，但是能够有点的投影加以助力，那问题就能迎刃而解了。

首先，在正面投影上依次标出各侧棱与截平面的交点1′、2′、3′、4′、5′、6′、7′、8′。

其次，先求平面Q截四棱锥的截交线的投影。由1′在俯视图上求1，由1作四边形与底面四边形对应边平行可得2、5，平面Q与P的交线ⅢⅣ的投影可由3′、4′在俯视图上求得3、4;侧面投影1″、2″、3″、4″、5″可按投影关系直接求得。同理，可求出平面P截四棱锥的截交线的水平投影和侧面投影6、7、8和6″、7″、8″。

然后判别可见性，依次连接各点的同面投影。

最后进行整理，擦去多余的线，完成作图，如图9所示。

由以上几个例子，我们能明显感觉到点的投影规律的应用是普遍存在制图中的，特别是遇到一些较复杂的图形时，我们完全可以依赖于点的投影去解决一些较复杂的图形。而完成以后再由三视图想象出立体形状，经常这样反复地多画多看多想象，就可以慢慢培养空间想象力，