基于相关性方差贡献率的高坝泄洪振动数据级融合方法
马 斌,张 泽,赵 钊
(天津大学水利工程仿真与安全国家重点实验室,天津 300350)
随着拥有大库容及高泄洪能量的高拱坝及碾压混凝土坝[1]建设水平的快速提高,其数目亦越来越多,因而给予其更多的科学研究,保证其在受到泄洪激励时,泄流结构能够健康安全的运行是十分必要的。基于传感器振动响应进行坝体结构参数识别可有效诊断坝体的健康状态[2-7]。在进行关键部位测试时,单一传感器信号仅能反映结构的局部特性,且其测试结果容易受到环境背景噪声等外界因素的干扰,无法满足要求。因此,应在结构的不同位置布置多个传感器,并需要一种可以把不同测点的振动信号融合在一起的信息融合[8]方法,以提取出全面和准确的坝体动力信息。优选多传感器数据融合技术对结构进行安全监测和诊断是解决大型复杂结构健康运行评估问题的有效途径。
近年来,多传感器信息融合技术发展迅速[9-12],产生了诸如基于相关函数的数据级融合等方法[13-15]。本文提出了一种基于相关性方差贡献率的数据级融合方法,将该方法应用于锦屏一级高拱坝原型观测得到的拱圈测点振动位移信号数据融合和碾压混凝土重力坝水弹性模型实测信号的数据融合,并将融合结果与基于相关函数的数据级融合方法的结果进行了对比。
1 基于相关性方差贡献率的数据级融合方法
1.1 方法的提出
振型和工作频率是用以判断坝体结构健康程度的重要因素。作为最易获得的坝体参数,工作频率会随着坝高的增加而逐渐降低和密集[16-17]。大型泄流结构在受到高速水流冲击时,频率和能量不尽相同的振动响应会出现在结构各个部分。以往的多传感器数据级融合方法尽管能够在融合过程中准确识别部分响应的共有频率成分,然而也会造成一些有效信息的遗失。因此,选择有效的数据融合方法来进行高坝泄流结构测点振动信号的处理至关重要。具体而言,所采用的数据融合方法必须在能够对各个传感器的振动信号进行准确提取的同时,兼顾它们之间的互补性、冗余性及相关性。本文提出了一种基于相关性方差贡献率的数据级融合方法,该方法以方差贡献率为依据,以实测振动信号的重要程度来分配融合系数,完成多传感器信号之间的动态融合,进而可很好地防止有效信息的遗失。

图1 基于相关性方差贡献率的数据级融合算法的融合过程
1.2 基于相关性方差贡献率的数据级动态融合模式


(1)

(2)
式中:xi为定值或与时间相关;ki在传统数据级融合算法中为定值,在动态融合模式中依据某种原理随时间t而变化。
1.3 相关性方差贡献率的定义
假定r个传感器的测试信号分别为x1,t,x2,t,…,xr,t,第i个传感器与第j个传感器的信号xi,t、xj,t的互相关性为
(m=0,1,…,k(k≤N-1))
(3)
式中:m为信号作互相关计算时的时间坐标移动值;N为测试信号总的数据个数。
互相关计算得到的信号能量Eij的表达式为
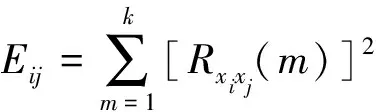
(4)
第i个传感器与其他所有传感器信号总的相关能量Ei为

(5)
进行能量归一化,获得单一传感器信号xi,t的能量归一化信号yi,t:

(6)
当有G个同质传感器在某一采样频率下一定时间内采集h个数据时,第g个传感器所采集到的数据信号序列为xg,1,xg,2,…,xg,h,其中第p个数据为xg,p,其能量归一化信号为yg,p,其方差贡献率为[18]
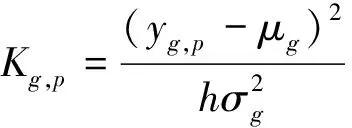
(7)
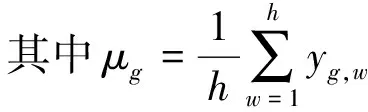

根据某一时刻不同传感器采集到的振动信号的方差贡献率,传感器g所采集到的第p个数据xg,p分配的融合系数kg,p为

(8)
则融合后p点的值xp为

(9)
基于相关性方差贡献率的数据级融合方法的融合过程见图1。
2 实测信号的数据融合检验
2.1 锦屏一级拱坝坝顶测点振动信号融合
锦屏一级拱坝坝高305 m,是世界已建第一高拱坝。锦屏一级拱坝共分为26个坝段,坝身设5个深孔、4个表孔,坝后接梯形断面水垫塘。沿坝顶2~24号坝段水平顺水流向,布设7个LFD-0.35-5-V(H)-WP型动位移传感器对坝顶水平动位移进行监测。从左坝肩至右坝肩测点依次为H1~H7,测点布置见图2。

图2 锦屏一级双曲拱坝坝顶动位移测点布置

图3 H1测点动位移响应
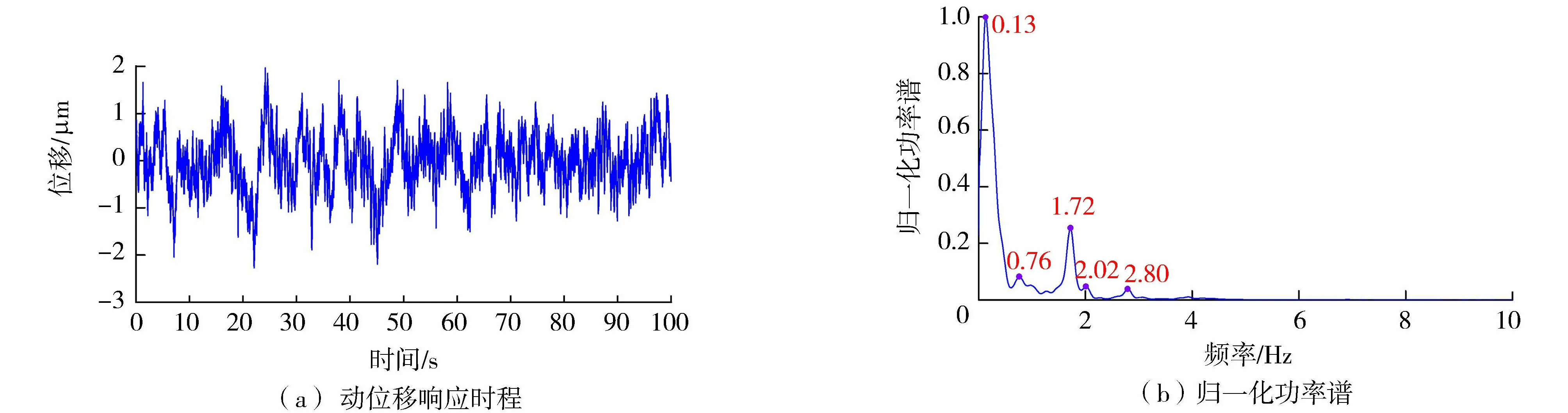
图4 H7测点动位移响应
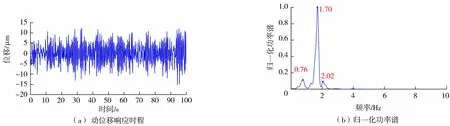
图5 H3测点动位移响应
在观测过程中,传感器采样频率采用200 Hz,采样时间为100 s。图3~5给出了3号表孔100%开度工况下H1、H7、H3测点的动位移响应时程和归一化功率谱。
从实测各测点的测量结果可以看出,在此种工况下,左右坝肩附近的测点测得的振动信号频率成分较多,且存在明显的白噪声(图3、图4)。布置在中间坝段的测点所采集到的信号主频在1.4~2.3 Hz,频率成分比较清晰(图5)。由此可见,传感器获得的信号频率随着泄流结构测点位置不同存在着明显差异,单个测点传感器采集的振动信号无法反映结构的整体振动特性。采用本文提出的基于相关性方差贡献率的数据级融合方法对H1~H7测点响应进行融合,得到其融合后的信号归一化功率谱如图6所示,采用基于相关函数的数据级融合方法得到的信号归一化功率谱如图7所示,两种方法融合结果对比如表1所示。

图6 基于相关性方差贡献率融合后信号归一化功率谱
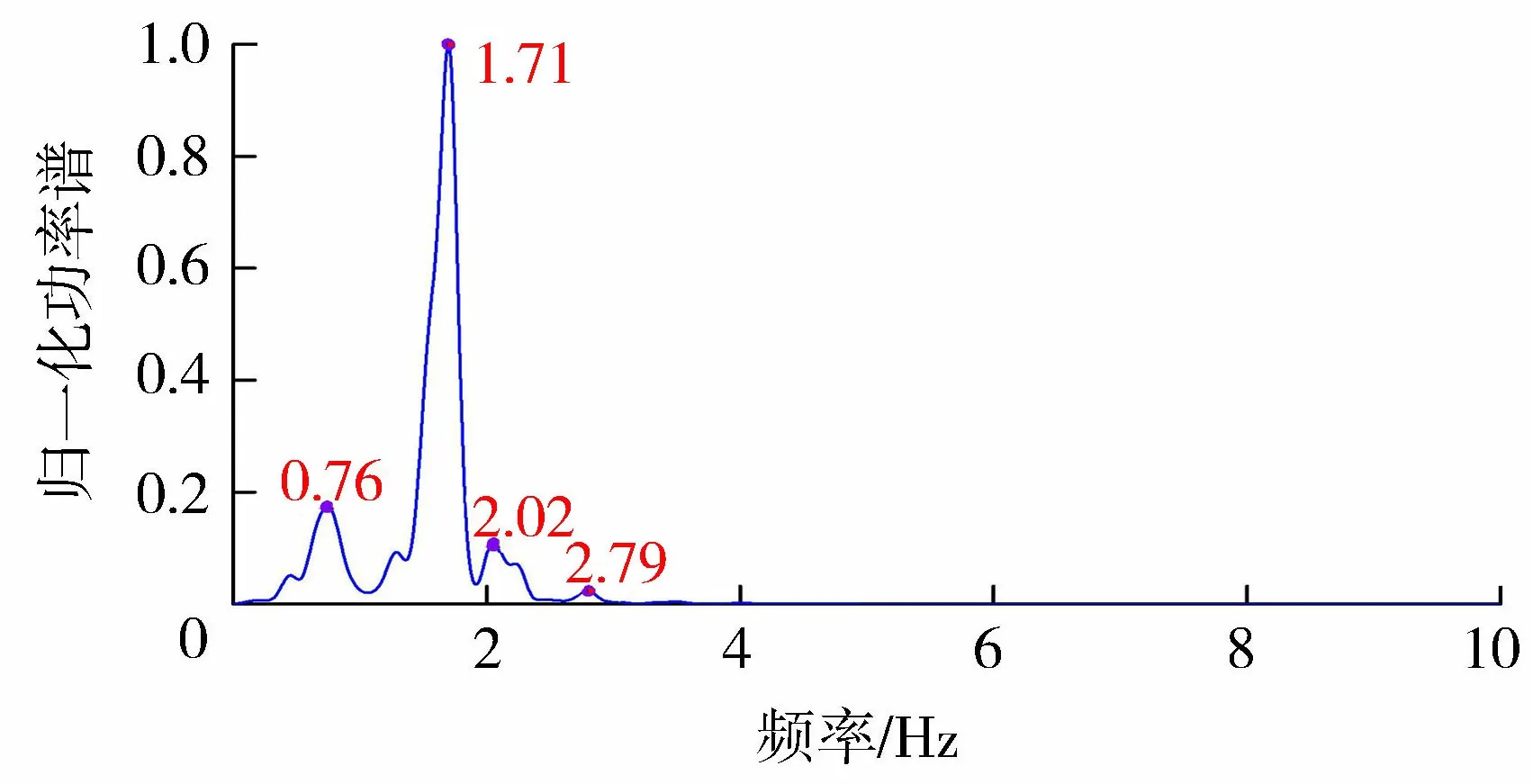
图7 基于相关函数融合后信号归一化功率谱
由表1可以看出,H1、H6、H7测点的坝体频率成分较为丰富,而H2、H3、H4、H5测点缺少坝体高频与低频信息。通过融合结果可以看出,基于相关函数融合后的信号仅含有4阶频率成分(0.76 Hz、1.71 Hz、2.02 Hz、2.79 Hz),丢失了高频与低频信息;而基于相关性方差贡献率的方法融合后的信号含有丰富的频率成分(0.12 Hz、0.41 Hz、0.76 Hz、1.72 Hz、1.98 Hz、2.25 Hz、2.81 Hz、3.11 Hz、3.37 Hz、3.94 Hz),说明该方法能够提取到完整的信号频率。由此可见,本文提出的基于相关性方差贡献率的数据级融合方法融合后的信号能够更全面地反映和体现高拱坝的整体动力特性,该方法有利于挖掘传感器振动信号中的高频微弱信息和密频信息。

表1 锦屏一级双曲拱坝振动位移信息融合结果
2.2 碾压混凝土重力坝水弹性模型流激振动信号融合
根据试验要求,模型比尺采用1∶300,按水弹性相似要求利用加重橡胶模拟带成层结构碾压混凝土坝,加重橡胶弹性模量为110 MPa,软弱夹层处的橡胶弹性模量为8.0 MPa。该模型分为非溢流坝段和溢流坝段,高74 cm,宽50 cm,闸墩高度11 cm。为准确获取带成层结构碾压混凝土坝流激振动响应信息,在建好的物理模型的左、右闸墩上分别布置1个顺水流方向的动位移传感器(测点X2、X3),左坝肩顺水向、横河向、竖向各布置1个位移传感器(测点X1、Y2、Z2),右坝肩顺水向、横河向、竖向各布置1个位移传感器(测点X4、Y1、Z1),传感器的布置见图8。采用中孔全关、上游水位380 m,单表孔开度22 m工况下测得的泄洪振动响应信号进行分析。图9、图10分别给出了X1、Y1测点的动位移响应。

图8 带成层的碾压混凝土坝水弹模型及位移传感器布置
从各个测点振动信号的归一化功率谱来看,碾压混凝土重力坝不同测点信号所含有的频率成分差异较大,单测点信号无法反映碾压混凝土重力坝整体的振动特性。利用本文提出的基于相关性方差贡献率的数据级融合方法融合各测点的振动信号,融合后的振动响应时程和归一化功率谱见图11。同时也采用基于相关函数的数据级融合方法融合各测点的振动信号,融合后的振动响应时程和归一化功率谱见图12。可以看出,基于相关性方差贡献率的融合方法结果含有更丰富的频率信息。此外,利用数值模拟的方法模拟该碾压混凝土重力坝的湿模态,其模型见图13,提取出数值模拟的前8阶模态信息与前两种数据融合方法结果进行比较。同时对该碾压混凝土坝进行模态测试,通过锤击法测定测点的时程信号,求解各测点的频响函数。利用锤击法进行的模态测试试验布置见图14,测出前8阶模态的模态频率,也与两种数据融合方法进行对比,对比结果见表2。

图9 X1测点动位移响应

图10 Y1测点动位移响应

图11 基于相关性方差贡献率融合的振动响应信息

图12 基于相关函数融合的振动响应信息

图13 重力坝流固耦合模型

图14 湿模态试验测点布置与仪器

表2 重力坝水弹性模型模态识别结果
从表2可以看出,基于相关性方差贡献率的数据级融合方法、锤击法、有限元数值模拟法3种方法识别结果较为接近,都能够较为准确地识别出碾压混凝土重力坝的前8阶模态,验证了本文提出的融合方法的准确性,同时也说明本文方法适用于碾压混凝土坝振动信号的模态参数识别。
3 结 语
基于高坝泄流振动响应特性,提出了基于相关性方差贡献率的数据级融合方法。该方法通过计算振动信号的相关性方差贡献率来分配融合系数,从而实现多传感器信号之间的数据融合。将该方法运用到锦屏一级高拱坝原观拱圈测点振动位移信号和碾压混凝土重力坝水弹性模型实测信号的数据融合中,结果表明该方法具有良好的抗噪性,有利于挖掘信号中的高频微弱信息和密频信息,可以完整地表现出坝体的整体动力特性。基于相关性方差贡献率的数据级融合方法、有限元数值模拟法、锤击法对碾压混凝土坝水弹性模型实测信号的识别结果较为接近,3种方法都可以对碾压混凝土坝前8阶模态进行精确识别,验证了本文方法的有效性,同时说明本文方法适用于高拱坝及碾压混凝土坝振动信号的模态参数识别。

