内孤立波环境下柱体的受力特性

王 寅，王玲玲，计 勇，席芝橙，张雯雯

(1.南昌工程学院水利与生态工程学院，江西 南昌 330099; 2.河海大学水利水电学院，江苏 南京 210098)

内波通常发生于密度稳定分层的水体内部[1]。在海洋、河口、湖泊等流体系统中，温度、盐度以及其他环境因素引起的密度沿水深方向上的改变，会导致水体密度的分层[2]。在此类环境中，微弱的外界扰动就可能在密度分界面(密度跃层)上引发携带巨大能量的内波现象。内孤立波是一种特殊的非线性内波，其振幅大、周期短、所携能量大[3]，大振幅内孤立波对近岸及河口复杂水动力环境中工程结构物的安全稳定性有非常大的影响[4]。内孤立波在传播过程中以密度跃层为界上下水层呈反向流动，由此产生的剪切流所携带的巨大能量会导致异常强大的流速。内孤立波2.1m/s波致流作用下的柱体所承受的最大荷载相当于波长300 m、波高达到18 m的表面波作用[5]，这种强烈的作用力可能对近岸及河口复杂水动力环境中水下立管及水下支撑桩柱的安全稳定性造成严重的威胁[6]。深入研究内孤立波对水下结构物的作用机理以及结构物内波动力学问题具有非常重要的工程应用价值。

柱体所受水平力可分为压差阻力和摩擦阻力两部分[7]。压差阻力是由于柱体迎流面和背流面的压差所产生的水平力；摩擦阻力是由于流体黏性作用所产生的水平力，即黏滞力。以往受力研究多只计算出内孤立波对柱体的整体作用力[8-10]，并未考虑在不同分层水体中柱体不同部分受力随水深分布情况，因此并不能获知柱体详尽的受力特性。本文借助三维数值波浪水槽，采用大涡模拟(large-eddy simulation，LES)技术模拟内孤立波的产生和传播，通过提取数模计算结果中不同水层柱体表层的压强分布及切向速度，采用微元法积分出柱体在各水层所受压差阻力以及黏滞力，由此获取受力沿水深分布特性，以揭示分层流环境下柱体的受力机理。

1 控制方程及求解方法

1.1 动量输运方程

基于连续性假设，可用Navier-Stokes方程(N-S方程)描述不可压缩黏性流体三维瞬态运动过程：

(1)

(i，j=1，2，3)

(2)

式中：ρ为密度项；t为时间；xi、xj为笛卡尔坐标系的3个方向坐标；ui、uj为笛卡尔坐标系中的3个流速分量；p为压力项；μ为动力黏性系数；fi为i方向的单位体积力。

1.2 标量输运方程

采用考虑了两层水体之间的质量交换作用以及对流-扩散影响的标量输运方程：

(3)

ρ=C+ρ0

(4)

式中：C为盐度，kg/m3；k为分子扩散系数；S为源项；ρ0为清水密度，kg/m3。

1.3 大涡模拟

大涡模拟技术是对紊流脉动的一种空间平均，通过滤波函数将大尺度的涡和小尺度的涡分离开[11-14]。过滤后的动量和质量方程可表示为

(5)

(6)

(7)

1.4 柱体压差阻力的求解方法

1.4.1圆柱

如图1所示，P为水深为y的截面圆柱表面上受到的点压强(基于数值模拟结果提取)，则该截面圆周所受水平方向的压差阻力fc可定义为

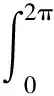
(8)

式中：θ为点压强P与x轴的夹角，(°)，以逆时针为正；l为弧长，cm。

图1 圆柱压差阻力计算方法示意图

基于微元法，可将式(8)离散为

(9)

式中：Pi为作用在第i个微元上的压力，Pa；θi为第i个微元法线延长线与x轴的夹角，(°)，以逆时针为正；n为圆周被等分数，本文取n=360；Δli为第i个微元的弧长,Δli=2πr/n=0.087 cm(r为圆柱半径，本文取r=5 cm)。

1.4.2方柱

如图2所示，假定水深为y的截面方柱表面上受到的点压强为P，则该方柱截面所受水平压差阻力fs定义为

(10)

式中：fsj为作用在方柱截面第j(j=1，2，3，4)条边上的压力，N；Pi为方柱各边第i个微元上的压力，N；Δsi为第i个微元的边长，Δsi=4s/m=0.11 cm(s为方柱周长，本文取s=10 cm;m为方柱周长被等分数，本文取m=360)。

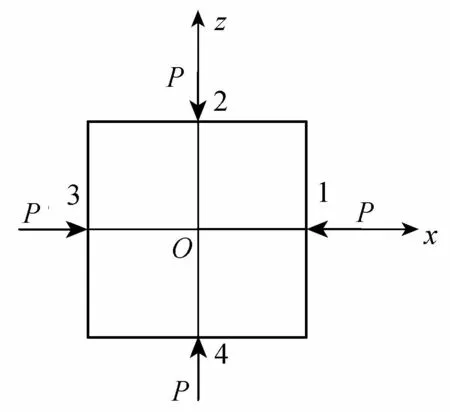
图2 方柱压差阻力的计算方法示意图

1.5 柱体黏滞力的求解方法

1.5.1圆柱

如图3所示，可将距离圆柱表面最近一层网格上某微元a的切向速度uτ和径向速度uγ(基于数值模拟结果提取)定义为

uτ=uzcosθ-uxsinθ

(11)

uγ=uzsinθ+uxcosθ

(12)

式中：ux、uz分别为该微元的x方向和z方向速度，cm/s；θ为微元a与x轴的夹角，(°)，以逆时针为正。则某微元i所受水平方向上的黏滞力Δfcτi为

(13)

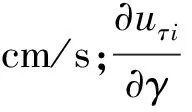
图3 圆柱黏滞力计算方法示意图

基于微元法，圆柱表面所受水平方向上的黏滞力fcτ为

(14)

1.5.2方柱

如图4所示，沿用上述圆柱黏滞力的计算方法，可求得水深为y的截面方柱表面所受水平方向上的黏滞力fsτ：

图4 方柱黏滞力计算方法示意图

(15)

其中

2 数学模型

建立三维数值波浪水槽如图5所示，水槽长12 m、宽0.6 m、高0.8 m，柱体周围水平网格和水槽垂向网格划分方法如图6、图7所示。

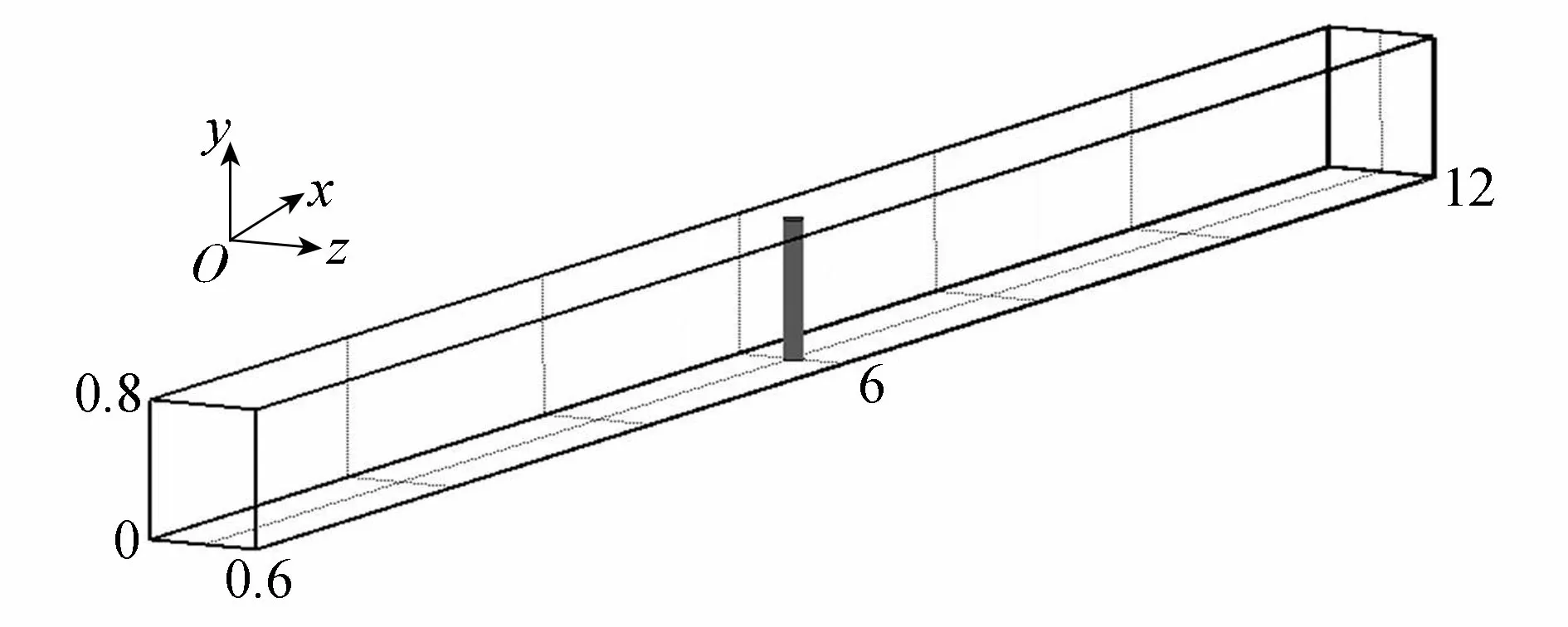
图5 三维数值波浪水槽示意图(单位：m)

图6 柱体周围水平网格划分方法

图7 垂向网格划分方法

定义在数值模拟中柱体所受的无量纲水平合力F′的计算公式[15]为

(16)

图8 不同波幅时柱体的F′随时间t的变化过程

式中：F为数值模拟中计算所得的柱体所受水平力合力，N；A为柱体的迎风面积，cm2；H为水槽总水深，cm；g为重力加速度，m/s2。

2.1 计算工况

数值模拟采用的波形为下凹型，参数设定及工况选定具体为：上层为清水，密度ρ1=0.998 g/cm3，水层厚度h1=0.2 m；下层为盐水，密度ρ2=1.017 g/cm3，水层厚度h2=0.6 m，总水深H=0.8 m，设定4种工况N1、N2、N3、N4，相对波幅ηo/H分别为0.026、0.044、0.054和0.098。如图9所示，采用重力塌陷法制造内孤立波[16]，图中造波区两侧密度跃层高度差ho称为阶跃高度，造波区长度Lo称为阶跃长度。

图9 重力塌陷法造波示意图

2.2 数值模拟方法和边界条件

三维数值波浪水槽中下凹型内孤立波的形成和传播采用大涡模拟技术模拟；利用SIMPLE算法对流速-压力项进行耦合，以保证质量守恒，并由此得到压力场；利用二阶中心差分格式及隐式格式分别对空间和时间进行离散。造波区端边(图9中的左边壁)、数值水槽底部以及柱体壁面均采用无滑移固壁边界，水槽两侧采用滑移固壁边界。为了使内波不发生反射，水槽右端采用Sommerfeld辐射型边界[17]；顶部采用“刚盖”假定，以此忽略表面波的影响[17]。

2.3 数学模型验证

采用与文献[18-19]相同的方法验证了建立的数学模型，比较了不同波幅情况下，圆柱和方柱模型试验与数值模拟中内孤立波作用力的时历曲线。结果表明模型试验与数值模拟结果吻合较好，验证了建立的数学模型的可靠性，可用于后续试验的模拟。

3 模拟结果与分析

内孤立波环境下的速度场和压力场与密度均一流环境区别较大，在内孤立波作用下柱体受力三维特性更加明显[18]。准确剖析柱周流场及柱表压强分布是科学研究和预测近岸及河口地区桩柱受力的必要条件。柱体所受水平力可分为压差阻力和摩擦阻力(黏滞力)两部分，这两类力求解的基本思路：①在柱身沿垂直(y)方向每隔一定距离截取1个断面，基于模拟结果在每个断面上沿柱周向选取360个点，并提取这些点的压强值及流速值(得到柱周的压强分布及流速分布)；②采用微元法，通过积分不同断面柱周的压强分布和流速分布可分别得到圆柱及方柱的压差阻力f(式(9)(10))和黏滞力fτ(式(14)(15))。

3.1 柱体压差阻力沿水深的分布

定义柱体在水深y处所受无量纲水平压差阻力f′为

(17)

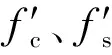
3.2 柱体黏滞力沿水深的分布

(18)

表1 圆柱和方柱的无量纲化水平压差阻力

3.3 单柱受力的量化分析

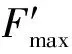
表2 柱体受力量化分析工况设置及相关参数

(19)

m=-0.88h1/h2+3.72η0/H+0.34

(20)

(21)

此时R2=0.957，拟合优度高(图10)。综合影响系数m虽是拟合过程中得到的，但其具有一定的物理意义：内孤立波相对波幅越大、上下水层厚度差距越大，则m值越大，对应柱体受力越大。m为两参数η0/H和h1/h2对柱体受力的影响提供了量化的指标，且m与η0/H正相关，与h1/h2负相关(式(20))。综上可知，柱体受力在不同分层条件下均随相对波幅η0/H的增大而增大；而在同一波幅条件下，水深比h1/h2越大，柱体受力越小。

图与ηo/H和h1/h2的相关关系

4 结 论

a. 波幅相同时，以密度跃层为界，方柱于上下水层中所受到的压差阻力均大于圆柱：上层水体中方柱受力约为圆柱的1.5倍；下层水体中方柱受力约为圆柱的3.5倍。

b. 作用于柱体上的黏滞力比压差阻力小1或2个数量级，因此可忽略流体的黏性效应，只考虑压差阻力的作用效果。

c. 受力峰值系数与相对波幅及水深比具有较强的相关性，且与综合影响参数呈明显的指数分布关系，两者拟合优度为0.957，拟合优度高。受力峰值系数与相对波幅正相关，与水深比负相关。