基于螺旋式电容传感器的生物质含水量测量
李云龙, 燕德国, 邓永强, 张文彪, 韩晓娟
(1.大唐长山热电厂, 吉林 松原 138000; 2.华北电力大学 控制科学与计算机工程学院, 北京 102206)
0 引言
生物质能源因其可再生以及碳中性的特点,在我国能源系统中占据着越来越重要的地位[1],[2]。生物质燃料的特性分析是生物质能源利用过程的重要参考依据。 在生物质燃料发电过程中,生物质燃料的含水量不仅影响电厂机组的发电效率,还影响电厂生产过程的安全性,因此,对生物质燃料含水量的快速测量具有十分重要的意义。
目前,已有多种技术相对成熟的生物质含水量的测量方法被应用于各个领域。 总的来说,这些方法主要分为两大类,即直接法和间接法[3]~[5]。直接法包括干燥法和化学法,这类方法具有原理简单、测量精度较高和不易受外界环境影响的优点,但是,也具有破坏性较大和耗时较长的缺点,不适合大规模使用,通常是在实验室环境下完成的,因此,这类方法常被作为获取标准值的参考方法。 间接法包括电学法、电磁法、近红外光谱法(NIR)和X 射线法等,间接法一般具有操作简单、快速、破坏性小和重复性好等优点,但是,测量精度易受外部环境和样本特性的影响,须要进行不断的改进和优化[6]。
电学法作为间接法的一个主要分支,在生物质含水量测量方面得到了一定的应用。 Mizukami Y 基于电阻和电容值估计了茶叶的含水量, 并开发了一个同时含有阻抗和电容的新模型, 该模型的测量精度较高,但是,容易受到叶片成熟度的影响[7]。Solar M 为了无损测定榛子的含水量,分析了电容、 介电常数等8 种电学参数随榛子含水量的变化趋势, 根据逐步多元回归分析建立的计算模型实现了榛子含水量的高精度预测, 该方法不须要破坏榛子的结构,具有成本低和非侵入的优点[8]。Kandala C V 通过测量平行板电容器在两个频率下的电容和相角,得出了一个经验方程,并以此来估计粮食作物的含水量,该方法具有检测速度快、测量精度高和样本可以重复使用的优点, 但是只适用于小样本[9]。当待测样品的含水量分布得不均匀时,单一电容传感器只能求得含水量的平均值,并不能提供关于样品含水量不均匀性的任何信息[10]~[12]。 上述研究都是基于普通的平行板电容器,由于平行板电容器的“边缘效应”,会导致传感器的灵敏度下降和非线性增强, 影响最终的测量精度。因此,如何获得更精确的测量结果还须进一步研究。
本文将采用一种螺旋结构的电容传感器 (简称螺旋式电容传感器) 对生物质的含水量进行测量。相比于平行板电容器,螺旋式电容传感器的灵敏度分布均匀,被广泛应用于过程参数的检测,而且该种传感器还可以克服生物质水分分布不均匀的问题[13]~[15]。 本文首先利用有限元方法对螺旋式电容传感器的结构进行优化,然后根据优化结果搭建相应的测量系统,最后对测量系统的准确性进行验证。 本文提出的螺旋式电容传感器可以实现生物质含水量的快速准确测量,将为生物质燃料的高效安全利用提供保障。
1 生物质含水量的测量
在实际应用过程中,平行板电容器会由于“边缘效应”导致传感器的灵敏度均匀性下降和非线性增加。 螺旋式电容传感器由不同角度的平行板电容叠加而成,其灵敏度均匀性有较为明显的改善。 通过对螺旋式电容传感器的结构参数进行优化,可以有效减小由于生物质堆积情况不同和生物质水分分布不均对测量结果造成的影响。
1.1 测量原理
随着生物质含水量(MC)的变化,样本的介电常数会发生相应改变, 从而引起传感器的电容(C)发生变化;建立生物质含水量与电容的数学模型后,就可以通过对生物质电容的测量实现对生物质含水量的预测。
1.2 传感器的结构
螺旋式电容传感器的结构如图1 所示。 从图1 可以看出, 传感器主要由检测极板和激励极板构成,为减小电磁干扰和提高灵敏度,传感器两端设置了两个环形的屏蔽接地电极。
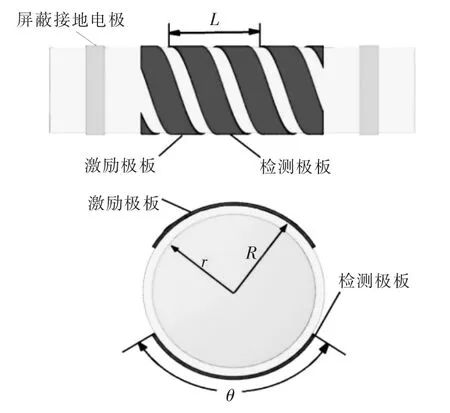
图1 螺旋式电容传感器的结构Fig.1 Structure of the helical capacitance sensor
图1 中:θ 为传感器极板的张角;r 和 R 分别为管道内径和外径。 极板在管道上的旋转角度也是一个很重要的参数,用极板旋转一周(360°)的轴向长度L 来表征。 本文所用管道的r=23 mm,R=25 mm。为了确定传感器的结构,本文主要优化极板张角θ、 极板旋转一周的轴向长度L 和极板旋转的圈数s。 为了方便研究,将每个待优化的参数均分为 4 个水平进行实验:θ 分别为 90,110,130,150 °;L 分 别 为 0.1,0.15,0.2,0.3 m;s分别为 1,1.25,1.5,1.75。
1.3 优化指标
本文基于有限元方法对不同结构传感器的灵敏度分布进行优化, 将测量区域分割成很多小单元,通过对每个单元建立公式进行求解,从而得到整个区域的解。 传感器灵敏度的计算式为
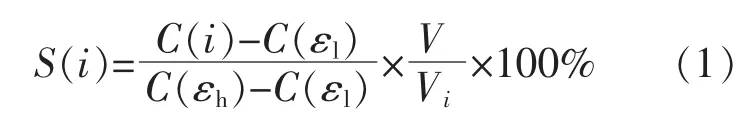
式中:S(i)为传感器的灵敏度;C(i)为 传 感 器 的电容,F;C(εl)为测量区域的介质全为空气时,传感器的电容,F;C(εh)为测量区域的介质全为水时, 传感器的电容,F;V 和Vi分别为整个测量区域和第i 个区域的体积,m3。
为了方便描述传感器灵敏度的均匀性, 将Sr作为表征传感器灵敏度分布均匀性的指标,Sr越小,传感器的灵敏度分布越均匀。

式中:Sσ为每个测量区域灵敏度的标准差;为测量单元的灵敏度的平均值。
1.4 仿真优化结果
采用正交试验设计的方法对螺旋式电容传感器的结构进行优化。 通过正交性从全面试验中挑选出部分有代表性的点进行正交试验, 从而以尽量少的试验, 获得足够多的有效信息。 基于COMSOL 软件对螺旋式电容传感器的结构进行建模仿真。 在激励极板上施加1 V 的电压,通过求解检测极板表面的电荷量进而求得电容。 正交试验的设计及结果见表1。 从表1 中可以看出,第8组参数所对应的Sr最小, 即对应的传感器的灵敏度均匀性最好。 因此,将 θ=110 °,L=0.3 m,s=1.25 作为最终的优化结果。

表1 正交试验设计及结果Table 1 Orthogonal table and simulation results
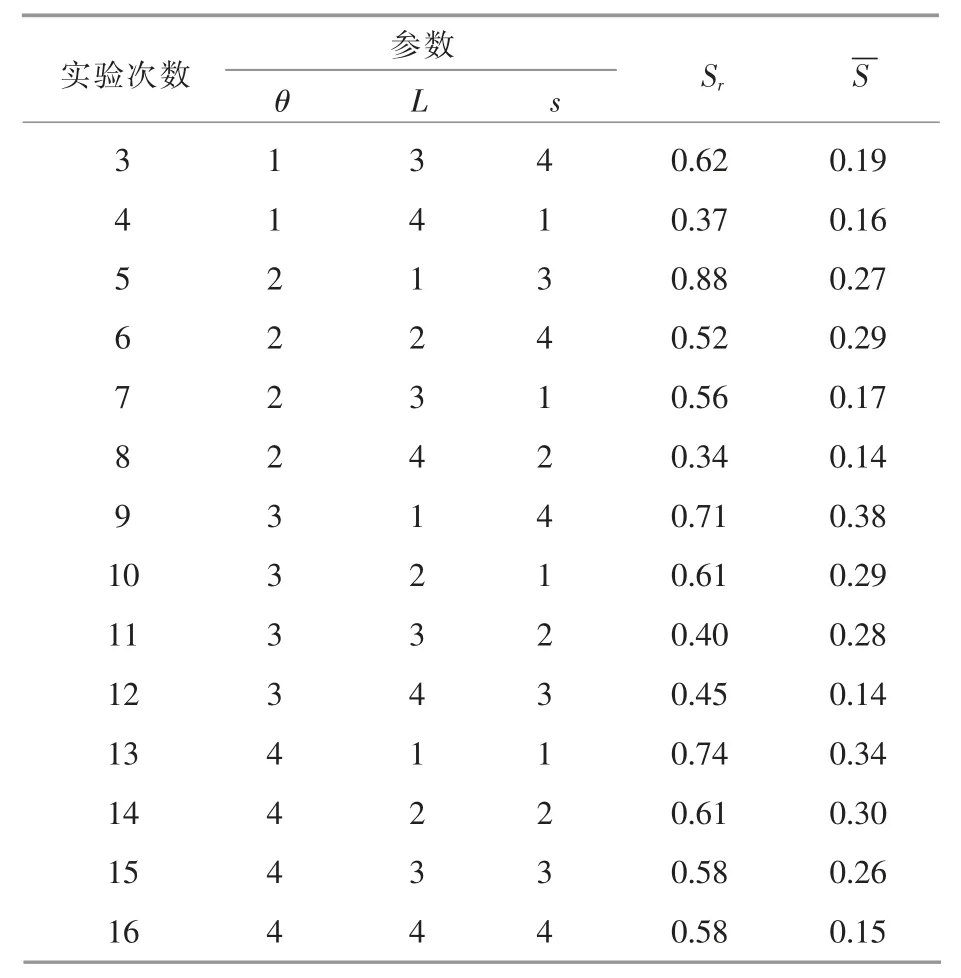
续表1
2 试验装置
2.1 木片样本的制备
本研究分别选择粒径为0.5 cm 和1.5~2.5 cm 的苹果树木片(徐州德英农产品公司)作为研究对象。 首先进行样本的制备,样本的初始含水量为12%,预期制备含水量分别约为12%,20%,28%,35%,42%和 48%的 6 组样本。 将每个粒径下的木片分成6 组,分别放在塑料瓶中,根据计算好的水量在每组样本中用小喷壶均匀喷入适量的水,静置并定期旋转塑料瓶,确保样本中的水分分布较为均匀。 静置一周之后,在每组样本中分别随机取3 组子样本, 并用Mettler Toledo HE83 型标准水分测定仪测定其含水量, 取3 组测定结果的平均值作为该组样本的标准含水量。最终得到粒径为0.5 cm 的样本的含水量分别为13.46% ,22.05% ,27.82% ,35.95% ,41.02% 和48.54%,粒径为1.5~2.5 cm 的样本的含水量分别为 12.95%,19.11%,28.86%,36.43%,43.18%和48.23%。
2.2 测量系统
本文搭建的测量系统如图2 所示。 在试验过程中, 将一定含水量的样本放入电容器中,轻轻摇动,保证传感器两极板间的空间填满样本, 用 Keysight E4980AL 型 LCR 表扫频记录螺旋式电容传感器在不同频率下的电学参数。

图2 测量系统Fig.2 The measurement system
3 结果与讨论
3.1 频率特性分析
对两种粒径的样本分别施加频率为2×104~2×106Hz 的激励信号, 测得不同含水量样本的电容随频率的变化情况如图3 所示。
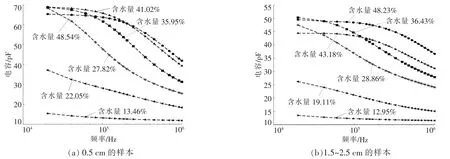
图3 不同粒径和含水量样本的电容随频率的变化情况Fig.3 Capacitance values of samples with different particle sizes and moisture content under different frequencies
从图3 可以看出, 不同含水量样本的电容均会随着频率的增大而减小, 且两种粒径样本的变化趋势基本一致。 当激励信号的频率为1×105~3×105Hz 时,样本电容随着频率的增加而下降的趋势较为明显。 当激励信号的频率接近于106Hz 时,样本电容的变化趋于平缓,并渐渐趋近于一个固定值。同时发现,在同一频率下,样本的介电常数会随着样本含水量的增大而增大,对应的电容也相应增大。 这是因为完全干燥的样本可以等效为绝缘体,而水作为一种极性物质,具有较大的介电常数,当样本的含水量较高时,介质等效的介电常数也会随之增大, 从而引起样本电容的增大。 此外,通过对比图3(a),(b)可以发现,当样本的含水量相近时,粒径为0.5 cm 的样本的电容大于粒径为1.5~2.5 cm 的样本对应的电容。这是因为相比于小粒径的样本,粒径较大的样本的堆积密度较小, 即空隙率较大,因此,等效的介电常数较小,对应的电容也较小。
3.2 样本含水量与电学参数之间的模型
从图3 还可以看出,在低频段,样本电容容易受到外界电磁的干扰, 传感器极板引线分布电容也会造成所得样本电容的波动。 随着激励信号频率的增大,样本电容趋于稳定,因此,选择在106Hz 的频率下建立样本含水量与电容之间的对应模型。
两种粒径样本的含水量与电容之间的关系如图4 所示。 从图4 可以看出,不同粒径样本的含水量与电容的变化趋势基本保持一致。 通过观察样本含水量与电容的对应关系, 分别采用一阶线性模型和对数模型对其进行拟合, 拟合结果如图4所示。
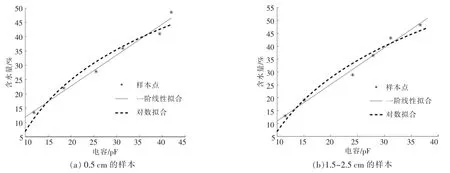
图4 不同粒径样本的含水量与电容之间的拟合曲线Fig.4 Fitting curves between water content and capacitance of samples with different particle sizes
在实际应用过程中,单一参数拟合模型的精度和可靠性达不到要求。Mizukami Y 在研究茶叶的电学参数与含水量之间的关系时,通过引入阻抗参数(Z),建立了一个同时利用 Z 和C 的多参数模型来预测茶叶的含水量,该模型的预测精度很高。

式中:A,B 均为常数。
本文利用上述多参数模型对106Hz 频率下两种粒径样本的阻抗参数、电容和含水量进行拟合,得到如图5 所示的曲线。
3 种模型的拟合结果如表2 所示。 表2 中:SSE 为和方差,SSE 越接近于0, 说明模型的拟合效果越好;R2为确定系数, 表征拟合的近似程度,R2的值越接近于1,说明方程的拟合效果越好。
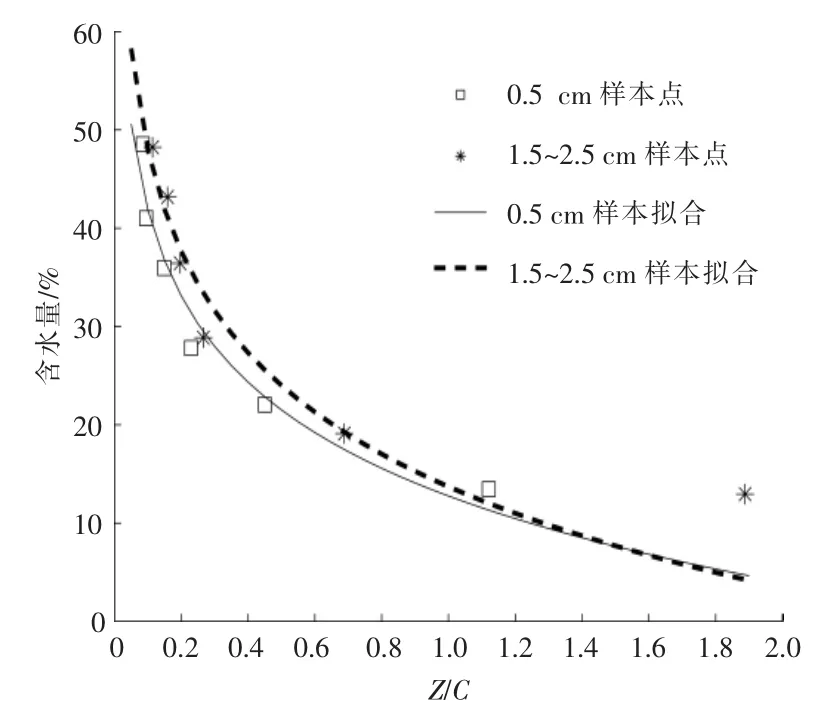
图5 MC=Aln(Z/C)+B 模型的拟合曲线Fig.5 Fitting results of MC=Aln(Z/C)+B
从图4,5 和表2 中可以发现:虽然两种粒径样本的含水量与电容的关系曲线的变化趋势相近,但是,由于不同粒径样本的空隙率不同,所以不同粒径样本的模型参数仍有差异;不同粒径样本的多参数模型的参数变化较小,即多参数模型对样本粒径的变化不敏感。通过对比3 种模型的SSE 和R2发现,相比于对数模型和多参数模型,一阶线性模型的SSE 较小,拟合精度较高。

表2 拟合结果Table 2 Fitting results
3.3 模型验证
为了进一步验证拟合模型的预测结果, 制备了含水量分别为26.88%,37.73%和44.20%的粒径为0.5 cm 的样本和含水量分别为32.38%,34.34%和41.64%的粒径为1.5~2.5 cm 的样本进行验证试验,结果如表3 所示。 表3 中:实际值为通过标准水分测定仪测定的样本含水量; 预测值为通过测量电学参数利用所得模型求得的样本含水量; 模型1 为一阶线性模型, 模型2 为对数模型,模型3 为多参数模型。
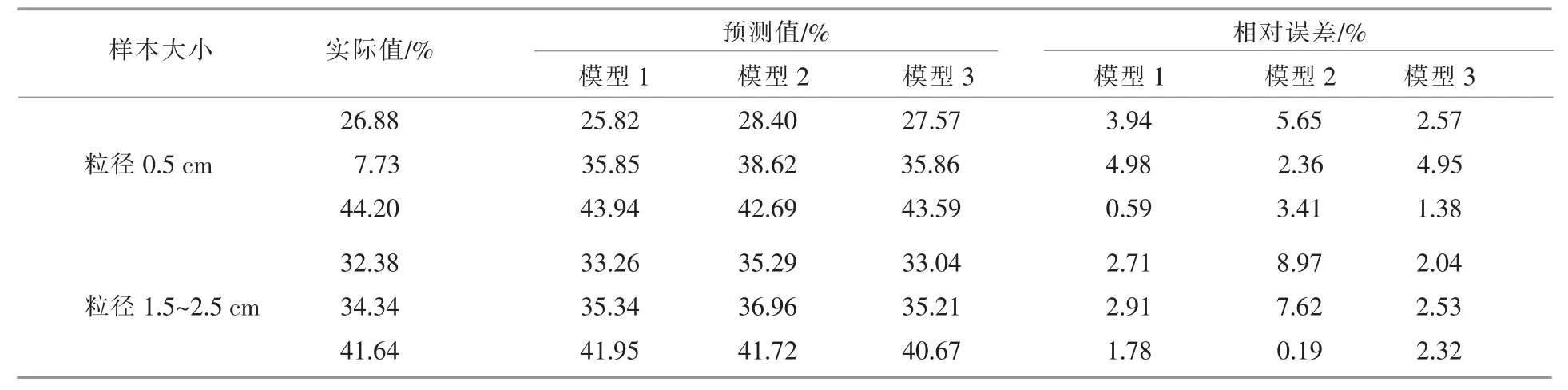
表3 模型验证结果Table 3 Model verification result
综合图4 和表3 可以看出, 当样本含水量为12%~48%时,样本电容与含水量具有一阶线性关系, 一阶线性模型和多参数模型预测得到的样本含水量的最大相对误差在5%以内。 由于不同粒径的样本在传感器中的堆积情况不同, 导致其空隙率不同,介电常数分布存在差异,从而影响所测电容的大小,导致对应的预测精度存在差异。
4 结论
生物质的含水量会影响其介电特性, 通过实验发现木片的含水量与其对应的电容之间存在很好的线性相关性, 可以通过这两者之间的关系来实现对生物质水分含量的预测, 本文所建立的一阶线性模型和多参数模型预测得到的样本含水量的最大相对误差在5%以内。 不同粒径对应的模型参数存在差异, 说明生物质粒径的差异会对模型预测结果造成影响。 通过对比两种粒径样本的模型可以发现, 多参数模型在不同粒径下的参数很相近, 说明多参数的拟合可以补偿由于粒径不同引起的传感器内空隙率分布差异对预测结果造成的影响。 同时,环境温度、湿度等外界因素也会对预测结果造成影响, 在今后研究中可以尝试建立多种电学和环境参数的统计或机器学习模型以实现更为准确的生物质含水量测量。

