多故障并发下考虑部件经济相关性的串并联系统选择性维护决策方法研究①
管业勤, 蒋祖华, 孙小明, 王海丽
(上海交通大学机械与动力工程学院,上海 200240)
0 引 言
随着中国制造2025进程的不断发展,设备的大型化、高性能化与自动化水平节节升高,因此维护成本对公司竞争能力的影响增加,维护策略优化越来越受到重视[1]。传统的维护策略研究大多假设设备因故障而停机后能迅速通过小修恢复[2],而实际生产中,由于设备结构、功能日趋复杂,设备故障的并发现象增多,设备失效后的维修决策需要考虑维修资源的约束。
以往适用于设备计划性停机的预防性维护策略[3]因较少考虑维修资源约束,不太适用于设备多故障并发下的非计划性停机情境。而以有限的维护资源为已知约束条件的选择性维护策略非常契合复杂设备多故障并发下的维修决策需求。
选择性维护的概念最早由Rice et al[4]提出,表示在维修资源(如维修时间、费用、器材、人员等)约束下,从一系列待修项目中确定所要实施的维修项目的过程,后经Maillart et al[5], Schneider et al[6]等人将其拓展至复杂系统的维修决策中。系统在实际运行中,可以处于完全失效和性能最优之间多个状态,因此对部件的维护方式有多种选择,不同维修方式可将其恢复至不同的状态。Pandey et al[7,8]等人将多种失效模式以及非完美维护与选择性维护模型相结合,研究了部件状态转移概率服从指数分布的串并联系统的选择性维护问题。Chen et al[9]以多状态系统为研究对象,建立可靠性约束下最小化维护成本的选择性维护模型。
选择性维护模型按目标不同可分为三类:(1)以最大化系统可靠性为目标,时间和费用等维修资源为约束[10];(2)最小化总维护成本,系统运行可靠度要求和维修时间为约束[11];(3)最小化总的维修时间,系统运行可靠度要求为约束[12]。
选择性维护方案通常是在多组件系统中实施许多维护操作,需要考虑部件之间的维修相关性,而部件间的经济相关性代表了一类最典型的维修相关性。经济相关性意味着若干个部件进行联合维护或维修时相比于单独维修或维护时的维修成本会节省。维修成本中包括停机成本、备件工具成本及人力成本等。Dekker et al[13]总结了成组维护中装配成本的节约在选择性维护中的应用,Nourelfath、Chatelet[14]研究了并联生产系统中部件间的经济相关性和结构相关性。文献[15]研究了串联系统在计划停机和非计划停机两种情境下的考虑经济相关性的选择性维护策略,文献[16-18]对计划停机下考虑经济相关性的串并联系统展开研究。
作为一类典型的多部件系统,串并联系统体现了复杂系统的基本特性,是非常好的研究对象。串并联系统中部件的经济相关性体现在:当决定同时维修两个及以上部件时,维修费用和时间会有一定程度的节省;若对两个及以上相同的部件采取相同的维修方式,也能导致费用和耗时上的缩减。由于部件共同维修时可以分摊准备费用,当共同维修的部件数量增加时,相应的维修费用和耗时也会减少得更多。这也意味着当系统因部件故障而停机时,若对非故障部件进行预防性维护,可以节省停机成本。但已有文献中考虑部件经济相关性的选择性维护模型多以计划停机为背景,较少考虑以系统故障停机为背景的非计划停机场景下的选择性维护研究。
因此,将选择性维护引入多状态串并联系统的非计划停机维修决策中,研究系统因多故障并发而停机的情形下,如何在有限的资源限制下安排系统各部件的检修活动,使得系统能尽量长时期维持在一个较好的运行状态。
1 问题描述
研究的串并联系统由M个相互独立的子系统串联而成,如图1所示, 其中,第i(i=1,2,...,M)个子系统由Ni个相同的部件并联而成。
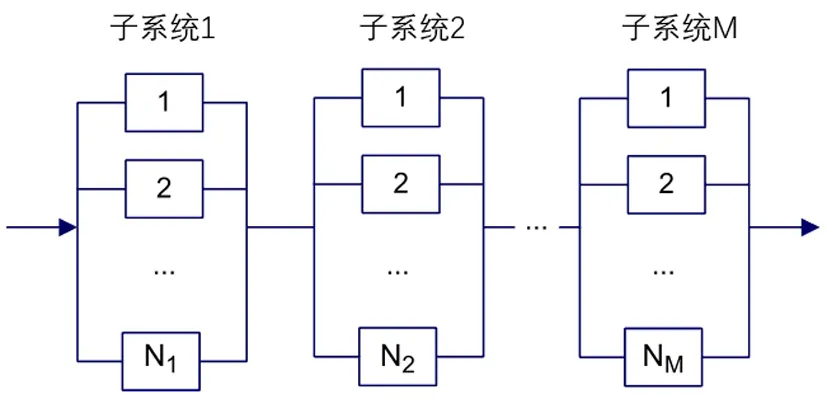
图1 串并联系统示意图
用S描述部件或系统所处的状态可能集合,K表示最佳状态值,0表示故障状态值,则每个部件和系统的所有可能状态有K+1种,即S={0,1,...,K}。系统从某个已知状态开始运行,运行时间达到t后,用sij(t)表示BJ(i,j)(第i个子系统中第j个部件)此时所处的状态,则BJ(i,j)在运行时间达到t后处于状态k的概率pi,j,k(t)定义为(1)所示,
pi,j,k(t)=P{sij(t)=k}
(1)
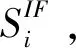
Y={Yij},(i=1,2,...,M,j=1,2,..,Ni)
(2)
X={Xij},(i=1,2,...,M,j=1,2,..,Ni)
(3)
研究问题有如下假设:
(1)系统由M个子系统串联而成,每个子系统由任意个相同的部件并联而成;
(2)每个部件的工作状态均有K+1个,即除完全失效和正常运行外,部件工作状态值还可以介于两者之间,且部件状态在系统运行过程中存在劣化过程,即逐渐从最佳状态退化至完全失效状态;

(4)系统状态需要在有限的时间和费用约束内得到恢复;
(5)系统及组成单元在失效过程中表现出多状态的特征,同一个子系统中的设备完全相同,各设备状态的劣化转移强度(Transition Intensity)是已知的,系统的可靠度能够被准确估计;
(6)维修活动不可能造成设备状态的退化,即Yij≤Xij;
(7)系统恢复运行后,要求在时间τ内满足最低状态值要求D的条件下正常运行;
(8)任何针对单个部件BJ(i,j)将其从Yij恢复至Xij的单独的维修活动所需的费用和时间为已知的常量;
(9)系统修复后至任务结束期间无意外故障发生。
2 模型建立
建立的模型用于在有限的维修时间T0和费用C0约束下,决策故障部件的维修方式以及选择进行机会维护的部件和维护程度,以保证系统在接下来的时间τ内达到最低状态值D的基础上,提升系统的整体可靠性。
2.1 系统可靠性
假设BJ(i,j)从最佳状态K开始运行,在每个状态的停留时间满足指数分布,其性能逐级退化过程如图2所示,由于同一个子系统中部件相同,则子系统i中任一部件BJ(i,j)从状态k到状态k-1的劣化转移强度可用λi,k表示[19]。因此若BJ(i,j)从起始时刻0开始以状态K开始运行,考虑部件的性能退化过程,BJ(i,j)在t时刻处于各状态的概率集合如(4)所示,在t时刻其状态概率可以通过求解如(5)所示的Chapman-Kolmogorov(C-K)等式得到[20]。

图2 部件的性能退化过程示意
Pij(t)={pi,j,0(t)·pi,j,1(t)·…·pi,j,K(t)}
(4)
(5)
若系统运行时间段τ后,φ(τ)表示系统整体所处的状态值,φi(τ)表示子系统i所处的状态值,系统的可靠度指系统在正常运行时间段τ后所处状态仍满足状态值大于等于D的要求的概率,即Rs(τ,D)=P(φ(τ)≥D)。系统可靠度可由式(6)计算得到
(6)
2.2 多态部件的维修选择
通常来说,对于一个多态部件有多种维修或维护方案可供选择,所有的方案大致可分为如下三类
(1)保养:不改变部件的状态,即Xij=Yij;
(2)替换:部件修复如新,即Xij=K;
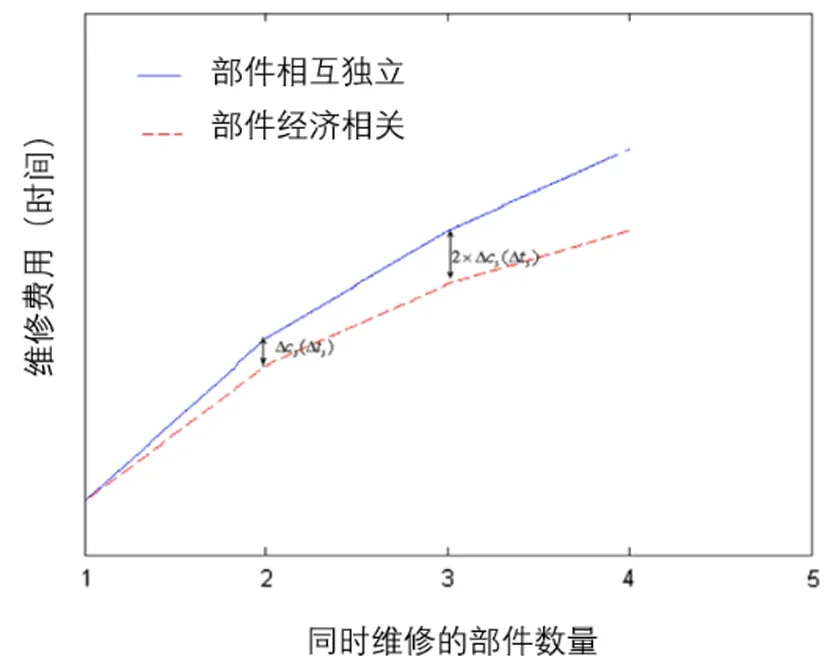
(3)非完美维护:部件状态提升,但达不到最佳状态,即Yij 由于同一个子系统中部件相同,则子系统i中任意部件BJ(i,j),若在维修期间将其状态从Yij提升至Xij,则其费用支出均为ci(Yij,Xij)个单位成本的。若BJ(i,j)在维修期间只是稍作保养,即状态值维持原状,有Xij=Yij,ci(Yij,Xij)=0。若Yij i=1,2,...,M (7) 则维修期间系统的维修费用为所有部件的维修费用之和,如式(8)所示, (8) 同理,由于同一个子系统中部件相同,可将ti(Yij,Xij)0.5定义为系统i中任意部件BJ(i,j)在维修期间将其状态从Yij提升至Xij的单位耗时,子系统i中BJ(i,j)所有可能的ti(Yij,Xij)组成的(K+1)(K+1)的耗时矩阵可用同一个耗时矩阵表示,如式(9)所示。 i=1,2,...,M (9) 假设系统中部件的维修依次进行,则维修期间系统的维修时间之和为所有部件的维修时间之和,如式(10)所示 (10) 图3 考虑“固定成本”节约的维修费用(时间) 随共同维护部件数量的变化 图4 维修相同部件的成本变化 因此,系统总的维修费用如式(11)所示。 (11) 式中: 类似地,系统总维修时间如(12)所示 (12) 式中: 定义的维护问题可由非线性整数规划模型描述如下 maxRS(X,τ,D) s.t.CM(X)≤C0 TM(X)≤T0 Yij (13) 考虑如图5所示的串并联系统,其中M=3,N1=3 ,N2=2,N3=4,S={0,1,2,3},不同于文献[16],对系统选择性维修决策设置了多故障并发这一情境,该情境下系统失效时的状态量为Y=[1 0 1 0 0 0 1 1 1],即部件BJ(1,2),BJ(2,1),BJ(2,2),BJ(3,1)故障,假设任一子系统中的部件为相同部件,三个子系统中部件的状态劣化转移强度见表1。 图5 串并联系统算例 表1 算例中各子系统部件转移强度 子系统编号状态转移强度(单位:每年)k=3k=2k=110.060.110.0520.140.090.230.110.080.16 对于任一子系统i中的BJ(i,j),i=1,2,3,ti(a,b),ci(a,b)已知,则由式(8)、( 10)得到各子系统部件相应的维修费用和维修时间矩阵如下所示, 将不考虑部件经济相关性情境下的最优方案命名为strategy1,考虑部件经济相关性情境下的最优方案命名为strategy2。两种方案均通过遗传算法[21]求出,算法的参数设置如表2所示。 表2 遗传算法参数设置 两种方案的最优解如表3所示,当维修决策考虑部件经济相关性时,联合维护活动会增多。strategy1中维修活动耗时17个单位时间,耗费31个单位费用,strategy2中维修活动耗时11.1个单位时间,耗费24.5个单位费用。不考虑经济相关性的方案所需耗费的时间和费用均高于考虑经济相关性的方案,但前者的可靠度低于后者。 表3 最优维修方案 图6 系统可靠性 VS 费用约束 接下来探讨上述两种情形下,随着资源预算的增减,系统可靠性的变动情况。如图6,图7所示,考虑部件经济相关性的维修方案对时间和费用的约束更敏感,但两种情形下系统可靠性随着资源预算的变动趋势较一致。 考虑部件经济相关性时,分别观察最佳维修方案在与部件经济相关性密切相关的参数变动时对维修时间和费用的影响,如图8所示,维修耗时和费用变动趋势相似,联合维修活动带来的费用节省越多,整体维修活动的资源消耗越少。对相同部件采取完全一致的维修活动,单个部件的费用增加时,整体维修活动的资源消耗也会增加。由于子系统1中三个部件的初始状态完全不同,因此子系统1的费用节省因子对整体费用没有影响,而子系统2中所有部件的初始状态均相同,因此子系统2的费用节省因子对整体费用的影响最大。对维修耗时的分析与此类似。 图7 系统可靠性VS 时间约束 图8 经济相关性参数设置对维修时间和费用影响分析 为探究部件的维护成本对上述两种情形下资源消耗的影响,接下来分析各子系统部件相应的维修费用和维修时间矩阵成倍缩放时,维修方案消耗资源的变化情况。如图9所示,无论是否考虑部件的经济相关性,整体维修活动的耗费随维修费用矩阵的变化趋势相差不大。相比于与部件经济相关性有关的参数变动,维修费用矩阵和时间矩阵对维修活动费用和时间消耗的影响比重更大。 图9 部件维修成本对维修时间和费用影响分析 在建立了有限的时间和费用约束下以最大化设备可靠性为目标的维修方案选择优化模型基础上,对比分析了时间费用约束下,考虑部件经济相关性与不考虑部件经济相关性的维修方案的异同。并将遗传算法用于基于维修目标、时间和费用约束的模型求解中,通过算例说明了该模型纳入经济相关性的因素后对维修决策的制定有较大影响。 基于多状态系统的特征,假定设备在各状态之间的转移概率已知或状态劣化率已知,并由此计算设备的失效率或系统可靠性,但在现实生产中,设备失效率或系统可靠性无法如假设的如此易得,如何使模型的必要元素——设备失效率或系统可靠性与现实情况更加贴合,有赖于对系统尤其是复杂设备的故障规律进一步探讨和研究。 研究了时间和费用约束下事后维修效率的优化,但实际生产中,制约维修方案设计的约束包括但不仅限于时间和费用,接下来的研究可以将人员、备件等其他有效约束纳入维修决策建模寻优中。2.3 考虑部件经济相关性的维修费用与耗时
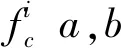
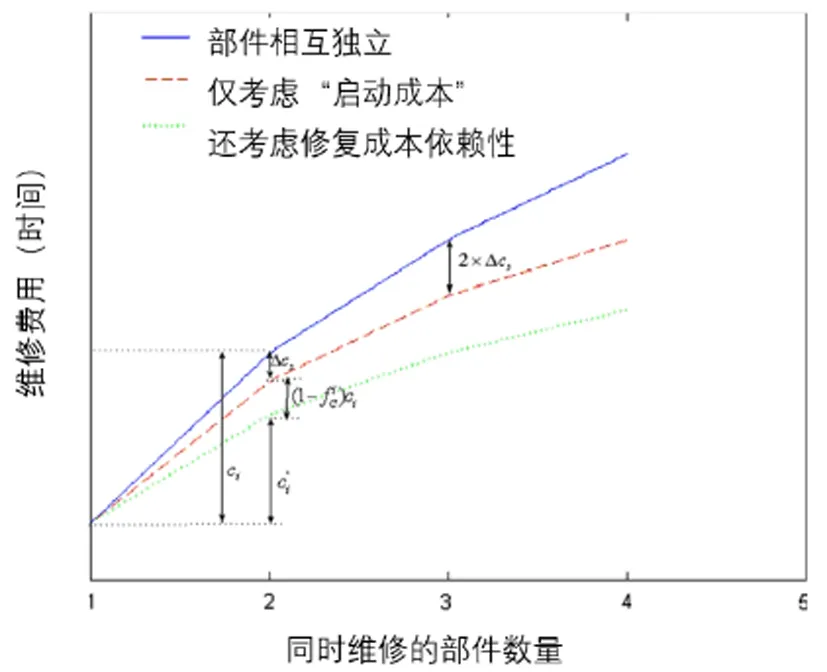
2.4 模型的优化目标与决策变量
3 算例分析
3.1 算例建模与求解
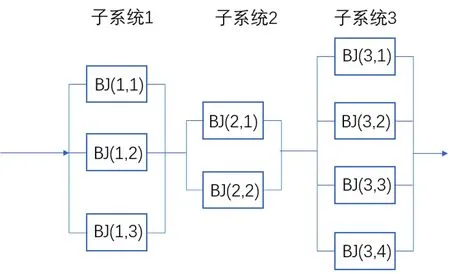
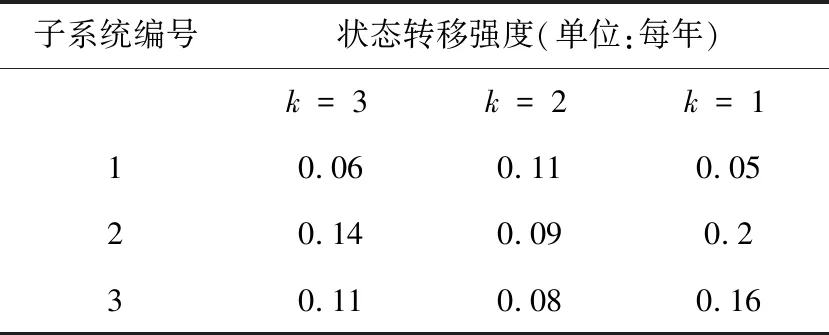
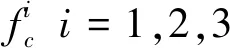
3.2 结果分析



4 结 语

