熵权决策模型在施工项目评标中的应用研究

苏海花

（江苏开放大学建筑工程学院，江苏 南京，210017）

招投标活动作为建筑工程的重要环节，受重视的程度越来越高。从建设项目立项到竣工验收，在多个环节涉及到招投标活动，主要包括设计单位、监理单位、施工单位等的确定。而作为招标文件的一个重要组成部分，即评标方法与评标标准的确定对选取合适的施工企业至关重要，而且评标办法如同一个指挥棒无疑对投标人的技术方案、特别是其报价行为有着最直接的影响[1]。所以，在编制招标文件时一定要从客观的角度出发，选择具有针对性强、可操作、又切合招标工程实际的评标方法和评标标准，进行工程评标是科学发展的必然趋势。

根据现行《标准施工招标文件》规定的评标方法主要有经评审的最低投标价法和综合评估法。最低价投标价法以价格作为唯一评标标准；在综合评估法中，一般做法是由评标专家根据招标文件中规定的评标标准对每份投标文件中相应的指标进行打分，然后对评标专家的打分进行平均或者加权平均处理，进而计算出每个投标人的得分，最终确定中标者。这种评标方法主观性较强，而且还可能存在人为干扰，对评标结果的客观合理性造成一定影响。

鉴于以上原因，相关学者对工程评标方法进行了深入研究，形成了相应的评标体系。例如，神经网络模型、主成分分析法、模糊综合评价法，还有将德尔菲法和层次分析法相结合应用于招投标中，利用德尔菲法制定评价指标等。在以上研究的基础上，利用熵权决策法将项目客观情况与主观判断相结合确定评价指标及其权重，尽可能使评标结果更加符合客观实际，从而提高评标方法的科学性，而且借助EXCEL 软件可在短时间内完成整个计算过程。

1 熵权决策法概述

熵权决策法是根据被评价对象的指标值构成的判断矩阵来确定指标权重的方法[2-7]。若有n 个评价对象，每个评价对象有m 个评价指标，在n 和m 都确定的情况下，熵权并不表示某个指标的重要性，而是各个对象在各个指标上竞争的相对激烈程度。

熵权有如下性质[8]：

（1）各个被评价对象在某个指标上的值完全相同时，熵值达到最大值1，熵权为0。这意味着该指标未向决策者提供任何有用的信息，该指标可以取消；

（2）各个被评价对象在某个指标上的值差异较大，熵值较小，熵权较大。这意味着该指标向决策者提供了有用的信息。同时，还说明各个被评价对象在该指标上有明显差异，应重点关注；

（3）各个被评价对象在某个指标上的熵值越大，其熵权越小，该指标越不重要；

（4）各个被评价对象在某个指标上的熵权大小，从信息角度来看，反映了该指标提供有用信息的量的多寡程度；

（5）各个被评价对象在某个指标上的熵权大小与被评价对象有直接关系。

2 基于熵权的建筑工程施工项目评标模型

2.1 评价指标体系构建

评价指标体系设置得科学、适度与否，关系到评标结果能否客观地反映投标单位的实际情况、能否公正地选出合适的施工单位。评价指标体系的构建应遵循科学性和实用性、可操作性和发展性、系统性和层次性、针对性和独立性、定性与定量相结合的原则[9]，通过调查分析、资料整理，结合工程实际情况等因素，从商务报价、基本经营状况、项目管理能力、施工能力、资源能力等几大方面构建指标体系，共包含17 个二级指标[10-11]，如图1 所示。

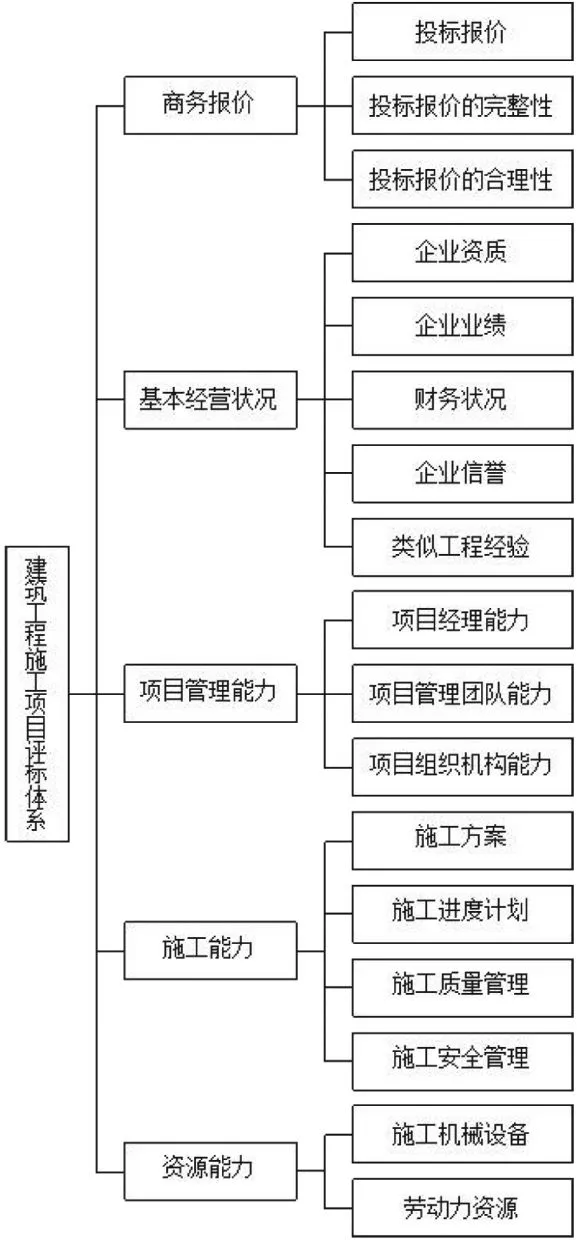
图1 建筑工程施工项目评价指标体系

2.2 基于熵权的评价指标权重计算[12]

2.2.1 构造评价指标判断矩阵

建筑工程施工项目招标，采用综合评估法，共有m 个评价指标，n 个施工单位参与投标，则n 个投标方案的m 个指标值构成判断矩阵B’：

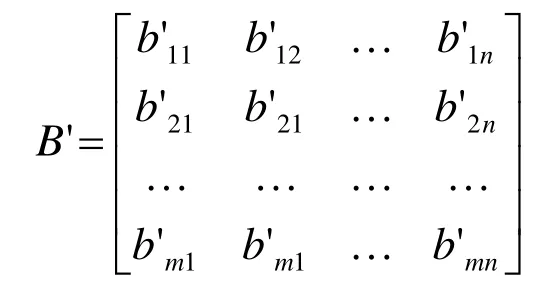
其中元素b'ij为第j 个投标方案在第i 个评价指标上的值，该值由评标专家打分确定。

2.2.2 评价指标标准化处理

为消除量纲等因素的影响，利用公式（1）将判断矩阵作标准化处理，

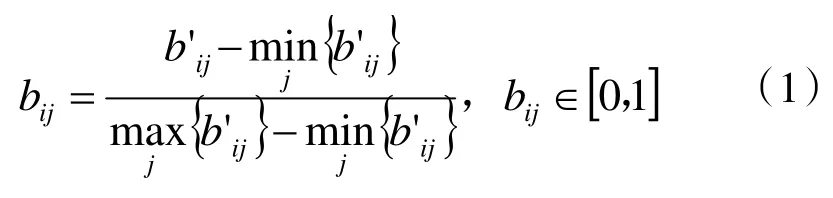
式中，b'ij——第j 个投标方案在第i 个评价指标上的值，i=1,2,…,m；j=1,2,…,n

bij——评价指标b'ij经过标准化处理的值

在建筑工程施工项目评标时，所有的评价指标均为越大越优，即均为收益性指标。

得到标准化判断矩阵：

其中，bmn为第n 个投标方案在第m 个评价指标上的值b’mn经过标准化处理的值。

2.2.3 确定评价指标的熵值

式中，Hi——评价指标b'ij的熵值，i=1,2,…,m；j=1,2,…,n

Pij——确定评价指标熵值Hi的中间量

同时，在建筑工程施工项目招投标时，通常不会出现Pij=1 的情况，所以此处不予讨论。

2.2.4 确定评价指标的熵权

第i 个评价指标的熵权Wi1为

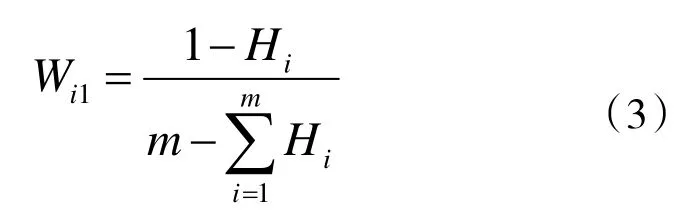
式中，Wi1——评价指标b'ij的熵权，i=1,2,…,m；j=1,2,…,nm——评价指标的数量

Wi1满足0≤Wi1≤1 和

2.3 构造综合权重，确定最优方案

2.3.1 构造评价指标的综合权重

基于熵权确定的评价指标的权重较为客观，但可能也会出现不能反映工程实际情况[13]，使设置的权重与该指标的实际重要程度不符。只注重对数据客观信息进行分析，过分依赖客观数据，会使结果中客观因素所占比例过大；而只注重通过专家评分来对权重结果进行数学分析，又会使结果中主观因素干扰过大。此时，可以结合建设单位的主观意愿，由专家根据其实际经验对各项指标设置权重Wi2。综合二者，得到一个综合考虑主客观因素的评价指标权重Wi：

式中，Wi——评价指标b'ij的综合权重，i=1,2,…,m；j=1,2,…,n

Wi2——根据专家经验设置的评价指标b'ij的权重，i=1,2,…,m；j=1,2,…,n 2.3.2 确定最优方案

将综合权重Wi构成的矩阵和指标判断矩阵B'相乘，得到综合评分水平矩阵A，对此综合评分水平矩阵A 中的元素Aj进行排序，求得最大值A0，A0对应的方案即为所要确定的最优方案中，即：

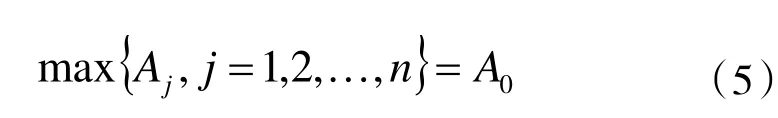
式中，Aj——第j 个投标方案的综合评分，j=1,2,…,n

A0——n 个投标方案中，综合评分最大值

即为所确定的最优方案。

3 实例应用

3.1 评标方法及评价指标值

某学校教学综合楼项目施工总承包进行招标，工期725 天，招标范围为教学综合楼施工总承包，包括土石方、桩基、基坑支护、土建及水电安装、幕墙、钢结构、消防、室内装修、智能化、通风空调、景观工程、室外道路、管网等。

投标文件包括技术标和商务标两部分。开标、评标活动分两个阶段进行：第一阶段：技术标开标、评标。评标委员会先评审技术标（包括投标项目负责人答辩），技术标评审采取评分制，只有技术标评审得分排前几名的投标人（具体数量在招标文件中明确，投标人为12 个及以上的，取前9名；投标人为9-11 个的，取前7 名；投标人为8 个及以下的，取前5 名）才能进入第二阶段开标、评标。第二阶段：商务标开标、评标（仅针对进入第二阶段的投标文件进行），并将第一阶段技术标评分带入第二阶段。

经资格审查，本次招标共有6 家投标企业符合要求，先进行第一阶段评标，根据投标人提交的技术标，结合招标文件的评标要求和图1 的评价指标体系，由评标专家对各个技术标对应的各评价指标进行打分，评分结果见表1，用熵权模型对这6 个投标方案进行比较，确定5 家企业进入第二阶段评标。

表1 投标单位在评价指标上的得分

3.2 评价指标值标准化处理

将表1 指标值按照公式（1）作标准化处理，得到标准化判断矩阵B：

3.3 计算评价指标的熵值

按照公式（2）计算各评价指标的熵值Hi，得到熵值矩阵H：

3.4 计算评价指标的熵权

按照公式（3）计算各评价指标的熵权Wi1，得到熵权矩阵Wi：

3.5 计算评价指标的综合权重

本项目中专家评价各指标权重，如矩阵W2：

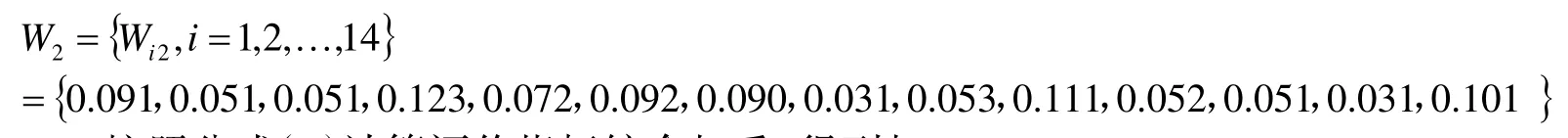
按照公式（4）计算评价指标综合权重，得到权重矩阵W：

3.6 方案排序，确定第一阶段评标结果

将权重矩阵W 和表1 得分数据相乘，得到综合评分水平矩阵A：

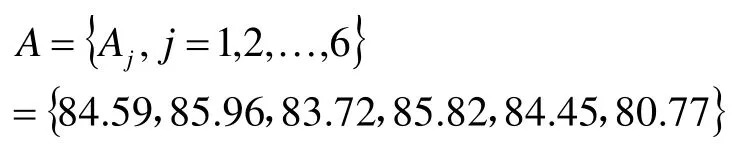
根据得分高低，将第一阶段评标结果进行排序：企业2＞企业4＞企业1＞企业5＞企业3＞企业6。由此，可以确定企业6 不能进入第二阶段评标，企业2 的得分最高，企业4 次之。

3.7 通常评标计算方法

在传统的综合评分计算中，一般只考虑专家权重，即将专家权重矩阵W2和表1 数据相乘，得到综合评分水平矩阵A'：

按综合评份高低排序，为：企业4＞企业2＞企业5＞企业1＞企业3＞企业6，同样也是企业6不能进入第二阶段评标，但是企业4 得分最高，企业2 得分次之。

4 结论

通过比较熵权评标和传统评标的结果，可以看出，在第一阶段评标时，有6 家企业参与投标，剔除的单位是相同的，好像没什么区别。但是根据评标办法，第一阶段得分带入第二阶段，从以上得分情况和排序高低可以看出区别较大。究其原因是专家在确定权重时会受到主观因素影响，会将其认为比较重要的指标设定的分值偏高；而认为不是那么重要的指标，设定的分值相对较低。而应用基于熵权评价模型确定评价指标的权重，比较客观。并将主、客观权重相结合，既考虑专家经验，又能客观公正地确定评标结果。因此，具有较好的实用性。