基于改进灰色预测模糊PID控制的列车多目标优化研究
孟建军,张宏强
(1.兰州交通大学机电技术研究所,兰州 730070; 2.甘肃省物流及运输装备信息化工程 技术研究中心,兰州 730070; 3.甘肃省物流及运输装备行业技术中心,兰州 730070)
随着城市人口的急剧增加,城市化进程的不断推进,城市交通问题变得尤为突出,这严重限制了城市经济发展速度。城轨列车具有缓解交通拥挤、节约能源、安全等优势,并能确保在多目标前提下正常运行。因此,运用城轨列车解决与处理日趋严重的城市交通问题已成为不可或缺的重要方式。目前,城市轨道交通绝大部分都采用ATO控制,而一小部分仍采用传统的人工驾驶方法,这种传统的控制方法致使因司机手动操纵不当造成舒适度差和停车精度低等问题。可见,人工驾驶已无法满足对列车高效运行的控制需求,采用ATO控制方式可最大程度满足列车运行各项性能要求。
列车ATO系统是列车运行速度控制的关键,而搭建与设计有效可行的控制算法是ATO系统操纵的核心。因此,有效可行的控制算法能使列车时刻处于最佳行驶状态,并改善和提高运行效率、停车精度与降低能耗[1]。对列车ATO系统控制算法而言,先依据已知信息优化控制策略,然后采用控制器控制车辆牵引与制动系统,控制列车跟踪生成的目标曲线[2-3]。跟踪曲线的精准程度取决于采用的控制算法,通过跟踪曲线和目标曲线的贴近度评判算法的优劣[4-5]。ATO系统控制算法的研究是从PID控制算法发展到参数自适应控制算法,再到智能控制算法与集成智能控制算法[6]。目前使用的ATO系统控制算法主要以PID算法为主,其控制参数一旦确定,则在控制与优化过程中是固定不变的[7-8]。改进的PID控制算法以PID算法为基础,对控制参数实时调整,克服PID控制不能适应整个行驶过程的缺陷[9]。模糊控制是通过操纵经验确定控制策略,铁科院提出一种基于模糊控制ATO控制算法——直接模糊神经控制[10]。但模糊控制具有滞后的缺点,需引进预测控制来解决其滞后性问题[11]。日本学者Hiroyasu Oshima将模糊控制和预测理论相结合应用于车辆控制,通过提取司机的操控经验,设立准时、安全、舒适和节能等指标,搭建了预测模糊控制器[12]。唐涛等在确保车辆停车时间误差在规定范围的前提下,为了降低能耗,采用了延长其惰行距离的途径[13]。施鸿宝等针对车辆自动运行控制过程,采用模糊控制和BP神经网络控制进行定位停车,但在精准停车时并没有考虑行驶中未知非线性扰动因素[14]。何之煜等在考虑扰动的情况下,将自适应模糊滑模控制引入精确停车过程中,从而增强了ATO系统的鲁棒性,达到了较高的停车精度[15]。孟建军等引入物元理论建立速度轨迹模型,并采用优度评价法选取决策速度,实现了多目标最优[16]。
从上述研究可知,众多学者研究列车ATO系统的算法较广泛,为了更好地满足列车运行各项性能要求,需探究更有效的控制算法。灰色预测控制不仅能改进ATO系统的滞后性,同时也能提高其预测控制精度,在预测控制中产生更多的信息与数据[17-18]。列车运行过程是时变不确定的,根据灰色预测控制中灰色作用量具有动态特性,提出对灰色预测控制进行改进。将灰色预测控制、模糊控制、PID控制优势互补,结合成改进灰色预测模糊PID控制算法,得到列车全程运行的最佳多目标控制,实现了整个运行过程的最优。
1 ATO多目标模型的构建
1.1 列车动力学模型
根据列车当前运行速度、停车距离、时间,建立符合列车运行的运动方程[19]

(1)
式中,v为列车运行速度,km/h;t为时间,s;x为距离,m;g为重力加速度,m/s2;γ为回转质量系数,一般取0.06;Je为列车能耗,kW/h;φ(t)为列车单位时间内能量消耗函数,kW;T为列车全程运行时间;c为列车单位合力,N/kN。
式(1)以t为独立变量。为了更适合改进灰色预测模糊PID控制,在实际运算中用距离x为变量,故将列车运动方程修正为以距离x为独立变量的函数。

(2)
列车所受合力主要为列车输出力、附加阻力和基本阻力,构建其合力方程
c=f(v)-w0(v)-b(x)
(3)
式中,f(v)为列车单位牵引或制动力;b(x)为列车附加坡道阻力,由坡道、隧道及曲线等折算坡度组成;w0(v)为单位基本运行阻力,其值由式(4)决定
w0(v)=A+Bv+Cv2
(4)
式中,A为运行阻力系数;B为滚动阻力系数;C为空气阻力系数。
简化式(2)~式(4),得列车动力学方程

(5)
列车坡道附加阻力计算为

(6)
式中,N是车厢数;bi(x)是每节车厢附加阻力。
综上,得列车动力学方程表达式

(7)
满足t(0)=0,t(X)=T,v(0)=v(X)=0,v(x) 其中,x∈[0,X]为独立变量;v∈[0,V]和t∈[0,T]为状态变量,V为列车最高允许速度,(t,v)∈[0,T]×[0,V]⊆R2。 1.2.1 准时性模型 (8) 式中,σ为允许的早晚点时限,一般情况下车辆运行时间不超过规定时间的5%都可满足准时性要求;σ0为惩罚项系数,表示晚点时间在σ范围内时,车辆准时所需的能耗;Kt反映车辆准时性指标,当车辆运行早晚点时间超过σ时,Kt值迅速增大;当早晚点时间恰好在内σ时,Kt值较小;因此,Kt值可反映车辆运行正点情况,可作为列车运行准时性性能指标。 1.2.2 舒适性模型 舒适性反映了乘客满意程度,通常用车辆运行的纵向加速度及其变化率表示。故舒适性模型为 (9) 式中,Kc为评价列车舒适性性能指标。Kc越小,表明其舒适性越好,且列车在牵引或制动过程中纵向冲击率不应大于0.75 m/s3;ai和ai-1分别表示第i个和第i-1个软件处理周期时的加速度。 1.2.3 精准停车模型 列车实际停车地点表示为 (10) 式中,Kd表明列车到目标停车点的距离与实际行驶距离间差值越小,其停车后位置越接近实际停靠点。因此Kd可作为列车停车精准性性能指标。 1.2.4 能耗模型 当所需的(t,v)∈[0,T]×[0,V],列车在[0,T]内产生的能耗 (11) 因主要考虑列车的运行过程,故其能耗模型可改写简化为 (12) 式(12)中:Ke为能耗指标;ai-1为第i-1个工况时的加速度;xi和xi-1分别表示在第i个和第i-1个工况转换点时的位置。 综上所述,以准时性、舒适性、精准停车及能耗为目标,搭建多目标优化模型 (13) 为了合理有效地求解与处理多目标优化问题,应用加权求和的方法将其巧妙地转换成单目标优化问题。因此,可得到总体评价指标函数为 f=ω1Kt+ω2Kc+ω3Kd+ω4Ke (14) 然而在本文中只有当适应度取值充分大时,才能满足各个评价指标总体最优,故适应度函数为 F=1/f (15) 式(14)中,ω1、ω2、ω3和ω4分别表示各性能指标对应的权重系数,满足ω1+ω2+ω3+ω4=1。为了获得列车最佳控制策略,依据文献[21]中考虑自身数量级和对其控制效果的影响程度进行调整权重,因此,本文取ω1=0.3,ω2=0.2,ω3=0.4,ω4=0.1。 ATO系统控制策略不仅要满足其运行速度不能超过限制速度,更要符合运行工况转换原则。当车辆在行驶条件相同时,其运行能耗取决于工况的选择。为了探究ATO控制策略,需分析其工况转换原则。工况转换原则见表1。 表1 工况转换原则 注:⊙表示不需转换;○表示允许转换;●表示禁止转换 由表1可见,该原则要求最终工况必须是制动工况,起始工况必须是牵引工况。牵引与制动工况间无法直接完成转换,需中间经过惰行工况。同时要避免各种工况间频繁转换。当列车进入某一工况时,为了减小能耗,应在该工况下保持其行驶一段时间。为了模拟理想中ATO控制行车的场景,经过以上分析,将选取牵引—惰行—牵引—惰行—制动—惰行—制动的控制策略。 列车ATO运行过程很难建立与设计精确列车运动模型。因此将列车视为一个质点,且忽略列车间的相互作用,采用文献[20]中列车模型作为传递函数。列车模型表达式为 (16) 式中,G表示传递函数;s表示复变量。 PID控制器控制规律可由式(17)或式(18)描述 (17) (18) 其中,KP、KI、KD分别为比例、积分、微分系数,e(t)为控制误差。PID控制作用u(t)由控制误差e(t)的KP、KI与KD通过线性组合表示。本文通过多次试凑,最后选取KP=15.5,KI=13.4,KD=13.1。用Simulink 2016a模块所设计与搭建的基于PID控制器列车自动驾驶运行仿真模型如图1所示。 图1 PID控制器仿真模型 由于PID中的KP、KI、KD的大小直接由构建与设计的控制对象高精度数学模型所决定。然而,列车实际运行过程复杂多变,运用PID控制无法取得理想的控制效果。为了攻克PID不能适应列车整个运行过程控制的缺点,巧妙地将稳态控制好的PID控制和动态响应快的模糊控制相结合,建立模糊PID控制器[21]。 本文形成的模糊PID采用e、ec两输入与ΔKP、ΔKI和ΔKD三输出的控制结构。经模糊化、模糊推理与反模糊化,随时在线KP、KI与KD进行修正,以充分满足不同工况e、ec对PID参数的要求。定义e、ec在模糊集中论域的范围e,ec={-13,+13},模糊子集e,ec={NB,NM,NS,ZO,PS,PM,PB};ΔKP、ΔKI和ΔKD的模糊子集为{NB,NM,NS,O,PS,PM,PB},ΔKP的论域范围为{-0.05,+0.05},ΔKI、ΔKD的论域均为{-0.002,+0.002}。为了满足系统的稳定性与鲁棒性要求,其隶属函数均为三角形,且模糊推理选用Mamdani推理方法,反模糊化选用重心法。图2为运用Simulink 2016a模块所设计与搭建的基于模糊PID控制器列车自动驾驶运行仿真模型,其中图2中PID controller1为图1模型。 图2 模糊PID控制器仿真模型 灰色预测是运用灰色模型GM(M,N)进行的定量分析预测,即采用少量的、不完全的信息,构建数学模型并做出科学合理分析预测的一种方法。灰色预测是以灰色模型GM(M,N)为基础,定义该模型GM(M,N)中M为阶数,N为变量个数。常规的灰色模型主要为GM(1,1)模型,通常也选用GM(1,1)模型研究某些控制问题。在灰色预测时,常规的GM(1,1)模型视灰色作用量为一个常量,虽然简化了模型,但与车辆运行特征大相径庭。在GM(1,1)模型的基础上,将灰色作用量转换为动态形式,选取列车运行原始数据,发掘规律,获得预测值数列,对数列逆运算,获得预测结果。 针对列车ATO系统得到输入与输出时间序列: (1)输入序列 u(0)(1),u(0)(2),…,u(0)(n),n≥4 (19) (2)输出序列 x(0)(1),x(0)(2),…,x(0)(n),n≥4 (20) 式(19)、式(20)中,u(0)(k)和x(0)(k)分别为系统的输入与输出时间序列。由于式(19)、式(20)测得的数据是杂乱没有规律的,所以需对这些原始数据进行累加,获得有规律的数据序列 (21) (22) 建立优化GM(1,1)模型灰微分方程为 (23) x(0)(k)+az(1)(k)=b0+b1k (24) 式中,a为发展系数;b0+b1k为改进后的灰色作用量。 改进优化后的参数列为 (25) 令X=[x(0)(2),x(0)(3),…,x(0)(n)]T (26) 辨识a,b0,b1,并通过最小二乘法得 (27) 经计算得白化方程 (28) 白化方程的解 (29) 对式(29)离散化 (30) (31) 选择运用递推法,进一步求得R步的预测值,即为 (32) 应用其构建与设计的改进灰色预测控制算法操纵列车运行时,科学恰当地选用预测步数R与建模维数n是精准超前地预测其系统变化的关键所在。一般情况下,预测步数R的取值和该系统的惯性与滞后性有关,惯性或滞后性越大,R则越大。经上述分析,同时依据文献[18],本文拟取n=5,R=3。 本文组合了改进灰色预测、模糊控制和PID控制,形成了改进灰色预测模糊PID控制算法,其控制器工作原理如图3所示。 图3 改进灰色预测模糊PID控制器工作原理结构 图4 改进灰色预测模糊PID控制器仿真模型 为验证所设计算法的有效性,选用城轨列车A型车,同时选取某地铁线路长1 953 m的站作为仿真区间,采用Matlab 2016a软件进行仿真。 列车牵引力公式 (33) 基本阻力公式为 w0(v)=2.755 1+0.014v+0.000 75v2 (34) 制动力公式为 (35) 式中,v0、vt分别为该区间内车辆运行初、末速度。 列车参数与线路参数见表2、表3。 表2 列车基本参数 表3 线路基本属性 根据列车参数及线路情况生成目标曲线,并用遗传算法优化,得到理想目标曲线。遗传算法是经过编码、生成初始种群、计算适应度、复制、交叉与变异等步骤来完成的[22-23]。在适应度函数建立后,设计种群数、种群迭代次数、交叉与变异概率的值,经分析确定对应的参数分别取50,300,0.8与0.05。采用以上分析的控制策略运行,得各控制序列运行距离(m)为:104.178-597.272-83.340-937.575-66.672-100.001-64.232。利用Matlab 2016a软件仿真,得到图5所示列车运行目标曲线。 利用Simulink 2016a模块,设计与搭建改进灰色预测模糊PID控制器,跟踪目标曲线,获得其跟踪曲线,并与PID、模糊PID控制器分别跟随获得的跟踪曲线作比较。仿真生成的v-t、a-t、s-t目标曲线与跟踪曲线对比如图6(a)、6(b)、6(c)所示。 图6 列车运行目标曲线和跟踪曲线 通过分析图6可知:跟踪目标曲线的过程中,相比采用PID控制与模糊PID控制获得的跟踪曲线,采用改进灰色预测模糊PID控制算法获得的跟踪曲线在工况转换时比较平缓光滑,没有呈现明显的振荡,几乎与目标曲线贴合。这表明该算法能实现对列车较好的操纵,使速度和加速度跟随效果较好,以确保其准时性、舒适度、精准停车性和能耗性性能指标。为了验证所设计的算法可行性与有效性,进行详细对比分析了列车运行各项性能指标。 (1)准时性。列车在该区间内规定运行时间为137 s。由图6(a)可见,改进灰色预测模糊PID控制算法控制下列车运行时间为137.4 s,PID控制算法与模糊PID控制算法控制下列车运行时间分别为138.6 s和138.2 s,可知,这3种算法虽都符合准时性要求,但经计算改进灰色预测模糊PID控制算法比PID、模糊PID算法的准时性分别提高了75%,66.7%。 (2)舒适性。舒适性是乘客乘车首要考虑的因素,当加速度波动明显时,乘客会感到不舒服,加速度及加速度变化率的大小直接关系到舒适性。由图6(b)可知,PID、模糊PID控制算法下列车运行加速度变化振荡较大,无法很好地跟随目标曲线,而改进灰色预测模糊PID控制算法下加速度变化不大,加速度值始终保持在(-1,1)区间内,满足舒适性要求。 (3)精准停车性。停车的精确性将直接影响乘客正常上下车,规定停车误差不超过±0.25 m均认为停车精度较高。将图6(c)局部放大得图7。 图7 s-t曲线局部放大 由图7可知,在改进灰色预测模糊PID控制算法下列车运行距离为1 953.05 m,列车到该指定站时,其精准停车误差为5 cm;PID、模糊PID控制下列车运行距离分别为1 952.78 m和1 952.86 m,其对应误差分别为22 cm和14 cm,虽然3种算法控制下停车误差均在误差范围内,但改进灰色预测模糊PID控制比PID、模糊PID算法控制下停车精度分别提高了77.3%,64.3%。 (4)能耗。牵引、惰行、制动等控制策略的选择直接影响能耗,列车在牵引与制动工况时都有能量耗散,在运行过程中,应尽量选用惰行工况来节省能耗。通过能量累计,经计算PID列车ATO控制的能耗约为3.235×105kJ,模糊PID列车ATO控制消耗的能耗约为3.031×105kJ,改进灰色预测模糊PID列车ATO控制消耗的能耗相对较小,约为2.946×105kJ。因此采用所提算法可有效降低能耗。 (1)针对单一算法难以满足列车运行各性能要求,分析了列车ATO工况转换原则,提取了灰色预测控制、模糊控制和PID控制的优点,设计了改进灰色预测模糊PID控制算法。该算法不仅具有改进灰色预测“超前控制”的优点,也具有模糊控制自适应强的特点,可实现PID参数在线调整。 (2)为对比其控制效果,本文设计搭建了PID控制器、模糊PID控制器和改进灰色预测模糊PID控制器,用于跟踪目标曲线。结果表明,相比前两种控制器获得的跟踪曲线,采用改进灰色预测模糊PID控制器得出的跟踪曲线几乎与目标曲线贴合。 (3)分析可知,改进灰色预测模糊PID控制算法比PID、模糊PID控制算法能提高与改善列车运行的准时性、舒适性、停车精准性以及降低能耗。 列车ATO控制是一个极其复杂、非线性的过程,在分析该问题时,简化了模型,将列车视为一个质点,搭建了单质点模型;同时本文仅采用改进算法仿真了一个区间运行,还有很多场景并没有考虑在内。因此,在后续研究中建立多质点模型,以更好地分析列车受力情况;同时,还需考虑运行过程中弯道产生的离心力、加速度以及列车在运行中重力变化等因素。1.2 列车ATO多目标模型
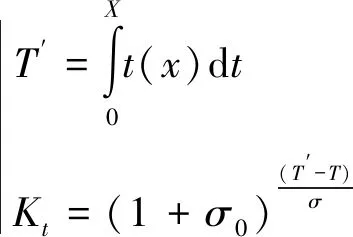
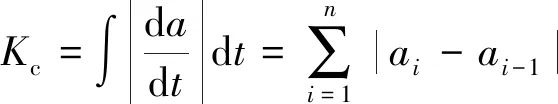

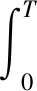
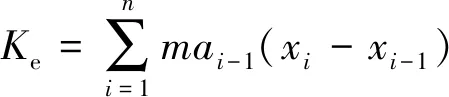
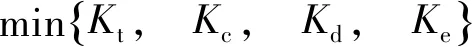
1.3 列车ATO系统控制策略分析

1.4 列车模型的建立

2 列车控制器设计
2.1 PID控制器原理及设计



2.2 模糊PID控制器原理及设计

2.3 改进灰色预测模糊PID控制器原理及设计

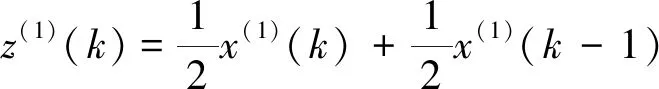

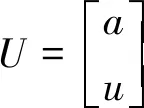


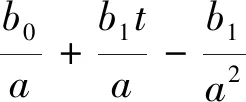






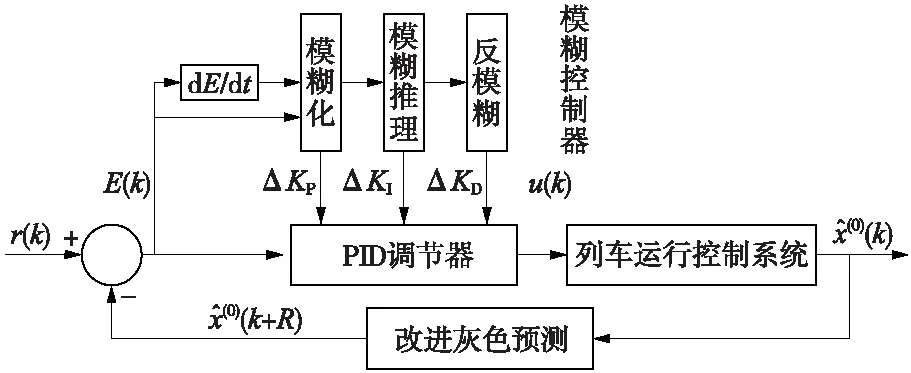

3 仿真分析
3.1 目标曲线的生成

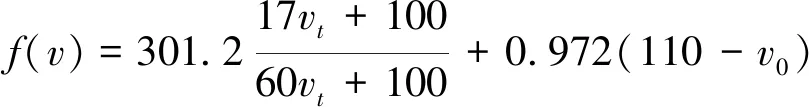


3.2 跟踪曲线的生成

3.3 仿真结果验证及分析

4 结论与展望

