基于关联分析和遗传算法优化BP的隧道围岩变形预测
王文玉,王希良,张 骞
(1.石家庄铁道大学交通运输学院,石家庄 050043; 2.石家庄铁道大学大型结构健康诊断与控制研究所,石家庄 050043)
引言
随着交通事业迅速发展,隧道工程被广泛应用在交通基础设施建设领域。隧道工程凭借缩短线路距离、避免高路堑等优势,建设比例不断增加。为确保运营和施工安全,其变形预测研究具有重要的意义[1-2]。
隧道施工时,由于各种地质灾害给隧道施工带来很大的难度。近些年来,很多国内外学者对于围岩质量、稳定性进行了研究和综合探索。吴波等[3]通过有限元数值计算对上软下硬地层隧道围岩稳定性量化评价标准进行了详细的分析和系统的研究,从而建立围岩稳定量化评价体系。刘明才[4]采用Monte Carlo方法,计算了岩体结构的可靠性,并分析了结构面参数的不确定性对块体稳定性的影响。涂瀚[5]对水平层状砂质板岩隧道的稳定性及破坏机理进行研究,为水平层状围岩隧道的建设提供参考。黄志平[6]通过RFPA方法考虑岩石材料的细观非均匀特性,对深埋硬岩隧洞全断面一次开挖和分断面多次开挖进行数值模拟分析,研究多个特征方面对围岩稳定性的影响及其破坏机制。张露晨等[7]利用关键块体理论矢量分析方法分析隧道围岩的稳定性。XIAO R Y, ZHU W, HE MC等[8-10]通过对滑坡进行监测,对滑坡下隧道围岩稳定性进行了一定的研究。
同时,围岩稳定性研究中,隧道围岩位移预测预报也是一项重要的内容,对施工决策有非常重要的意义。在现场测试中,多种因素的影响,监测数据存在偶然误差且具有离散性。在实际应用中,必须进行数学处理,找出量测位移在不同因素的影响下,随时间、空间变化的规律,同时预测其发展变化趋势,以科学地评价围岩的稳定性[11]。叶超[2]提出以粒子群算法对GM(1,1)模型参数进行优化,然后以BP神经网络为基础,建立误差修正模型,旨在进一步提高预测精度。张可能等[11]采用时空统一Kriging插值预测模型和DGM(1,1)灰色预测模型,预测隧道施工过程中掌子面前方一定范围内任意时刻的拱顶沉降。张碧[12]探讨不同小波变换参数的去噪效果,并将趋势项和误差项进行单项预测和组合预测,研究预测模型的有效性。文明等[13]通过引入动态施工影响因子作为附加的外部输入,结合模型本身的反馈结构和延迟单元,非线性动态地考虑隧道施工全过程。袁青等[14-17]对隧道预测问题做了一系列研究。总体来说,隧道围岩变形预测研究已取得了相应的研究成果,但仍存在一定的局限性,应提高对模型预测精度,更精确地应用于铁路隧道变形预测中[18]。
选取我国地势第二阶梯的川陕鄂黔中、低山区,以吴家沟隧道为依托。首先基于灰色关联分析,选取影响隧道围岩变形的主要因素。接着,基于生物进化的思想,用遗传算法优化BP神经网络,其分为三个部分。即BP神经网络结构确定、遗传算法优化和BP神经网络预测。遗传算法是一种全范围搜索算法,用遗传算法对BP神经网络参数进行优化,将遗传算法的全局搜索能力和BP神经网络的局部搜索能力相结合,避免BP神经网络参数选择上的随机性缺陷,预测结果更为精确。最后,应用工程实际,得到空间维预测结果,为工程实际应用提供借鉴。结果表明,在隧道围岩变形预测中,遗传算法优化神经网络精度高,满足隧道围岩变形预测精度的需要,对川陕鄂黔中、低山区隧道围岩变形预测有一定的参考意义。
1 关联分析
1.1 关联分析
关联分析是通过大量数据挖掘事物间的关联程度,基本原理是通过数据曲线几何形状的吻合程度判断联系程度。其过程如下。
STEP1:设系统特征序列为
x0={x0(k)|k=1,2,…,n}=
(x0(1),x0(2),…,x0(n))
式中,k表示时刻。并且存在l个相关因素序列,第i个相关因素序列为xi={xi(k)|k=1,2,…,n}=(xi(1),xi(2),…,xi(n)),i=1,2,…,l
STEP2:初始化系统特征及相关因素序列,得到初值像。
y0={y0(k)|k=1,2,…,n}=
(y0(1),y0(2),…,y0(n))
yi={yi(k)|k=1,2,…,n}=(yi(1),yi(2),…,yi(n)),
i=1,2,…,l
STEP3:求出y0和yi的关联系数。
ξi(k)=

(1)
为比较数列xi对参考数列在x0时刻的关联系数,分辨系数为ρ∈[0,1]。通常来说,ρ取0.5。
STEP4:式(1)定义的关联系数是描述比较数列与参考数列在某时刻关联程度的一种指标,定义

(2)
ri为数列xi对参考数列x0的关联度。
由式(2)可得,关联度是把过于分散的信息集中处理,即把各个时刻的关联系数集中为一个平均值。ri越大,表明xi对x0的作用越大。
1.2 影响因素
系统特征行为序列为隧道围岩变形值(x0),同时,围岩变形影响因素Xi(i=1,2,…,m)为相关因素序列,进行灰色关联分析。
除工程影响因素外,影响围岩稳定性及其变形的自然因素有很多,主要分为三大类,如表1所示[19]。

表1 自然因素
根据表1,选择以下指标:完整岩块强度特征指标包括饱和单轴抗压强度X1;岩体结构空间分布几何形态指标包括:岩石质量X2(用RQD衡量)、岩体体积节理数X3、可见迹长X4、间距X5。岩体结构面自身发育状况指标包括粗糙度X6、蚀变度X7、张开度X8、工程岩体质量([BQ])X9,同时该指标可以用总体指标来衡量,即岩体结构面自身发育特征(Jc)X10。地应力特征指标包括初始地应力X11。地下水状况指标包括地下水流量X12。工程因素指标包括开挖轴向与结构面产状组合关系系数X13,同时还包括隧道埋深X14。
利用式(1)及式(2)计算关联度时,需对X1,X2,…,X14数列做初始化处理。计算关联系数时,要求量纲要相同。现实问题中,不同数列具有不同的量纲,因此需对各种数据进行无量纲化。另外,为了易于比较,要求所有数列有公共的交点。为了解决上述两个问题,对给定数列进行变换。

这样,可对14个数列进行初始化处理。注意,对于随着里程增加,位移值也增加的数列,采用上述初始化变换;而对于与隧道里程成反比的数列来讲,进行初始化处理时,采取以下公式
将各个数列的初始化数列代入式(1)及式(2),算出各数列的关联度见表2(这里ρ=0.5)。
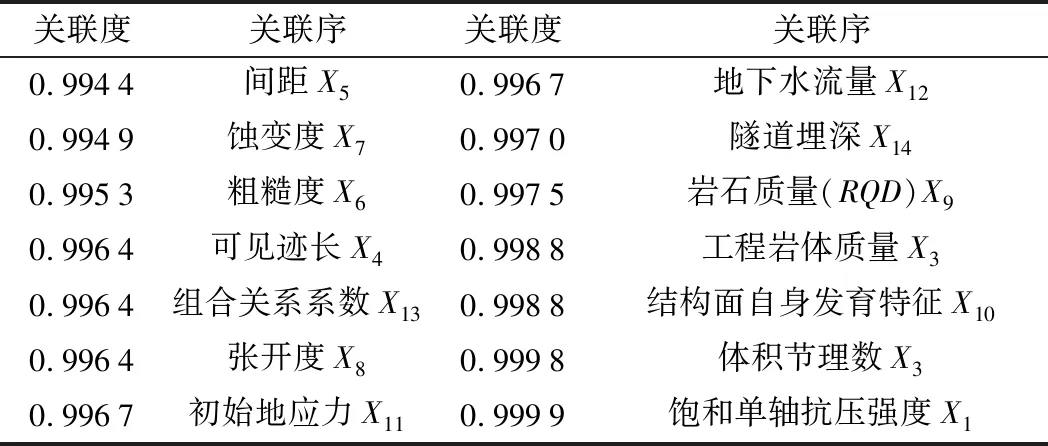
表2 关联分析结果
由表2可知,隧道埋深、岩石质量、工程岩体质量、结构面自身发育特征、体积节理数的关联度都在0.997以上,关联度非常高,因此选取以上因素作为影响隧道围岩变形的主要因素。同时考虑工程实际以及可操作性,参照文献[20],以节理间距d代替RQD,更能真实反映其岩体质量及完整程度。
2 遗传算法优化BP神经网络
2.1 遗传算法与BP神经网络
BP网络属于一种多层前馈神经网络,前向传递信号,反向传递误差。每次训练预测的结果都有所差别,这是由于在选择上BP网络的参数选择具有随机性,每一次的初始值都不同导致的。并且BP网络在进化学习的过程中容易陷入局部最优,熟练速度慢,找不到全局最优值。
遗传算法包括种群初始化、适应度函数、选择操作、交叉操作和变异操作,它是一种全局搜索算法。将BP神经网络的局部搜索能力和遗传算法的全局搜索能力相结合,弥补BP神经网络参数选择上的随机性缺陷,预测结果更为精确。
2.2 寻优算法流程
基于生物进化的思想,遗传算法对解域进行遗传运算,找到最优值及对应的最优适应度值。遗传算法优化BP神经网络分为3个部分,即BP神经网络结构确定、遗传算法优化和BP神经网络预测。第一部分为,根据输入输出参数的个数来确定BP神经网络结构,进而确定遗传算法个体长度。第二部分,使用遗传算法优化参数值,种群中的每个个体都包含了一个网络所有权值和阈值,经过选择、交叉和变异操作找到最优适应度值。最后,BP神经网络预测用最优个体对应的网络初始权值和阈值赋值,训练后预测函数输出。流程如图1所示。
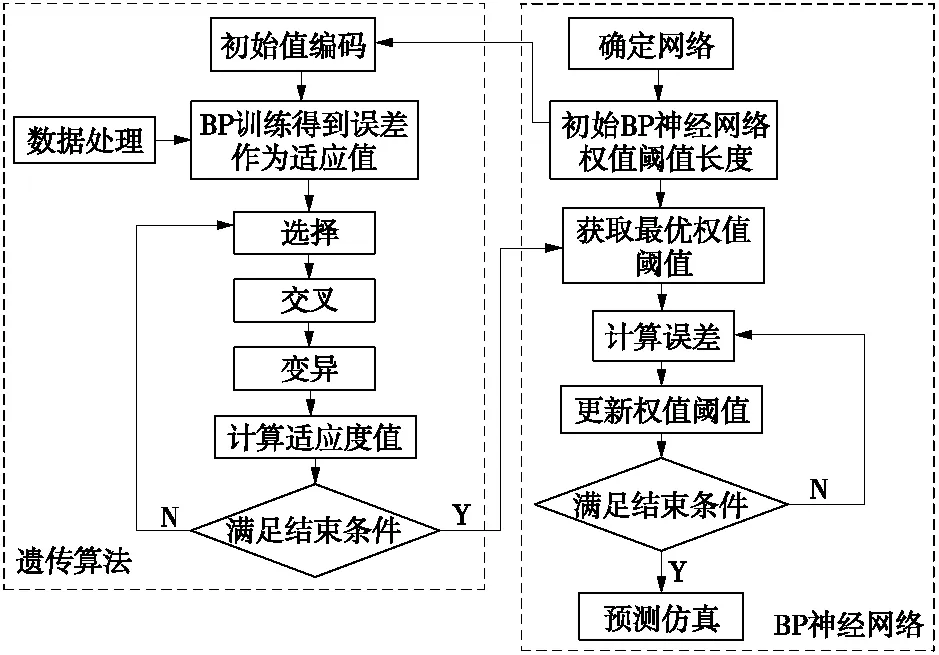
图1 寻优算法流程
2.3 算法精度检验
吴家沟隧道位于秭归县归州镇向家店村1组(吴家沟—三岔沟),距离香溪长江河口约1.7 km。线形展布,进口方向294°,出口方向32°。隧道右幅起止桩号为YK4+255~YK5+120,全长865 m;左幅为ZK4+295~ZK5+255,全长960 m。洞室净空均为9.75 m×5.0 m,隧道最大埋深约186 m。隧道左洞进口、出口位于直线段上,中间段位于R=360 m(右偏)的曲线上,纵向坡度为-2.0000%,-2.5703%。隧道右洞进口位于缓和曲线段上,出口位于直线段上,中间段位于R=560 m(右偏)的曲线上,纵向坡度为-2.000 0%,-2.570 3%。吴家沟隧道剖面如图2所示。

图2 吴家沟隧道剖面
对吴家沟右线隧道进口洞内、吴家沟右线隧道出口洞内、吴家沟隧道出口上方地表位置等进行日常监测,进而得到吴家沟进口洞内拱顶沉降监测数据、出口洞内拱顶沉降监测数据、进口洞内净空收敛监测数据、隧道出口洞内净空收敛监测数据以及通过现场点荷载试验获取的相对应的岩石强度、岩体体积节理数等影响因素所得数据。每组都将采集2000及以上数据,才能保证预测数据的准确性。通过监测数据,利用超前预测算法,观测吴家沟隧道内外有无异常情况。对于吴家沟右线隧道的预测结果需引起施工方注意,施工到达围岩变差部位,要及时调整并合理安排工序。通过监测反馈的结果,对相应的重点部位采取施工措施,保证施工的安全。
以吴家沟隧道进口洞内拱顶沉降测点监测为例,共采集2000组样本数据。其训练方法、预测结果与误差分析如下。
该函数有1个输出参数,6个输入参数,BP神经网络设置结构为6-5-1。该输入层有6个节点,隐含层有5个节点,输出层有1个节点,即有6×5+5=35个权值,5+1=6个阈值,遗传算法个体编码长度为35+6=41。一共有2000组输入输出数据,选择1900组作为训练数据,用于网络训练,100组作为测试数据。遗传算法参数设置:种群规模为10,进化次数为30次,交叉概率为0.3,变异概率为0.1。
根据遗传算法和BP神经网络,在MALTAB编程实现遗传算法优化BP神经网络算法。最优个体适应度值变化如图3所示。
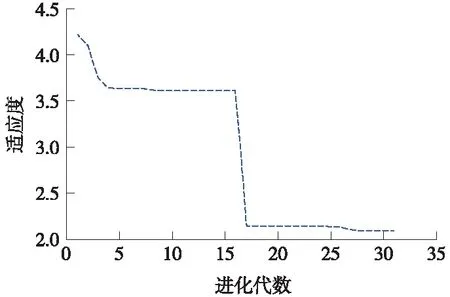
图3 最优个体适应度值
根据最优个体适应度值,得到最优参数值,即权值和阈值。把最优初始权值和阈值赋给神经网络,用训练数据训练1 000次后输出。
图4为BP神经网络训练进度。performance为网络输出误差,epoch为迭代次数,time为训练时间。gradient为梯度,validationcheck为泛化能力检查(若连续6次训练误差不降反升,则强行结束训练)。

图4 训练进度
训练结果如图5所示。
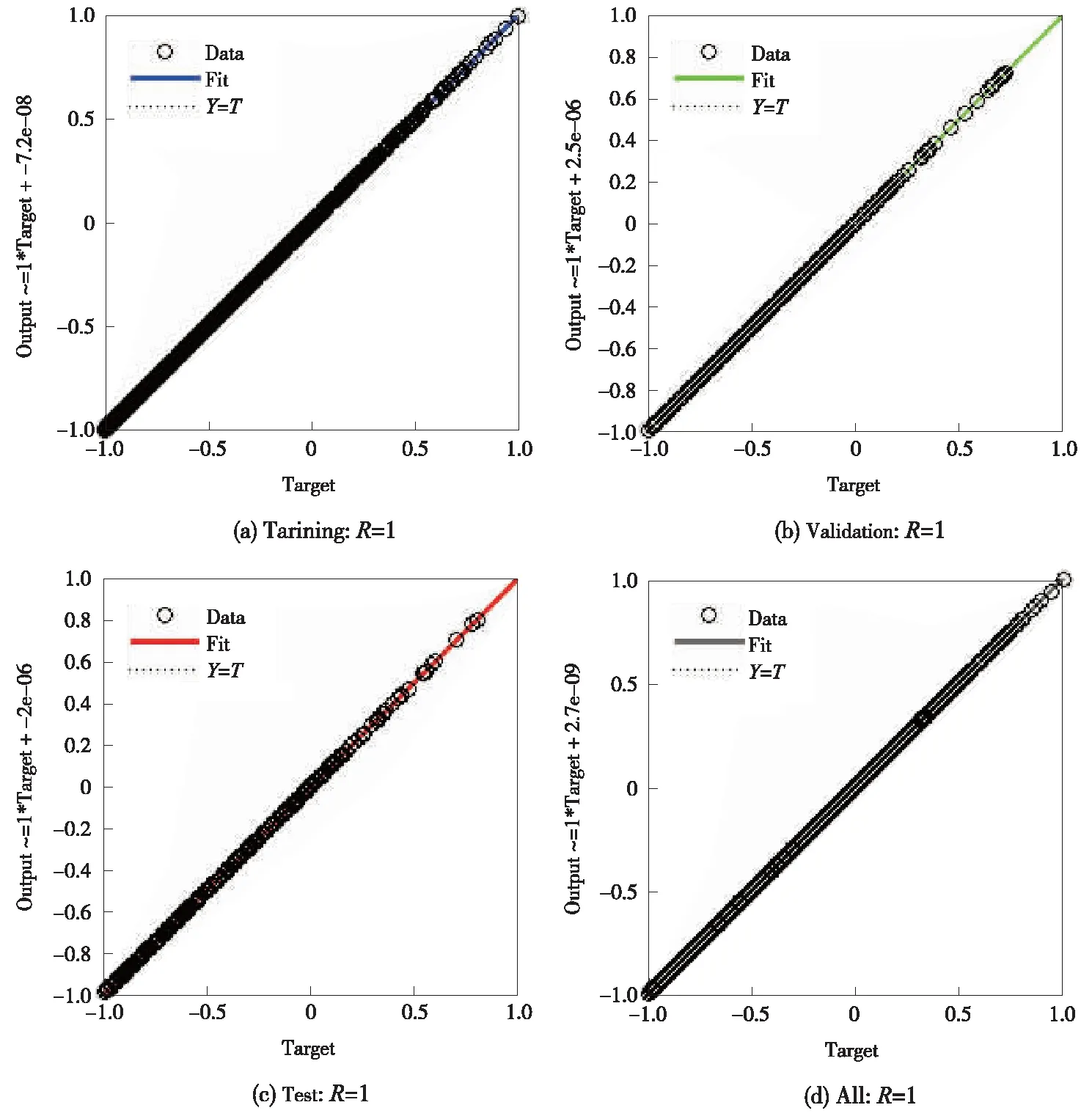
图5 预测结果
图5的横坐标为目标值,纵坐标为网络的输出。为防止过拟合,MATLAB采用的方法是把数据划分成3份,training为训练数据,validation和test分别为验证数据和测试数据。训练进行时,目标和训练(test)数据目标之间的误差会越来越小,刚开始时validation和validation目标之间的误差也会变小,可随着训练的增加,test的误差继续变小,validation的误差反而会有所上升。由于这时可能过拟合的倾向,当validation的误差连续上升6次时训练就停止了。如图5可知,4幅曲线都在对角线上,成为一个完美回归。
为表明预测方法的准确性,将优化后BP神经网络与未优化BP神经网络进行对比,100组训练数据对比误差如图6所示。
由图6可知,根据与实测进口洞内拱顶沉降测点,BP神经网络预测误差较大,而优化后的BP神经网络误差基本保持在横轴上下,误差较小,可基本反映围岩变形在空间维上的变化趋势。

图6 误差对比
3 工程应用及预测
通过遗传算法优化BP神经网络,可得到较精确的预测值。根据1 900组数据的训练与100组数据的测试,可以对隧道围岩变形值进行精确的预测。对吴家沟进口洞内拱顶沉降值进行空间维预测。通过反馈的结果,施工到达围岩变差部位,要及时调整并合理安排工序,对相应的重点部位采取措施,保证施工的安全。由于空间有限,将列举针对吴家沟进口洞内拱顶沉降值部分监测值以及空间维预测,为工程实际应用提供借鉴。
吴家沟隧道进口洞内拱顶沉降值16组自然属性监测数据如表3所示,每组数据中包含了该断面围岩体的自然属性。通过遗传算法优化BP神经网络模型,同时加以围岩的自然属性,来预测其空间维变形值。针对预测结果与实际变形沉降值进行比较,如图7所示,证明精度的准确性。
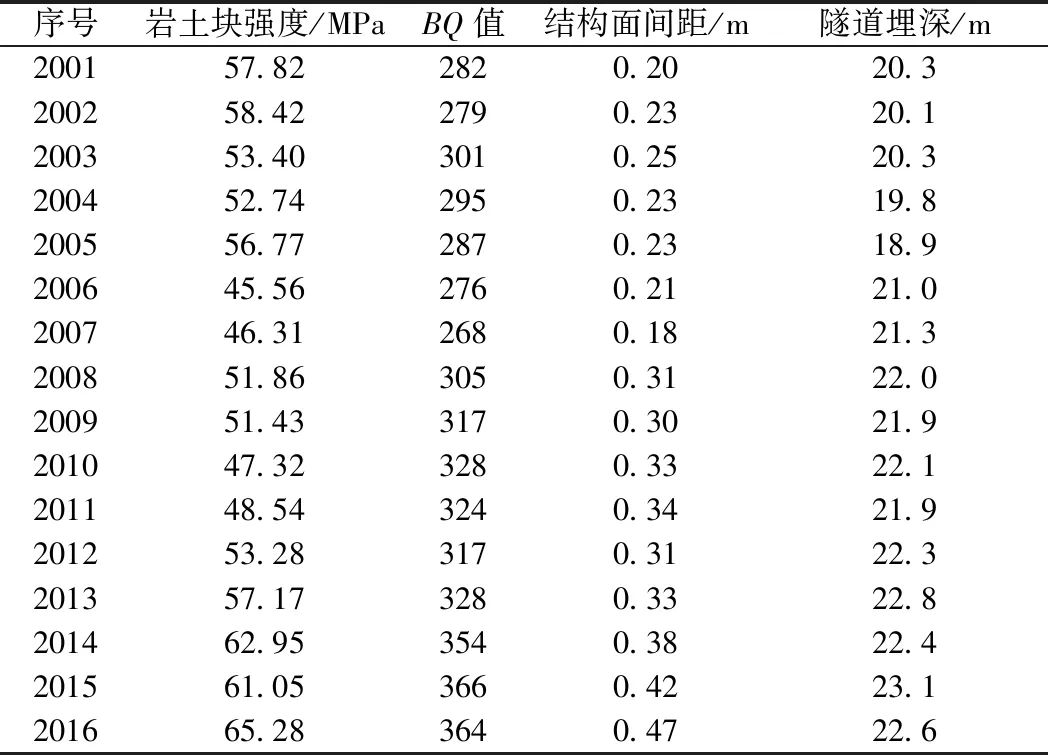
表3 监测结果
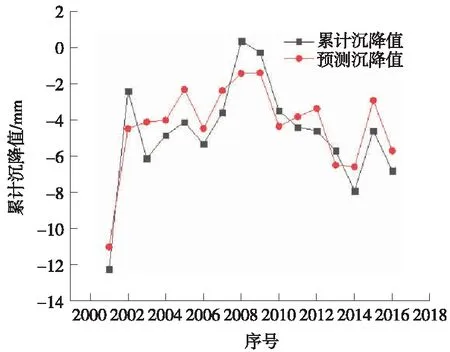
图7 预测误差
通过对吴家沟进口洞内拱顶沉降值、出口洞内拱顶沉降值、进口洞内净空收敛值、隧道出口洞内净空收敛值进行空间维预测,针对反馈的结果,在变形沉降值较大的地段,分析YK4+850~YK4+880(30 m)段围岩较当前掌子面围岩地质情况变差,岩体坚硬程度较软弱,岩体节理裂隙发育,拱部易发生掉块、坍塌,围岩稳定性较差。建议根据围岩变化调整支护措施,建议按Ⅳ级围岩施工,严格控制开挖进尺,加强支护措施。
4 结论
(1)就具体隧道而言,通过灰色关联分析,得到围岩自然属性与变形间关系的程度,可以得出影响隧道围岩变形的主要因素。
(2)从整体和局部的角度出发,用遗传算法对BP神经网络参数进行优化,将遗传算法的全局搜索能力和BP神经网络的局部搜索能力有机结合起来,弥补BP神经网络权值和阈值的随机性缺陷,预测结果更为精确,较传统预测思路具有更好的创新性。
(3)通过实例检验预测的成果,得出优化BP神经网络模型较未优化模型具有更高的预测精度及稳定性,证明该算法具有较好的优化能力,对隧道变形的预测研究具有一定的参考价值。

