地铁道岔区段道床板振动特性分析

周海洋,张校铭,郑钧元,王刘翀,赵才友

(1.高速铁路线路工程教育部重点实验室,成都 610031； 2.西南交通大学土木工程学院,成都 610031)

随着社会的发展，轨道交通的优势越来越明显，对国家经济发展发挥了很重要的作用。但是随着城市地铁的大规模兴建，地铁运行过程中产生的振动和噪声问题也越来越严重。列车运行时，会造成钢轨和道床板的振动，如果振动过大，不但会对周围居民生活及环境造成较大的影响，还会缩短道岔区段扣件和钢轨的使用寿命，进而直接影响列车的行驶安全。因此，道岔区段减振降噪设计是城市地铁面临的一个重要课题。地铁停车场咽喉区道岔较多，线路复杂，列车轮轨与钢轨相撞会产生较大激励。地铁道岔区段的振动较复杂，因此对周围居民的居住舒适度影响更大，削弱建筑的适用属性[1-2]。研究者们对道岔区段振动特性进行了大量的研究工作，得出许多很有用的研究成果，对道岔区段的减振降噪设计提供了理论指导。列车运行过程中引起的道岔段地面振动大于直线段，因此，道岔区段的减振和隔振防护很重要[3]。现阶段，国外研究者多利用工程措施改变结构本身的自振频率和结构刚度，达到减振降噪的目的，也有通过实验模拟分析列车运行时道岔区段的振动特性及传播规律[4-6]。

目前，在国内研究中，面临实地研究不足，缺乏试验数据，地铁车辆运行时振动预测模型不适用等情况[7-8]。列车通过道岔区段时，车轮和轨道的耦合振动，经钢轨传到路基，直至传递到地面；振源距离部分上盖建筑往往较近，进而导致地铁上盖建筑的振动可能超过标准限值[9-10]。某地铁车辆段的现场测试结果表明，当列车以规定速度通过时，其正上方住宅楼的振动竟高达85 dB[11]。曾志平通过建立钢轨-岔枕-桥梁弹簧-阻尼空间振动模型，分析了侧向过岔时，列车运行速度、轨下横向刚度、枕下横向均布刚度、桥墩高度对列车-道岔-桥梁系统振动的影响[12]。赵国堂运用NUCARS软件建立了高速列车通过道岔的多刚体动力学模型，研究了列车通过道岔时的轮轨系统振动特性[13]。陈丹丹等[14]提出一种基于对数功率谱标准差和顺序统计滤波的高速道岔振动信号端点检测算法，并且对道岔不同位置和不同信噪比的振动信号进行了大量的实测实验，实验结果表明了算法的有效性。伍曾等[15]通过建立仿真模型，用数值模拟的方法计算分析了道岔区轨道、车辆与连续桥梁结构的动力特性。黄辉等[16]开发了一种道岔区实时监测系统，可以实时反映列车通过道岔时钢轨的动力特性。陈漫等[17]对钢轨廓形优化与转辙器动力特性的关系进行了研究。王伟平等[18]对列车通过某无砟道岔及配套交叉渡线时的安全性和舒适性进行评价。陈小平等[19]对高速车辆与道岔空间耦合振动特性进行了研究，并得出辙叉处轮轨冲击比转辙器处剧烈的结论。王平[20]建立了道岔区内轮轨相互作用的空间耦合振动模型，分析了可动心轨式道岔与固定辙叉式道岔动力性能的差别。这些年，研究者们针对道岔区段振动特性的研究虽然比较多，但是却没有一种模型能够准确地仿真预测列车以不同速度通过道岔区段时道床板的振动特性。针对地铁道岔区段，运用有限元及动力学软件建立道岔区段振动特性预测模型。为了保证模型计算的准确性，通过了长时间实验测量，测得了某道岔区段100 m的轨道不平顺数据。将轨道不平顺数据导入到采用的柔性轨道中，运用该模型仿真计算了不同工况下道床板的振动数据，并进行了时域、频域及模态分析，准确地分析了地铁道岔区段道床板的振动特性，可以为道岔区段的减振降噪设计研究提供理论参考。

1 工程概况

1.1 模型的建立

在现有的研究基础上，对道岔区道床板振动特性进行研究。在研究过程中，建立了道岔区道床板特性仿真模型。运用有限元软件建立了长度为35.4 m的道岔区道床板，道床板厚度为0.35 m，道床板始端宽度为2.8 m，末端宽度为5.2 m。整个道岔区段道床板由两部分组成，分别是尖轨位置和心轨位置道床板，所对应的长度分别为22，13 m，两块板之间的伸缩缝宽度为0.4 m。将网格尺寸设置为0.2 m×0.2 m×0.2 m，进行六面体网格划分。在动力学软件中导入建立好的道床板模型，通过bushing力元将道岔区道床板与外部base0基础连接。列车采用的是50个自由度的多刚体车辆模型(1节车厢)。采用动力学软件中的柔性钢轨模型，将仿真计算路线长度设置为100 m，道床板之前路线设置为直线段，长度为50 m，轨枕间距设置为0.6 m，建立道岔区段列车-钢轨-道床板耦合振动模型，进行仿真计算，分析道岔区道床板的振动特性。在仿真时，将实验测得的长度为100 m的轨道垂向不平顺数据导入到柔性轨道中，提取道床板尖轨、心轨位置处的加速度变量，绘制出各自的加速度-时间图像，图1是通过实验测得的左右轨的垂向不平顺数据。利用该仿真模型模拟计算出列车以30，40，50 km/h及60 km/h的速度(4种工况)通过道岔区时道床板尖轨和心轨位置的振动加速度数据，通过时域、频域及模态分析研究道床板的振动特性。进行频域分析时，运用傅里叶转换将时域数据转换为频域数据，道床板结构噪声主要是低频噪声，即小于250 Hz，所以提取0～250 Hz范围内加速度数据进行分析。通过频域分析得出的结论，确定振动加速度对应的主频，运用有限元软件提取主频附近的模态振型，进行模态分析。

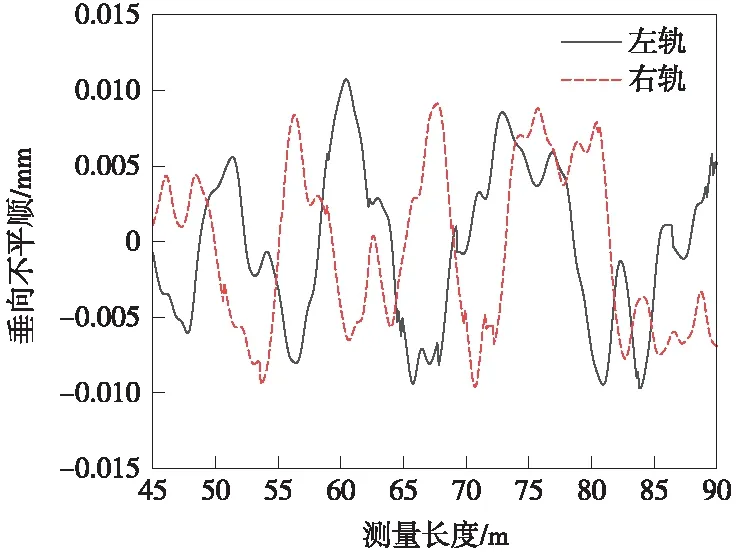
图1 道岔区段实测的垂向不平顺数据

1.2 道床板支座连接元件—bushing力元

动力学软件中用到的bushing力元，其数学模型为

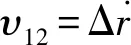
1.3 柔性轨道

柔性轨道模型是动力学仿真软件中的3D轨道模型，包括柔性轨道，紧固件，枕木和枕木基础。导轨以Timoshenko梁进行模拟，紧固件被模拟为衬套类型的特殊力量，枕木被模拟为刚体或柔性梁。若专注于研究动力学的问题，柔性轨道模型更为适合。模拟铁路轨道的模型和方法越复杂越需要更多的CPU工作量。动力学软件中柔性轨道模型计算时速度比质量轨道模型慢50～80倍。

1.4 有限元网格划分

网格划分可以理解成把一个复杂的实体模型分成若干简单的模型，而这些简单的个体之间又相互联系，相互约束，构成整个结构。求解这些简单的结构，就能得到整体的变化趋势，网格越细致整齐，结果就越精确，网格粗糙，结果就会有较大误差。对于仿真而言，网格的划分至关重要，因为网格划分尺寸将会影响钢轨扣件及bushing力元的连接。所以良好的网格划分可以提高仿真的效率、精确性，甚至直接决定了仿真是否可行。划分网格是建立有限元模型的一个重要环节，需要考虑的因素较多，工作量较大，网格数目的多少将影响计算结果的精度和计算规模的大小。所划分的网格形式对计算精度和计算规模将产生直接影响。为了使计算结果精确，方便选取节点连接扣件及bushing力元，将网格尺寸设置为0.2 m×0.2 m，图2为在仿真软件中建立的模型。

图2 仿真模型

2 数据分析

2.1 时域分析

用动力学软件仿真时，根据提取的尖轨和心轨位置道床板的振动加速度数据，绘制出相应的垂向振动加速度-时间图像，进行时域对比分析，进一步得出道床板低频振动的影响因素。

由图3可知，列车通过道岔区道床板时，随着速度的增加，尖轨位置道床板垂向振动加速度峰值越来越大。因此，列车的过岔速度会对道床板的振动产生较大的影响。列车以30，40，50，60 km/h的速度(4种工况)通过道岔区时，尖轨位置道床板振动加速度峰值分别为22.93，24.99，25.01，26.65 m/s2。道床板转辙器部位的尖轨和基本轨不密贴、水平弯曲、拱腰等都会引起较大的钢轨磨耗，所造成的轨道不平顺会对列车通过时产生的振动造成很大的影响。从所测量的垂向不平顺分析可以得出，在列车行驶至60 m左右时，左右轨所对应的垂向不平顺幅值也较大。可知该垂向不平顺对道床板的振动响应有着一定的增强作用，另外再加上第一块道床板自身尺寸较大，自身结构对振动响应也会产生较大的影响。

图4是列车通过心轨位置时，4种工况下道床板所对应的垂向振动加速度。和尖轨位置类似，列车通过道岔区道床板时，随着速度的增加，心轨位置道床板垂向振动加速度峰值也越来越大。4种工况(30，40，50，60 km/h)下，道床板心轨位置垂向振动加速度峰值分别为12.21，13.76，14.78，15.20 m/s2。整体上来看，道床板心轨位置产生的垂向振动加速度要小于尖轨位置。一方面是由于心轨位置道床板长度相比尖轨位置小很多，振动响应不如后者复杂。另一方面尖轨位置所对应的轨道不平顺要大于心轨位置，因此对道床板振动响应的增强作用要大于后者。心轨部位容易产生叉心磨、心轨裂纹及轨顶面磨耗等，所造成的不平顺对列车通过时会造成较大的影响。一方面，可以使用弹性减振材料或者吸振器等来降低道床板振动；另一方面，因为列车的行驶速度对道床板振动程度的影响也很大，所以也可以通过控制过岔速度来降低道床板振动。

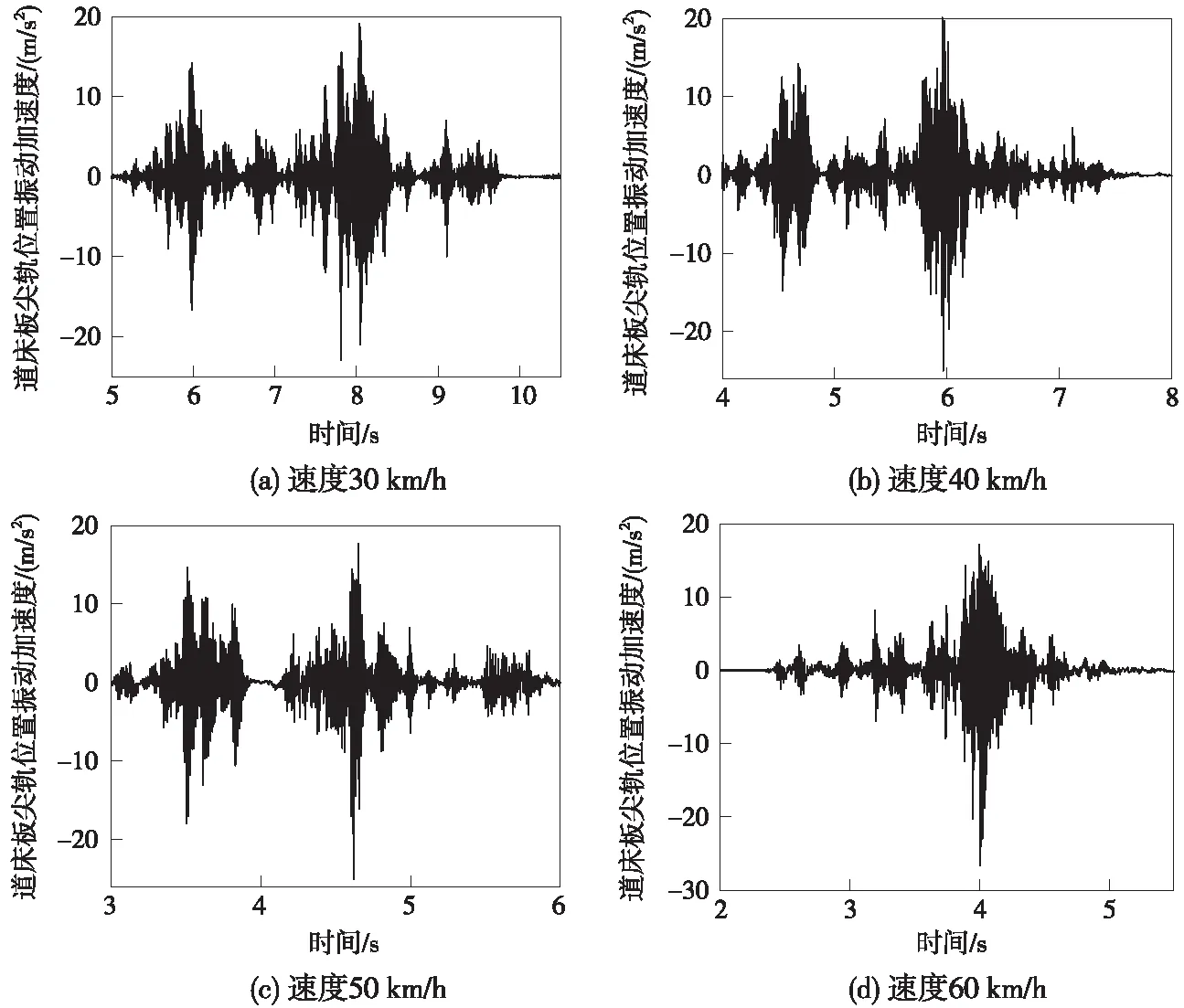
图3 道床板尖轨位置垂向振动加速度(时域)

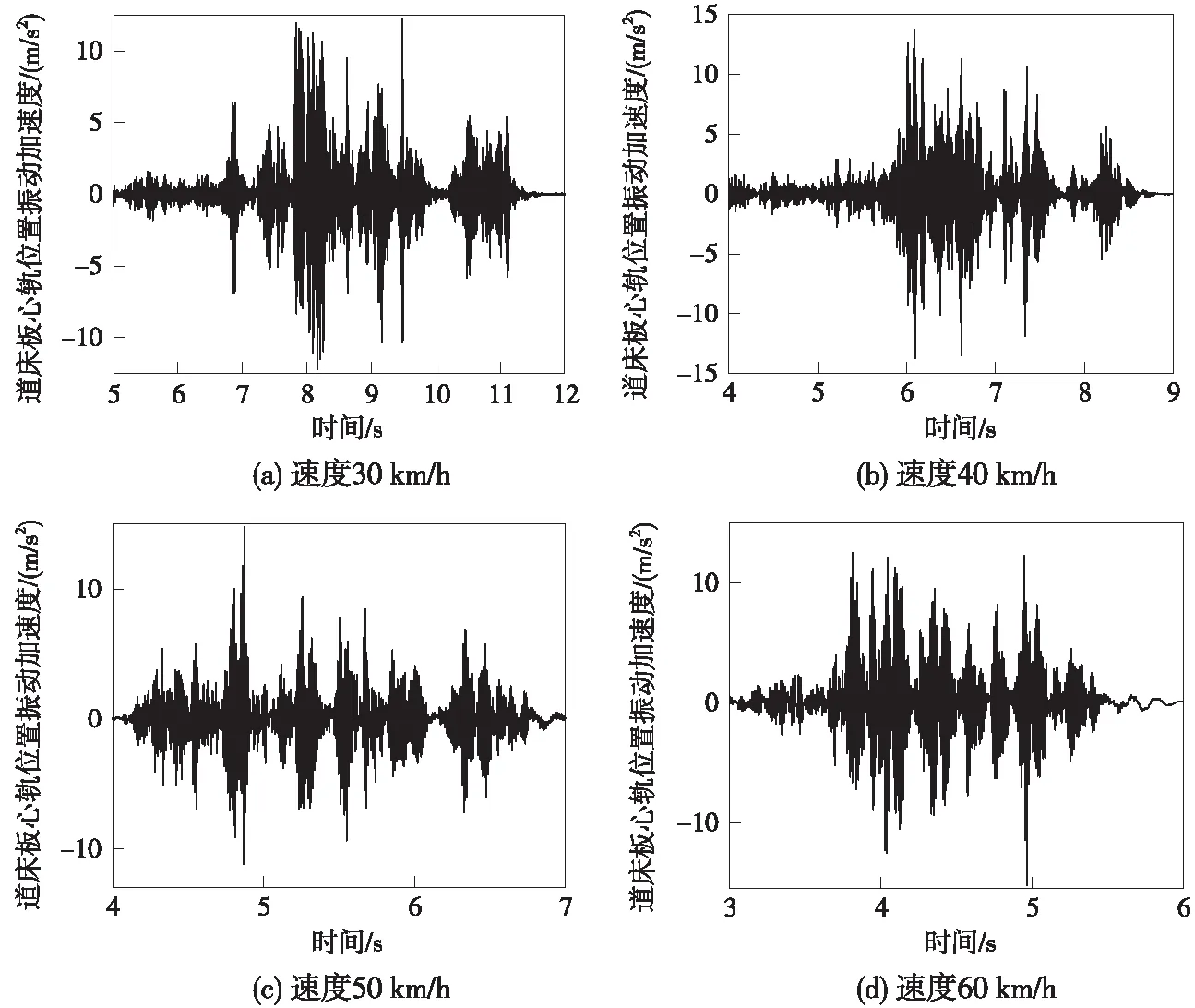
图4 道床板心轨位置垂向振动加速度(时域)

2.2 频域分析

通过傅里叶转换后，动力学软件仿真得到的时域数据转化为频域数据。由于研究的是道床板低频振动特性，所以运用绘图软件绘制了0～250 Hz范围内的振动加速度频谱图。图5和图6是列车以不同速度通过道岔区段时，尖轨和心轨位置道床板垂向振动加速度所对应的频谱图。

图5 道床板尖轨位置垂向振动加速度(频域)

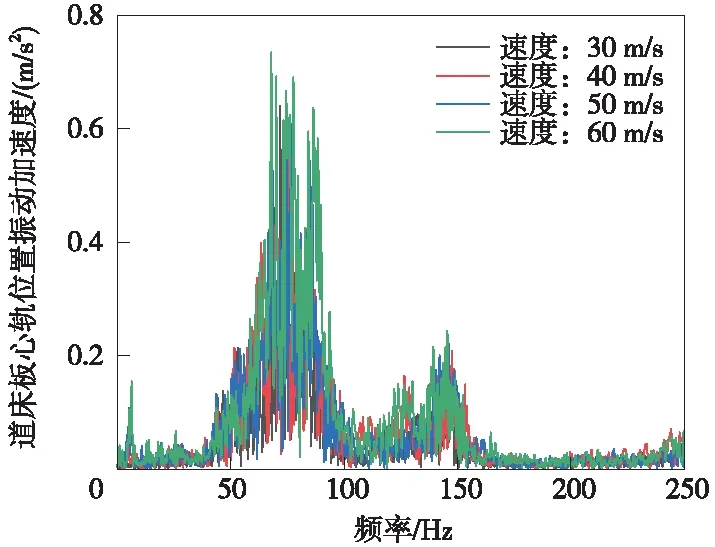
图6 道床板心轨位置垂向振动加速度(频域)

可以看出，不管是道床板尖轨还是心轨位置，对垂向振动加速度影响最大的主频都是3个，并且所对应的主频很接近。由图5、图6可以清晰看出，列车以不同速度通过道床板尖轨位置时，垂向振动加速度对应的主频都位于4，80 Hz及140 Hz附近，在80 Hz，道床板产生低频振动最大。列车以不同速度通过道床板心轨位置时，垂向振动加速度对应的主频都是位于5，75 Hz及145 Hz附近，在75 Hz，道床板产生低频振动最大。另一方面，通过两图的横向对比可以看出，列车通过道岔区段时，尖轨位置道床板的振动要大于心轨位置，由此产生的低频噪声也更大。分析其原因，尖轨对列车的行驶具有引导线路的作用，列车经过尖轨位置时，产生的冲击较大，进而使道床板产生较大振动。

2.3 模态分析

由前面的时域和频域分析可知，列车通过道岔区段时，道床板尖轨位置振动响应要大于心轨位置。二者都是随着列车过岔速度的提高，振动逐渐变大。通过频域分析，得到了道床板尖轨和心轨垂向振动所对应的主频，分别是：尖轨位置-4，80 Hz及140 Hz；心轨位置-5，75 Hz及145 Hz。为了准确分析道床板自身模态对垂向振动的影响，运用有限元软件提取道床板尖轨和心轨位置振动加速度主频附近的垂向振型图。由图7、图8可知，尖轨位置道床板在4.9 Hz处发生了1阶竖弯。因此在列车经过尖轨位置时，该振型加大了道床板的垂向振动。尖轨位置道床板在75.7，76.9，145.1，147.0 Hz处还出现了连续弯曲及混合弯曲等振型，这些都极大地增大了尖轨位置的垂向振动。当列车过岔速度提高时，这种增大效应将会变得更为明显。而对心轨位置道床板振动影响较大的振型主要是位于79.8 Hz和144.9 Hz处。在这两处，心轨位置道床板出现了连续弯曲和混合扭弯等振型，对心轨位置的垂向振动产生较大的影响。

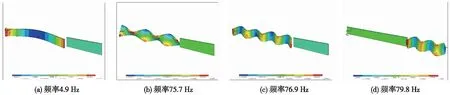
图7 道床板振型

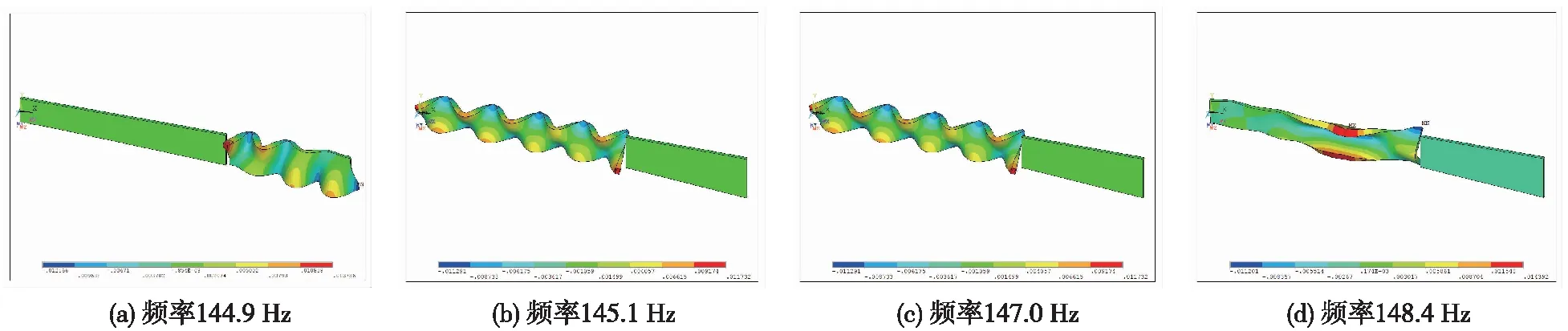
图8 道床板振型

3 结论

通过有限元及动力学软件建立道岔区段列车-轨道-道床板耦合振动模型，结合测得道岔区轨道不平顺数据，对道床板振动特性进行了仿真分析。当列车以4种速度行驶通过道岔区段时，道床板尖轨和心轨位置会产生不同的振动响应。根据所得到的仿真数据进行时域、频域及模态分析，得到了如下主要结论。

(1)相同速度下，道床板尖轨位置的垂向振动响应要大于心轨位置，并且其垂向振动加速度峰值是心轨位置的近2倍。分析其原因，一是由于运行时间较长，转辙器部位的尖轨和基本轨不贴密、水平弯曲、拱腰等导致尖轨的轨道不平顺大于心轨位置；二是尖轨位置道床板长度较长，振动响应更为复杂，列车通过时会产生更大的振动。

(2)道床板尖轨位置垂向振动对应的主频为4，80 Hz及140 Hz，在80 Hz，道床板产生低频垂向振动最大。心轨位置垂向振动对应的主频为5，75 Hz及145 Hz，并且在75 Hz处，道床板产生低频垂向振动最大。模态分析时，发现对道床板尖轨和心轨位置振动影响最大的是各阶连续弯曲和混合扭弯模态。

(3)相同条件下，随着列车通过速度的提高，无论尖轨还是心轨位置，道床板的振动响应都会逐渐增强，所引起的低频结构噪声也逐渐增大。实现道岔区段道床板结构减振，一方面可以使用减振材料，另一方面可以通过控制列车的通过速度实现减振。