基于视线角速率的自适应滑模导引规律*
田源,王俊波,宿敬亚
(1.北京航天长征飞行器研究所,北京 100076; 2.北京电子工程总体研究所,北京 100854)
0 引言
对于采用被动测量方式的导引头而言,尽管仅有视线角速率信号可测,但是末制导开始前,在其他信息的辅助下通常能够估算出导弹和目标相对距离及接近速率,即末制导的初始条件。如何利用末制导的初始条件、视线角速率信息和制导双方的相对运动规律构建有效的末制导方法是本文研究的重点。
滑模变结构控制表现出强鲁棒性,尤其是对匹配参数扰动的不敏感特性,对提高控制系统的性能十分有益[1]。但是,一般的变结构控制律是不连续的,从而不可导。控制信号的不连续是由控制律中所含有的继电控制项引起的,易形成控制信号的颤振,在实际使用中不易实现,便且影响控制系统的使用寿命。控制律所含的继电控制项一般由系统的不确定性的界来构成,而由于实际系统的复杂性,这些界往往很难获得。若控制律中的这些界取得太大,会影响控制效率;取得太小,将不能保证滑动模态的存在。自适应控制方法提供了另一种解决系统不确定性问题的有效方法,利用在线辨识,可以得到一只不确定性结构的未知参数估计[2]。但是,它对于未建模动态不具有抑制能力。文献[3-5]对滑模变结构、鲁棒控制与自适应控制相结合的一些新型控制器做了比较全面地分析和研究。文献[6-9]针对存在再入角度约束的问题研究了相关制导律,采用饱和函数或高增益函数等抑制抖振,抖振的边界均与目标的机动能力相关。文献[10-13]采用扩展状态观测器(Extend State Observer,ESO)来构建导引规律,取得较好的制导效果,但视线角速度的测量噪声给ESO及相关滤波器的设计带来一定的困难。文献[14-16]采用自适应滑模的方法通过对未知干扰上界相关的参量进行建模估计,解决存在信息误差、自动驾驶仪延时、以及终端落角约束等情况下的制导律设计问题。
本文在二维平面条件下,假设目标的机动能力上限已知,根据传统的滑模控制理论设计了攻击机动目标的制导律,在制导律中目标机动能力的上限作为继电控制项来确保滑动模态的存在。然后,通过结合滑模变结构控制和自适应控制各自的优点,利用自适应控制方法在线估计不确定性范数的上界,来达到改进制导指令的效果。最后,通过数学仿真,验证了该方法在导弹制导系统中的实用性。
1 二维运动学模型
1.1 相对运动学模型
在不影响问题研究的条件下,在二维平面下建立制导问题的描述。
如图1所示,OIxIyI为二维的惯性参考系,导弹M正在攻击移动的目标T。导弹与目标均视为质点,描述双方相对运动的状态变量为相对距离r,视线角q,导弹的速度倾角φm,目标的速度倾角φt以及导弹的飞行速度vm和目标的飞行速度vt。忽略重力的影响,弹目相对运动学关系可以描述为
(1)
(2)

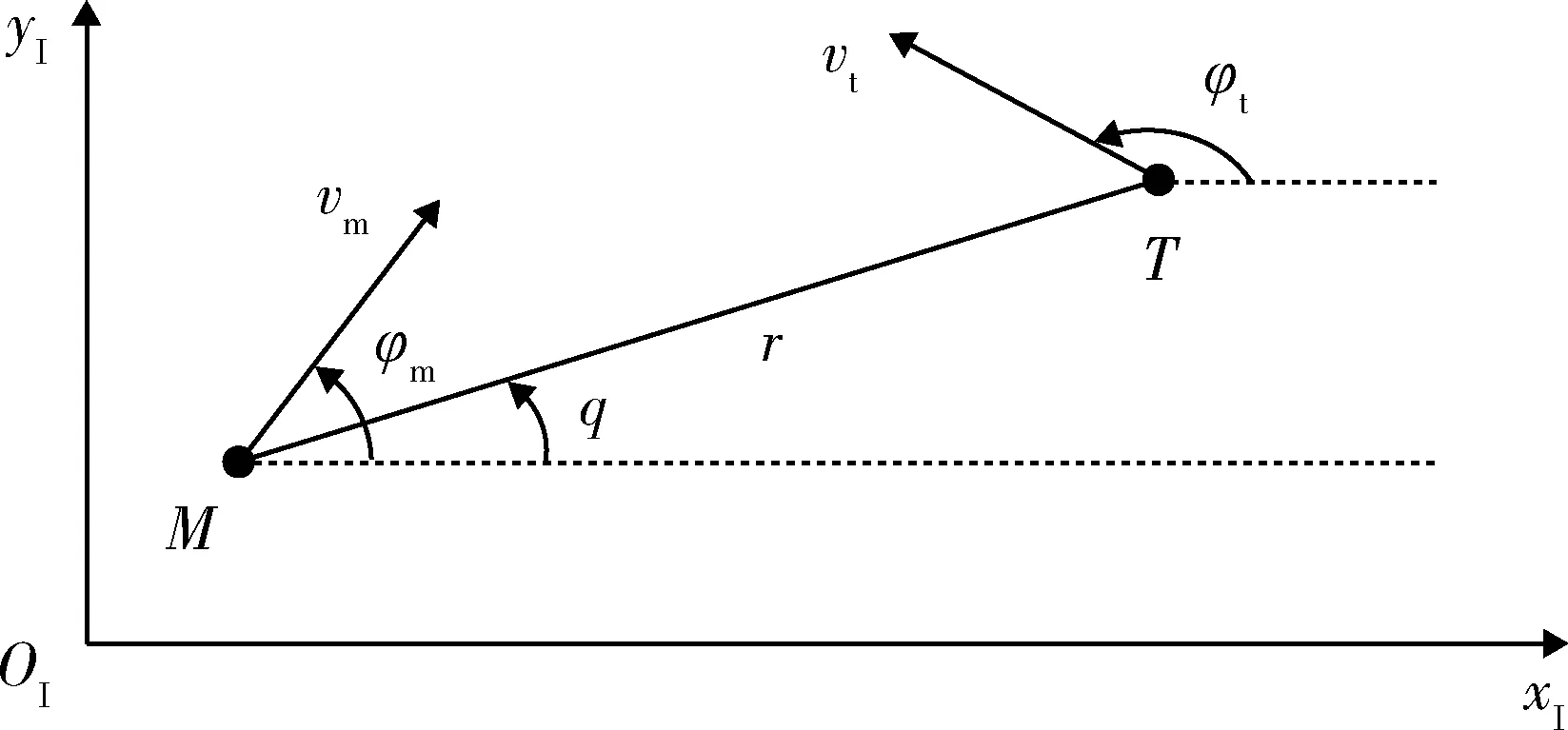
图1 二维平面上的相对几何Fig.1 Planar endgame engagement geometry
假设视线角速率可以在每一时刻被精确测量,且导弹与目标间的初始相对距离、初始接近速率及其测量误差上限已知。上述攻击条件可以表示为
(3)
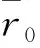
1.2 沿视线方向的运动学模型的简化
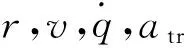
经过上面的分析,可以近似认为导弹与目标间沿视线方向的相对加速度为0,式(1)可以简化为
(4)
令z1=r,z2=v,式(4)可以写成如下形式:
(5)
根据制导初始条件(4),为式(5)给定3组初始条件(以上标来标识)来估计制导过程中相对距离r和接近速率v的界限:
(6)
(7)
(8)
这样,在条件(6)~(8)下,通过数值方式解算微分方程(5),则相对距离和接近速率的误差界限可以计算如下:
(9)
2 滑模导引规律设计
2.1 滑模制导律
基于滑模的导引规律

然后,
基于式(5)和制导初始条件(6) ~(8),可以得到如下关系:

2.2 改进的自适应滑模制导律
2.1节所提出的导引规律中含有符号函数,即以目标机动能力的上限作为继电控制项来确保滑动模态的存在。这样,制导指令中不可避免地存在抖振,本节将结合滑模变结构控制和自适应控制各自的优点,利用自适应控制方法在线估计目标机动的上界,达到改进制导指令的效果。

改进的自适应滑模导引规律


3 仿真结果及分析
本节通过数学仿真来验证提出的滑模导引规律的有效性和优越性。在仿真中,假设导弹较目标机动灵活,导弹的最大机动加速度为10g。导弹和目标的执行机构的动态特性由一阶系统来近似,执行机构的传递函数为
式中:τm=0.2,τt=0.5;amc和atc分别为导弹和目标的制导指令。


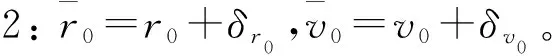
在滑模导引规律和改进的自适应滑模导引规律中,相应参数的取值为N=3,ε=8g和γ=500。制导过程的终止条件为r<300 m。假设制导过程中目标在惯性直角坐标系下采用如下阶跃形式的机动:
滑模导引规律(sliding mode control guidance,SMCG)和改进的自适应滑模导引规律(improved sliding mode coutrol guidance,ISMCG)的制导效果与比例导引规律(propotional navigation guidance,PNG)和修正的比例导引规律(augmentde proportional navigation guidance,APNG)进行比较。如图2,3所示,比例导引规律并不能很好的攻击机动目标;尽管滑模导引规律能够抑制视线角速率,但由于符号函数的使用而使制导指令产生抖振;改进的自适应滑模导引规律对视线角速率的抑制作用和修正的比例导引规律相似,但是与修正的比例导引规律不同的是改进的自适应滑模导引规律不需要知道目标的加速度。

图2 情况1下的仿真结果Fig.2 Simulation results in case 1
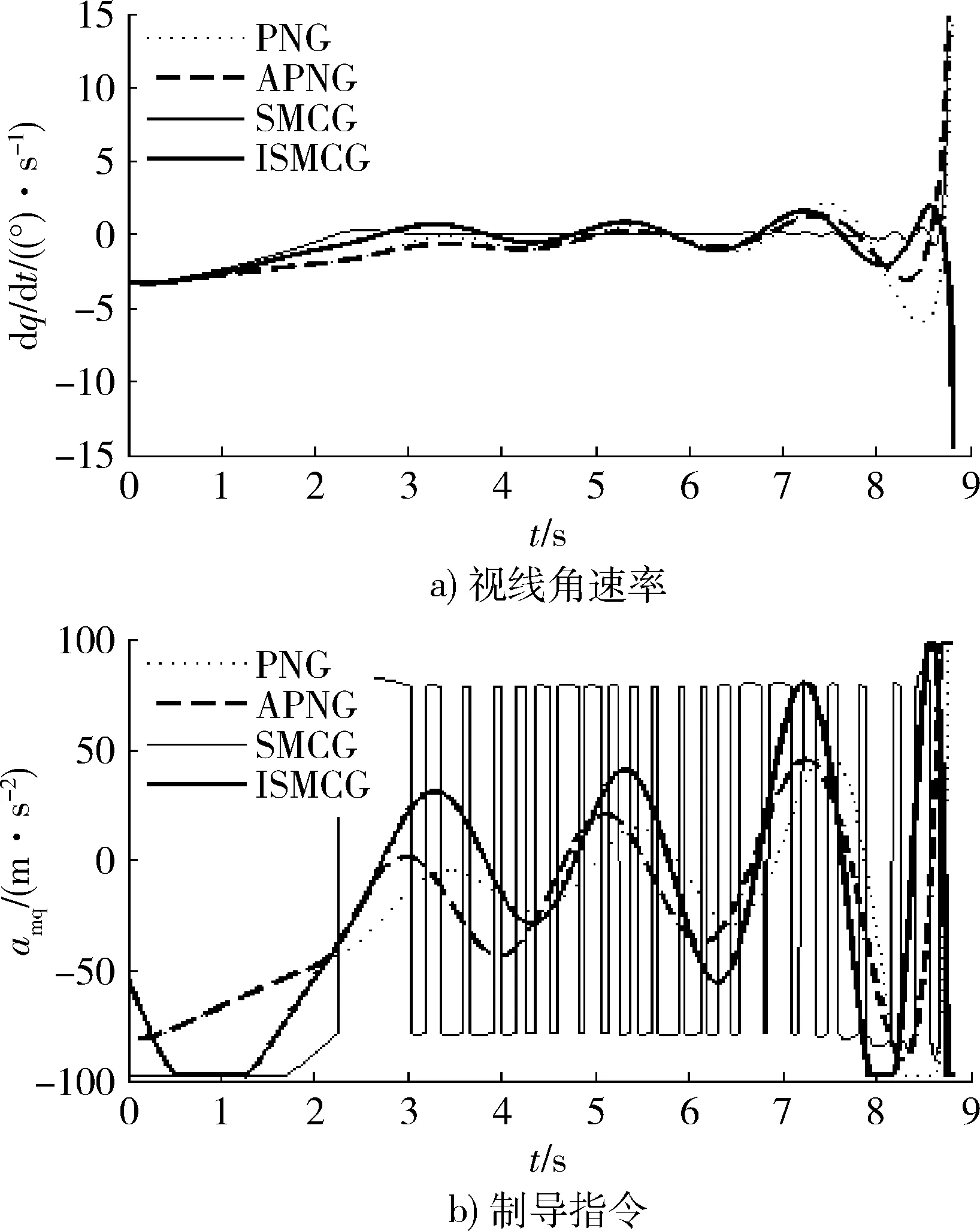
图3 情况2下的仿真结果Fig.3 Simulation results in case 2
4 结束语
当视线转率可测量、初始相对距离和初始接近速率已知时,本文首先基于滑模控制理论设计了一种制导规律,然后针对制导指令的抖振问题提出了一种自适应滑模导引规律,该导引规律在目标加速度未知的情况下可以达到扩展比例导引规律的攻击效果。

