基于集中参数模型的垂直振动压路机动力学分析

白 帆，王 扬，李韶华，秦 浩

(1.石家庄铁道大学交通运输学院，河北省石家庄市北环东路17号 050043； 2.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄市北环东路17号 050043)

作为材料压实作业最重要的工程装备垂直振动压路机已广泛应用于机场、港口、道路、市政建设等工程。基于振动理论对其动力学行为进行深入研究，阐明相关参数对压路机振动状态的影响，不但有利于提高压实效率，而且是推进振动压路机智能化发展的必然需求。

集中参数模型是机械系统动力学分析的传统工具。多年以来，基于该方法的压路机振动分析取得了大量成果。Yoo等[1]建立了二自由度的质量-弹簧-阻尼系统模型，认为压路机振幅、频率及压实速度等参数对振动压路机压实效果产生重要影响。李世平等[2]建立了三自由度压路机动力学模型，在考虑土体参振的基础上，分析了振动压路机工作参数的取值范围。黄登等[3]基于Simulink建立了振动压路机的七自由度模型，对驾驶室和驾驶座椅进行了动力学分析。严世榕等[4]针对压实过程中土体的塑性变形，建立了压实过程中的非线性动力学模型，分析了激振力、土体刚度等参数的改变对压路机振动规律的影响。何建和等[5]建立了具有二级减振系统的三自由度非线性动力学模型，运用MATLAB对模型进行了仿真，揭示了系统混沌运动的动力学机理。

综上，集中参数模型总体上可分为线性和非线性两类。前期研究表明：在压实过程初期，土体塑性变形显著，非线性更为适用；在压实过程末期，土体主要表现为弹性体，采用线性模型可较好地实现压路机系统的动力学分析。文中考虑土体表面的不平顺，针对压实过程末期的振动压路机，建立了二维动力学模型，分析了机架与振动轮的响应，并讨论了参数变化对压路机动力学行为的影响。

1 考虑地表激励的垂直振动压路机集中参数模型

1.1 模型的建立

针对压实末期的土体，建立振动压路机的二维线性集中参数模型，如图1所示。将机架和振动轮简化为集中质量，分别记为m1，m2；将机架与振动轮之间的橡胶减振器简化为无质量的线性弹簧和阻尼，弹簧刚度和阻尼系数分别记为k1，c1；考虑土体的参振效应，将其简化为“质量-弹簧-阻尼”模型，相应参数依次记为m3，k2，c2；考虑到压实过程中土体表面的不平顺，将地表高程y0假设为正弦函数，即

y0=B0sin(2πvt/L0)=B0sinΩt

(1)

式中：B0为土体表面不平顺幅值，L0为土体表面不平顺波长，v为振动压路机行驶速度，Ω为地表激励频率，t为时间。

则地表不平顺产生的激励F0可表达为

(2)

振动轮激振力F1为正弦函数，表达为Fsinωt，即振幅为F，频率为ω。

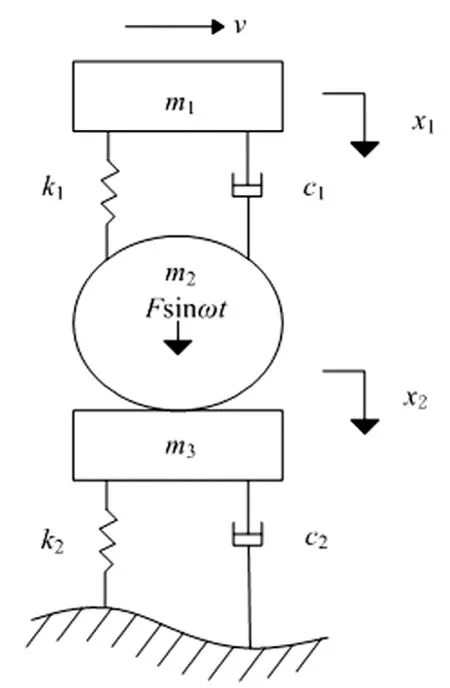
图1 二维振动压路机-土系统动力学模型Fig.1 Two-dimensional dynamic model of vibratory roller-soil system

将压路机机架的位移记为x1。不考虑压路机的跳振工况，即振动轮与土体始终保持接触，则m2和m3可作为一个整体，将其位移记为x2，则系统的动力学方程可表达为

(3)

式中：P为激振力，是F0和F1的叠加，P=F0+F1。

1.2 模型的求解

式(3)为线性微分方程，根据振动力学基本理论，可首先求得F0和F1单独作用下的系统响应，再经过线性叠加即可得到P作用下的系统响应。

根据复数运算规则，F0作用下系统位移响应为：

(4)

其中，Δ(Ω)=

将式(1)代入式(4)中，则x1可表达为

B1sin(Ωt+φ1)

(5)

同理，x2可表达为

(6)

在F1作用下，系统的位移响应为

(7)

根据线性叠加原理，P作用下系统的位移响应：

(8)

1.3 模型的适用范围

将振动轮与土体的作用力表示为Fs，通过对振动轮与土体进行受力分析，可将Fs表达为

(9)

显然，Fs≥0时振动轮与土体相互接触，否则即意味着压路机发生了跳振。文中针对非跳振工况进行建模，但模型可对Fs<0时的系统响应进行分析。尽管此时的模型已经脱离实际意义，不能作为压路机振动分析的定量参考，但相关研究表明，这种条件下的理论分析仍对压路机动力学行为演变趋势的一般性讨论具有参考意义[6]。

2 模型的应用

2.1 F0作用下的系统响应

对Sakai SV 510D振动压路机的动力学响应进行分析，部分模型参数如表1所示。

表1 部分模型参数

根据文献[7]和[8]，取m3=0.3m2，v=1m/s，B0=0.015m，基于式(5)、式(6)可求得P=F0时，系统的幅频响应，如图2所示。

图2 F0作用下系统的幅频响应

图2表明，当Ω接近0时，系统处于准静态阶段，B1和B2均接近地表高程的振幅B0。随着Ω的增加，B1和B2呈现出不同的特征。作为二自由度模型，系统存在2阶固有频率，分别为31，92rad/s。机架的振幅B1对低频激励更加敏感，在Ω=31rad/s时，达到最大值0.35m。而高频激励对B1的影响有限，即使在Ω=92rad/s时，B1仅为0.02m，仅是第一阶共振条件下的5.71%。随着Ω的进一步增大，B1逐渐趋于0。振动轮振幅B2则对高频激励更加敏感，在第一阶、第二阶共振时的振幅分别为0.03，0.10m，后者是前者的3.33倍。随着Ω的进一步增大，B2逐渐衰减至小于B0，衰减速度明显小于B1。

文献[6]显示，在堆石料或土石混合料的压实过程中，地表激励信号十分复杂，加速度和位移信号中会出现多次谐波和超谐波成分，使压路机很容易发生跳振，因此，为保持压路机的使用寿命，应将地表激励的频率限制在合理区间。对于本文中所讨论的Sakai SV 510D振动压路机，计算结果表明，Ω等于4.3，128rad/s时，有Fs=0，为避免跳振，应将地表激励频率限制在[0，4.3]和[128.8，+∞)范围。

2.2 F1作用下的系统响应

F=65000N时，系统的幅频响应如图3所示。

图3 F1作用下系统的幅频响应

对比图2和图3可以发现，F0和F1作用下系统响应的总体规律基本相同，这是由系统的固有属性所导致的。图3表明，当激振力频率ω=0时，振幅为F作用下的静变形，此时X1，X2基本相等，约为1.39×10-3m。产生一阶共振时，X1=3.23×10-2m，X2=2.70×10-3m，X1是X2的11.96倍。当31rad/s<ω<40rad/s时，机架会吸收部分振动轮的振动，甚至会使X2小于静变形。二阶共振时，X1=1.30×10-3m，X2=9.40×10-3m，X2是X1的7.23倍。

综合考察F0和F1作用下的系统响应，为了在保证驾驶舒适度的条件下产生较大Fs，显然应选择接近二阶固有频率的激振力。

2.3 F0和F1的复合效应

对于Sakai SV 510D振动压路机，取B0=0.015m，Ω=π/4rad/s，F=65000N，ω=60rad/s，由式(4)、式(7)、式(8)可求得在F0，F1，P作用下系统的位移响应和加速度响应，如图4、图5所示。

对于本文中所建立的线性模型，在P作用下系统的响应是F0和F1单独作用下系统响应的叠加，图4直观反应了这一力学规律。由于Ω和ω未导致系统共振，在本例给定的系统参数下，系统的位移响应主要由F0主导。图4中，在P作用下系统的位移振幅分别为0.015m和0.0154m，接近F0单独作用下的振幅为0.015m。与图4中(a)和(c)的振幅相比，F1单独作用下的系统振幅在量级上有显著差距，仅为1.24×10-5m和4.13×10-4m。

尽管F0对系统的位移响应占有支配地位，但其对系统加速度响应的影响非常有限。图5显示，F0单独作用下，压路机机架和振动轮的加速度响应均为9.30×10-3m/s2，F1单独作用下，加速度响应则分别为0.44m/s2和14.66m/s2，显然，加速度响应由F1主导。对于基于振动压路机的智能压实工艺，加速度是反映压实质量最为重要的参数，因此，在地表激励不显著的条件下，对系统动力学行为的分析可以不考虑F0的影响。

(a)F0单独作用下的响应 (b)F1单独作用下的响应 (c)P作用下的响应图4 给定参数条件下系统的位移响应Fig.4 Displacement response under given parameters

(a)F0单独作用下的响应 (b)F1单独作用下的响应 (c)P作用下的响应图5 给定参数条件下系统的加速度响应Fig.5 Acceleration response under given parameters

3 结论

文中通过将地表不平顺假设为正弦函数，建立了振动压路机的二维线性集中参数模型，推导了模型的解析解，并结合具体参数对压路机的动力学行为进行了分析，得到如下结论。

(1)对于振动压路机的二维线性集中参数模型，系统存在2阶固有频率。一阶共振时，机架振幅达到最大值，二阶共振时，振动轮振幅达到最大值。为了在保证驾驶舒适度的前提下产生更好的压实效果，应选择接近二阶固有频率的激振力。

(2)在一定条件下，地表激励有可能对系统响应产生显著影响。在堆石料或土石混合料的压实作业中，应保证压实体表面具有较好的平整度，以便将地表激励的频率控制在合理范围。

(3)在压路机未发生跳振的常规工况下，地表激励对系统加速度响应的影响远小于振动轮激振力，在对压路机系统动力学行为进行分析时可以不考虑其影响。