闭(附)合三角高程路线严密平差方法的研究

杜彦君

(西安科技大学 测绘科学与技术学院，陕西 西安 710054)

随着高精度全站仪、特别是高精度智能全站仪的广泛使用，三角高程测量的优越性正逐步体现[1-2]。相较于传统水准测量，三角高程测量具有操作简便、作业效率高等特点，特别在高海拔、地形起伏较大、跨河等条件复杂情况下，三角高程测量优点更为明显[3-4]，已大量应用于工程测量和大地测量中[5-7]。

现阶段，对三角高程测量成果的评价，仍以水准测量为标准，以保障三角高程测量观测精度达到相应等级水准测量要求的研究成果居多，主要集中在完善三角高差计算式[8]、改装仪器设备[2,5-7]、改进观测方法[9-11]等几个方面；而三角高程网平差计算方面的研究相对较少，有：以三角高差为观测值，以水平距离的倒数定权进行条件(或间接)平差的传统方法[12]；以斜距和天顶距为观测值，采用验前估计法定权进行间接平差[13]；以水准高差、三角高差为观测值的高程混合网间接平差[14]。

闭(附)合三角高程路线为三角高程路线最常用的布设形式，传统的平差计算[12]采用仿水准路线形式，按高差闭合差反符号与距离成正比例的关系进行分配，求高差改正数[1]，这种平差方法简单易于理解，但定权不合理[15]，在理论上有缺陷；采用文献[13]方法进行平差计算，理论严谨，结果正确、可靠，但计算繁琐、且闭(附)合三角高程路线采用条件平差更为简单、快捷。因此，本文根据条件平差原理，在合理确定观测高差权的基础上，推导出严密的高差改正数计算式与高程中误差计算式。

1 改正数条件方程

如图1所示一附合三角高程路线，A、B为已知高程点(已知高程分别为HA、HB)，点1，2，3，…，n-1为待定高程点，各测段观测高差为hi(i=1，2，3，…，n)。

图1 附合三角高程路线

按条件平差[12]，附合三角高程路线有1个附合条件方程：

AV+W=0

(1)

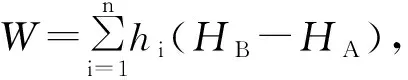
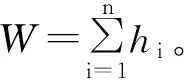
2 观测值权阵的确定

2.1 对向法测站观测高差的权

如图2所示，采用对向法观测Z1、Z2两点之间的高差。在Z1点安置仪器，测出Z1至Z2的高差h12；将仪器安置Z2点，测出Z2至Z1的高差h21。忽略球气差与垂线偏差的影响[7]，则Z1、Z2两点间对向法测站观测高差为：

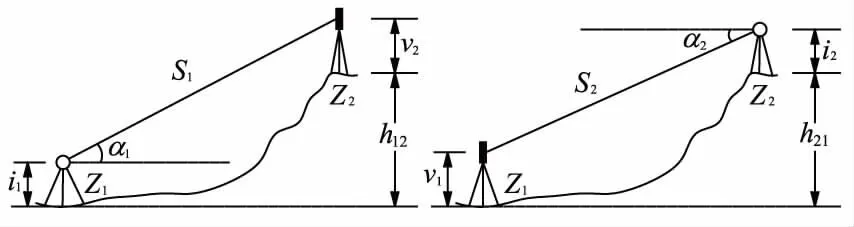
图2 对向法观测三角高程测量

(2)

式中，S为斜距；α为垂直角；i为仪器高；v为棱镜高。运用误差传播定律，忽略mi和mv[1]，并顾及到S1≈S2=S、α1≈-α2=α、mS1=mS2=mS、mα1=mα2=mα，得：

(3)

式中，mS为测距中误差；mi为垂直角中误差；ρ=206 265″。据文献[15]，全站仪在设计时，测距和测角的精度一般遵循等影响的原则，有：

(4)

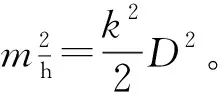
(5)

式中，c为任意常数；D为Z1、Z2两点间水平距离。

2.2 中间法测站观测高差的权

如图3所示，采用中间法观测Z1、Z2两点之间的高差。在Z1、Z2两点的中间位置M处安置仪器，测出M至Z1的高差hMZ1，测出M至Z2的高差hMZ2。忽略球气差与垂线偏差的影响[7]，则Z1、Z2两点间中间法测站观测高差为：

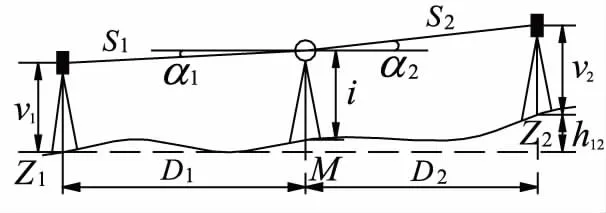
图3 中间法观测三角高程测量

(6)

运用误差传播定律，忽略mv[15]，并顾及到mS1=mS2=mS、mα1=mα2=mα，得：

(7)

(8)

式中，c为任意常数；D为Z1—M—Z2的水平距离，D=D1+D2。

2.3 测段高差观测值的权

如图1所示，设第i测段共观测了mi个测站，则该测段的高差观测值为：

运用权倒数传播定律[12]，考虑到各测站观测高差之间相互独立，并顾及式(5)或式(8)，可得测段高差观测值的权为：

(9)

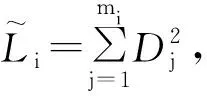
(10)

2.4 三角高程路线的观测值权阵

由式(9)并顾及各测段高差观测值之间相互独立，可得图1所示三角高程路线的观测值权阵为：

(11)

3 平差及精度评定

3.1 平差值计算

(1)高差改正数

按条件平差[12]，有N=AP-1AT、K=N-1W、V=P-1ATK，顾及式(1)、式(11)，则得图1所示第i测段高差观测值的改正数为：

(12)

(2)高程平差值

如图1所示，i点高程平差值为：

(13)

3.2 精度评定

(1)单位权中误差

按条件平差[12]，单位权中误差计算式为：

(14)

式中，n为观测值个数；t为必要观测值个数，即待定高程点个数。

(2)高程平差值的权

如图1，由式(13)，可得i点高程平差值的权函数式为：

(15)

式中，fT=[1 … 1 0 … 0]；

按条件平差[12]，有：

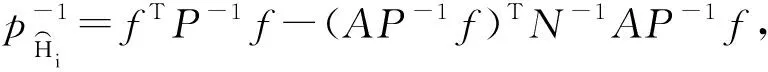
(16)

(3)高程平差值的中误差

按条件平差[12]，图1所示i点高程平差值的中误差如下。

(17)

4 结 论

(1)依据权的定义，运用误差理论，得出三角高程路线高差观测值的权与测段各测站距离的平方和成反比的结论，定权公式严密。

(3)无需列立条件(或误差)方程、权函数式以及法方程、协因数阵的解算等，避免了复杂、繁琐的计算，计算效率高。