基于通用性软件的车载开关磁阻电机仿真实验方法

栾 茹， 邓冉冉， 张 然

（1.北京建筑大学电气与信息工程学院，北京100044；2.建筑大数据智能处理方法研究北京市重点实验室，北京100044）

0 引 言

在教育部提出2035年实现教育强国的大背景下，电气工程及其自动化专业的本科教学，除了基本的必修教学环节外，还应该设置选修的创新型课程。根据电气工程及其自动化专业面向的研究与就业的领域，电动汽车驱动系统是一个典型的能体现出创新性特征的教学内容之一，且这部分教学内容适合于在具备一定动手实践条件的实验室内实施教学过程，需要配置电动汽车驱动电机及其控制的整套实验系统，这就对开设电气工程及其自动化专业院校的实验室建设提出了更高的要求。目前驱动电动汽车最理想的电机有两种，一个是永磁电机，一个是开关磁阻电机（Switched Reluctance Motor，SRM），而对于未来的电动汽车驱动电机，为了摆脱对永磁材料的依赖，人们将关注的焦点不断地投向开关磁阻电机［1］。车载开关磁阻电机的控制，是保证电动汽车合理可靠运行的充要条件，而控制离不开合理的建模，特别是对于像开关磁阻电机这样具有强非线性因素的控制对象［2］，其建模与控制问题解决起来难度大，始终是电力拖动与控制领域的研究热点［3］。

研究SRM及其驱动系统的方法有两种，一种是实验法［4］；另一种是仿真方法。实验法耗时费力［5］，投入经费很大，在不确定电机结构参数的情况下，有很多实验模型缺乏制作的依据［6］，且类似于磁场分布、脉动磁阻转矩等数据，直接测量的可操作性很差［7］，不具备普遍推广性。仿真方法［8］不需要耗费大量的制作经费，若仿真理论成熟可靠，可以很方便地输入不同的电机结构参数来使用，得到若干种设计与控制方案［9］，从中进行比较，具备适用性与推广性，是研究开关磁阻电机的首选方法。针对开关磁阻电机数学模型的强非线性，目前最有效的仿真方法是有限元法［10］。但传统的有限元数值计算的专业性很强，本科生在短时间内很难上手，且在固定激励源的情况下，只能获得静态的磁链、转矩、电流等输出量的数值解，还无法满足仿真法需要具备的通用性与实时动态仿真的性能。

Infolytica是解决电磁设备及其系统工业设计问题的通用软件，具备通俗易懂的参数输入界面，学生即使不熟悉有限元数值计算也能够上手操作，其后台运算主要是建立在电磁场数值计算的基础上，可以实现包括耦合运动过程的瞬态场在内的各种电磁过程的实时仿真，克服了传统有限元法的局限性，具备通用与实时动态特性。但这种对非线性数理方程的实时动态仿真需要借助外围电路提供动态激励源，Infolatica软件本身不具备搭建各种复杂控制电路的功能。鉴于此，本文将Infolytica软件包中的MagNet软件与Matlab中的Simulink仿真平台结合起来，利用Simulink搭建转速、电流闭环控制电路［11］，将输出结果作为动态激励施加到MagNet建模里，实现对车载开关磁阻电机驱动系统的合理仿真［12］。将该仿真方法形成实验指导书，与两种仿真软件一起安装到实验室电脑内。

1 Magnet软件建立的SRM模型

1.1 SRM的数学方程

SRM定子第k相线圈的电路方程［13］如下：

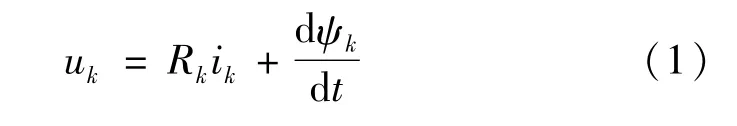
式中：uk为施加到第k相定子线圈的相电压；Rk为第k相定子线圈的电阻；ik为第k相定子线圈的瞬时电流；ψk为第k相定子线圈的磁链。设SRM驱动部分的主电路直流侧激励电源为E，采用常规传统的换相方法，则单相定子电路对应的开通、关断的激励方程为：

式中：θ为转子位置角；θon与θoff分别为开通角和关断角。随着电动汽车的起动、加速、稳速、减速、停止，要求车载SRM的转速随之发生相应的变化，因为直流侧激励电源为E常数，则SRM调速的效果只能靠开通角θon和关断角θoff来实现［14-15］。由式（2）可见，不同的θon与θoff组合对应着不同的激励源相电压uk的变化周期，则每一相电路方程式（1）在不同变化周期激励源作用下，也要产生不同的电磁场分布，可见，在电动汽车的整个行驶过程中，车载SRM内电磁场分布是实时动态变化的过程，不能简单采用固定激励源的有限元法进行仿真［16］。

1.2 SRM的动态有限元计算模型

本文以一台三相12／8极SRM为例来说明动态有限元仿真过程，其具体参数见表1，该电机是后续实验系统中的实际电机，将这些参数输入到Magnet里就可以快速建模。为了能够将动态激励源实时施加到SRM有限元计算模型上，本文选择全域建模法，即不考虑模型的对称性，将SRM的整个定子、转子作为求解域进行有限元数值计算，在MagNet软件中的具体实现见图1。

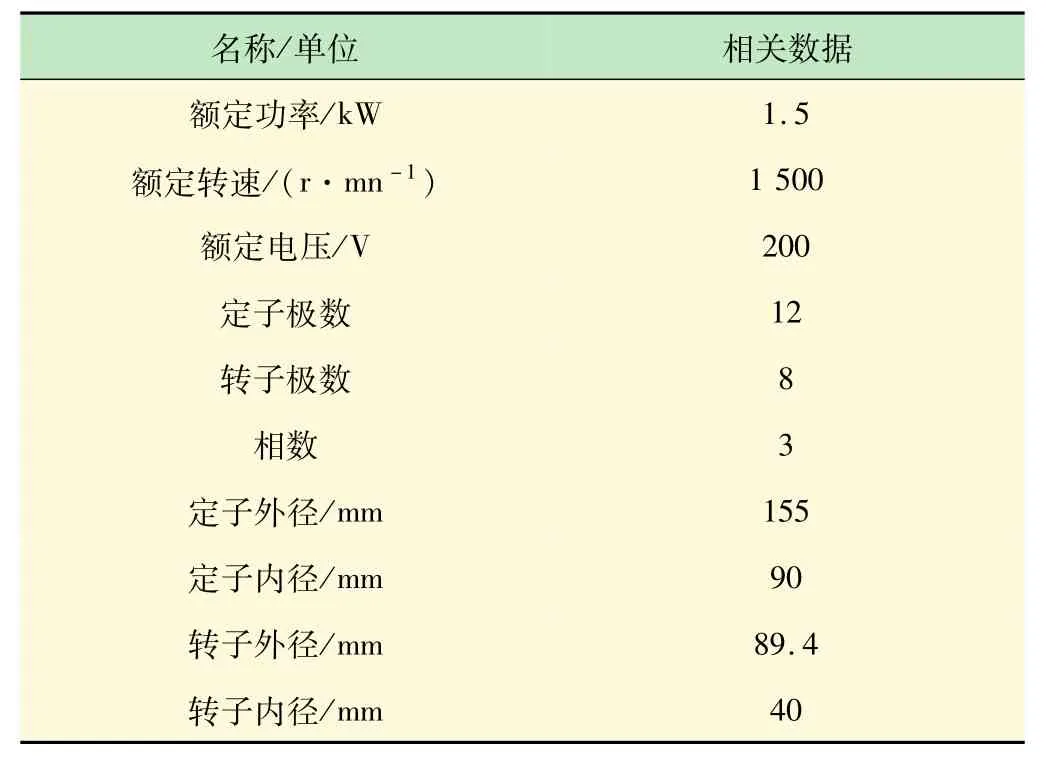
表1 三相12／8极开关磁阻电机结构参数

图1 在Magnet软件中建立的SRM模型

对图1中定子各相绕组施加周期性的电压斩波源，需要借助Simulink搭建外围电路，即让有限元计算过程中的各种数据在这两种软件之间传递，Infolytica软件包为此提供了专门的内置插件，Magnet Plug-in，将该插件与Infolytica、Matlab一起安装在同一个访问路径上，则MagNet软件生成的有限元模型，作为一个仿真模块，出现在Simulink的库里，如图2所示。有了这样的结合，将MagNet有限元模型视作Simulink中的一个工具箱，完全可以按照Simulik思维模式搭建仿真电路，下面以最简单的SRM电流斩波控制为例，介绍仿真过程。利用Simulink库里各种电路模块，搭建出一个典型的SRM电流斩波电路，该电路的输出施加到Magnet有限元模型上，如图3所示。从逻辑关系来看，代表SRM功率开关电源的模块“converter”经过电流斩波后，通过6个电压端子输出电压激励信号，这些信号是根据SRM运行过程中的θon、θoff，以及电流斩波控制等要求，综合判断合成的动态电压信号，施加到MagNet有限元模型的输入端“V1”“V2”“V3”上，相当于SRM的三相电源电压施加到图1所示的有限元求解域中的三相定子绕组上，只要这三相电源电压是动态激励信号，相应的图1中所示的有限元求解域的计算结果也是实时动态输出的瞬态电磁场结果，因此，运用图1中的有限元求解域及图3中搭建的控制电路，可以准确模拟出SRM的起动过程，如图4所示。

图2 Simulink中的Magnet模块

图3 两种软件结合下的SRM动态有限元计算模型

图4 SRM动态有限元计算结果中的起动位移

2 结合复杂控制算法的车载SRM的仿真

图1中用MagNet建立的SRM有限元模型的计算数据不仅可以直接输出，而且还可以用于BP神经网络训练，将有限元数据进行非线性映射，以构造出复杂的控制算法。下面仍以表1所列的三相12／8极SRM为车载电机与BP神经网络、转矩分配函数、开关角的模糊控制等复杂控制算法相结合，运用MagNet与Simulink两种软件进行仿真，构造出具备转速、电流闭环控制的车载SRM驱动控制系统。

2.1 MagNet有限元数据的神经网络建模

与其他驱动电机一样，对车载SRM转矩的控制，仍需要通过定子电流来实现。由图1中建立的SRM有限元模型，经过数值计算可以得到该SRM的磁链数据，ψ（ik，θ），为了实现对定子电流ik的控制，需要将磁链数据映射成定子电流数据。根据SRM电机的结构及工作原理，显然这种映射是强非线性的，目前解决这种强非线性问题的最有效方法之一是神经网络法，本文采用其中最简单的BP神经网络构造由磁链数据到电流数据的非线性映射，即：

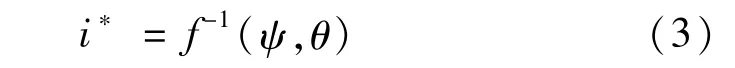
这一过程是在Simulink仿真平台上实现，然后再将这个过程进行封装，如图5所示。

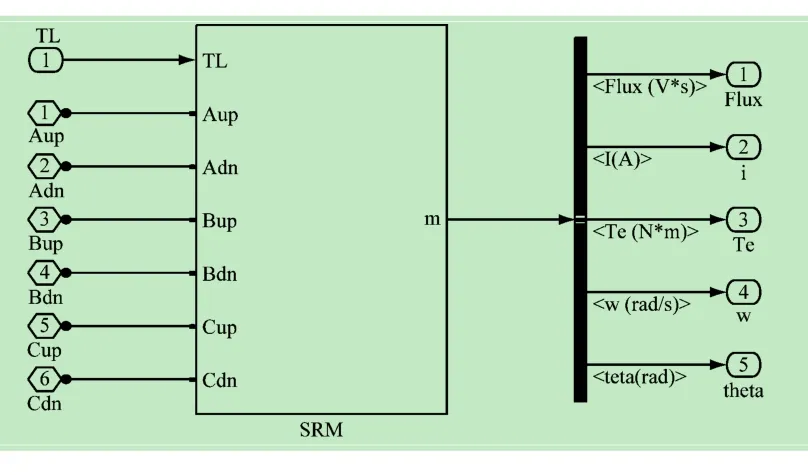
图5 对BP神经网络建模的封装

图5中输入端的“1”～“6”，对应的是图3中功率开关电源模块“converter”的6个输出端，并与其相连，图5中的输出端“m”是经过BP神经网络训练的瞬态电流数据、磁链数据、各相瞬时转矩数据等，有了这样的模型才可以用Simulink平台搭建模糊开关角与转矩分配函数控制的电路。

2.2 基于模糊转矩分配法的车载SRM驱动系统控制的仿真

结合了模糊开关角与转矩分配函数法，本文在Simulink中搭建了车载SRM的转速、电流双闭环的控制电路，如图6所示。给定转速与SRM实际转速构造出转速外环，转速调节器输出，作为期望转矩，与经过模糊开关角模块优化后的SRM θon、θoff，以及转子位置角一起输入到转矩分配模块TSF中，该模块的输出端T为SRM三相绕组的期望转矩，三相绕组期望转矩通过i（T，θ）查表模块后输出期望电流，期望电流与利用BP神经网络建模的SRM模块输出的反馈电流做差，送入滞环控制模块，实现电流闭环控制。该双环控制电路的输出，作为功率开关电源模块“converter”的控制信号，决定了该开关电源哪一相导通、哪一相截止，进而决定了施加到包含BP神经网络的SRM模块上的三相电压激励源，保证了图6所示的结合了Simulink控制电路的SRM有限元计算的实时动态性。

图6 SRM双闭环控制系统的仿真模型

3 车载SRM的仿真结果及验证

针对图6搭建的SRM双闭环控制系统仿真模型，将其中的电流滞环宽度2Δh设为0.6 A，给定转速nref＝650 r／min，起始负载转矩TL＝6 N·m，在0.2 s突加负载至TL＝10 N·m，对上述工况进行仿真，仿真结果首先用Simulink平台采集，如图7所示。

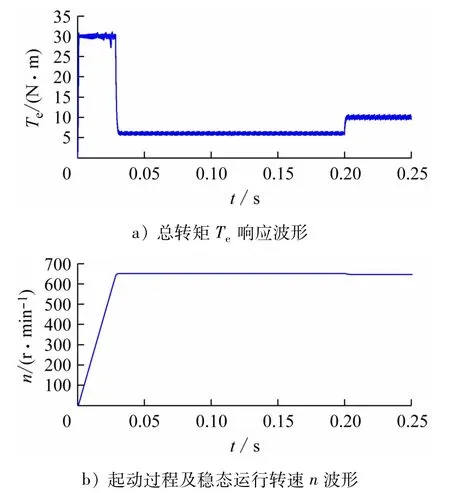
图7 车载SRM的Simulink仿真结果

由图7可见，SRM起动后能迅速达到给定转速650 r／m，且转速波形较为平稳，说明系统响应快且运行稳定，同时受到模糊开关角与转矩分配函数控制，使得转矩的脉动得到明显约束，三相叠加转矩的总和基本上保持恒定值，达到了减小转矩脉动效果。在0.2 s突加负载扰动时，转速略下降1.8 r／min，仍然保持稳定，可见系统鲁棒性较好。证明图6中Simulink控制电路输出的动态电压激励信号是合理的，且该动态电压激励源能够及时施加到MagNet有限元求解域里，进而获得合理的车载SRM动态有限元计算结果，可见由这两种软件联合构建的仿真模型是正确的。

对于车载驱动电机，最关键的性能是转速与转矩间的输出特性。以往，电机转速与转矩的输出特性很难用Matlab软件单独来实现仿真，而Infolytica软件提供了这样的计算功能，只要在Infolytica软件里实现的有限元计算是耦合了电机运动过程的瞬态场计算，则该软件能够很方便地将各转速阶段的电磁转矩结果记录下来，并以图表的形式展示。在图6中，用Simulink搭建的双闭环控制电路，体现了运用BP神经网络、模糊控制与转矩分配函数法等复杂控制算法调节SRM从起动到各个行驶转速运行的过程，该Simulink控制电路为Magnet软件里的SRM有限元计算提供了瞬态场激励源，只要调节转速给定，相应的该车载SRM仿真系统可以输出与给定转速基本一致的实际转速，该调节过程的转速与转矩输出特性的整个计算结果由Infolytica软件提供，如图8所示。

图8 转速与转矩输出特性的仿真结果

由图8可见，SRM起动阶段，转矩基本上保持在最大值并恒定，即SRM工作在恒转矩区，保证车载电机能够以最大加速度快速起动电动汽车，当转速大于额定值1 500 r／min，SRM处于高速运行阶段，转矩随着转速的增加呈现下降趋势，即工作在恒功率区，保证车载电机在输出额定牵引功率的同时定子电流不过载，工作在合理的功率密度下，显然这样的输出特性十分符合电动汽车所要求的驱动性能。

为了验证上述仿真方法的正确性，本文利用图9所示的实验系统对表1中所列的SRM进行了转速与转矩之间关系的负载实验。该实验系统主要包括被测的三相12／8极SRM、控制器、联轴器、磁粉制动器、WLK程控电源、信号采集等，利用磁粉制动器产生负载扭矩，通过联轴器施加到SRM上，利用WLK程控电源调节磁粉制动器的激磁电流，调节其产生的负载扭矩，该WLK程控电源具有RS-232（或定制RS-485）串行接口，可与信号采集分析仪通信，将所施加的负载数据通过信号采集分析仪检测出来，利用仿真器将图6所示的SRM双闭环控制仿真系统源程序代码调试通过后下载到控制器（在图9中，控制器与SRM连接在一起，图中没有单独显示控制器）里，利用数据采集分析仪还需要记录SRM的输入电压、输出电压、输出电流、转速等。由于SRM输出的是脉动性很强的磁阻转矩，对用扭矩传感器测量转矩的结果造成很大的干扰，误差很大，为此，本文采用等效计算法加以解决。实验时采用的SRM电源电压为额定电压200 V，设定磁粉制动器的激磁电流为0.1 A，将给定转速逐渐增加，采集该SRM电机定子相电流、相电压、转速、负载扭矩等实验数据，利用式（1）计算出该电机的磁链，再通过该SRM的磁化曲线查到与当前时刻的磁链和定子电流相对应的磁共能，根据

式中：Te为SRM输出转矩的瞬时值；W′为磁共能；θ为转子位移角；i为定子相电流。

在线性假设下，可以推导出计算SRM输出转矩平均值

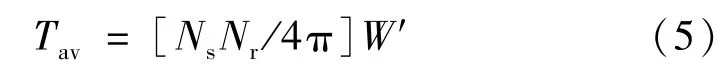
式中：Ns为定子极数；Nr为转子极数。再利用式（5）计算结果作为该SRM的输出转矩平均值的实测值。

图9 SRM系统实验平台

本文选取了3个给定转速的输出转矩平均值的仿真与实验结果，列于表2中。由表2可见，实验结果与仿真结果基本吻合。

表2 仿真结果与实验结果的比较

从Simulink与Magnet输出的结果都说明，联合这两种软件用于车载SRM的仿真可以实现对该电动机运行期间有限元瞬态场的实时计算，模拟出车载电动机行驶过程中的输出特性，这对于学习、理解、研究电动汽车驱动系统十分重要。

4 结 语

SRM的合理仿真问题历来是业界的研究热点，而车载SRM及其驱动系统的仿真实验问题则是业界的研究难点。本文从仿真实验方法的通用性与合理性出发，结合了通用性强的两种软件，Infolytica与Matlab，利用Infolytica软件包中MagNat提供的瞬态场有限元计算功能解决SRM建模的强非线性问题，利用Matlab软件中Simulink平台搭建的控制电路解决瞬态场计算需要的动态激励源，同时将控制车载SRM运行的复杂控制算法用Simulink控制电路实现，只要给电气工程及其自动化专业的本科生简要讲解有限元数值计算知识及详细讲解SRM的结构与工作原理，这些学生可以很方便利用该仿真实验方法中的Magnet来设计车载SRM结构、利用该仿真实验方法中的Simulink来设计控制算法，保证了该仿真实验方法的通用性，不必再依赖硬件实验设备来搭建车载SRM驱动控制系统，节省了实验教学成本与实验室空间资源。本文结合了一台具体的车载SRM，阐述了该仿真方法的理论依据与实现过程，仿真结果证明该方法不仅合理、可靠，而且具备实时动态性。因此，无论是从通用性还是从实时性来评价，本文提供的仿真方法十分符合车载SRM驱动系统的要求，可以作为电动汽车用驱动系统研究的理论分析的工具。