基于控制点网格优化的航拍图像拼接算法
石祥滨 贾贺林
1(辽宁大学信息学院 辽宁 沈阳 110000)2(沈阳航空航天大学信息学院 辽宁 沈阳 110000)
0 引 言
随着时代的发展,图像处理的相关成果已经逐渐应用到人类生活的方方面面,而图像拼接作为图像处理中的重要内容,受到了研究人员的广泛关注。随着无人机等航拍设备的普及,对航拍图像的处理逐渐成为研究的热点。在航拍图像拼接领域,对图像进行网格化划分并进行网格优化已经成为图像拼接的重要手段之一[1-2]。为了解决航拍图像拼接中的误匹配和重影问题,本文提出一种基于控制点进行网格优化的图像拼接方法,对无人机拍摄的航空图像,使用拼接算法形成更大视角,更广范围的图像,因此对拼接过程中的精度有很严格的要求。
航拍图像拼接过程主要面临两个挑战:图像配准和图像融合。配准就是通过对待拼接图像进行变换,使其和参考图像处于统一的坐标系中;融合就是将两幅甚至多幅图像中的重叠区域进行合成,目的是实现图像的无缝拼接。文献[3-4]提出的Auto Stitch算法是应用于opencv和photoshop中的拼接算法,但是Auto Stitch需要满足不同图像的重叠区域位于同一平面和尺度,因此在拼接过程中会导致拼接精度跟随图像尺度变化产生较大波动。为了提高全局对齐能力,文献[5]提出一种SVA算法,提供了一种通过局部网格的仿射变换来完成图像的全局对齐的方法。根据SVA算法的基本思想,文献[6]提出了APAP算法,将图像区域划分为密集独立的网格,实现图像在局部和整体上同步变换,提高了视差图像的鲁棒性。由于缺乏配准阶段的平滑约束,文献[7]改进Seam-driven算法对拼接缝隙优化,通过图像自然形状约束,最大限度保持图像自然状态的形状控制算法。文献[8]在2014年提出了SPHP(Shape-Preserving Half-Projective)的网格变换方法,将图像区域分为重叠区域,过渡区域和非重叠区域,并在不同区域进行对应的图像变换以提高拼接精度。文献[9]在2015年提出了AANAP(Adaptive As-Nature-As-Possive)方法,在图像网格的划分过程中将图像的局部映射和全局相似性变换相结合,重叠区域的过渡更加平滑,但在图像边缘容易产生畸变。图像拼接过程中对图像精度的要求很高,而航拍图像的规模大,场景中目标小,提取特征点和计算图像矩阵都比较复杂,因此不仅需要在拼接中提高图像精度,更要考虑算法的执行效率。
针对航拍图像拼接过程中出现的问题,本文在特征点检测阶段使用了LIFT[10]特征点学习模型,通过学习模型得到的特征点更加丰富准确,使用RANSAC[11]方法得到更好的特征点匹配结果,图像配准阶段使用全局网格和控制点结合最小二乘网格约束[12]的方法进行优化,最后使用加权泊松融合进行图像融合得到拼接结果。通过LIFT特征点解决航拍图像中特征点数量稀疏,匹配精度不高的问题,在图像配准过程中使用网格变换对重叠区域进行平滑,最大限度地降低重影误差,使过渡区域自然平滑。最后在融合阶段中使用加权泊松融合,平滑细化图像重叠区域的拼接缝隙,形成最终的拼接结果。
1 算法主要思想
本文的图像拼接算法首先使用LIFT学习模型检测提取出图像中的特征点信息,并对特征点进行匹配,然后使用RANSAC进行特征点的筛选,从而得到图像间特征点的对应关系,在匹配的特征点中筛选控制点信息,首先剔除位置独立的特征点,然后剔除周围比较稀疏的特征点,最后根据步长对控制点数量进行调整。控制点的筛选取决于特征点的密集程度和均匀分布。根据筛选得到的控制点和特征点生成网格,同时使用最小二乘网格约束对网格进行优化调整,建立拼接误差方程,通过求解最小化拼接误差方程完成图像的配准,最后使用加权泊松融合[13]消除拼接痕迹,从而得到更加准确的拼接结果。本文算法流程如图1所示。
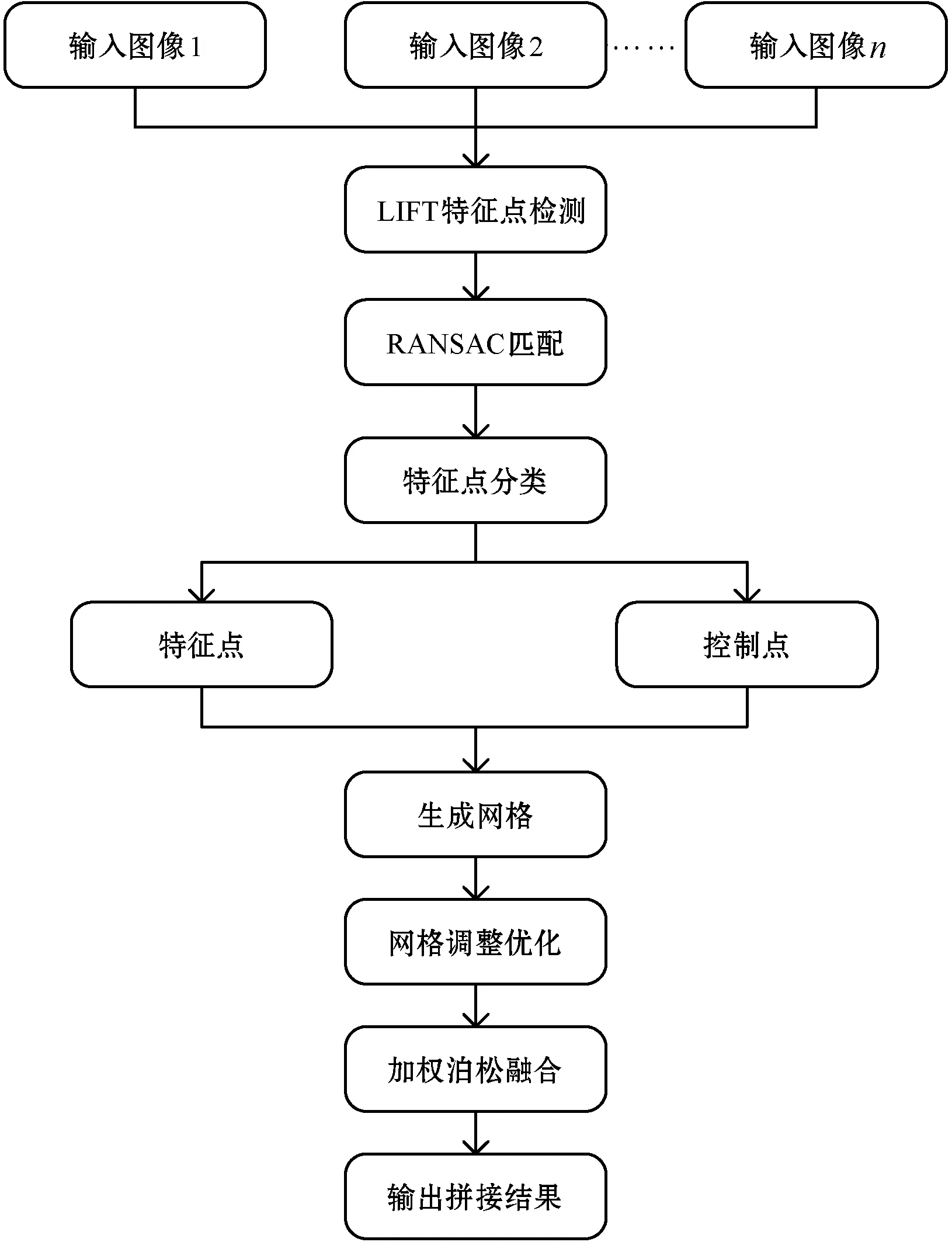
图1 航拍图像拼接算法流程图
2 特征点检测与匹配
本文使用LIFT(Learned Invariant Feature Transform)特征点学习模型进行特征点的检测,LIFT特征点学习模型是基于一种全新架构下的深度学习模型,主要包含3个部分:特征点检测DET[14]、方向估计ORI[15]和特征点描述子DESC[16]。每一部分都基于卷积神经网络,使用Spatial transformer networks[17]完成各部分的转换连接,最后学习得到特征描述子。LIFT特征点检测的算法描述如算法1所示。
算法1 LIFT特征点检测算法
输入:图像中的图像块P
输出:潜在特征点描述子向量集D={d0,d1,…,dn}
1.S
//P的得分图
2. 潜在特征点集kp[(x1,y1),…,(xm,ym)]
//对S使用NMS
3. for eachkpdo
4. 以kp为中心的图像块p
5. ROI层计算p的方向θ
6.pθ
//通过θ旋转后图像块p
7.d
//DESC层计算pθ
8. adddtoD
9. end for
10. returnD
通过算法1对图像提取特征点信息,可以进一步得到匹配后的特征点信息,与SIFT算法的特征点匹配效果进行比较,LIFT算法得到了数量更多的特征点匹配信息。
3 特征点分类与控制点生成
为了提高航拍图像拼接的精度,本文主要使用最小二乘网格进行图像配准中的网格调整,使用最小化能量方程进行网格优化。网格优化之前首先要对特征点进行分类,筛选出可以生成网格的控制点。本文通过对特征点进行分类的方法筛选出控制点,具体过程如算法2所示。
算法2 生成控制点
输入:特征点位置信息集合fp{(x1,y1),…,(xn,yn)}
输出:控制点位置信息集合cp{(x1,y1),…,(xm,ym)}
1.sumlfp←0,h
//给定步长
2. forfpfromi+50 ton-49
3. forjfromi-50 toi+49
4.d(fp[i],fp[j])
//计算两点之间的距离
5.aved←sum(d)/100
6. ifd(fp[i],fp[j])>aved
7.lfp[j]←1,sumlfp++
8. end if
9. ifsumlfp>80
10.Lfp[i]
//1
11. elseLfp[i]
//-1
12. end if
13. end for
14. end for
15. 利用Lfp[i]的值进行第二步筛选
16. 根据筛选结果重新排序fp{(x1,y1),…,(xp,yp)}
17. forkfor 1 top
18. ifk%h
//0
19. addfp[k] tocp
20. end if
21. end for
22. renturn cp
本文的控制点生成建立在特征点十分密集的基础之上,航拍图像在重叠区域超过30%的情况下即可满足控制点生成条件。通过第二步对特征点设定标记值,将位置相隔较远的特征点也就是位置较为独立的特征点筛除。接下来对点信息相对稀疏的特征点进行筛除,尤其是临近节点中独立特征点较多的特征点,保留特征点密集的位置信息。最后对控制点的数量进行控制,通过设定步长,保留图像位置信息较为均匀的特征点作为控制点。
本文通过特征点的筛选,可以得到10%~20%左右的控制点信息,控制点的数量受图像视角以及图像重叠区域大小的影响,对控制点数量的控制有助于简化后续的配准计算。
特征点的筛选比较如图2所示。

图2 特征点和控制点比较
4 网格调整与优化
4.1 最小二乘网格
最小二乘网格是在拉普拉斯网格[18]的基础上提出的,又被称为全局的拉普拉斯光顺网格。在网格调整过程中给出了最小二乘约束方程,通过约束方程将网格调整问题转化为求解最小二乘最优解问题。

(1)
式中:系数wij的总和为1。
(2)

(3)
对上式中的系数还需进行归一化系数处理,最小二乘网格中的拉普拉斯系数可以通过一个n×n的矩阵来表示:
(4)
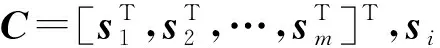
(5)
(6)
将上述方程转化为最小二乘中求解最优Vi的问题,可以表示为:
(7)
构造的最小二乘网格和添加控制点的最小二乘网格的示意如图3所示。
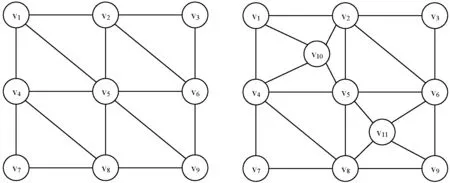
图3 均匀网格和加入控制点网格
假设生成了3×3的均匀网格,网格顶点v1至v9,网格中存在两个控制点分别为v10和v11,网格的生成方式如上,拉普拉斯坐标矩阵也从9×9变化为11×9,同时矩阵b中增加两行,对应控制点的坐标信息,对生成的超定方程组求最小二乘解就能得到图像变换矩阵。
4.2 网格优化
网格优化的问题可以分为四部分:局部配准阶段、全局配准阶段、平滑阶段和最终调整阶段[20]。本文使用I1、I2、I3分别表示输入图像、预拼接图像、拼接完成图像。本文算法主要改进了平滑阶段的误差方程,使用控制点结合最小二乘约束进行误差计算,完成配准优化。
在局部配准阶段中,p′表示特征点p在预拼接图像I2中的对应特征点,p″表示特征点p在拼接完成图像I3中的对应特征点,V′表示预拼接图像中的网格顶点,对包含在网格内的特征点使用邻近网格顶点的线性组合表示,线性组合的系数通过线性插值计算来得到,对局部配准的误差方程表示如下:
(8)
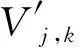
图像的全局区域需要尽可能地保留图像的自然形态,为此,应该尽可能使结果接近预拼接的近似结果。因此在全局配准阶段中设置一个二值函数Bi,其取值方法描述为:若顶点Vi附近没有特征点就设为1,否则设为0。
(9)
本文通过控制点生成最小二乘网格对图像重叠区域进行平滑处理,通过控制点和特征点进行网格调整优化,使用最小二乘网格约束计算平滑误差,如下式:
(10)
与其他的约束条件相比,最小二乘网格约束在计算过程中增加了控制点的约束条件。在网格调整过程中,图像矩阵的计算最为重要,不仅决定了图像拼接中的精度,而且影响算法的执行效率。添加控制点集信息,在计算过程中极大程度地避免了图像矩阵的无解情况,提高了图像矩阵的计算精度,虽然增加了额外的参数控制和计算开销,但是算法效率并未受到太大影响。在网格调整过程中,对拉普拉斯系数矩阵、顶点集合位置、拉普拉斯坐标矩阵和控制点集合信息的计算和使用,有效提高了图像拼接中的配准精度。
最后将配准阶段的总误差E表示如下:
E=Ep+Eg+Es
(11)
通过求解最优化方程E,完成对图像的最小二乘网格优化,得到精确的配准和拼接结果。
5 图像融合
本文使用加权泊松融合方法将配准过后的图像进行融合,传统的渐进图像融合计算简单,容易实现,但很难得到精确的融合结果,缺乏对光照变换的鲁棒性;泊松图像编辑[19]通过求解泊松方程来实现图像的无缝融合。本文将加权渐进图像融合和泊松图像融合结合起来完成图像融合。
首先使用下式进行加权渐进融合:
(12)
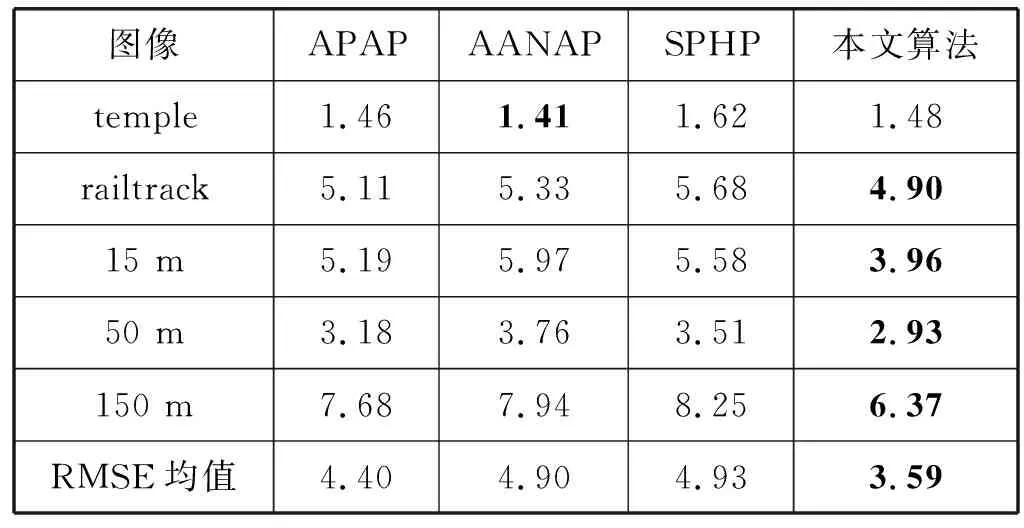
式中:w1、w2代表权值,满足w1+w2=1,0 如图4所示。泊松融合的基本思想是利用图像指导场(梯度场)对重叠区域进行插值处理,以得到重叠区域内的像素值,完成图像重叠区域的融合。 图4 泊松融合 图4中:v为原始图像中的图像块,也是需要融合的重叠区域;u为v的梯度场;S表示拼接融合后的图像,Ω表示融合图像中的重叠区域,∂Ω为重叠区域的边界。重叠区域内的像素值为f,重叠区域外的像素值为f*。图像融合过程中需要在边界处尽可能过渡平滑,降低图像边界像素值差异,因此只需要根据重叠区域Ω内的梯度值进行像素插值即可。由于融合后的图像需要保持原图像的纹理特征,像素值f可通过下式计算: (13) Δf=div(u)=div(▽v)f|∂Ω=f*|∂Ω (14) div(u)表示梯度场u的散度。通过对梯度场的散度计算以及欧拉-拉普拉斯方程,就可以得到重叠区域的像素值f,完成图像区域融合。图像融合算法的描述如算法3所示。 算法3 图像融合算法 输入:配准后的预拼接图像 输出:融合处理后的图像 1. 建入渐出法确定权值w1、w2 2. 使用式(13)进行融合处理 3. 计算全局亮度矩阵gb 4. 图像分块(10×10)以及分块亮度矩阵lb{lb1,lb2,…,lb100} 5. forifrom 1 to 100 6.db=lb[i]-gb 7. end for 8. 通过db对图像分块均匀亮度 9. 重叠区域Ω(I1/20,I1∩I2,I2/20) 10. 计算图像块v的梯度u 11. 根据式(14)-式(15)计算像素值f 图像融合算法结合了加权渐进融合算法和泊松融合算法,并在融合过程中对图像亮度进行了均匀处理,降低了图像融合过程中的亮度差异,淡化了图像拼接缝隙,提高了图像拼接效果。 本文算法使用的图像来自图像拼接相关论文数据集和无人机拍摄的图像,包括寺庙(temple)、铁轨(railtrack)以及不同高度航拍的校园图像。 首先对LIFT特征点模型与SIFT特征点模型进行比较,并使用RANSAC算法对特征点进行筛选,得到的特征点数目与特征点对匹配的准确率,比较结果如表1所示。 表1 特征点提取和准确率比较 为证明本文算法的有效性,与APAP拼接算法、AANAP算法和SPHP算法进行对比实验,结果如图5-图7所示。 (a) APAP (b) AANAP(c) SPHP (d) 本文算法图5 15 m图像拼接效果图 (a) APAP (b) AANAP(c) SPHP (d) 本文算法图6 50 m图像拼接效果图 (a) APAP (b) AANAP(c) SPHP (d) 本文算法图7 150 m图像拼接细节比较图 图5-图7分别为15 m、50 m和150 m的无人机航拍图像的拼接结果。图5的主要目标是汽车和建筑物的拼接,APAP和AANAP算法中汽车都有较为严重的重影,建筑物的轮廓和窗户的拼接有不同程度的扭曲,AANAP算法在图像边缘处产生了严重的畸变,SPHP算法放大了地面线条,本文算法较好地拼接了汽车以及建筑物目标,拼接边缘的局部调整更符合现实场景。图6的主要目标为50 m左右的房屋拼接,所有算法都很难处理房屋顶部复杂的线条,值得注意的是在路灯场景的处理中,SPHP算法取得了最好的效果,因为它最大限度地保持了非重叠区域的相似性。图7为150 m高度下操场图像的拼接,在整体图像中截取重叠区域的拼接效果比较,APAP算法拼接图像中的砖石、木棍扭曲重影都很严重,AANAP算法减弱了砖石的重影,SPHP算法中木棍拼接处痕迹较为明显,本文算法对砖石和木棍的拼接效果良好,但在砖石和木棍连接区域中的拼接效果都很模糊。从实验结果来看,本文算法的拼接效果明显优于其他拼接算法。 上述的图像拼接效果主要是从图像细节出发,对局部区域的图像拼接精度进行比较,通过图像比较的方式具有一定的主观性,常见的图像拼接质量评价参数还包括灰度标准差、熵差、交叉熵、互信息度量、结构相关性和均方误差根等。为了进一步从客观层面对拼接算法进行比较,本文使用图像均方误差根 (RMSE)对图像拼接结果进行比较。计算方法如下: (15) 式中:参数M、N代表航拍图像间重叠区域的尺寸大小;I1o(i,j)、I2o(i,j)分别代表I1、I2中拼接图像的重叠区域像素值。在计算过程中,均方误差根的值越小,说明图像的拼接融合效果越接近理想拼接结果。本文通过与其他算法比较,计算得到的RMSE值如表2所示。 表2 不同算法的RMSE值比较 由表2可知,本文算法得到的拼接图像的RMSE值在大部分情况下都取得了最优的计算结果,但在寺庙图像中,由于图像分辨率较低,视差变化较小,只需要进行简单的图像变换就能得到精确的拼接结果,因此得到的计算结果稍差于其他算法。通过RMSE值的计算比较进一步证明了本文算法的优越性。 本文算法和比较算法中图像网格大小都选取10×10,统计本文拼接算法和其他拼接算法的运行时间,结果如图8所示。 图8 算法运行时间比较图 由图8可知本文算法的耗时较短,LIFT特征点的检测和匹配过程更加快速,有效弥补了算法在进行控制点生成过程中的消耗。在整个图像网格的调整过程中,运算时间受到图像重叠区域面积的影响,重叠区域越大,特征点检测和网格调整消耗的时间就越长。 本文通过使用LIFT模型获取了图像特征点信息,对特征点进行筛选得到控制点,使用控制点和特征点生成网格,利用最小二乘网格约束对图像网格进行优化,从而得到了更好的图像配准效果,再利用优化的加权泊松图像融合得到图像拼接结果,并通过实验验证了算法的有效性,提高了航拍图像的拼接精度。但是由于航拍图像内容十分丰富,局部的细节很难得到有效的处理,尤其是图像内容复杂和图像场景重合连接的区域,重影的现象依然局部存在,而且航拍图像的数据量很大,算法的执行效率很难提高,算法依然存在较大的优化空间。
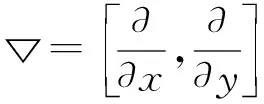
6 实 验





7 结 语

