基于遗传算法的集成电路板下料算法

阚海明 胡晓彦

摘要：为了解决集成电路板（PCB）在生产过程中的自动排布问题，实现不同类型PCB板的一次性自动套裁排样，在传统自适应遗传算法基础上引入了梯度概念，实现了适用于PCB的自动排样算法（AGA_Grad）。相比现有成熟的PCB板套裁排样软件，AGA_Grad有参数设置简单、计算收敛速度更快及排列更优等优点，用于指导工业生产，能够明显提高多种类型PCB板的排样速度。

关键词：矩形排样；电路板下料；动态规划；遗传算法

中图分类号：TP18文献标志码：A文章编号：1008-1739（2020）07-58-3

0引言

矩形排样已有比较成熟的算法，算法时间和排样结果基本都能满足生产需要。但在一些小批量、多品种的集成电路下料生产过程中，经常会面临将多种类型、大小不一PCB放在同一个工作板上布局的问题，该问题属于典型的套裁排样，不仅需要考虑板材的布局，还要考虑待加工PCB的自身形状。当前该类算法大致分为3类：①以传统精确算法实现排样，但耗时较长；②生成普通排样的近似算法；③根据自身特性及生产情况，一定程度上进行简化。文献[1-4]提出生成最优2段排样方式的确定型算法，一定程度上简化了切割过程；文献[5]中的动态规划算法解决了考虑切割刀数的2段排样方式，对工业生产有一定的指导作用；文献[6-8]在传统单一排样算法、套裁排样算法基础上进行了改进。

企业PCB生产过程有小批量、多品种的典型特点，需要实现套裁排样加工，本文将遗传算法应用在其中实现了PCB套裁排样，得到了理想效果。

1问题描述

1.1 PCB下料问题

在实际生产过程中，需要将不同类型的PCB尽可能多地拼放在同一张母板上，经过工艺成型将定型的PCB单元板再切割下来，从而达到一次性生产多个PCB的目的，这样有助于在一定程度上简化下料过程。

PCB下料过程中可将单张板材切割成若干大小尺寸不等和价值已知的矩形毛坯，约束条件有：①确定工作板尺寸；②毛坯数量不确定，毛坯位置不能重叠，毛坯之间距离可调整；③使得板材中排入的毛坯数量尽可能多，整体材料利用率最大，整体材料利用率计算公式为：材料利用率=（毛坯数量*单个毛坯面积/板材总面积）*100%。

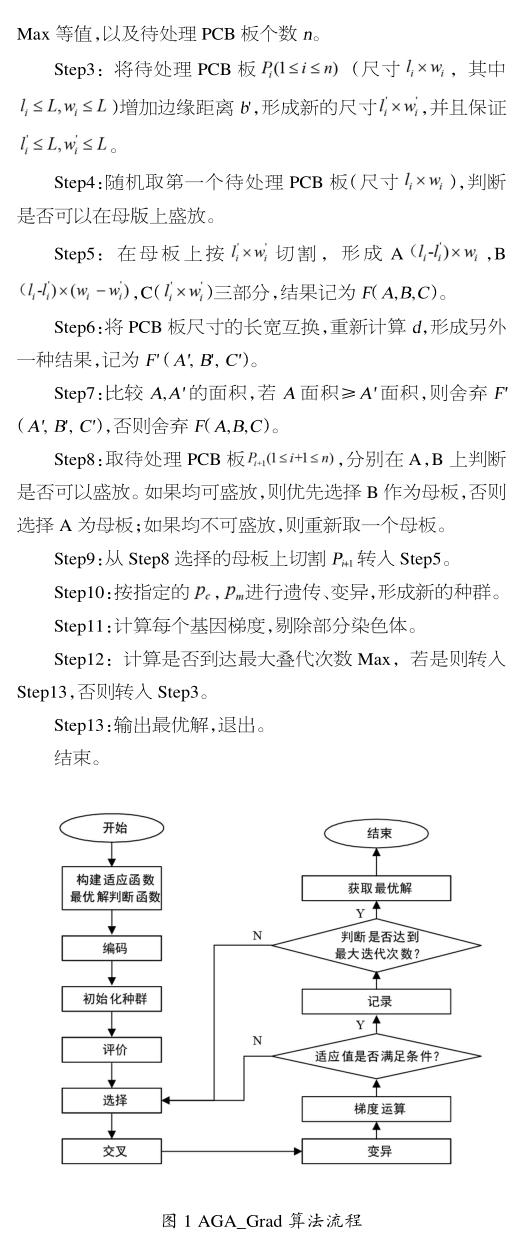
3实验结果分析

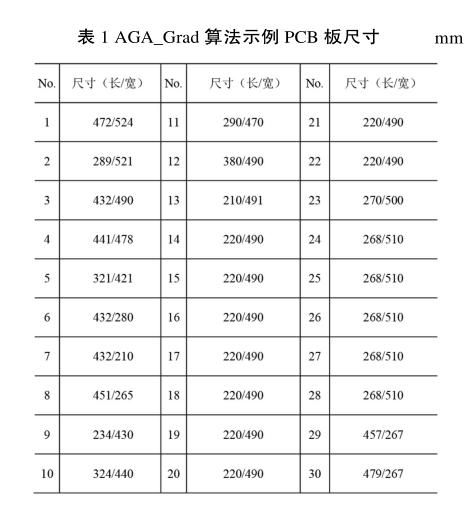
为了测试AGA_Grad算法的合理性，做了测试，随机生成30组PCB板尺寸，选择母板为2 500mm*3 000mm，如表1所示。

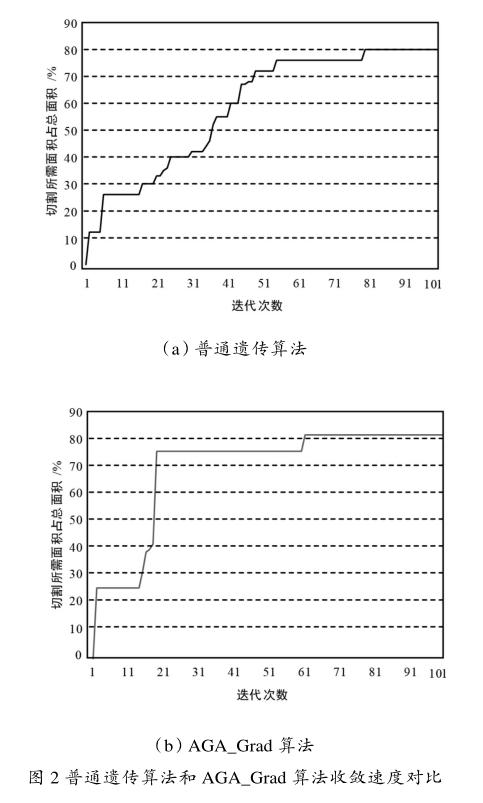
为了方便比较，分别采用普通遗传算法和AGA_Grad算法对表2中PCB板进行切割排序，实际计算时发现二者所需时间相差无几，但收敛速度AGA_Grad算法明显优于普通遗传算法，迭代次数对比如图2所示。

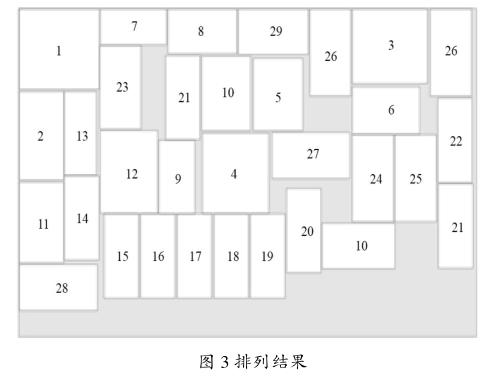
PCB板的排列结果如图3所示，其中切割使用面积占总面积的82%。

4結束语

本文研究了PCB板实际生产过程中的排样问题，在自适应遗传算法的基础上引进了梯度概念，提出了AGA_Grad算法，并结合某研究所实际生产数据证明了该算法的有效性，获得了满意的效果。

参考文献

[1] CUI Yaodong，HE Dongli，SONG Xiaoxia.Generating Optimal Two-section Cutting Patterns for Rectangular Blanks[J]. Computers & Operations Research，2006，33（6）：1505-1520.

[2] CUI Yaodong.A New Dynamic Programming Procedure for Three-staged Cutting Patterns[J].Journal of Global Optimization， 2013， 55（2）：349-357.

[3]季君，陆一平.查建中，等.生成矩形毛坯最优两段排样方式的确定型算法[J].计算机学报，2012，35（1）：183-191.

[4]孔令熠，陈秋莲.二维多阶段矩形剪切排样算法[J].计算机应用与软件，2015，32（5）：231-233.

[5]罗丹，崔耀东，李秋蓉.生成匀质块排样方式的递推算法[J].计算机工程与设计，2013，34（3）：1112-1115.

[6]潘卫平，陈秋莲，崔耀东.考虑切割刀数的最优两段排样算法研究[J].广西大学学报（自然科学版），2014，39（3）：687-692.

[7]李东兴.同尺寸集成电路板下料算法研究[D].南宁：广西大学，2016.

[8] FAYARD D，ZISSIMOPOULOS V. Approximation Algorithm for Solving Unconstrained Two-dimensional Knapsack Problems[J]. European Journal of Operational Research， 1995，84（3）：618.