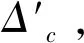F-P腔内自旋轨道耦合玻色-爱因斯坦凝聚体的色散研究

姚珩煜，杨 波，刘子龙，张 波

(武汉理工大学理学院物理系，武汉 430070)

1 引 言

自1995年，科学家基于激光冷却的技术在实验上实现了玻色和爱因斯坦预言的玻色-爱因斯坦凝聚体(BEC)起[1-3]，冷原子系统为模拟物质在超低温情况下的量子效应和研究光与物质相互作用提供了一个理想的纯净平台[4,5].在光学微腔与超冷原子的组合系统中，腔场的光学模式和原子的自由度相耦合，产生了周期性的依赖于原子密度和腔中位置的量子化光晶格，出现了丰富的物理性质[6-9].此时，通过腔参数的调节，能有效地改变光晶格的阱深，冷原子的运动就类似于固体理论中布洛赫电子的运动，就能有效地在BEC中实现扩展Bose-Hubbard模型[10,11].而且，由于腔损耗的存在，使系统能处于动力学稳态，也为非破坏性测量提供了的可能性.另一方面，2005年非阿贝尔人工规范场理论[12,13]的出现为中性超冷原子系统中自旋轨道耦合(SOC)的实现提供了理论解决方案.而此后，大多数在超冷原子系统中产生SOC的实验[14-19]是通过用一对Raman激光作用于中性冷原子的两个不同赝自旋态[20,21]，引入具有空间依赖的光学耦合来实现一个维度上的SOC.近年来在光学微腔与超冷原子的组合系统中考虑SOC的情况开始在理论上被讨论，为研究非平庸拓扑物相[22-24]提供了很好的平台.本文考虑在外加经典激光相干驱动的单模Fabry-Pérot(F-P)腔内的BEC上引入SOC作用，SOC为冷原子系统提供了一个人工规范势，光学腔则提供了周期性的量子化光晶格，使用紧束缚近似进行二次量子化，在合适的腔参数调节下得到了单原子缀饰态能级的具体表达式，讨论了外加Raman光和磁场对原子色散的影响，证明在BEC中产生了可调节的一维狄拉克点.

2 理论模型

考虑一个光轴沿x方向的单模F-P腔，腔模g0cos(Kx)，腔光场固有频率为ωc，耗散为κ，并沿腔轴的方向加入一个频率为ωp，泵浦率为η的经典强泵浦场，即腔驱动场.考虑N0个处于|F=1,mF=-1〉态87Rb原子制备的BEC放置于F-P腔内，在外加沿z方向的磁场作用下，由于二次型Zeeman劈裂较大，超精细能级中的|F=1,mF=1〉态被有效地抑制.当沿x轴成45°射入两束弱的频率分别为ωL和ωL+ΔωL相互垂直的Raman光作用于|F=1,mF=0〉和|F=1,mF=-1〉两个磁子能级和一个激发态|e〉时，能形成有效的Rashba型和Dresselhaus型等权叠加的SOC[14,15].SOC作用于冷原子提供一个x方向人工规范势，人工合成了赝自旋为1/2的BEC，两个磁子能级就相当于赝自旋态|↑〉和|↓〉，如图1所示.此时，用偶极近似和旋波近似可以给出单原子的哈密顿量(取自然单位ħ=1)

图1 模型及能级示意图Fig.1 Model and energy levels diagram

(1)

(2)

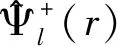
(3)

由方程(2)利用海森堡运动方程可得到光子算符和处于不同能级的原子算符的动力学演化过程

(4)

其中，σ=↑,↓代表原子的两个赝自旋态.当原子跃迁频率与泵浦光的失谐量远大于原子线宽γ，即Δa≫γ时，进行绝热近似，取∂tΨe(r)=0得到

(5)

将方程(5)代入(4)，则消除激发态可以改写系统的哈密顿量为

(6)

W(r-ri)=e-imφijω(r-ri)

(7)

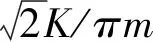
(8)

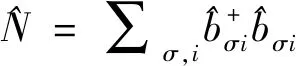
(9)

(10)

(11)

图2 三个高阶项系数随有效失谐量的变化Fig.2 Variation of the three high-order terms' coefficients with the effective detuning

(12)

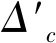
(13)

利用欧拉公式就可以得到单原子的哈密顿量

(14)

将方程(14)对角化，得到缀饰态能级的表达式为

(15)

3 结果与讨论

图3 原子色散随单Raman光子反冲动量的变化Fig.3 Variation of the atom's dispersion with the recoil momentum of single Raman photon

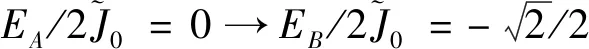
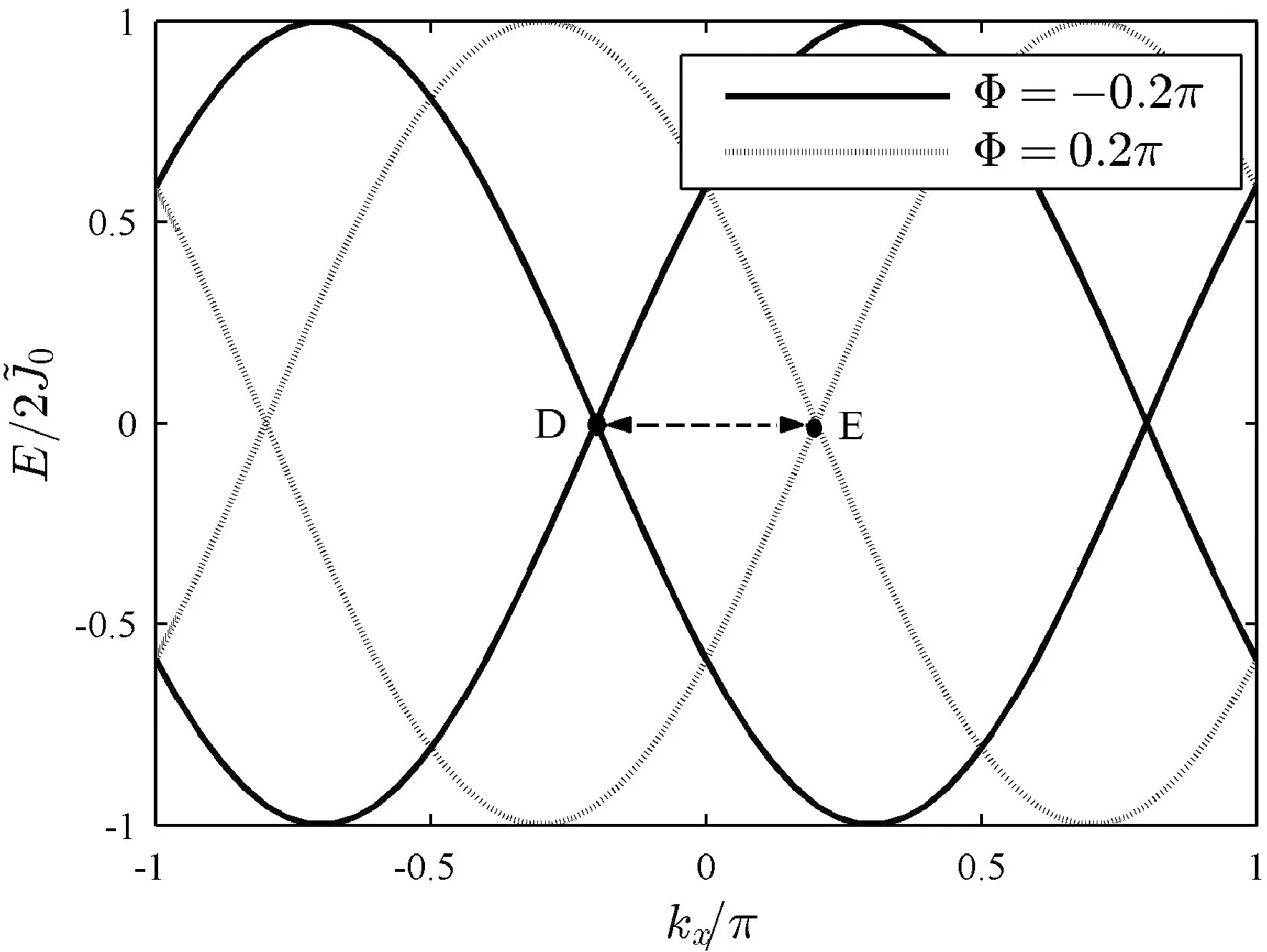
图4 原子色散随Zeeman磁场的变化Fig.4 Variation of the atom's dispersion with the Zeeman magnetic field

4 结 论