高温高压下碳化钨晶体的结构、力学、电子、光学以及热力学性能的第一性原理计算

易怀星,王臣菊,孙 斌,顾建兵

(中原工学院 材料与化工学院，郑州 451191)

1 引 言

过渡金属碳化钨是一种性能非常优良的材料.它有极高的硬度、耐磨性，并且碳化钨与熔融金属之间拥有良好的润湿性，可用于制造磨损领域的胶结元件[1].碳化钨还表现了优良的热稳定性和化学稳定性，在催化工业中具有重要的应用价值，是贵金属的良好替代品[2].碳化钨也是一种超导材料[3].此外，碳化钨及其硬质合金用于切削工具或耐磨材料，是高压实验和技术中的重要组成部分，这意味着碳化钨有着巨大的工业应用价值和广泛的应用前景.

2008年，Zhang等人利用第一性原理对碳化钨的相结构、电子结构、力学性能和化学键合性能进行了系统的理论研究[4].2009年，Lin等人采用第一性原理平面波超软赝势的方法，证实了碳化钨各向异性压缩系数和较低体积模量的实验观测结果[5].Kavitha研究了碳化钨的超导性能，包括碳化钨相(WC)、闪锌矿相(ZB)，纤锌矿相(WZ)的碳化钨，探讨了碳化钨的超导转变温度和结构相变压强[6].Zhukov和Gubanov证实了碳化钨的体积模量(655 GPa)和德拜温度(648 K)非常高，这在一定程度上解释了碳化钨作为切削材料的原因[7].终上所述，关于碳化钨的能带结构和弹性常数计算较多，但光学性质和热力学性质的研究报道较少.但是碳化钨常被用于高温高压的工作环境下，研究热力学性质对确定碳化钨在高压和高温下的特殊性能具有重要的意义.

因此本文采用密度泛函理论，研究了碳化钨的电子结构、弹性常数、光学和高温高压下的热力学性质.在第二部分，我们简要地描述了计算方法；第三部分中给出了计算结果，与已有的实验数据和理论结果进行了比较并讨论；在第四部分中给出了结论.

2 计算方法

2.1 总能计算

在密度泛函理论的框架下[8,9]，使用CASTEP模块[10]计算了碳化钨的力学性质、电子性质、光学性质和热力学性质.利用广义梯度近似中的Perdew-Burke-Ernzerhof方法计算了Kohn-Shan方程[11].利用超软赝势描述了价电子与离子核之间的相互作用.W和C的价电子分别为5d46s2、2s22p2.如图1所示，WC相碳化钨结构的坐标是W(0,0,0)，C(0.667,0.333,0.5).ZB相碳化钨的坐标是W(0,0,0)，C(0.25,0.25,0.25).WZ相碳化钨结构的坐标是W(0.5,0.667,0)，C(0.333,0.667,0.375).WC，ZB，WZ结构的空间群分别为P6M2(187)、F43m(216)和P63mc(186).对于WC，ZB和WZ相碳化钨，经过收敛性测试，所选平面波截断能分别为550 eV，650 eV和650 eV，布里渊区K点分别取15×15×13，14×14×14和14×14×7.系统优化的能量收敛值设为5×10-6eV/atom，对原子的最大作用力小于0.001 eV/A.采用Broyden-Fletcher-Goldfarb-Shenno (BFGS)算法优化这些结构的平衡晶体参数和原子位置.计算声子谱时的赝势为模守恒赝势，并使用有限位移法计算碳化钨声子色散关系[12,13].

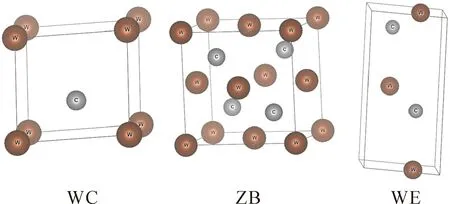
图1 碳化钨三种相的晶体结构图Fig.1 Crystal structure diagrams of three phases of tungsten carbide.

2.2 弹性性能

本文用应力-应变方法σij=Cijkl.εkl对碳化钨的弹性常数进行计算[14]，其中σij是应力张量，εkl是应变张量，Cijkl是弹性常数张量.体积模量(B)、杨氏模量(E)、剪切模量(G)和泊松比(υ)可以通过Voigt-Reuss-Hill (VRH)近似来计算[15].对于六方结构的晶体，B和G的计算方程如下[16]

(1)

(2)

其中：

(3)

(4)

(5)

(6)

其中：

(7)

杨氏模量E、泊松比υ则可由下面公式推导出[17]：

(8)

(9)

2.3 热力学性质

本文在温度0～3000 K，压力0～300 GPa的条件下，应用简谐波德拜模型[18,19]计算了碳化钨的热力学性质，包括体积比V/V0、热容CV、德拜温度ΘD、热膨胀系数α和格林艾森系数γ，其中非平衡条件下的吉布斯函数G*(V,p,T)可表示为：

G*(V,p,T)=E(V)+pV+A[ΘD(V),T]，

(10)

式中E(V)为每个单胞的总能量，pV为恒静压条件，ΘD为德拜温度，A为亥姆霍兹自由能，可以表示为[20]：

(11)

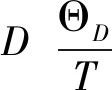
德拜温度ΘD可由下列式子计算[21-23]：

(12)

(13)

(14)

(15)

这里h是普朗克常数，NA是阿伏伽德罗常数，ρ为理论密度，M是单位晶胞的分子量，νm为平均声速，νt为横向声速，νl为纵向声速.则关于体积V的非平衡吉布斯函数G*(V,p,T)可以表示为：

(16)

求解方程(16)，我们可以得到热状态方程.等温体积弹性模量BT、热容CV和热膨胀系数α计算方程式为[24]：

(17)

(18)

(19)

其中格林艾森系数γ表达式为：

(20)

2.4 光学性质

碳化钨的光学性质可以通过光学参数来分析，即复介电函数、吸收系数、反射率、折射率、光电导率和能量损失谱.复介电函数表示为[25]：

ε(ω)=ε1(ω)+iε2(ω)，

(21)

其中：

ε1(ω)=n2-κ2，

(22)

ε2(ω)=2nκ，

(23)

式子中n为折射率，κ为消光系数.下面的公式表示虚部ε2(ω)[25]：

(24)

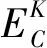
(25)

根据复介电函数、吸收系数、消光系数、折射率和电子能量损失谱的关系，吸收系数α(ω)、反射率R(ω)、能量损失率L(ω)和光电导率σ(ω)可由下列公式给出[25,26]：

(26)

(27)

(28)

(29)

3 结果与讨论

3.1 结构性质

表1 平衡状态下三种相的碳化钨晶体的计算参数与现有理论值和实验值的比较
Table 1 Comparison of calculated parameters with existing theoretical and experimental values of three phases of WC under equilibrium state.

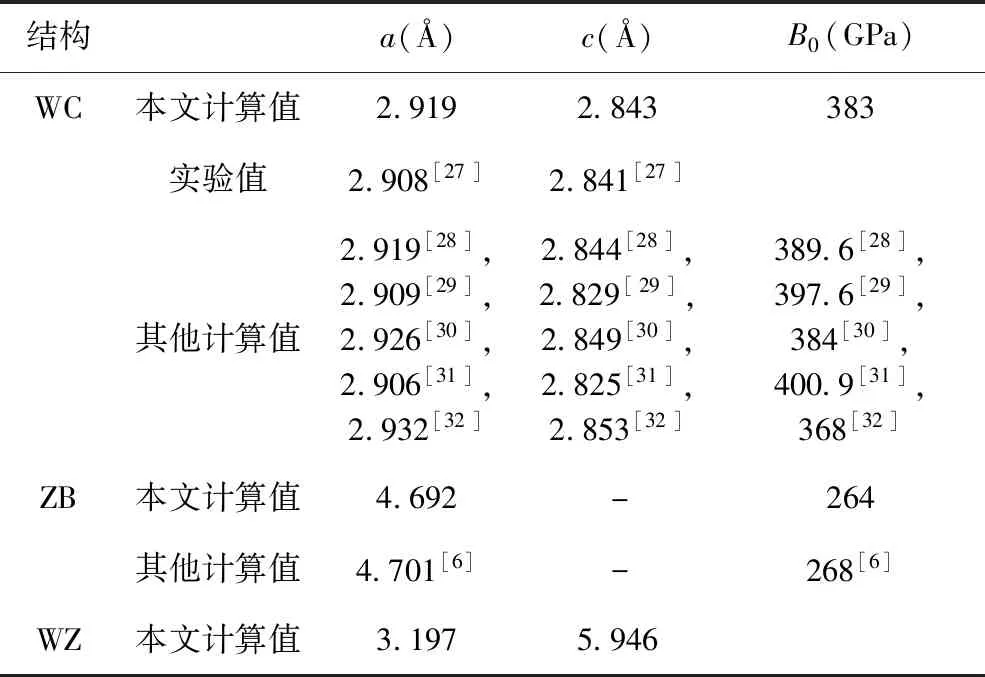
结构a(Å)c(Å)B0(GPa)WC本文计算值2.9192.843383实验值2.908[27]2.841[27]其他计算值2.919[28],2.909[29],2.926[30],2.906[31],2.932[32]2.844[28],2.829[29],2.849[30],2.825[31],2.853[32]389.6[28],397.6[29],384[30],400.9[31],368[32]ZB本文计算值4.692-264其他计算值4.701[6]-268[6]WZ本文计算值3.1975.946

为了保证计算的可靠性，首先对晶体结构进行优化，然后得到0 K下的晶格参数，如表1所示.我们的结果与前人的计算数据误差小于5%，证明了本研究使用的参数是可靠的.

化合物的热力学稳定性与生成焓有关，当化合物的生成焓为负时，该化合物是稳定的.生成焓值越小，化合物越稳定.本文计算了碳化钨晶体的三种结构(WC，ZB，WZ)在压强下的生成焓，如图2所示.

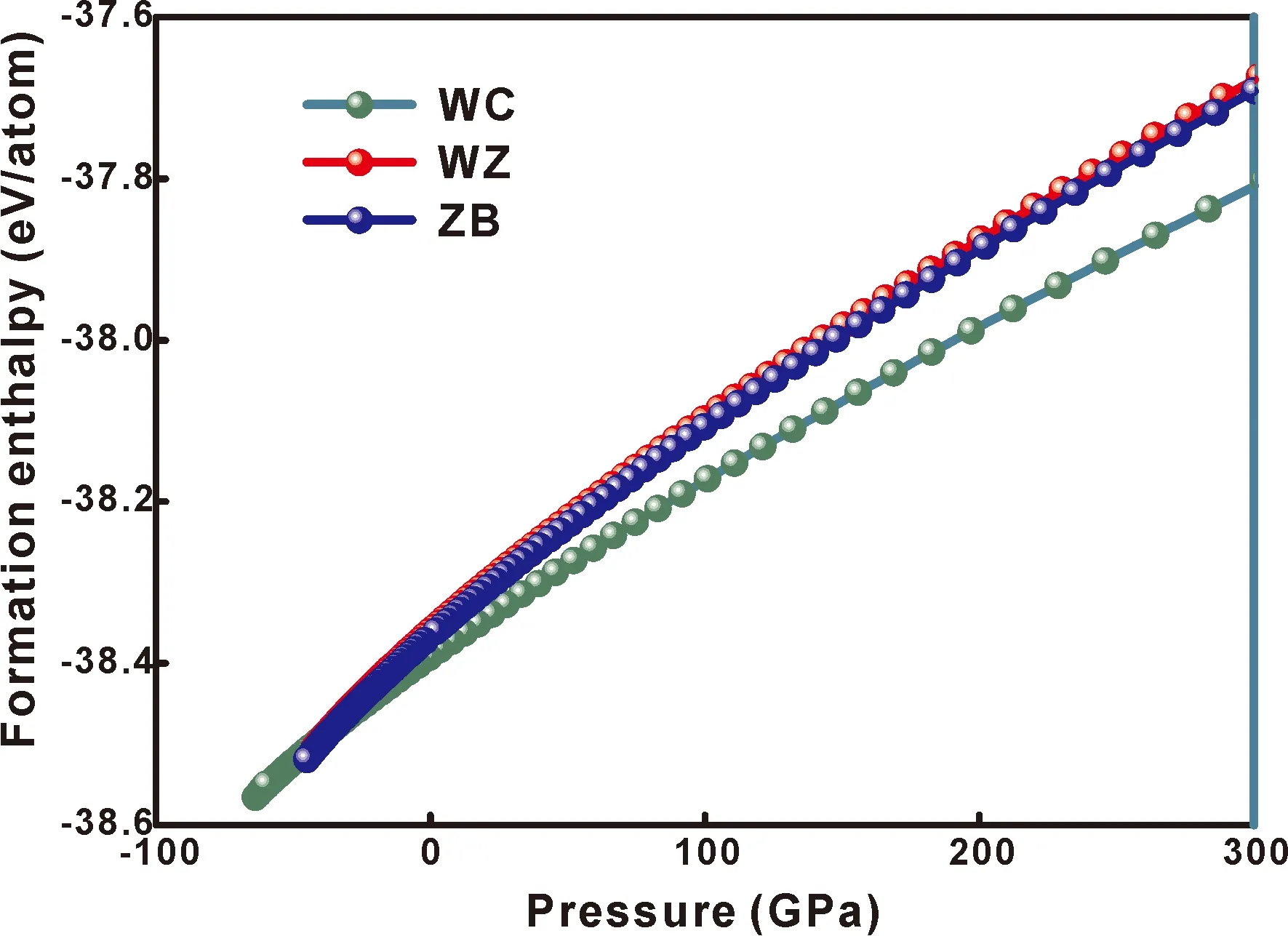
图2 碳化钨晶体三种相的生成焓随压力的变化曲线Fig.2 The change curves of formation enthalpy of WC with three phases under pressure.

如图2所示，WC结构在整个压力范围内具有最低的生成焓，是最稳定的结构.为了进一步研究它们的热力学稳定性，本文计算了一系列的E-V数据，并将其展示在图3中.从图中可以看出WC结构的碳化钨最稳定.从总能量和体积的曲线上也可以看出一阶相变.相变压力Pt是公切线的梯度，可以表示为[33]：

(30)

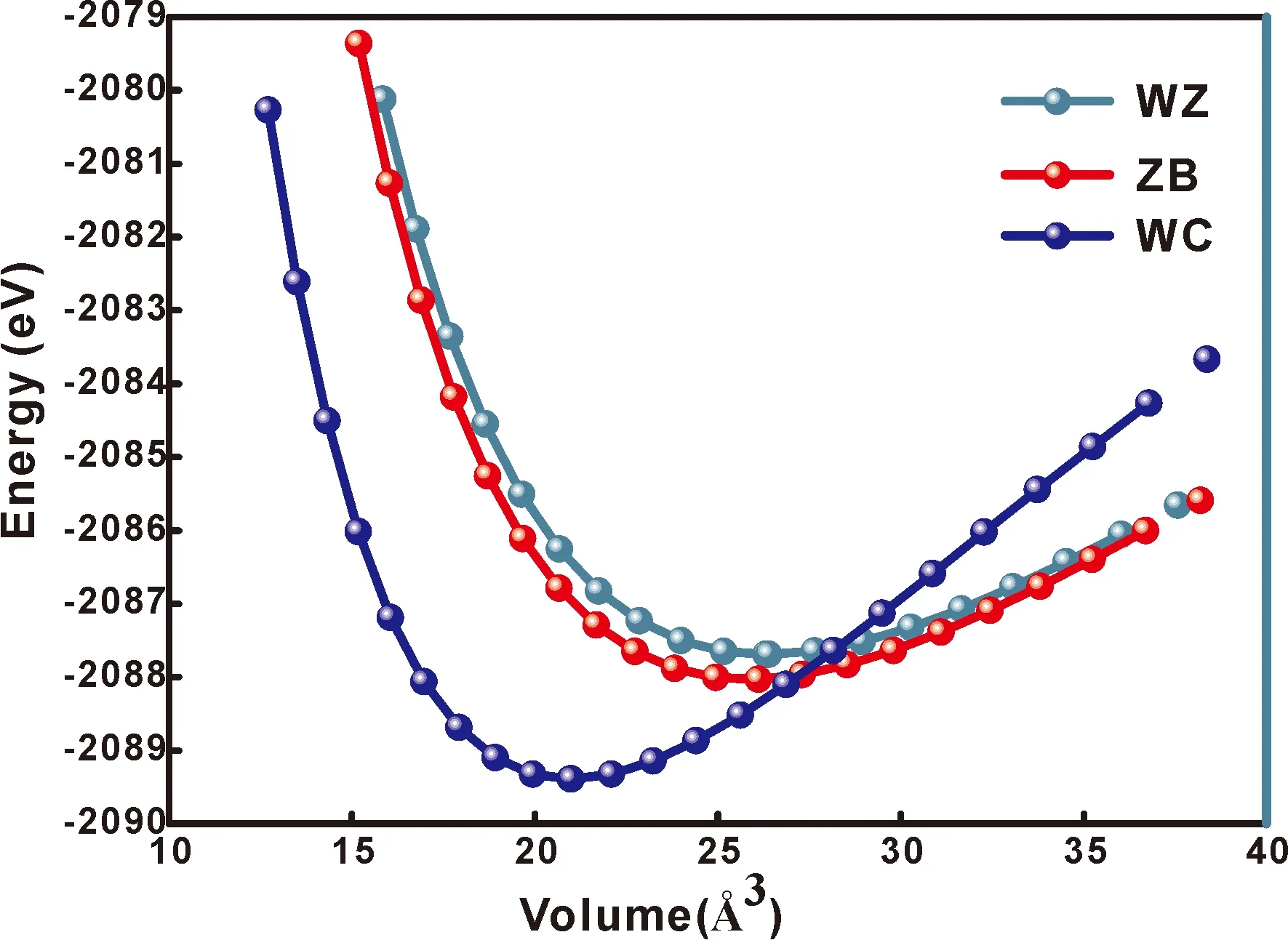
图3 0 GPa和0 K下碳化钨三种相的总能量与晶胞体积的变化关系Fig.3 Relationships between total energy and cell volume for three phases of WC at 0 GPa and 0 K.

从图中可以清楚的看出，三种结构的碳化钨的总能量都随着其体积的增加，呈现出先降低后增加的趋势.并且WC结构的稳定性最好.因此，下文我们只讨论WC结构碳化钨的性质.

3.2 力学性质

表2总结了我们的关于力学性质的计算结果，并与现有理论值和实验值进行了比较.使用Born-Huang稳定性判据可以判断化合物的力学稳定性，对于六方结构，其力学稳定性判据为[34]：

C12>0，C33>0，C66=(C11-C12)>0，C44>0，

(31)

参照方程(31)，发现WC相碳化钨符合机械稳定性的标准.

体积模量是反映材料抗体积变化的能力，表征材料抗变形能力的参数.一般来说，体积模量越大，化合物的硬度越高[35].WC的体积模量很大，这意味着碳化钨具有很高的硬度.碳化钨的剪切模量(280.4 GPa)和杨氏模量(677.2 GPa)很高，表明WC具有相当大的抗弹性变形能力.体积模量与剪切模量之比(B/G)可以用来判断化合物是脆性还是韧性.当B/G值大于1.75时，该化合物是延展性的，否则该化合物是脆性的[36].如表2所示，WC的B/G值小于1.75，因此它是脆性的.泊松比也可以用来表征材料的脆性或延展性.当泊松比大于(小于)0.26时，化合物表现出延展性(脆性)[37].如表2所示，碳化钨的泊松比小于0.26，表明了它是脆性材料.

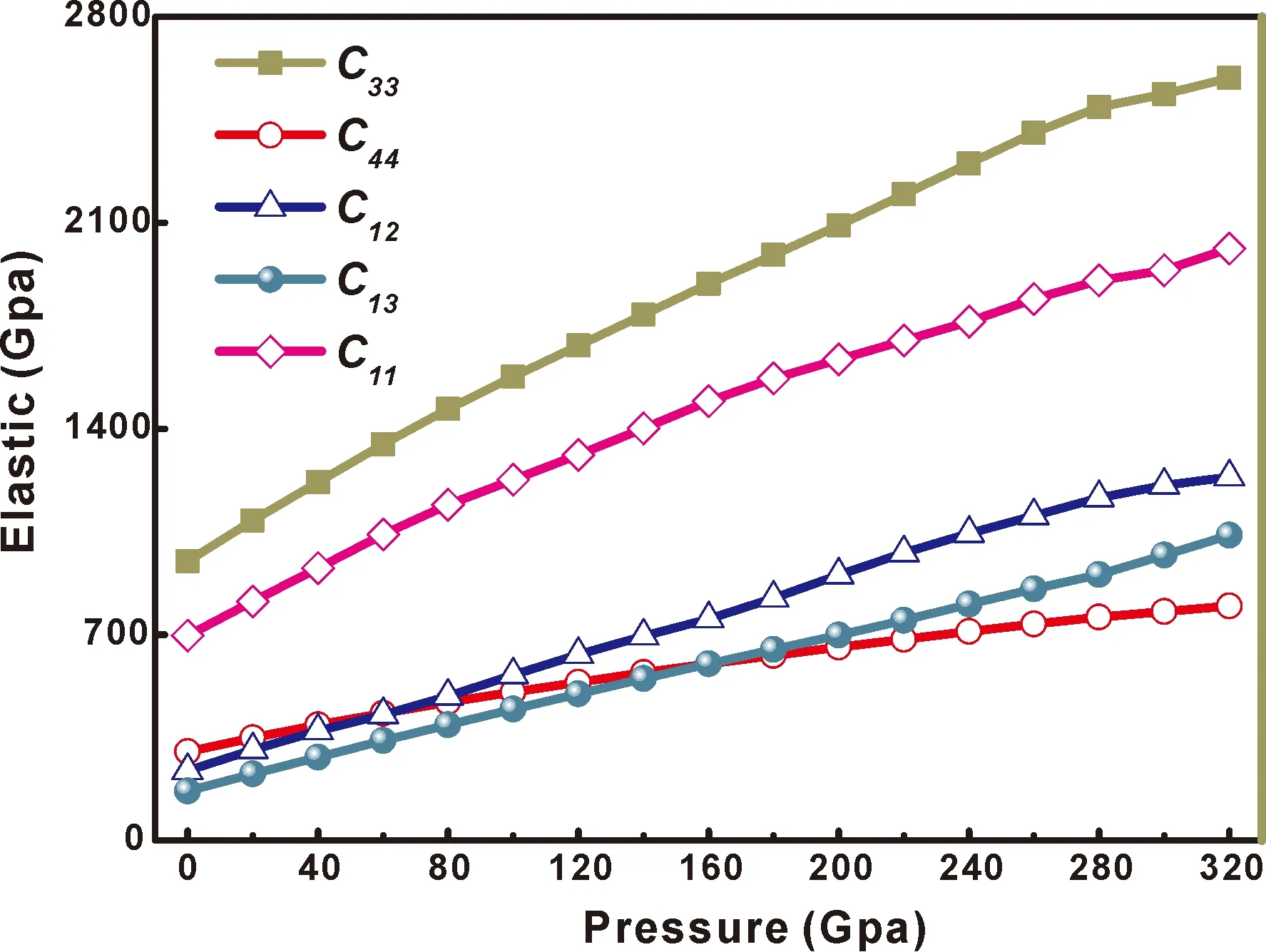
图4 0 K时，压强对WC弹性常数的影响Fig.4 Effect of pressure on the elastic constants of WC at 0 K.

为了探究WC在高压下的压缩性，我们计算了WC的弹性常数随压强的变化关系.如图4所示，碳化钨的弹性常数Cij随着压力P的增加而增大，这意味着碳化钨的可压缩性变得越来越困难.

3.3 电子性质

本文计算得到了在零温零压下WC沿布里渊区高对称点方向的能带结构.如图5所示，选取了0 eV为费米能级，并选取了费米能级附近-25 eV到25 eV的能带结构.从图中可以观察到，WC的能带分散在整个布里渊区域，有一部分穿过费米能级，证实了WC的金属性.

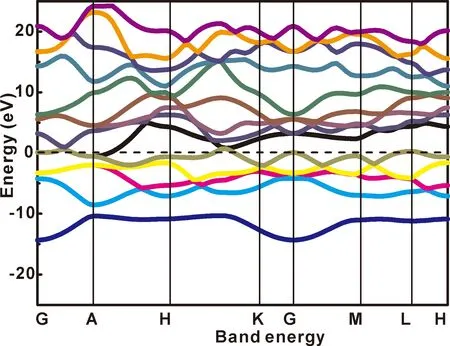
图5 0 GPa和0 K下WC的能带结构Fig.5 Band structures for WC at 0 GPa and 0 K.

图6显示了WC的总态密度(TDOS)和部分电子态密度(PDOS)，WC的态密度穿过费米能级，符合金属性的特征，和上文能带结构得到的结论一致，这再次证明了WC的金属性质.WC的电子结构主要由C-p带和W-d带决定.此外，费米能级也由W-d带和少量C-p带决定，而且计算的态密度值在费米能级附近具有最小值，这反映了2p轨道和5d轨道杂化所产生的成键和断键.

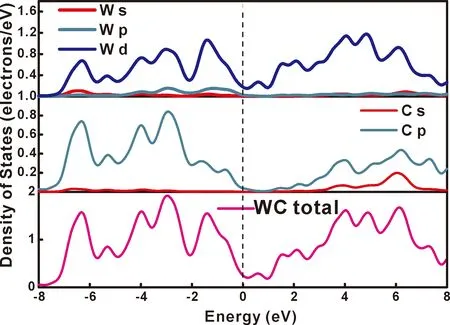
图6 0 GPa和0 K下WC的态密度Fig.6 Density of states for WC at 0 GPa and 0 K.

3.4 声子谱

判断固体相是否稳定，依据之一便是动力学稳定性.即声子谱在任意点均不出现虚频，某一支声子谱软化表示动力学稳定性减弱[39].为了检验WC的动力学稳定性，我们使用有限位移法计算了0 GPa和300 GPa下的声子谱与声子态密度曲线.计算结果如图7和8所示.由图7(a)和8(a)可知，在0 GPa和300 GPa压强下，WC晶体结构的声子色散在整个布里渊区没有虚频，说明该结构是动态稳定的.声子态密度曲线如图7(b)和8(b)所示，0 GPa和300 GPa压强下分别在频率6 THz和31 THz处存在一个最大的峰值，表明WC晶体的晶格振动比较集中在该频率附近.

图7 0 K和0 GPa下，WC的声子谱 (a) 和声子色散 (b)Fig.7 Phonon spectrum (a) and density of phonon states (b) of WC at 0 K and 0 GPa.

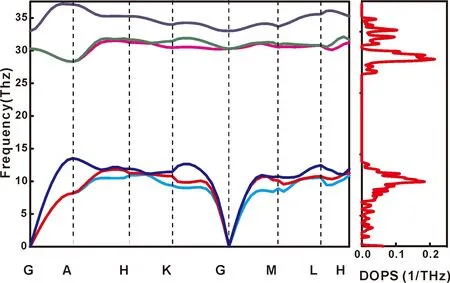
图8 0 K和300 GPa下，WC的声子谱 (a) 和声子色散 (b)Fig.8 Phonon spectrum (a) and density of phonon states (b) of WC at 0 K and 300 GPa.

3.5 热力学性质

研究热力学性质对确定这些材料在高温高压下的特殊性能具有重要的意义，包括体积比V/V0、热容CV、德拜温度ΘD、热膨胀系数α和格林艾森γ.

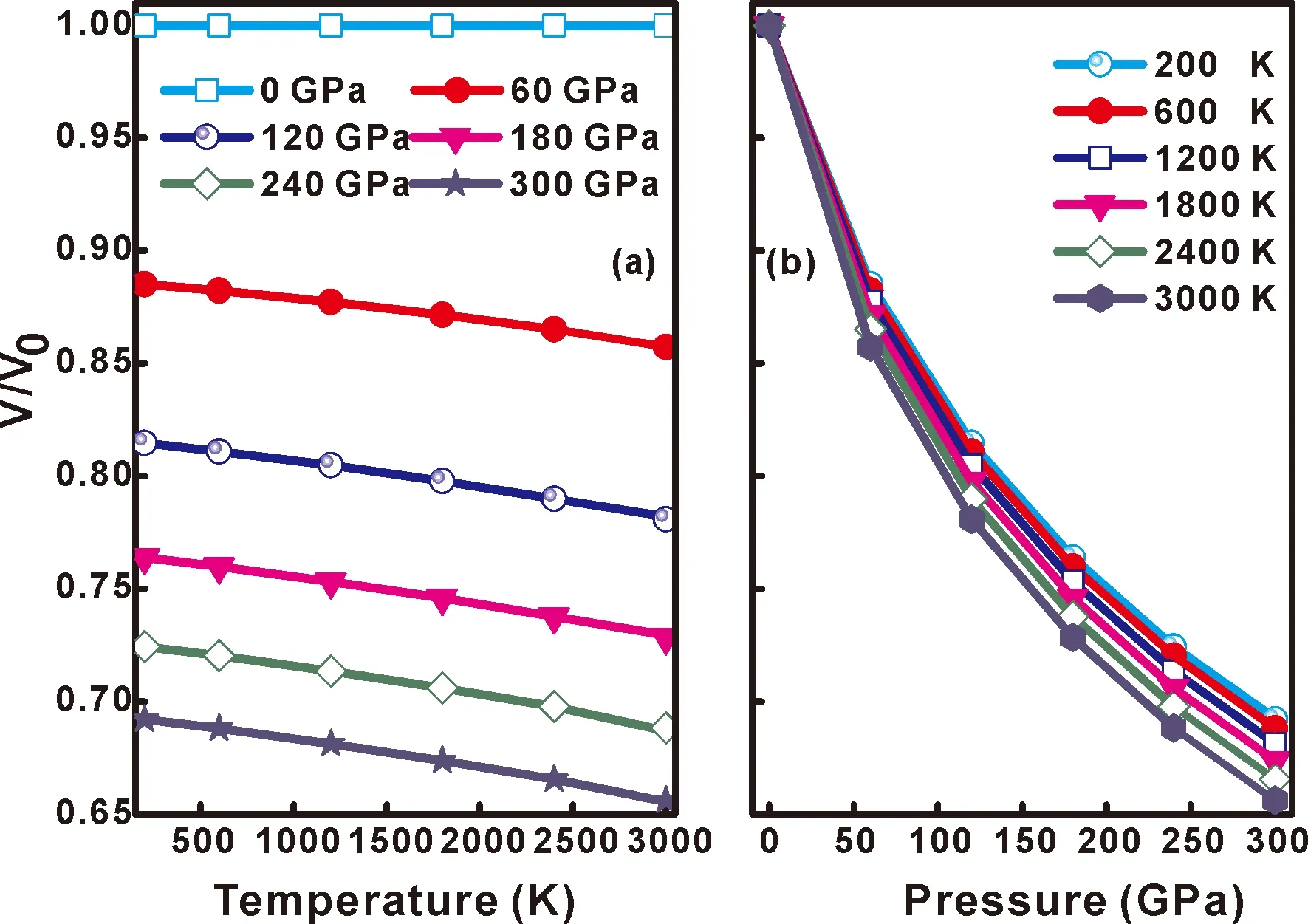
图9 温度 (a) 和压强 (b) 对WC的V/V0的影响Fig.9 V/V0 versus temperature (a) and pressure (b) for the WC.

体积比V/V0随压强和温度的变化情况如图9所示，其中V是WC原胞在一定压强下的体积值，V0是零压下平衡态的原胞体积.从图9(a)中可以看出，压强一定时，随着温度的升高，V/V0逐渐减小，但是变化幅度不大，并且0 GPa下的V/V0不随温度变化而变化.从图9(b)可知，在给定温度下，体积比V/V0随着压强的增大而减小，在相同压强下，低温条件下的V/V0要大于高温条件下的.总而言之，V/V0对压强的变化更敏感.

图10(a)和10(b)分别描述了热容CV随压强和温度的变化情况，由图10(b)可以看出，在压强一定，温度小于800 K时，热容随温度的升高而增大，并且增加很迅速.当继续升高温度时，热容CV增长缓慢，这表明WC中离子之间的相互作用对低温下的热容有很大的影响.在高温下，CV曲线近似一条直线，说明热容CV接近Dulong-Petit极限.当温度小于600 K时，温度对热容的影响要大于压强对热容的影响.

图10 压强 (a) 和温度 (b) 对WC的热容CV的影响Fig.10 The heat capacity CV versus pressure (a) and temperature (b) for the WC.

无论是理论方面还是实验方面，热膨胀系数α对于预测体系的热力学状态方程都具有重要的意义.图11(a)和11(b)表示了WC的热膨胀系数α随压强和温度的变化关系.从图11(a)可以看出，对于WC，在一定温度下，热膨胀系数α在低压下急剧下降，随着压强增大逐渐趋于平缓.从图11(b)可以看出，热膨胀系数α随着温度的增加而增加，并且给定压强下热膨胀系数α在600 K温度以上增长非常缓慢.最后值得一提的是，热膨胀系数α的值在零压下要比在其他压力下的值大得多.

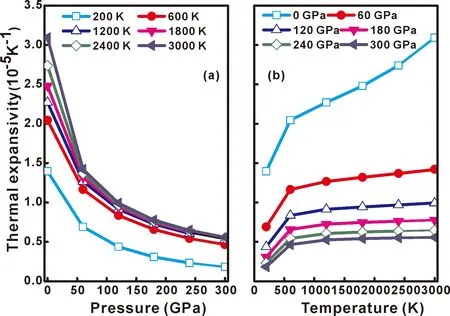
图11 WC的热膨胀系数α与压力 (a) 和温度 (b) 的关系Fig.11 The thermodynamic expansivity α versus pressure (a) and temperature (b) for the WC.

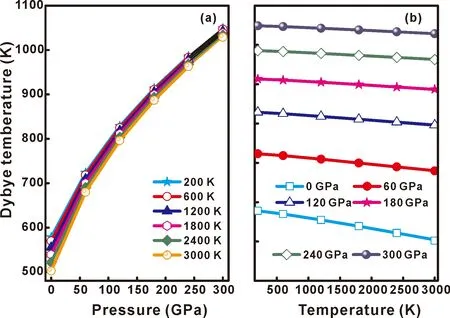
图12 WC的徳拜温度ΘD与压力 (a) 和温度 (b) 的关系Fig.12 The Debye temperature ΘD versus pressure (a) and temperature (b) for the WC.

德拜温度ΘD随温度和压强的变化关系如图12(a)和(b)所示.图12(a)给出了不同温度下碳化钨的ΘD与压强的变化关系.结果表明，温度一定时，德拜温度ΘD随着压强的增加而增加.图(b)给出了不同压强下碳化钨的ΘD与温度的变化关系.由图12(b)可以看出，在压强一定时，德拜温度ΘD随温度的升高而呈现减小的趋势.并且我们还发现，德拜温度ΘD受温度的影响远小于受压强的影响.

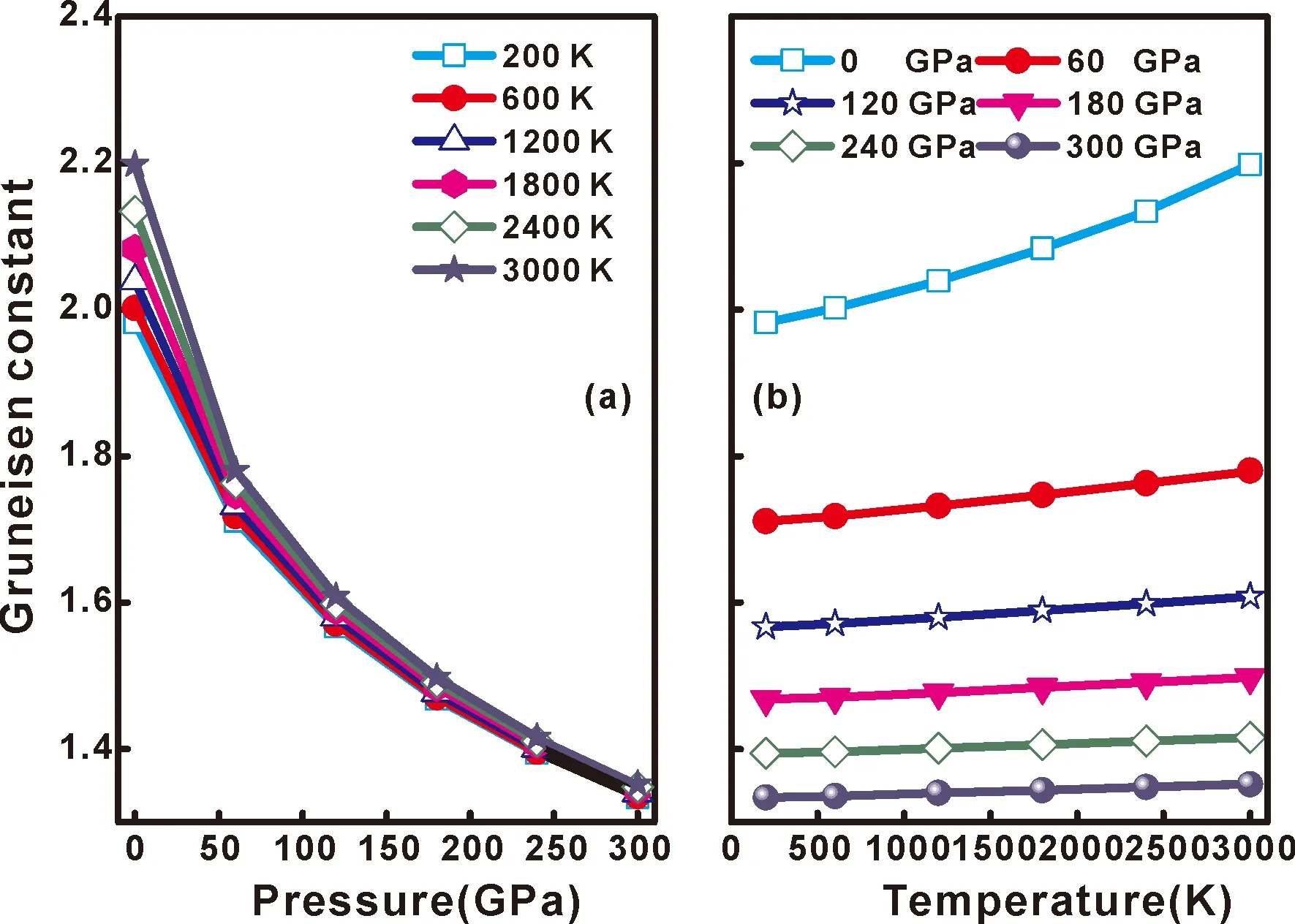
图13 WC的格林艾森系数 γ 与压力 (a) 和温度 (b) 的关系Fig.13 The Grüneisen parameter γ versus pressure (a) and temperature (b) for the WC.

WC的格林艾森系数γ随压强和温度的变化关系如图13(a)和13(b)所示.图13(a)给出了不同温度下WC的γ与压强的变化关系.由图可以看出，各个温度下的γ均随着压强的增大而不断地减小.如图13(b)所示，随着温度的增加，γ在增大，与γ随压强的变化关系相反.

3.6 光学性质

当电磁波通过晶体时，光子会与原子相互作用，导致吸收、散射、折射和反射等行为.而2.4中(21)-(29)的公式为分析晶体的能带结构和光学性质提供了理论基础.

复介电函数反映了固体的能带结构和各种光谱信息[40].不同能级的电子发生跃迁会产生各自对应的光谱，而各个介电谱峰可用WC的能带结构和电子态密度来解释.WC的复介电函数实部与虚部随入射光子能量的变化关系如图14(a)所示.当入射光能量E= 0时，复介电函数实部的值就表示静态介电常数，从图14(a)中的Re曲线可以看出，WC的静态介电常数为22.933.并且WC的复介电函数实部ε1(ω)随光子能量的增加，呈现出先增加后减少直至趋于平衡的变化趋势.复介电函数虚部决定着材料的光吸收特性.如图所示，WC主峰值对应的光子能量为3.358 eV，该结论对某些光学元件具有潜在的应用前景.

通过对复介电函数的虚部和实部进行计算，得到了如图14(b)所示的光学吸收系数谱.一般来说，吸收系数和复介电函数的虚部ε2有着很密切的联系.从光的吸收系数可以得知每单位长度的光强度衰减情况.在E= 43.629 eV时，吸收峰达到了最大值525570.427 cm-1.在较高能量区域，由于碳化钨的金属性，吸收系数逐渐降为零.

图14(c)显示了WC的反射率变化曲线.由图可以看出WC的静态反射率为0.428，在E= 18.647 eV时，反射率达到最大值0.506.在E= 19 eV时WC的反射率急剧下降，这表明对于不同频率的入射光，WC的响应性能变化巨大.而在60 eV以上的高能区，WC的反射率几乎为0.

折射率是光在真空中的传播速度与光在介质中的传播速度之比，可用来表示光能的衰减[25].图14(d)显示了WC的光折射率n和消光系数k随入射光能量E的变化趋势，从图中可以看到，折射谱中出现的所有峰都与介电函数虚部出现的峰有关.当光子的能量为0时，WC的静态折射率为4.789.在光子能量为26.091 eV时，折射率达到最低值，这时入射光发生折射的能力也是最弱的.而消光系数在光子能量E= 8.254 eV处取得最大值，在8.2～30 eV范围内，随着能量的增加消光系数k逐渐减小，且在E>60 eV的范围内，消光系数为0.

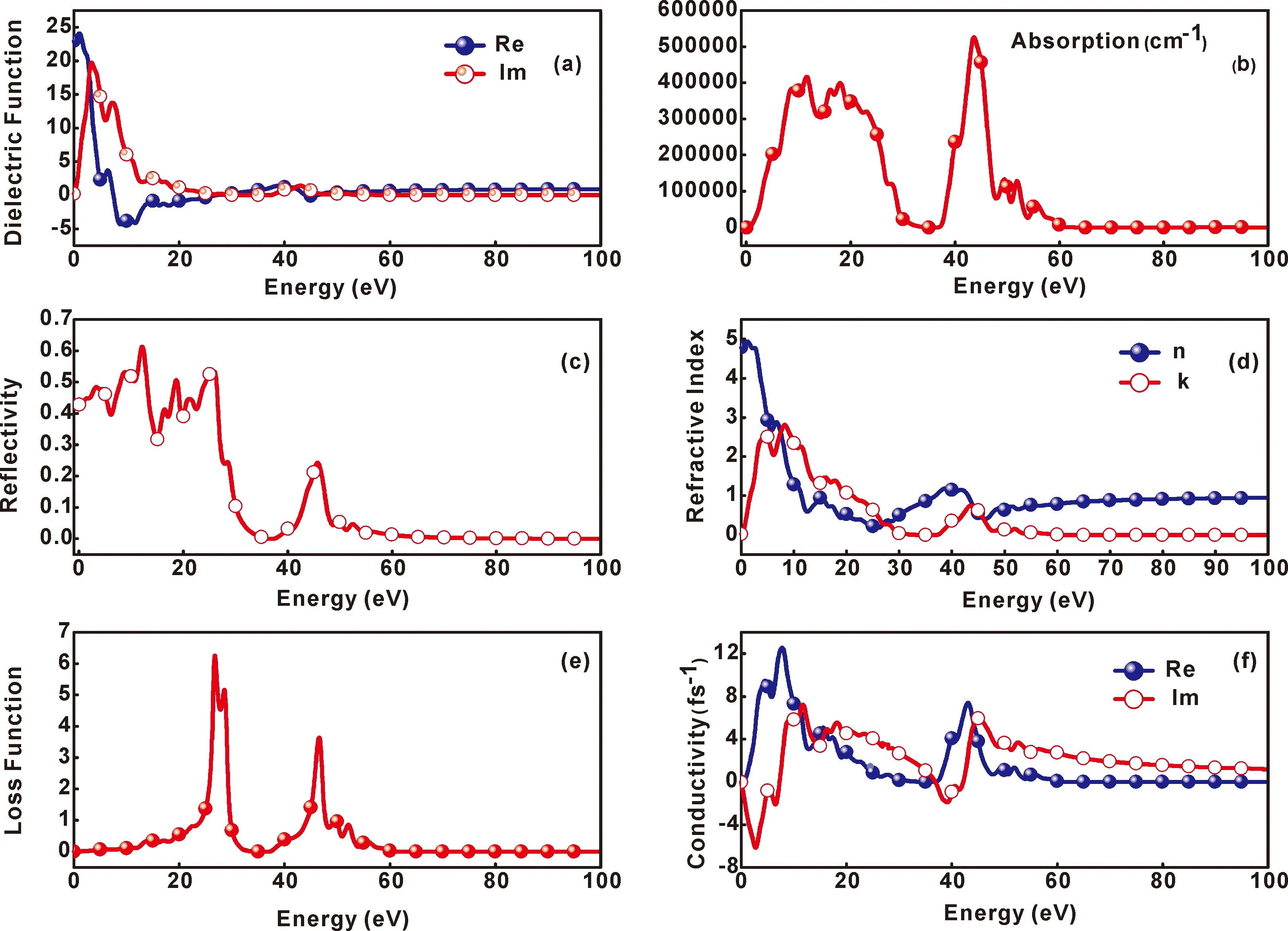
图14 WC的复介电函数 (a)、吸收系数 (b)、反射率 (c)、折射率与消光系数 (d)、损失函数 (e) 和光电导率 (f)Fig.14 Complex dielectric functions (a),absorption coefficients (b),reflectivity (c),refractive index and extinction coefficient (d),loss function (e) and conductivity (f) of WC.

损失函数主要描述的是光电子在穿过均匀电介质时的能量损失，WC的损失函数如图14(e)所示，WC有很明显的能量损失峰.区域能量损失谱的急剧上升，是由于等离子体中电磁波的相速度大于光速c，(n=c/v，因此n<1，其中n为折射率，v为等离子体中电磁波的相速度)，造成了较强的色散[41].在这种情况下，能量以焦耳热的形式释放出来，导致不同区域能量损失谱的急剧上升.

光电子材料中一个重要的参数就是光电导率，它反映了光照引起电导率改变的现象[42].图14(f)为WC光电导率的实部Re和虚部Im，由图可知，光电导率的实部有两个很明显的峰，而在E >60 eV的范围里，光电导率基本为0.

4 结 论

本文采用了基于密度泛函理论的第一性原理和广义梯度近似方法，对WC的结构进行了几何优化，得到能量最低的结构，并计算了WC的结构、弹性、声子、电子、光学和热力学性质.得到的结论如下：(1)通过研究发现WC结构的碳化钨具有最好的稳定性，计算得到的平衡晶格参数与前人的计算数据和实验值符合，说明本文的计算是可信的.(2)WC具有机械稳定性，而且有很高的硬度，证明了WC是脆性材料，它的弹性常数Cij随着压力P的增加而增大，意味着可压缩性随压力增大变得越来越困难.(3)能带结构和电子态密度的分析证实了WC的金属性，而且具有p-d杂化.(4)验证了WC的动力学稳定性，300 GPa内声子色散在整个布里渊区都没有虚频.(5)通过探索WC在不同压强、不同温度下的热力学性质可知：压强对V/V0变化影响较大；热容在高温时接近Dulong-Petit极限；给定压强下热膨胀系数α在600 K温度以上增长缓慢；德拜温度ΘD受温度的影响远小于受压强的影响；在低压下格林艾森系数γ的变化较大.(6)光学性质的研究表明，WC在高能区很难吸收光.