双模随机交错晶场对spin-1和spin-1/2混合自旋纳米管中Blume-Capel模型磁化强度的影响

李晓杰,刘延春,李新军

(齐鲁理工学院，济南 250200)

1 引 言

自1966年，Blume-Capel(BC)模型被创建之后[1,2]，人们已经利用不同方法对多种晶格上的BC模型的磁化性质、热力学性质、磁滞回线和相图进行了研究.Y.F.Zhang小组研究了外磁场和交换相互作用都遵循双模随机分布时，简立方晶格中混合自旋系统的临界行为[3].同年里，该小组又研究了外磁场遵循三模随机分布时，简立方晶格中混合自旋系统的相变行为[4].文献[5]利用有效场理论研究了简立方晶格中BC模型的补偿行为和磁化过程.文献[6]中研究了外磁场服从双峰离散分布时蜂巢晶格的相变性质，发现外磁场、晶场和自旋间交换相互作用影响系统的相变并且系统出现重入现象；文献[7]的研究表明稀释晶场对蜂巢晶格系统磁学性质和相变的影响，结果显示当晶场满足稀释分布时对系统的相变没有影响并且系统不会出现三临界现象.近几年来，纳米管渐渐成为磁热性质研究领域的一个热点，实验与理论方面都已经取得一定的研究结果.实验上，毛瑞等人以植物纤维素为模板，制备出了纳米管状SnO2材料，测试结果显示，此SnO2纳米管状材料能够提高锂离子的扩散速率，有效解决解充电放电过程中电极材料体积膨胀问题[8].文献[9]中发现Fe-Ni磁性纳米管具有明显的各项异性；理论上，Zaim小组研究了外磁场满足三模分布时纳米管上自旋为1Ising模型的磁性质和相图[10]，结果表明该系统具有一阶相变、三相临界点和二阶相变并出现重入现象.Osman等人分别讨论了纳米管中纯自旋系统的磁化强度、磁化率、热力学性质和相图[11]，讨论了晶场对系统磁热性质的影响，结果显示系统存在一阶相变和二阶相变.文献[12]利用有效场理论研究混合自旋纳米管系统的磁热特性，结果显示系统存在三临界点.文献[13]研究了Ising纳米管系统中BC模型的磁滞行为.T.Kaneyoshi 讨论了纳米管系统中外壳层和内壳层最近邻自旋间交换相互作用对磁化率的影响[14].文献[15]显示双模随机晶场中BC模型的磁化强度和相变性质，得到了系统的磁化强度与温度和双模随机晶场的关系以及相图，结果表明系统在双模随机晶场中会表现出不同的磁学性质和相变行为.文献[16]讨论了纳米管上BEG模型的热力学和相变性质，研究发现纳米管系统存在三临界点.文献[17]研究了稀释晶场作用下纳米管中BC模型的磁化性质，结果表明，稀释晶场作用下系统的内能、比热和自由能呈现出不同的磁学性质.文献[18]利用基于密度泛函理论的第一性原理方法研究了稀土金属La吸附掺杂BN纳米管的储氢性能.据我们所知，迄今人们还没有研究外磁场、晶场参数比值和双模随机交错晶场对纳米管系统平均磁化强度的影响.为了弄清楚外磁场、晶场参数比值和双模随机交错晶场对纳米管系统磁化性质的影响，本文利用有效场理论对纳米管上混合自旋BC模型格点的平均磁化强度与双模随机交错晶场取值概率、外磁场、晶场参数比值和晶场的关系进行了研究，给出了平均磁化强度随温度的变化曲线.

2 模型和方法

无限长纳米管由内壳层和外壳层两部分组成，见图1.图1(a)为纳米管的立体示意图，图1(b)给出其横截面示意图.为了更清晰地显示不同格点上具有相同配位数的磁性原子，用圆圈、方块和三角形分别代表配位数为5、6和7的磁性原子.外壳层每个磁性原子的自旋为1，内壳层每个磁性原子的自旋为1/2.图中原子间的连线代表最近邻磁性原子之间存在交换相互作用，它们的大小分别为J1、J2和J.

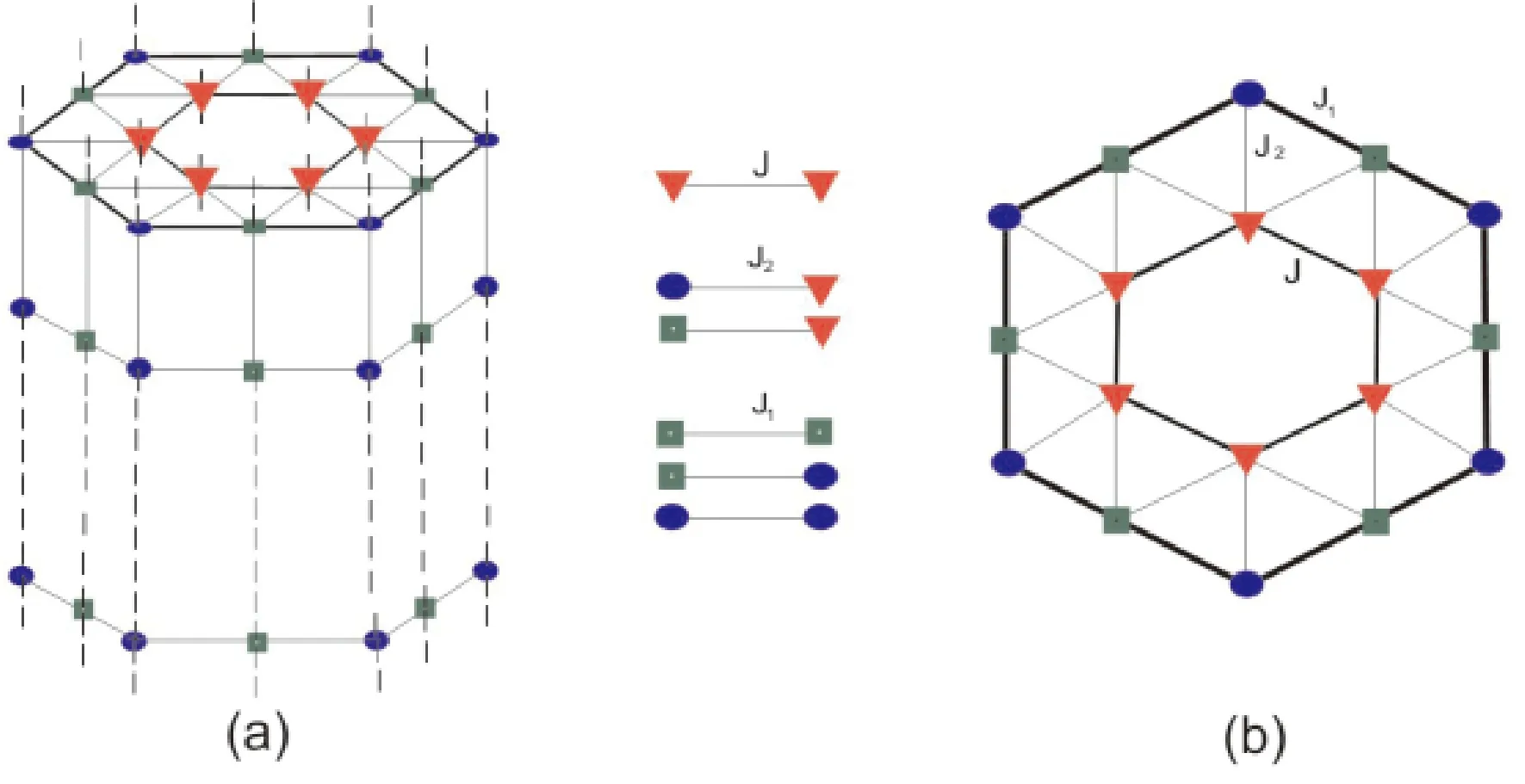
图1 纳米管示意图.(a) 立体图，(b) 截面图，圆圈和方块代表外壳层磁性原子，三角代表内壳层磁性原子，实线表示最近邻自旋间的交换相互作用.Fig.1 Theschematic pictures of nanotube:(a) perspective view of the cylindrical nanotube,(b) its cross section.The circles and squares respectively represent magnetic atoms at the surface shell.The triangles are magnetic atoms constituting the core shell.The bonds connecting the magnetic atoms represent the nearest-neighbor exchange interactions.

纳米管上BC模型的哈密顿量可表述为

(1)

其中S=-1；σ=±1/2.J1代表外壳层最近邻自旋间的交换相互作用，J2代表内壳层最近邻自旋间的交换相互作用，J2代表外壳层和最近邻的内壳层自旋间的交换相互作用，h代表外磁场，Di代表作用在格点i上的随机交错晶场，它们都满足双模晶场分布

P(Di)=pδ(Di-D)+(1-p)δ(Di-αD),

(2)

其中p(0≤p≤1)表示随机晶场取值为D的概率，1-p代表示随机晶场取值为αD的概率，α(-1≤α<0)为一无量纲参数，代表晶场强度的比值.当p=1或0时，含双模交错晶场的BC模型退化为含恒定晶场的BC模型.

利用有效场理论[19-21]可以得到外壳层格点自旋磁化强度m1和m2，内壳层格点自旋磁化强度mc的自洽方程：

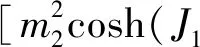
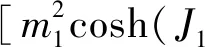
(3a)

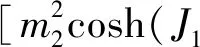
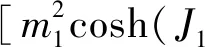
(3b)

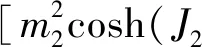
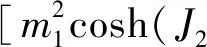
(3c)

其中函数F(x)定义为

=pf(x,D)+(1-p)f(x,αD),

(4)

(5)

函数f(x,Di)的表达式为

(6)

其中β=1/kBT，T是绝对温度，kB是玻尔兹曼常数.另外，为了整体上描述系统的磁学性质可引入平均磁化强度[22]，它的定义为

(7)

3 结果与讨论

为了便于研究，不特别说明，本文余下内容均取J1/J=J2/J=1.为了不失一般性，令外磁场h、晶场强度D和等效温度kBT以J为单位，通过求解方程(3)，给出了双模随机交错晶场作用下系统平均磁化强度随温度的变化曲线.

3.1 类对称交错晶场作用下，外磁场为零时，概率对系统平均磁化强度的影响

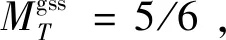
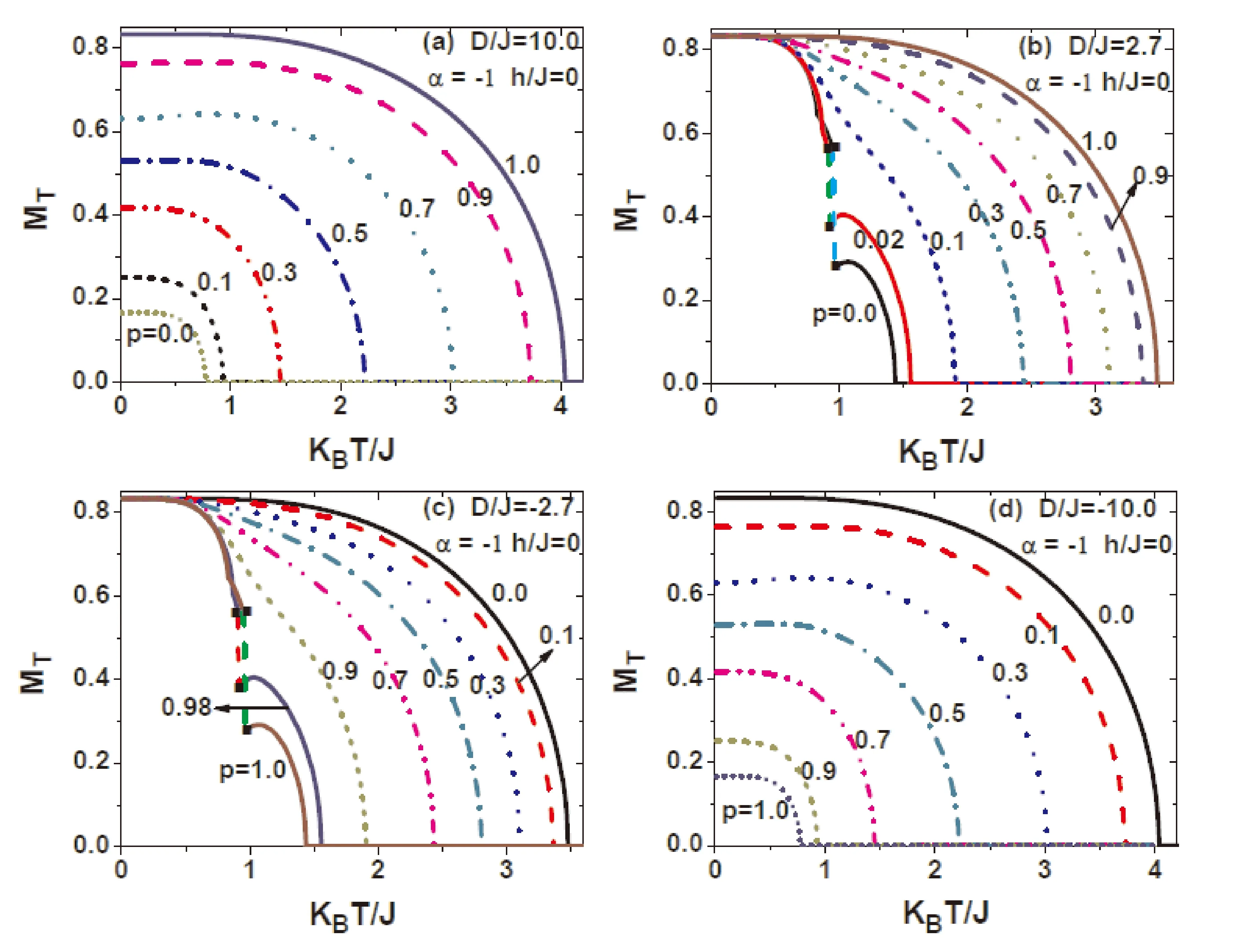
图2 外磁场为0，晶场强度比值为-1，晶场参数D/J分别为(a) 10.0，(b) 2.7，(c) -2.7，(d) -10.0时，系统平均磁化强度随温度的变化曲线，曲线上的值为随机晶场概率p.Fig.2 The temperature dependence of the magnetization is presented with some selected values of crystal field D/J (a) 10.0，(b) 2.7，(c) -2.7，(d) -10.0,when the external magnetic field is 0 and the value of D/J=-1.The real number on each curve denotes the value of p.

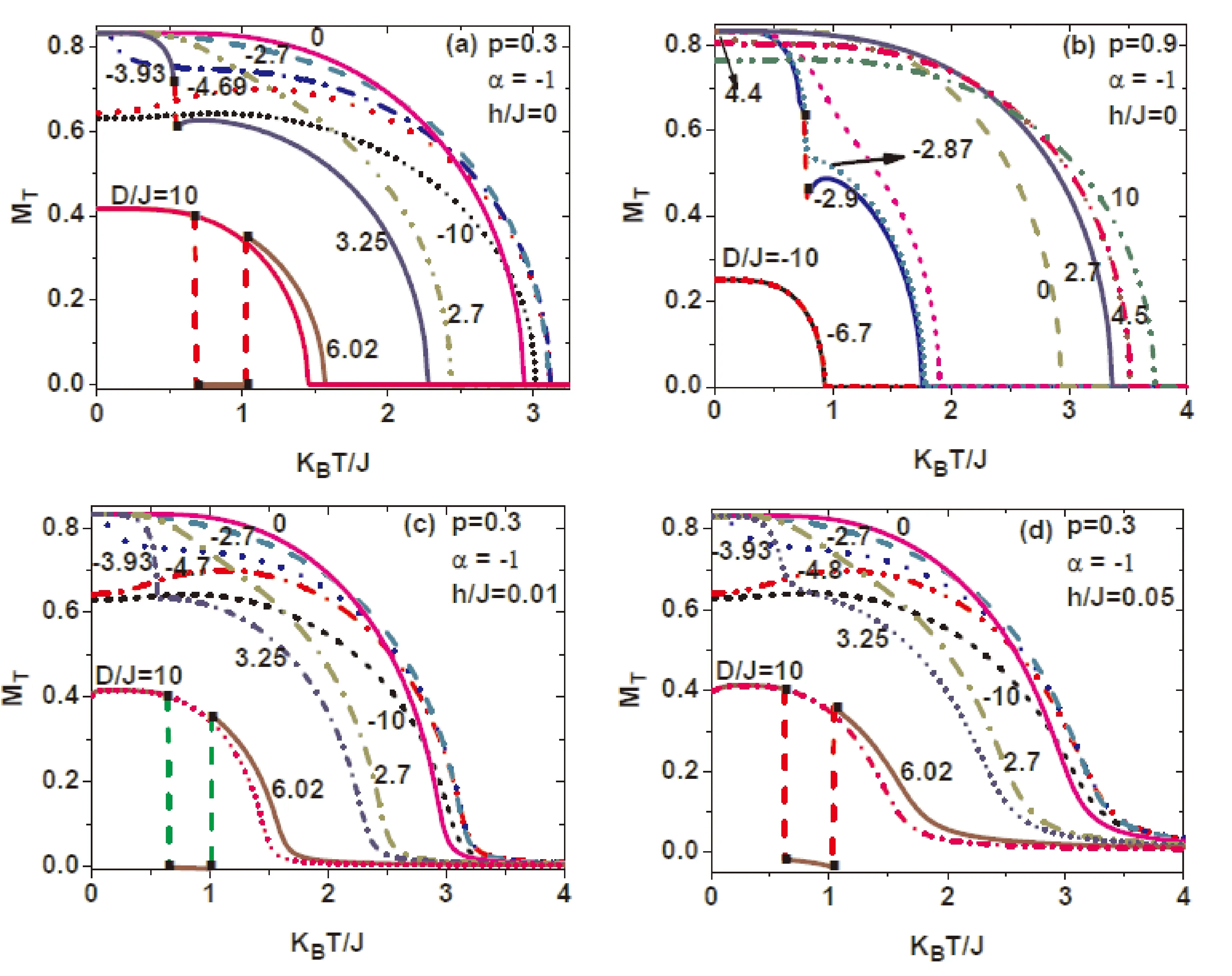
图3 概率p=0.3和0.9时，系统平均磁化强度随温度的变化曲线，曲线上的值为晶场参数D/JFig.3 The temperature dependence of the magnetization is presented with some selected values of crystal field D/J,when the external magnetic field is not zero.The real number on each curve denotes the value of D/J

3.2 类对称交错晶场作用下，晶场参数和外磁场对系统平均磁化强度的影响

为了研究不同晶场强度下系统平均磁化强度随温度的变化情况，图3(a)和(b)分别给出了p=0.3和0.9时，双模随机交错晶场分布下平均磁化强度随温度的变化曲线.结果表明，p较小时，负晶场对磁化强度阻碍作用不明显；晶场参数取正值时，系统发生一级相变；系统平均磁化强度出现缺失现象(平均磁化强度为零)；当D/J=-3.93且温度较低时，磁化强度随温度的变化非常明显，通过研究，我们认为是因为外壳层格点(蓝色圆点代表的磁性原子)的配位数较小的原因.随着p增大，负晶场对系统磁化强度抑制作用明显，晶场参数取负值时，系统发生一级相变.虽然不同晶场强度作用下，系统平均磁化强度呈现出不同的磁化现象，但总体变化趋势相似.为了研究外磁场对平均磁化强度缺失现象的影响，我们给出了图3(c)和(d).从图中可以看出，外磁场能够减弱平均磁化强度缺失现象，但是缺失部分平均磁化强度呈现负值.

3.3 类非对称交错晶场作用下，外磁场为零时，概率对系统平均磁化强度的影响

图4(a)—(f) 给出了晶场满足类非对称交错晶场(例如α=-0.5)分布时，系统平均磁化强度随温度的变化曲线.图4(a)和(b)及图4(d)和(f)显示，系统平均磁化强度随温度的变化曲线与图2相似.但是当D/J=-5.8时，系统平均磁化强度随温度变化曲线局部出现负值(例如p=0.7,0.9,1.0)，见图4(e)，说明原子掺杂程度(晶场强度比值α)不同，会使系统呈现出不同的磁化现象.

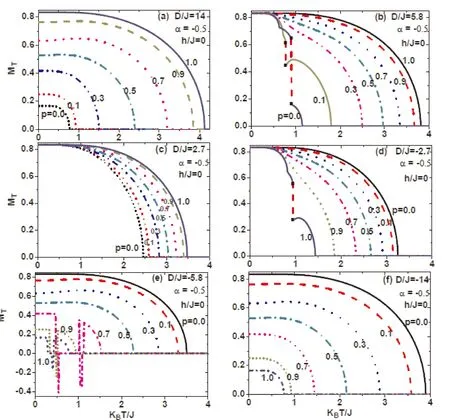
图4 外磁场为0，晶场参数D/J分别为(a) 14，(b) 5.8，(c) 2.7，(d) -2.7，(e) -5.8，(f) -14时，系统平均磁化强度随温度的变化曲线，曲线上的值为随机晶场概率p.Fig.4 The temperature dependence of the magnetization is presented with some selected values of D/J=14,5.8,2.7,-2.7,-5.8,-14,when the external magnetic field is 0.The real number on each curve denotes the value of p.

3.4 类非对称交错晶场作用下，晶场参数和外磁场对系统平均磁化强度的影响

为了研究不同晶场强度比值对系统平均磁化强度的影响，图5给出了类非对称交错晶场作用下平均磁化强度随温度的变化曲线.结果显示：概率较小和较大时，系统都存在一级相变和二级相变；外磁场较小时，没有对系统平均磁化强度产生明显的影响.但是系统平均磁化强度出现缺失和负值的现象更加明显.我们认为导致这种现象的物理原理是不同原子掺杂，使得系统在一定条件下平均磁化强度出现负值.

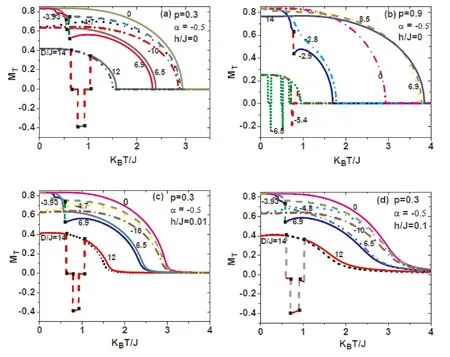
图5 概率 p分别为0.3，0.9时，系统磁化强度随温度的变化曲线，曲线上的值为晶场参数D/JFig.5 The temperature dependence of the magnetization is presented with some selected values of the probability of p =0.3,0.9,when the external magnetic field is not zero.The real number on each curve denotes the value of D/J.

4 结 论

本文利用有效场理论研究了双模随机交错晶场作用下spin-1和spin-1/2混合自旋BC模型系统的平均磁化强度随温度的变化情况.结果表明，系统格点的平均磁化强度与随机交错晶场的取值概率p、晶场强度比值α、晶场参数D/J、外磁场、温度以及交换相互作用密切相关.概率P、外磁场、晶场强度比值和D等诸多因素相互竞争，使系统表现出比恒定晶场作用的BC模型更为丰富的磁化现象：系统格点的平均磁化强度随温度的变化曲线呈现缺失和负值的现象；P、α和D/J会影响系统的一级相变和二级相变.