应用多普勒牵引的高分辨率星载SAR滑动聚束模式设计方法
郝梁 肖枫 张润宁 程博文 禹霁阳
(1 北京空间飞行器总体设计部,北京 100094)(2 北京理工大学,北京 100081)
星载SAR可以分为聚束、条带、扫描等多种成像模式[1],以适应不同的成像需求。根据SAR工作原理,距离向分辨率可以通过增加发射信号带宽提高,方位向分辨率可以通过减小方位向天线孔径长度提高[2],但为了满足系统增益要求,合成孔径长度不能无限增大。为获得更高的方位向高分辨率,同时兼顾方位向测绘幅宽,形成了一种常用的高分辨率星载SAR工作模式——滑动聚束模式。滑动聚束模式(SSM)其实是条带模式与聚束模式的混合模式,其方位向测绘带宽大于聚束模式,同时方位向分辨率优于条带模式,可以精确获取局部区域的重要信息[3]。
文献[4]中研究了聚束模式卫星姿态机动策略,可应用到敏捷SAR平台的滑动聚束模式设计中。2014年德国“X频段陆地合成孔径雷达”(TerraSAR-X)卫星曾进行过高分辨率聚束SAR试验,通过方位向大幅度一维电扫描的方式实现了聚束模式,该聚束模式分辨率约0.2 m,方位向幅宽约4.5 km,聚束时间约8 s[5-6]。文献[7]中研究了滑动聚束模式卫星二维姿态机动策略,该策略采用基于虚拟焦点的滑动聚束模式设计,并通过地面仿真的方式验证该模式设计方法的可行性。但是,在实际工程应用过程中,由于高分辨率SAR滑动聚束模式斜视角较大,星载弯曲几何模型对成像造成的影响不可忽略。斜视角变大后,多普勒中心沿方位向时变将呈现出非线性变换,导致方位频谱解混叠无法完成。
针对上述问题,本文充分考虑星载SAR实际工况条件下的非理想因素,在模式设计时采用多普勒校正抵消多普勒中心时变的非线性变换,而且模式设计方法得到的回波数据可以利用传统的非线性调频变标(NCS)算法进行成像处理。利用仿真平台对设计方法进行仿真,并通过回波仿真与成像的方式验证了设计方法的有效性。
1 高分辨率滑动聚束模式设计方法
如图1所示,滑动聚束模式中波位并不是固定的,而是沿方位向移动,但是波位移动速度小于平台移动速度[8]。SAR的方位向分辨率是由平台运动产生的多普勒带宽决定,而方位向幅宽与合成孔径时间有关,因此需要根据各种参数要求综合设计。本文提出一种应用多普勒牵引实现高分辨率星载SAR滑动聚束模式设计方法。首先,根据输入参数确定成像场景位置和幅宽;然后,以多普勒为牵引校正姿态角;最后,根据校正完的姿态角完成波位参数计算。其过程共包含滑动聚束连续工作时间计算、多普勒校正、成像姿态和波位参数计算4个主要步骤,如图2所示。
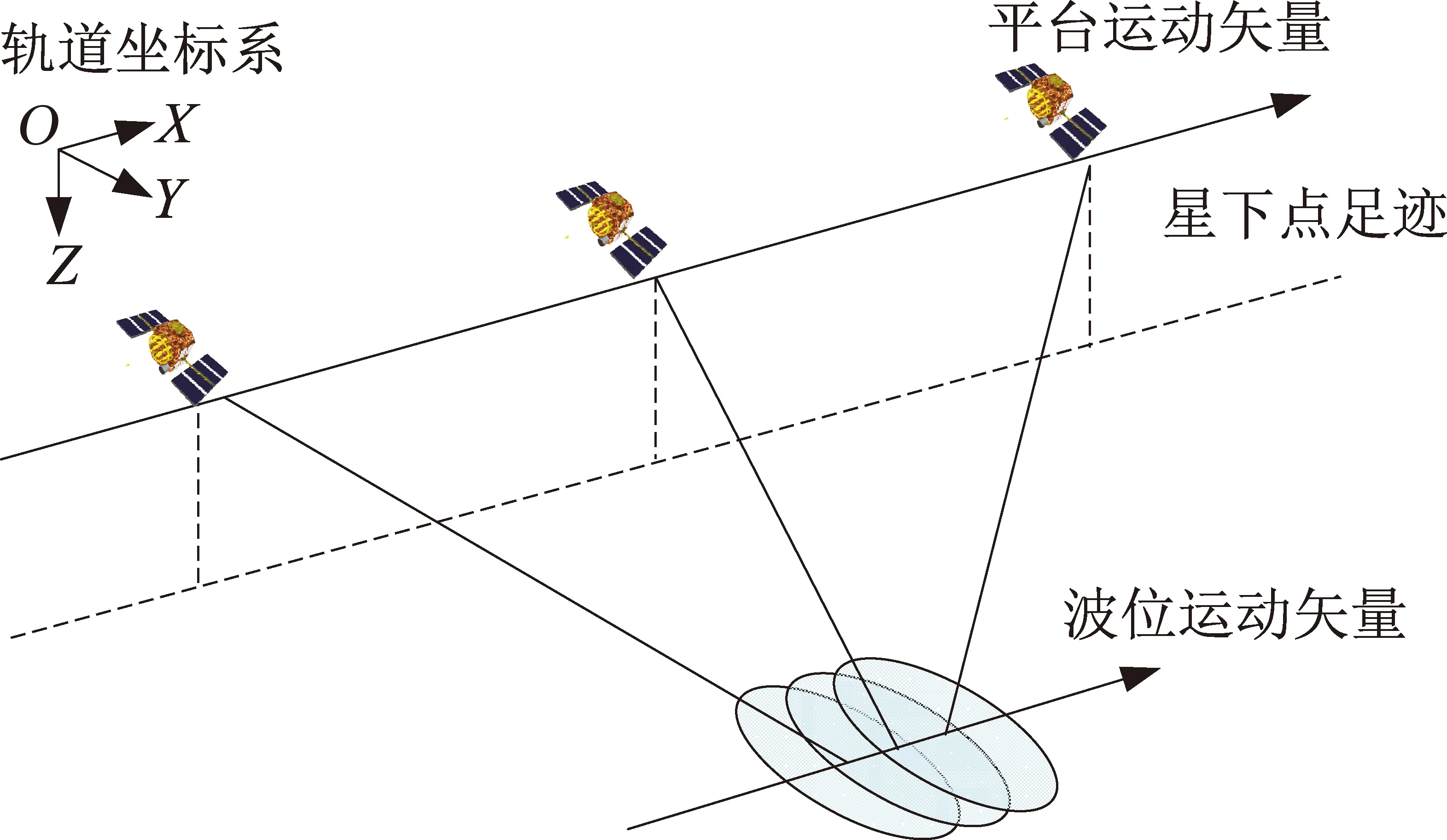
图1 滑动聚束模式波位
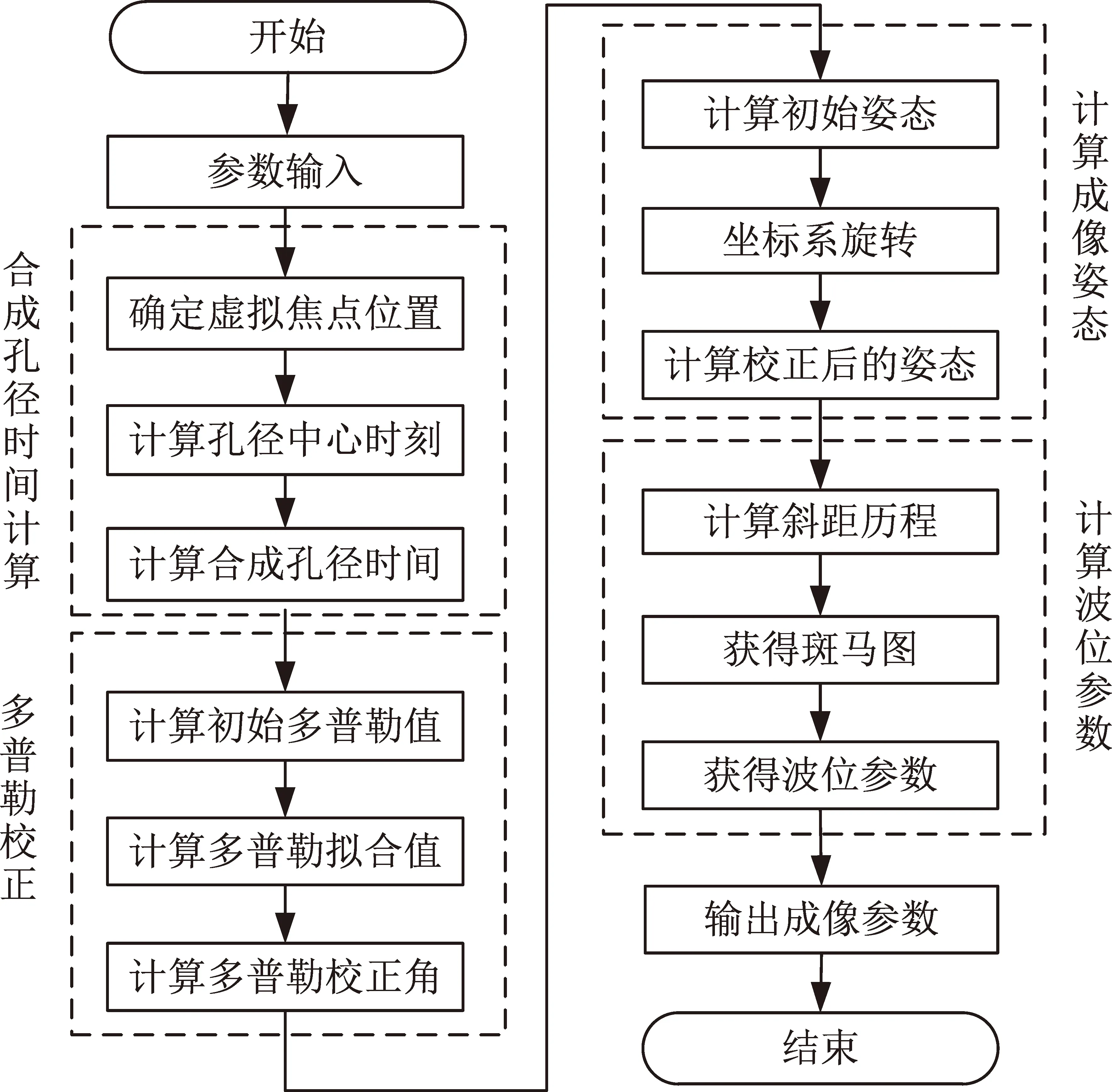
图2 模式设计方法流程Fig.2 Mode design method flow
1.1 滑动聚束连续工作时间计算
假设平台速度为Vs,回波的方位向带宽为Ba,则方位向分辨率为
(1)
式中:Ba=Ka·Ta,多普勒调频斜率Ka=2Vs2·cosθc/(λ·Rc),θc为孔径中心的斜视角,λ为波长,Rc为孔径中心的斜距,合成孔径时间Ta=λ·Rc/(D·Vg·cosθc),D为天线方位向长度,Vg为波位速度。
由此可见,滑动聚束模式方位向的分辨率为条带模式的Vg/Vs倍[9-10],而条带模式和聚束模式可以理解为Vg=Vs或Vg=0的特殊情况的滑动聚束模式。本文为简化滑动聚束模式的设计过程,采用虚拟焦点计算法,即假设孔径中心时刻平台位置与虚拟焦点的距离为Rrot,则定义滑动聚束因子为
(2)
在滑动聚束连续工作时间较小的情况下,可以近似认为
(3)
即对于左右对称的滑动聚束模式,其方位向分辨率为
(4)
假设要求测绘场景方位向幅宽为Ra,所需滑动聚束连续工作时间为T,则Vg·T=Ra,最终可得[11]
(5)
1.2 多普勒校正
虚拟焦点法计算得到的姿态仅适应于旋转角较小的情况。其主要原因是:在高分辨率滑动聚束情况下,随着滑动聚束连续工作时间的增大,多普勒中心(fdc)历程呈非线性变化,这将导致成像处理过程中方位向去斜操作无法完成。
假设卫星在地固坐标系下的位置矢量为Ps(t),速度矢量为Vs(t),速度矢量与波束指向的夹角为θ(t),场景在地固坐标系的位置矢量为O(t),则波束指向矢量(即卫星Z轴指向)可表示为
(6)
速度矢量与波束指向的夹角为
(7)
孔径各时刻的fdc(t)=2Vs(t)·cosθ(t)/λ[12],得到孔径起止时刻tstart和tend的多普勒中心,做拟合后即得到整个孔径各个时刻tstart和tend的多普勒拟合值。多普勒校正通过在方位向上微调波束指向改变θ(t)的方式实现,使整个孔径内的多普勒中变化曲线与拟合值一致。校正后可以保证多普勒中心历程为一条直线。校正前和校正后的多普勒中心如图3所示。

(8)
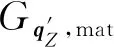

图3 多普勒校正曲线Fig.3 Doppler correction curve
1.3 计算成像姿态
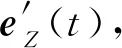
(9)
根据右手定则,可以求出t时刻卫星本体坐标系X轴单位矢量为
(10)
最终得到的卫星本体坐标系3轴指向e(t)可表示为[eX(t)eY(t)eZ(t)]T,通过矩阵变换可以求出卫星平台各个时刻的姿态角,即
[θYawθPitchθRoll]T=
Gq′,angle(Gmat,q′([eX(t)eY(t)eZ(t)]T))
(11)
式中:θYaw,θPitch,θRoll分别为卫星平台的偏航角、俯仰角和滚动角;Gq′,angle为四元数到欧拉角的转换函数,为方便计算,以1-2-3转序定义,即得到1-2-3转序下的卫星平台3轴姿态角。
1.4 计算波位参数
与普通滑动聚束模式不同[14-15],高分辨率滑动聚束模式的波位参数需要进行变重频操作,主要原因是虽然某一时刻的瞬时回波距离跨度范围仅为几十千米,但整个成像过程中的作用距离范围移动高达上百千米,这时单个波位已无法满足整个场景范围的有效覆盖,必须在成像过程中进行变重频来移动回波窗,从而适应回波的距离徙动。
根据前文得到的姿态参数及几何模型,计算得到整个孔径范围的斜距历程,并在斜距/重频表(斜距斑马图)上找出不同时间段内合适的波位参数,即可得到系统所需的变重频时序及起始采样时刻,即完成高分辨率滑动聚束成像模式的设计。
2 设计实例与仿真验证
为验证上述设计方法的有效性,本节通过STK和Matlab软件建立联合仿真实验平台进行仿真验证。首先,利用STK软件建立一组典型成像过程的星地几何模型;然后,利用Matlab软件读取STK软件模型参数。根据输入参数和本文方法进行模式设计,最后将姿态数据、波位参数导入到回波仿真平台中,通过完成点目标场景的回波仿真与成像验证设计结果的正确性。整个仿真验证过程如图4所示,该滑动聚束模式仿真输入参数如表1所示。
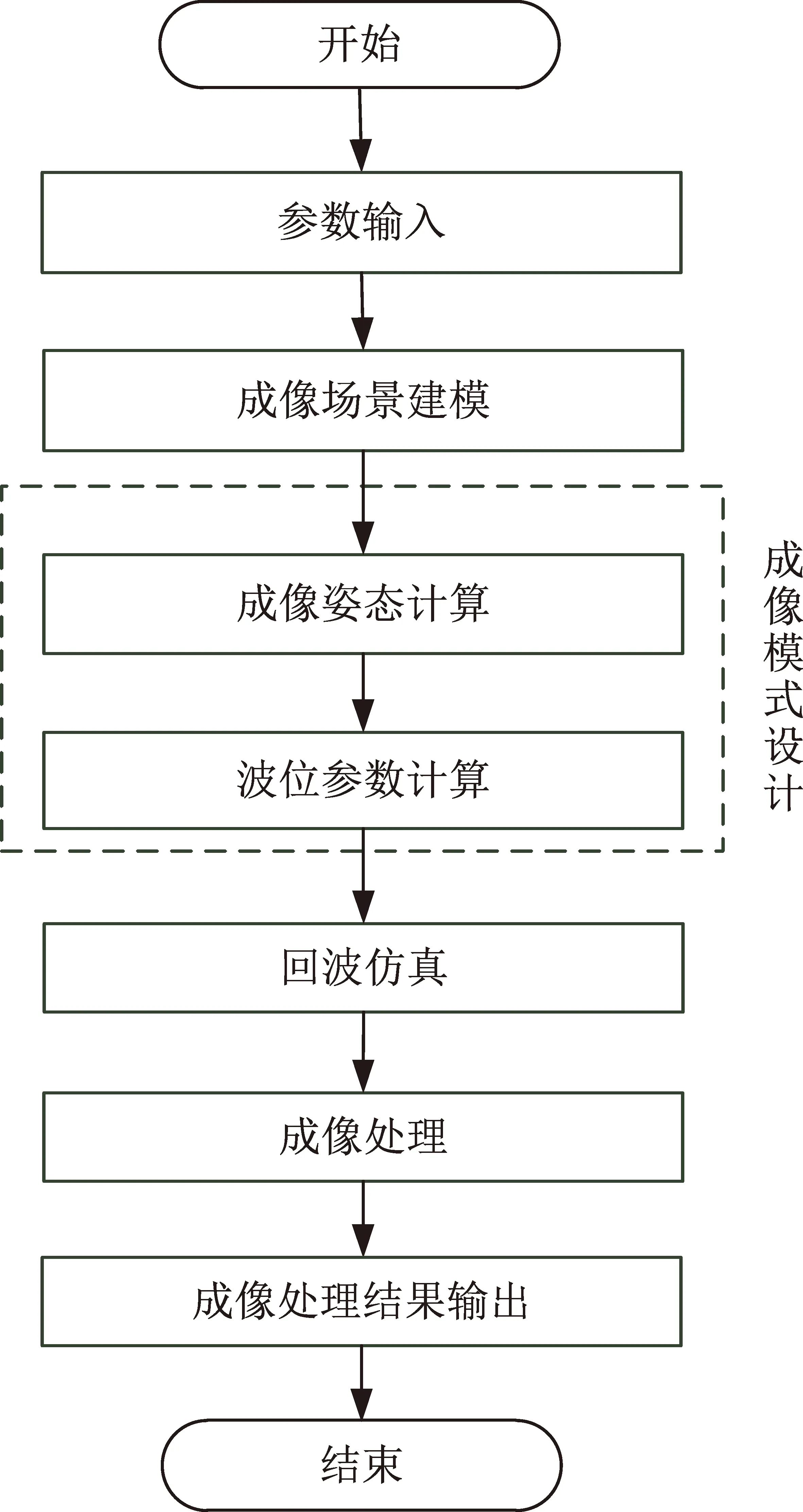
图4 仿真验证流程
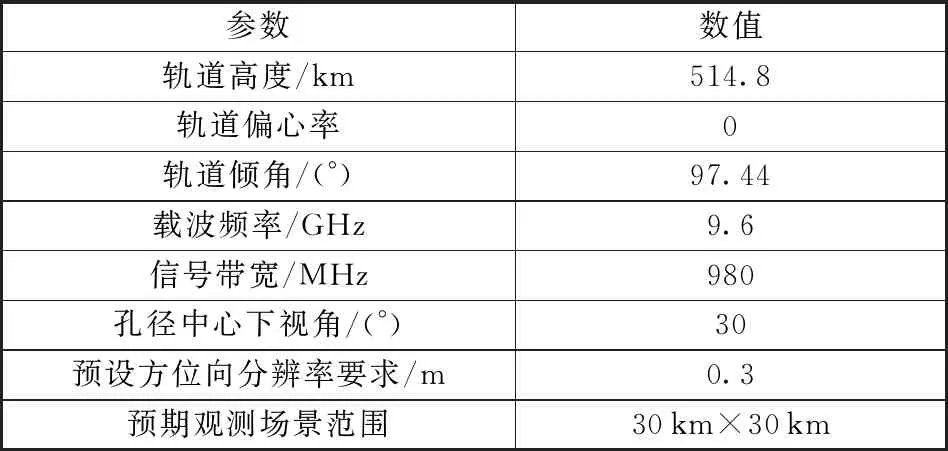
表1 输入参数
2.1 成像姿态设计结果
孔径起止时刻,控制波束指向场景的边沿位置,见图5。整个孔径范围内需要通过对波束指向微调的方式校正多普勒中心历程,校正姿态如图6所示,校正结果如图7所示。经仿真分析,在卫星平台姿态精度0.01°的情况下,多普勒中心fdc历程的校正误差约为20 Hz,已远小于多普勒采样率,去斜处理后该频率误差可忽略。根据计算得到的孔径起止时刻位置,在完成多普勒中心校正后,可以得到成像所需的3轴姿态,校正后的姿态角变化曲线见图8。

图5 STK软件中波束覆盖范围Fig.5 Beam coverage area in STK
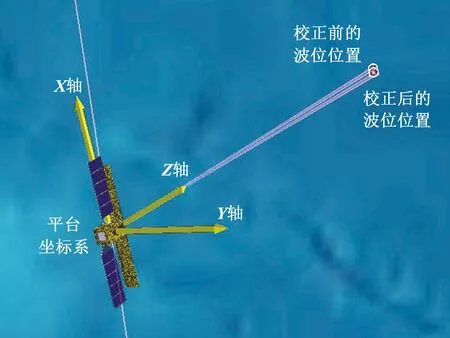
图6 多普勒校正姿态Fig.6 Doppler correction attitude

图7 多普勒校正结果Fig.7 Doppler correction result
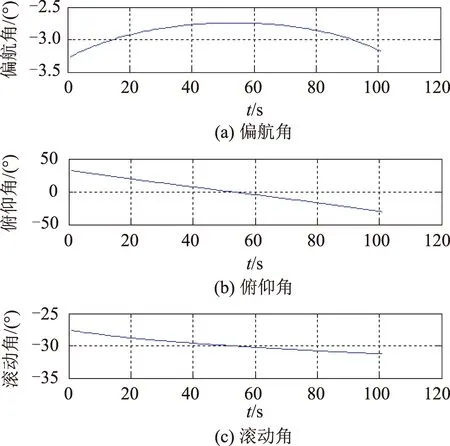
图8 姿态角变化曲线Fig.8 Attitude angle variation curve
高分辨率滑动聚束模式成像的合成孔径时间需要100 s,在成像过程中,俯仰角变化范围达60°,为波束指向调整的主分量;卫星滚动角变化量大于4°,主要用于调整波束的远近,使波束中心在地面的移动轨迹为一条直线;偏航角变化范围约0.8°,用于确保波束多普勒平面与天线方位轴垂直。
2.2 波位参数设计结果
由于每次变重频都会造成一定数量的回波损失,因此要求变重频次数尽量少。如图9所示,在最小次数的原则下,共需要18次变重频操作覆盖整个斜距变化范围,同时系统需要通过实时更新采样起始时刻适应回波斜距的大距离徙动。由图9可以看到,18次变重频的波位参数均已避开发射脉冲干扰和星下点回波干扰。
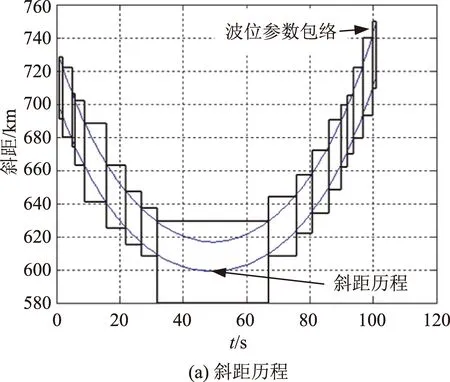
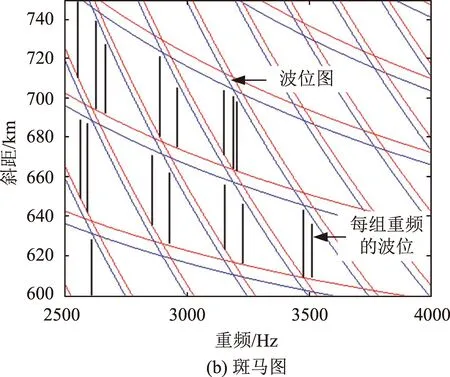
图9 波位参数设计结果Fig.9 Beam position parameter design result
2.3 回波数据成像结果
将上述仿真生成的姿态信息与波位参数信息导入到回波仿真软件中,仿真场景点目标设置如图10所示,目标场景幅宽约25 km×25 km,每个目标都可以被波束完整覆盖,保证每个点目标的积累时间。
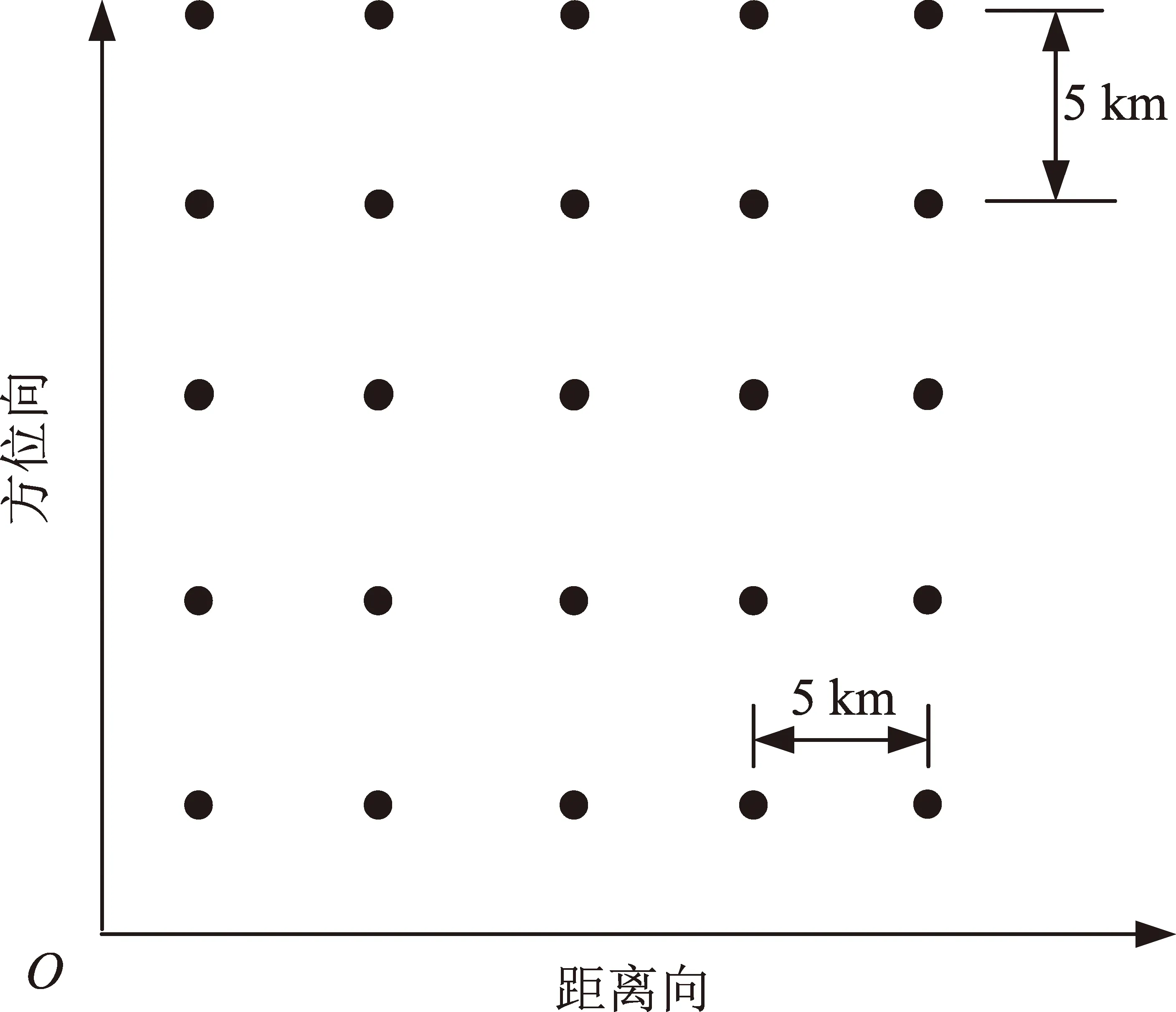
图10 0.3 m分辨率滑动聚束点目标分布
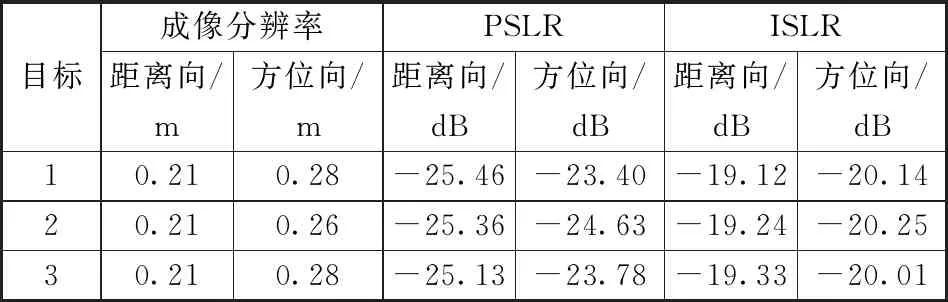
成像采用了去斜+距离NCS实现滑动聚束成像。算法包括方位向去斜预处理和距离向NCS算法处理[16],因此需要设计针对高分辨变重频成像算法。算法的主要流程是将变重频信号插值成均匀信号,然后进行方位向信号升采样,接着利用NCS算法进行距离压缩和距离徙动校正,最后进行方位向压缩。成像结果如图11所示,从表2的统计中可以看出,点目标聚焦良好。成像分辨率、峰值旁瓣比(PSLR)和积分旁瓣比(ISLR)指标均满足SAR成像的一般要求。
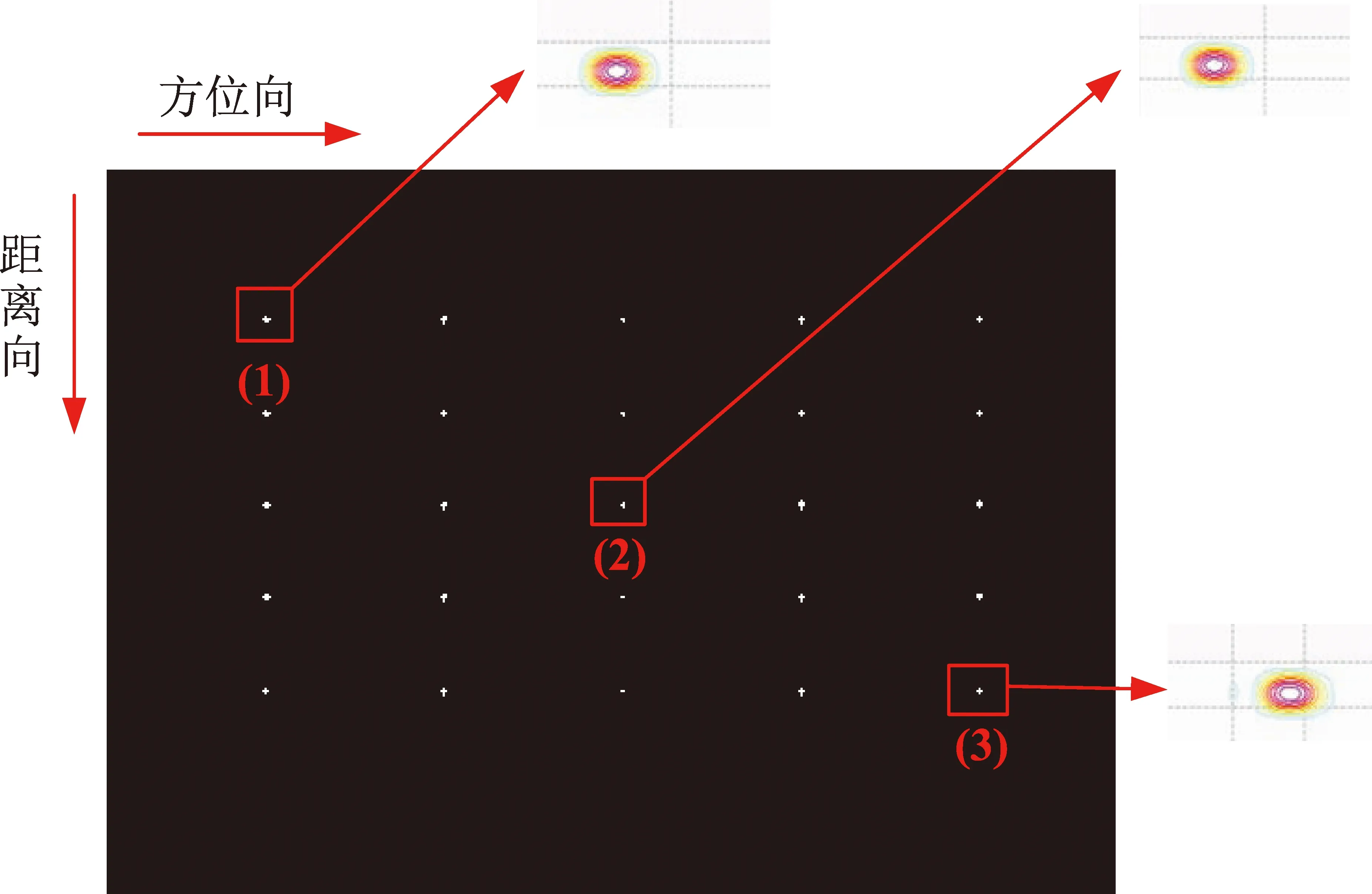
图11 点目标成像结果Fig.11 Imaging results of point target
表2 点目标成像结果
Table 2 Imaging results of point target
目标成像分辨率PSLRISLR距离向/m方位向/m距离向/dB方位向/dB距离向/dB方位向/dB10.210.28-25.46-23.40-19.12-20.1420.210.26-25.36-24.63-19.24-20.2530.210.28-25.13-23.78-19.33-20.01
传统设计方法下设计的高分辨率滑动聚束模式,其回波的多普勒中心呈非线性变化,导致成像处理困难。经过仿真验证可知:本文提出的设计方法能校正回波的多普勒中心,使回波可以利用标准的NCS算法求解。在预设场景下,整个场景的分辨率都优于0.3 m,表明本文设计方法解决了多普勒中心非线性时变导致传统频域成像算法无法成像的问题。
3 结束语
本文提出了一种应用多普勒牵引的高分辨率星载SAR滑动聚束模式设计方法,利用多普勒牵引完成长孔径滑动聚束模式设计,解决了星地弯曲几何模型造成的多普勒非线性变化问题,可应用于基于卫星平台姿态机动实现高分辨率星载SAR成像。经过仿真验证,该设计方法得到的回波数据可以用传统频域成像方法完成成像处理,极大降低了高分辨率模式的图像处理难度,可为我国高分辨率SAR卫星成像模式设计提供参考。

