基于矩阵加权方法的非线性异步融合估计器设计①
王 波 周 康 朱加民
(*义乌工商职业技术学院机电信息学院 义乌 322000) (**浙江工业大学信息工程学院 杭州 310023)
0 引 言
融合估计就是对来自多个传感器的数据按照某种规则进行整合、计算和优化,从而获得比单一传感器更精确、更全面的状态信息或者更精确的估计值[1]。近些年来,随着信息技术的快速发展,传感器的性能和计算机运算能力都得到了很大提高,使得融合估计广泛应用于目标跟踪、信号处理、故障检测以及网络安全等诸多领域[2-4]。然而,无线网络化多传感器系统的大规模引入虽然具有覆盖范围广、成本低、鲁棒性好等诸多优点,但是也带来了一系列待解决的问题,如能量受限、带宽约束、信号采集和传输不同步等[5,6]。
通常,可以根据融合估计所融合信息来源的不同将其拆分为观测融合和状态融合,即融合观测信息的一部分为观测融合,融合状态信息的一部分为状态融合。进一步地,观测融合方法可按照传感器采样是否时间同步分为同步情况下的估计方法和异步情况下的估计方法。与同步观测融合方法相比,异步融合方法可以更好地处理异步采样信息,且具有更广泛的使用范围、更符合实际工程问题等优点[7]。目前,针对异步采样下的观测融合估计问题已经有一些研究成果,如文献[8]提出了一种适用于传感器多速率采样下的异步观测融合估计方法。文献[9]在传感器量测具有衰退性的时变不确定系统上,提出了一种分布式融合估计方法。文献[10]提出了一种适用于具有相关量测噪声系统上的多速率异步估计器。在状态融合部分,通常的融合方法有矩阵加权融合方法和协方差交叉(covariance intersection, CI)融合方法,且在线性系统中由于矩阵加权融合方法考虑了局部估计误差之间是相关的,对信息的利用更为完整,具有较CI融合方法更高的估计精度。针对较多的局部估计值会导致批处理融合方法计算量较大的情况,文献[11]和[12]分别提出了一种序贯式CI融合估计方法和序贯式矩阵加权融合方法,且都证明了在线性系统下序贯式处理方式可以得到和批处理融合相同的估计精度、更小的计算复杂度。此外,文献[13]提出了一种适用于分簇传感器网络下的序贯融合估计算法,在融合时刻采用序贯式矩阵加权融合方法得到最终的融合估计值。然而,上述方法大都建立在线性系统上,且在使用序贯式CI融合方法或者序贯式矩阵加权算法时,融合的状态信息都是当前融合时刻的局部估计值,即可以认为上述的状态融合方法是一种时间同步的状态融合方法。而在实际应用场景中,如目标跟踪,通常很难保证局部估计值都是时间同步的,且非线性情况常常是不能避免的。因此,研究非线性系统下的异步状态融合估计器具有重要价值。
本文在解决异步采样下的非线性融合估计问题时,先通过平方根容积卡尔曼滤波器(square root cabature Kalman filtinG, SRCKF)滤波[14]方法计算出融合周期内各个传感器采样时刻的状态局部估计值,再利用状态方程传递方式将各个采样时刻的局部估计值进行同步处理。最后,在估计误差协方差迹最小的准则下推导出了异步矩阵加权状态融合估计方法,并给出了相对应的互协方差矩阵的计算方法。 仿真验证了所提出的异步矩阵加权融合算法的估计精度比标准的SRCKF高。
1 问题描述
考虑如下非线性离散随机系统:
x(Tk+1)=f(x(Tk))+w(Tk)
(1)
式中,Tk为离散时间,x(Tk)∈Rn为系统的状态,w(Tk)∈Rnw为零均值、协方差阵为Qw的高斯白噪声,用tsys=Tk+1-Tk表示系统状态更新的时间间隔,用Zs={1,…,m}表示传感器网络中有m个传感器。如图1所示,为了解决传感器异步采样引发的时钟不同步问题,用tk(k=0,1,2,…)表示融合估计时刻,然后用tfus=tk+1-tk表示融合估计周期,用tk,1,tk,2,…,tk,i分别表示在融合时间间隔(tk,tk+1]内第i个传感器的采样时刻。下式为系统式(1)的非线性异步采样量测模型:
zi(tk,i)=hi(x(tk,i))+vi(tk,i)
(2)
式中,i∈Zs,zi(tk,i)∈Rnz表示第i个传感器在时刻tk,i的量测值,vi是零均值、协方差阵为Ri的高斯白噪声,并且假设vi之间互不相关,且与系统噪声ω也不相关。
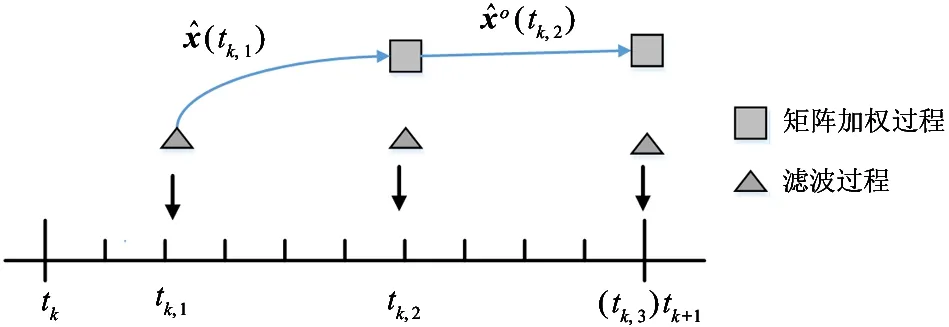
图1 非线性异步融合估计器的时序图
在上述传感器异步采样下的非线性融合估计问题中,由于局部估计值产生的时序不同,而标准的状态融合方法都要求局部估计值是对同一时刻的状态估计,此时标准的状态融合方法无法直接适用。本文目的是针对所考虑的局部估计值时间不同步的非线性系统,利用异步的量测信息,设计一个最小方差意义下的非线性异步融合估计器。
2 非线性异步融合估计器
本小节主要讨论非线性异步融合估计器的设计。如图1所示,在每个传感器采样时刻进行滤波计算,且从第2个传感器采样时刻开始进行异步矩阵加权融合计算。为此,下文先给出了非线性异步融合估计器的算法执行过程,然后基于SRCKF方法推导出了一种新的异步矩阵加权融合方法去处理异步的局部估计值。
2.1 非线性异步融合估计器的设计
针对传感器异步采样问题,以SRCKF滤波方法和矩阵加权方法为基础,设计了一种适用于融合异步状态信息的非线性异步融合估计器。如图1所示,在融合时间间隔(tk,tk+1]中,令tk,1 (3) 其中,dni=(tk,i-tk)/tsys,表示tk,i时刻和tk时刻之间间隔的系统状态间隔;Xr(tk,i)是容积点;r=1,2,…,2n;n为系统状态的维数。 (4) 其中,d2=(tk,2-tk,1)/tsys。 (5) 其中,σ=(tk+1-tk,m)/tsys,表示最后一个传感器采样时刻和融合时刻间隔的系统状态更新间隔数目。 由于SRCKF方法在滤波过程中直接以协方差阵的三角分解因子进行递推计算,这样不但能降低计算负担,提高算法计算效率,而且可以保证协方差阵的非负性,提高了滤波器的数值稳定性。 标准的矩阵加权融合方法是建立在线性系统系统上,且每个局部估计值是时序同步的。然而,上述非线性异步融合器中矩阵加权2个估计值中的一个是从上一个传感器采样时刻预测得到的。针对融合时序不同步的局部估计值问题,下面给出了异步矩阵加权融合估计器的具体实现。为了简便起见,在推导过程中省略了一些时间下标。由上述定义,异步矩阵加权融合估计器由定理1给出。 (6) (7) (8) (9) (10) (11) (12) 如此,则定理1得证。 为验证非线性异步融合估计算法的有效性,考虑在2维平面做匀速圆周运动的目标跟踪实例,其运动学模型为 其中,系统状态为xk=[px,py,θ]T,px、py和θ分别是移动目标在X轴、Y轴的坐标和圆心角,V和R分别表示匀速圆周运动的角速度和半径,仿真中设定V=0.5,R=2,tsys=0.1 s,系统噪声方差阵Q=0.008×In。 为了简便,考虑无线传感器网络中有3个测距传感器的情况,其量测方程为 +vi(tk,i) (13) (14) 式中,N表示蒙特卡洛仿真的次数。 如图2所示,与直接使用SRCKF估计器得到的状态估计值相比,异步矩阵加权融合估计器的RMSE较小。因此,异步矩阵加权算法既可以处理异步的局部估计值,又可以提高系统状态估计的精确性。 图2 异步矩阵加权融合与SRCKF的RMSE对比图 针对多传感器异步采样、传输下的非线性融合估计问题,本文设计了一种基于异步矩阵加权融合方法的非线性异步融合估计器。该估计器用SRCKF滤波方法得到采样时刻的估计值,然后在标准矩阵加权方法的基础上,提出了一种新的异步矩阵加权方法,得到最终的融合估计值。由于考虑了局部估计之间时序不同步的情况,因此,具有较大的实际应用价值。仿真结果也表明了该算法在处理非线性异步融合估计问题时的有效性。

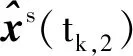

2.2 异步矩阵加权融合估计器的设计




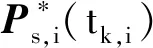


3 仿 真

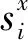

4 结 论

