改进粒子群优化小波阈值的矿用钢丝绳损伤信号处理方法研究

田 劼，宋 姗

(中国矿业大学(北京) 机电与信息工程学院，北京 100083)

钢丝绳具有弯曲性能好、结构多样、承受载荷能力强等优点，被广泛应用在煤炭运输过程中，但由于长期工作其会存在断裂的安全隐患。钢丝绳无损检测技术是在不损害钢丝绳的基础上，通过检测信号来判断损伤类型和损伤情况，目前常用的是电磁检测法。由于在检测过程中受到检测环境和现场条件等因素的影响，检测信号中存在多种噪声信号，无法对特征值信号进行提取，所以消除噪声是矿用钢丝绳无损检测的关键。小波分析是近年发展起来的一种新的时频分析方法。文献[1]利用小波分析对损伤信号实现降噪，克服传统滤波方法的不足。文献[2]提出一种改进的阈值函数，去噪效果比软、硬阈值有所改进。本文针对小波分析的两个主要研究内容包括阈值和阈值函数的选取进行改进，为下一步损伤信号特征值提取打下基础。

1)阈值的选取：1995年，Donoho等人通过理论验证了最优的通用阈值。但在小波变换过程中噪声信号的小波变换系数幅值随尺度的增加而减少，信号的小波变换系数幅值随尺度的增加不会减少[3]。基于以上考虑，本文使用基于Birge-Massart策略的小波系数选择规则获取阈值。Birge-Massart策略中存在α的经验系数，为达到最优效果，采取粒子群算法寻找最优解。

2)阈值函数的选取：常用的阈值函数主要是软阈值和硬阈值函数，但都存在不足。硬阈值函数由于在门限阈值处不连续，所以重构信号会产生一些震荡。软阈值函数处理相对平滑，但会造成边缘模糊等失真现象[4，5]。本文在此基础上提出一种改进阈值算法，通过仿真实验数据表明，该算法能够减少损伤信号中的噪声并保留小奇异点。

1 小波阈值去噪

设有如下观测信号[6]：

f(k)=s(k)+n(k)

(1)

式中，s(k)为原始信号；n(k)为方差为σ2的高斯白噪声。

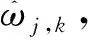
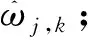
2 粒子群优化算法获取阈值

本文使用基于Birge-Massart策略的小波系数选择规则获取阈值λ，Birge-Massart策略是由j、α、M3个参数确定。给定一个分解层数j，对j+1层以及更高层，所有系数保留。对第i层(1≤i≤j)保留绝对值最大ni个系数[7]：

ni=M(j+2-i)α

(2)

式中，M和α为经验系数，规定α>1，缺省情况下M=L(1)。

通过粒子群算法寻找α的全局最优。粒子群初始化为一群随机粒子，然后通过迭代找到最优解，在每一次迭代中，粒子通过跟踪两个极值来更新自己，第一个是粒子本身所找到的最优解，称为个体极值pi，另一个极值是整个种群目前找到的最优解，称为全局极值pg。在找到这两个极值时，粒子根据如下的公式更新自己的速度vi和位置xi[8]。

vi=wvi+c1r1(pi-xi)+c2r2(pg-xi)

xi=xi+vii=1，2，3…N

(3)

式中，c1、c2为学习因子，r1、r2为[0，1]范围内的均匀随机数，w为惯性权重。

其具体过程如下：

1)初始化粒子群，包括群体规模N，每个粒子的位置xi和速度vi。

2)计算每个粒子的适应度值Fi。

3)对每个粒子，用它的适应度值Fi和个体极值pi比较，如果Fi>pi，则用Fi替换掉pi。

4)对每个粒子，用它的适应度值Fi和全局极值pg比较，如果Fi>pg，则用Fi替换掉pg。

5)更新粒子的速度vi和位置xi。

6)如果误差足够好或到达最大循环次数退出，否则重新计算每个粒子的适应度值Fi。

3 改进的小波阈值函数

常用的估计小波系数的方法有两种：硬阈值估计法和软阈值估计法。

3.1 硬阈值估计法

硬阈值估计法，其定义为[9]：

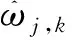
图1 硬阈值估计法

3.2 软阈值估计法

软阈值估计法，其定义为[10]：

图2 软阈值估计法

由于钢丝绳损伤信号的特殊性，既有由于多条断丝引起的大奇异点变化，也有由于少数断丝引起的小奇异点变化，如果用软阈值函数算法处理损伤信号，将只保留大的奇异点，如果用硬阈值函数算法处理损伤信号，将只消除小于阈值的小波系数，大于阈值的小波系数中同样存在噪声信号[11-19]。针对软硬阈值函数算法在检测矿用钢丝绳损伤信号时的缺陷，本文提出一种新的阈值函数：

式中，a∈(0，1) 。

当x>0时，

当x<0时，

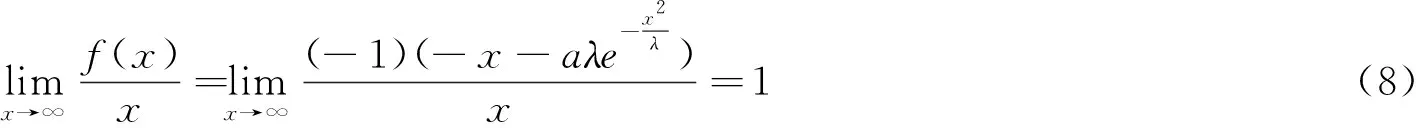
同时：

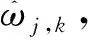
4 实验与分析

通过无损检测探伤仪采集的实验数据，采用sym5小波系，3层分解层数。基于粒子群算法的改进Birge-Massart策略获取阈值。首先在MATLAB R2016a软件平台编写关于求α最优解的粒子群算法，自定义c1、c2学习因子为1.2，w惯性权重为0.6，初始化群体个体数目为50。采取的适应度函数为信噪比函数，表达式如下：

式中，σ1为含噪信号的标准差；σ2为重构信号的标准差。

为了验证新阈值函数对矿用钢丝绳损伤信号的去噪效果，分别采取使用粒子群算法优化参数和不使用粒子群算法优化参数两种在软、硬阈值函数、文献[2]提出的阈值函数和本文的阈值函数下的重构后的损伤信号的信噪比进行对比。不同阈值函数对损伤信号去噪结果如图3所示，粒子群算法优化后的不同阈值函数对损伤信号去噪结果如图4所示。不使用粒子群算法优化参数时α取1.5。由结果表明当α=1.02时的阈值代入新的阈值函数重构出的损伤信号SNR能取得最大值。

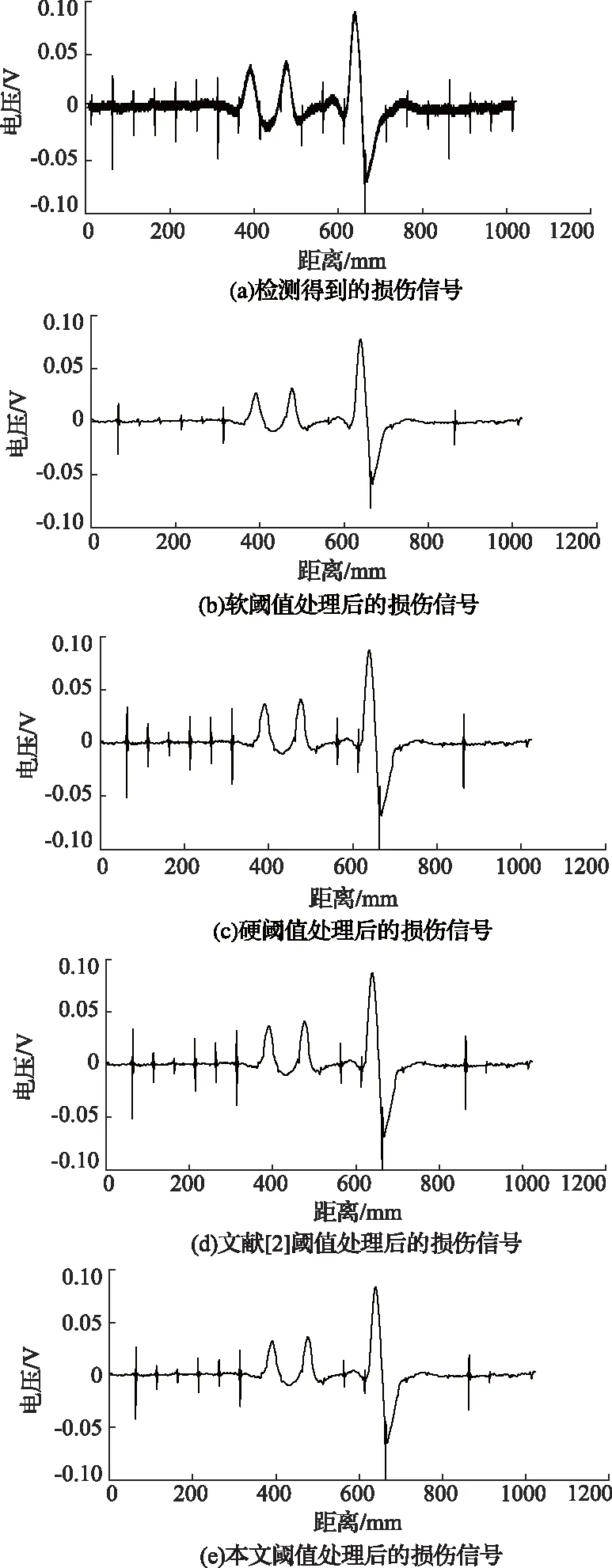
图3 不同阈值函数对损伤信号去噪结果

图4 粒子群算法优化后的不同阈值函数对损伤信号去噪结果

根据不同的去噪方法可以看出，软阈值函数去噪后虽然损伤信号平滑，但小的奇异点被一并去除，硬阈值函数虽然比软阈值函数保留了较多的小奇异点，但还保留了较多的噪声信号没能去除。不同阈值函数的信噪比对比见表1，通过表1可以看出，本文提出的阈值函数比文献[2]和硬阈值函数去噪效果好。但通过图3可以看出，对于损伤信号后半段的小奇异点保留的并不完整。

表1 不同阈值函数的信噪比对比

经过粒子群算法优化经验值α后，通过图4可以看出，不论是软、硬、文献[2]提出的阈值函数或者本文提出的阈值函数都得到了良好的改善。损伤信号后半段的小奇异点也基本保留。粒子群算法优化参数后的不同阈值函数的信噪比对比见表2，通过表2可以看出信噪比有明显的提升。经优化参数后获取阈值，并经过本文阈值函数处理重构的损伤信号能更多的保留原始信息。

表2 粒子群算法优化参数后的不同阈值函数的信噪比对比

5 结 论

1)本文提出的阈值函数比软、硬阈值以及文献[2]提出的阈值函数去噪效果好，但不能完整保留损伤信号中的小奇异点。

2)经粒子群算法优化经验值α后，重构信号能保留所有的小奇异点，再利用本文新的阈值函数得到的小波系数重构后，去噪效果比之前有所优化。