基于仿真实验的导轨结合面刚度建模方法研究

杜祯，刘博，白琳

（中国电子科技集团公司第三研究所，北京 100015）

引言

振动环境试验中常以扫频或模态试验的方式寻找设备各关键点的共振频率，但实验结果往往与仿真结果大相径庭，原因多为对仿真模型的处理方式不合理。

除材料、结构等因素外，设备的抗振性、静态特性、动态特性等性能受结合面力学特性影响较为明显。整机刚度作为一种衡量设备力学特征的重要因素，其约50 %受制于结合面刚度[1]，可见合理处理结合面关系对于模拟仿真结果的重要性。

本文以模态试验结果为参照值，用4种不同的结合面刚度数学模型进行计算仿真，并进行对比，以求寻找出最佳的等效刚度计算数学模型。

1 理论模型

本段主要基于分形理论和分形理论与域扩展因子两种建模方式分别对法向及切向动态接触刚度搭建理论模型[2]，经全排列组合后为后续进行仿真计算提供理论基础。

两种建模方式的区别在于，基于分形理论与域扩展因子的建模方式中，为使得实际接触面积值与粗糙表面真实接触面积之比能更加准确，引入了微观接触面积的接触点大小的分布函数的概念[3，4]。

1.1 基于分形理论的理论模型

1）法向

由分形理论基础，经量纲归一后，得法向接触刚度为：

式中：

D—近似为1.54/0.042Ra，其中Ra为粗糙表面粗糙度；

积；

2）切向

同法向，由分形理论基础，经量纲归一后，得切向接触刚度为：

式中：

μ—摩擦系数；

p—结合面法向总载荷；

Fτ—结合面总切向力。

1.2 基于分形理论与域扩展因子的理论模型

1）法向

基于微接触面截面面积的分布函数，对分形理论模型改进并经量纲归一后，可得法向接触刚度为：

2）切向

基于微接触面截面面积的分布函数，对分形理论模型改进并经量纲归一后，可得切向接触刚度为：

1.3 导轨结合面等效刚度模型

在导轨结合面中，重力起主要作用，这使得导轨结合面的处理相对简单，考虑到各方向刚度间的耦合关系，对其刚度计算过程加以改进，设每个接触面都有三个方向的刚度分别为Kx、Ky、Kz，法向刚度Knx、Kny、Knz，切向刚度Kτx、Kτy、Kτz，可建立如下模型：

2 建模、仿真与实验

依据上文建模方式，分别计算出导轨结合面的法、切向动态参数，以此建立有限元仿真模型。通过搭建实验台进行试验，优选误差最小的导轨结合面动态参数计算方式。

2.1 仿真实验台

为使影响因素相对单一，规避多结合面相互作用的影响，本文设计并搭建了一种模型结构如图1所示仅包含导轨结合面的实验模型。

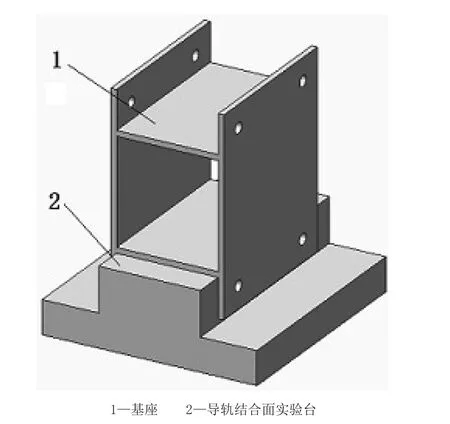
图1 导轨结合面实验台仿真模型

如图1所示，基座1模拟导轨滑块，导轨结合面实验台2模拟导轨。其中，基座与导轨结合面实验台可实现前后两方向上的水平移动。为使得导轨结合面特征更加显著，避免加工误差对导轨安装的影响及导轨与地面固定间结合面对实验结果的影响， 实验台设计时采用了导轨与基座一体式的倒T型结构。

2.2 参数计算

本文采用弹簧法进行结合面刚度分配，通过组成一个只有弹簧的柔性系统进行计算 。相关计算如下。

已知，试验台主体结构材料45#钢，其体积V=3 053.348 cm3；复合弹性模量E=1.13×1011N/m2；较软材料屈服强度σy=700 MPa；较软材料布氏硬度H=200 HB；名义接触面积Aa= 52 200 mm2；表面分型维数D=1.47；真实接触面积Ar= 22 446 mm2；临界接触面积ac=139.12 mm2。

利用前文的动态参数提取方法计算方法，按式（1）～（5）式计算可获得导轨结合面的动态接触刚度如表1所示。

2.3 导轨结合面仿真模型模态分析与实验

现将两种计算所得的法向及切向刚度计算值全排列组合，获得四种仿真方案，方案1中法切及切向计算方法均采用分形理论，量纲法向接触刚度及量纲切向刚度分别为6.71×109N/mm及3.58×1010N/mm；方案2中法向计算方法采用分形理论，切向计算方法采用分形理论与域扩展因子，量纲法向接触刚度及量纲切向刚度分别为 6.71×109N/mm及 4.33×109N/mm；方案 3中法向计算方法采用分形理论与域扩展因子，切向计算方法采用分形理论，量纲法向接触刚度及量纲切向刚度分别为4.22×108N/mm及3.58×1010N/mm；方案4中法切及切向计算方法均采用分形理论与域扩展因子，量纲法向接触刚度及量纲切向刚度分别为4.22×108N/mm及4.33×109N/mm。

以上述四种方案为依据进行模态分析，各方案所得模态振型相同，差异仅表现在固有频率中。由此，以一号方案为研究对象对其第一至第四阶振型进行研究，其对应各阶振型如图2所示。

第一阶振型为两侧面上段左右弯曲；第二阶两侧面两节点反向弯曲；第三阶两侧面两节点同向弯曲；第四阶两侧面各六节点反向弯曲。

以模型的基本外型为基础，酌量测点分布密度及位置，进行合理分割后，如图3所示创建一个由60个点组成的点线面共存的测试分析模型，三个方向合计测点数量为80个。由预实验结果及响应曲线，选取8号测量点作为激振点。

导轨结合面模型摸态测试实验前四阶振型结果如图4所示。

由图2与图4的对比结果基本一致可证明实验结果的有效性。依此，将四种方案中的计算数据代入仿真模型进行分析后，将其结果与模态测试的固有频率进行统计。

表1 计算结果

实验结果前四阶固有频率分别为153.91 Hz、543.43 Hz、889.85 Hz、1028.3 Hz；采用结合面绑定法仿真前四阶固有频率分别为178.81 Hz、700.11 Hz、1040.30 Hz、1056.20 Hz，其与实验结果间的误差分别为16.18 %、28.83 %、16.91 %、2.71 %；采用方案1进行仿真前四阶固有频率分别为155.87 Hz、604.75 Hz、937.74 Hz、970.74 Hz，其与实验结果间的误差分别为1.27 %、11.28 %、5.38 %、5.60 %；采用方案2进行仿真前四阶固有频率分别为155.87 Hz、604.74 Hz、937.74 Hz、970.68 Hz，其与实验结果间的误差分别为1.27 %、11.28 %、5.38 %、5.60 %；采用方案3进行仿真前四阶固有频率分别为155.41 Hz、604.32 Hz、937.50 Hz、950.05 Hz，其与实验结果间的误差分别为0.98 %、11.21 %、5.35 %、7.61 %；采用方案5进行仿真前四阶固有频率分别为155.41 Hz、604.31 Hz、937.47 Hz、949.94 Hz，其与实验结果间的误差分别为0.98 %、11.20 %、5.35 %、7.62 %。

为便于观察，以图表的方式比对各方案仿真与实际实验结果间的相对误差大小，详见图5所示。

图2 导轨结合面仿真模型有限元摸态分析前四阶振型

通过对比结果与图5可见，相对误差中，前四阶固有频率误差最小的方案依次为：方案4和3、方案4和3、方案4和3、方案1和2、方案1和2、方案1和2。虽然前三阶的误差最小为方案4和3，但其与方案1和2的差距很小可以忽略。故最佳方案应该在方案1和2之间选择。再考虑到两者切向结合面的刚度差值大小，根据实际的需求，刚度差过大会导致制造成本增加，在满足设计要求时应该选择刚度差相对较小的方案。因此，方案2的仿真方式综合相对误差最小。即结合面法向刚度采用基于分形理论的法向动态接触刚度理论模型，切向刚度采用基于分形理论与域扩展因子的切向动态接触刚度理论模型。故导轨结合面的最优处理方案为方案2。

图3 测试布点图及激振点

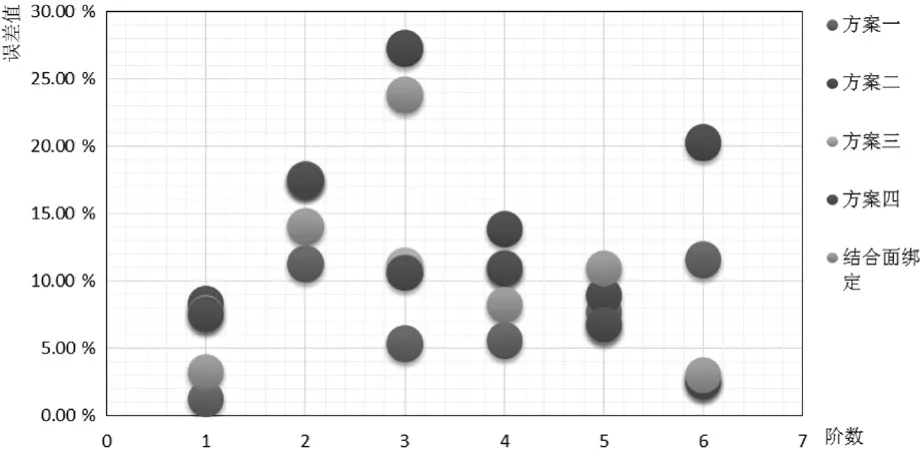
图5 各方案仿真结果与实验结果间的误差

3 结束语

本文主要以导轨结合面为研究对象，分析了其等效刚度的不同计算方法。对不同的方法进行了模态分析并与实际实验结果进行对比。结果表明：导轨结合面的刚度最佳计算方法为法向采用基于分形理论的动态接触刚度理论模型进行计算，切向基于分形理论与域扩展因子的动态接触刚度理论模型进行计算。