基于GIS和支持向量机模型的邯郸市降雨量空间分布研究

王 蕊

（河北省石家庄水文水资源勘测局，石家庄 050051）

基于地面离散而有限的站点观测资料精确反演一定区域上降雨分布，对精准模拟地表水文过程和水资源规划管理具有重要意义。当前学者们主要提出了基于地统计学 （Kriging、加权Kriging、混合Kriging）、样条函数、神经网络等方法。其中ANUSPLIN方法是面向气象要素的专业插值方法，其采用局部薄盘光滑样条函数并允许引入协变量，成为被IPCC推崇的数据处理技术之一［1-2］。然而多种方法适用性不同。例如地统计学方法较好解决了局部自相关问题，然而欠缺拟合逼近能力；ANUSPLIN等样条函数对数据时间分辨率及其分布要求严格；这为基于小样本的降雨空间模拟带来挑战［3-4］。相对而言，神经网络方法并不标定数据特征，也能够扩展协变量维数，因而具有较高的自由性。SVM是基于神经网络发展起来的数据分类方法，拥有神经网络的无限逼近的优点，同时能避免过拟合，能自适应拟合变量之间非线性关系［5］。本研究拟采用SVM方法构建邯郸市年均降水量空间分布模型，以期为区域降水量栅格化处理提供参考依据。

1 支持向量机回归原理

支持向量机（Support Vector Machine，简称SVM）是由基于统计学习理论的一种机器学习方法，利用核函数将非线性问题映射成高维空间中的线性问题，以最大超平面间距离准确分离不同类别向量。相比于BP、ANN等神经网络算法，SVM建立于结构风险最小原理基础上，能够较好规避小样本、非线性、高维数和局部极小点等问题。对于样本数据［xi，yi］，其中i=1，2， …，n，n为样本数据总数，xi∈Rn为样本输入，yi∈R为样本输出期望值。SVM的回归函数描述如式（1）：

对优化目标函数求极值，如式（2）：

式中 C为惩罚系数；Remp（f）为损失函数，设定ε不敏感函数为损失函数，则ε定义如式（3）：

其中，|f（xi）-yi|＞ε

引入松弛变量ξi和ξ*i，预测问题即转化为解决如下约束优化问题：

运用拉格朗日理论，由R（ω）的最小化解ai，a*i，得到用数据点表示的ω，如式（4）：

将式（4）带入SVM回归方程，即可得到相关样本输出值，如式（5）：

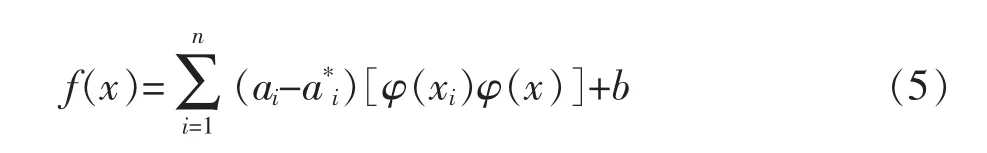
由于SVM理论只考虑高维特征空间的点积运算K（xi，x）=φ（xi）·φ（x），不直接使用映射函数，所以式（5）表达为：

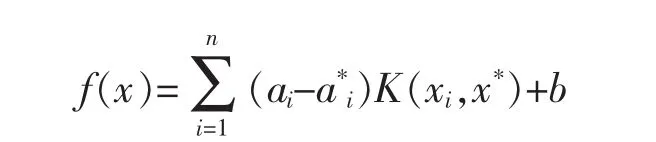
式中 K（xi，x*）为核函数。常用的核函数有：线性核函数（SVM-L）、高斯核函数（SVM-G）和Sigmoid核函数（SVM-S）等［4-6］。

2 研究区与数据处理

2.1 研究区概况

邯郸市地处冀南、太行山东麓，区域面积1.2066万km2。自西向东依次是太行山地、黄土台地、黄淮平原，高程介于0～1998.7m。区域属暖温带大陆性季风气候半湿润区，物候交替显著，年平均气温13.5℃，全年无霜期200d，日照时长2557h。该市主要有沁河、漳河，水流平缓、径流小。

2.2 数据来源与处理

邯郸市内有16个长期观测气象站如图1。本研究从气象数据共享服务网站上申请了1980～2010年各站点逐年统计资料。年观测数据无缺损，以近31年数据的平均值为该站点的年降雨量。DEM数据来源于地理空间数据云，其空间分辨率30m，投影系统WGS-84。区域行政边界矢量数据来自中国科学院资源环境数据中心，其比例尺1∶500mm。运用ArcGIS软件，以DEM数据为基础，提取邯郸市30m像素水平上的DEM、坡度、坡向等因子，再利用Raster to point工具将其转换为空间点特征，运用几何计算工具提取各点的经纬度信息。以各站点年均降雨量为目标变量，以DEM、坡度、坡向、经度、纬度为协变量，运用Rstudio软件对各变量进行描述统计分析，e1071包建立降雨量与环境变量之间的非线性隐含关系。ArcGIS10.5进行空间制图。

图1 研究区位置与气象站点

3 结果分析

3.1 降雨量与环境变量统计特征

表1为研究区16个气象站点年均降雨量及环境变量描述统计特征。可知，站点资料显示区域降雨量介于502.2～559.4mm之间，站点平均值为526.3mm，标准差为16.83mm，变异系数为3.19%。由于样本较少，Kolmogorov-Smirnov检验显示其并未通过5%水平信度检验，因而采用均方根转换后进行后续建模。在区域水平上，邯郸市DEM介于0～1687mm之间，平均DEM213.8mm，在30mm像素水平上的变异系数达2.35，呈现强变异。区域坡度范围为0～73.2°，平均值5.26°，变异系数达1.26。 坡向值域0～360，平均水平164.8，呈现中等程度变异（0.64）。K-S检验表明，反映地形的DEM、坡度、坡向变量和表示地理位置的经度、纬度变量，在30m像素水平上均符合正太分布特征。

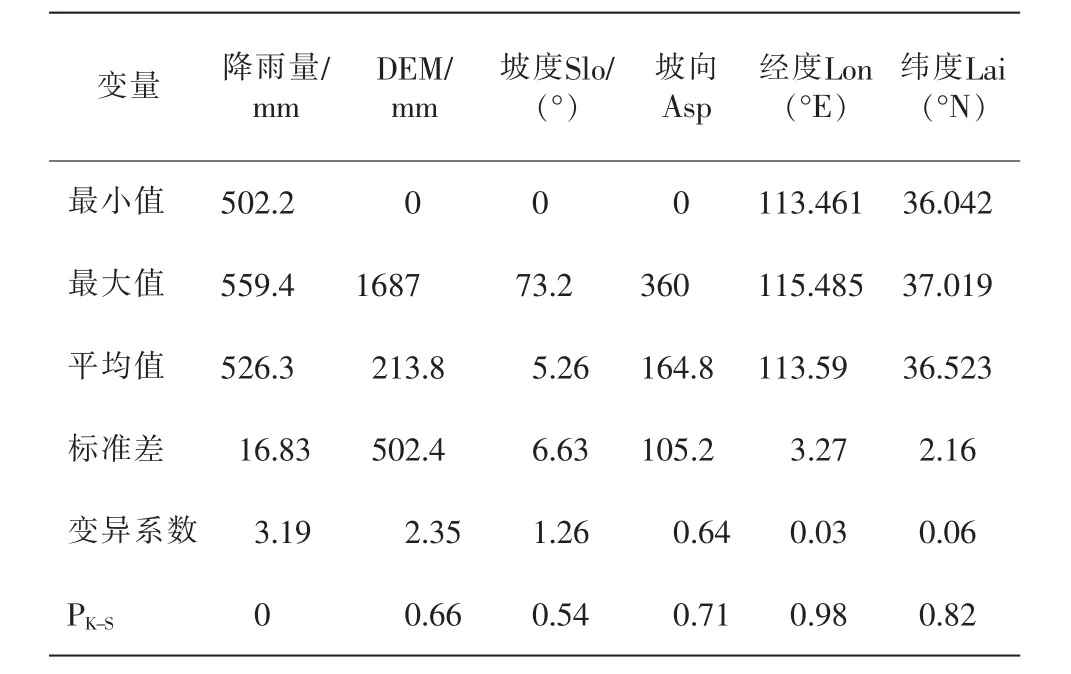
表1 降雨及环境协变量描述性统计特征

3.2 降雨量与环境变量相关性分析

环境协变量的分布特征深刻影响着模拟降雨的空间变异性。Pearson相关性分析能直观判别降雨量与环境因素之间的关系，从而更好认识降雨的地带性特征。如表2所示，降雨量与DEM呈现正相关关系，相关系数0.158，但并不显著。与坡度、坡向、经度、纬度呈现负相关关系，相关系数依次为-0.078，-0.214，-0.054，-0.07，也并未通过5%水平显著性检验。说明区域降雨量与环境因子的关系并不明显，但并不意味着降雨对这些环境因素无依赖性。主要由于该矩阵反映了全局空间离散关系，而降雨是区域性变量，可能在局部空间具有强烈变异，从而削弱了环境因子全局空间关系。

表2 降雨与环境协变量相关性矩阵

3.3 邯郸市降雨量空间分布

通过设置不同的核函数对邯郸市年均降雨量进行空间分布模拟，得到结果如图2。

图2 研究区降雨量空间分布

由图2可知，不同建模方案模拟的降雨量具有一致性的全局特征。例如，降雨呈现环状聚集分布，峰峰矿区、磁县、曲周和鸡泽等地形成了降雨低值中心，大名等为次低中心；邯郸县、馆陶等地为高值中心。然而降雨分布细节信息存在一定差异。例如，线性核函数（SVM-L）得到的降雨量分布图具有更明显的空间平衡，值域介于489.3～567.2mm。高斯（SVML）、S（SVM-S）核函数体现了局部离散信息，其值域分别为500.5～565.3mm，499.8～558.9mm。3种方法模拟的降雨平均值介于523.1～523.8mm，相差甚小，空间变异系数为22.04%，这与表1显示的结果一致。

3.4 邯郸市降雨量模型评价

由于站点分布离散、有限，因此采用留一交叉验证（迭代运行16次，每次运算过程中以其中一个测站的年均降雨量为验证）对上述3种模型进行综合评价，如图3。

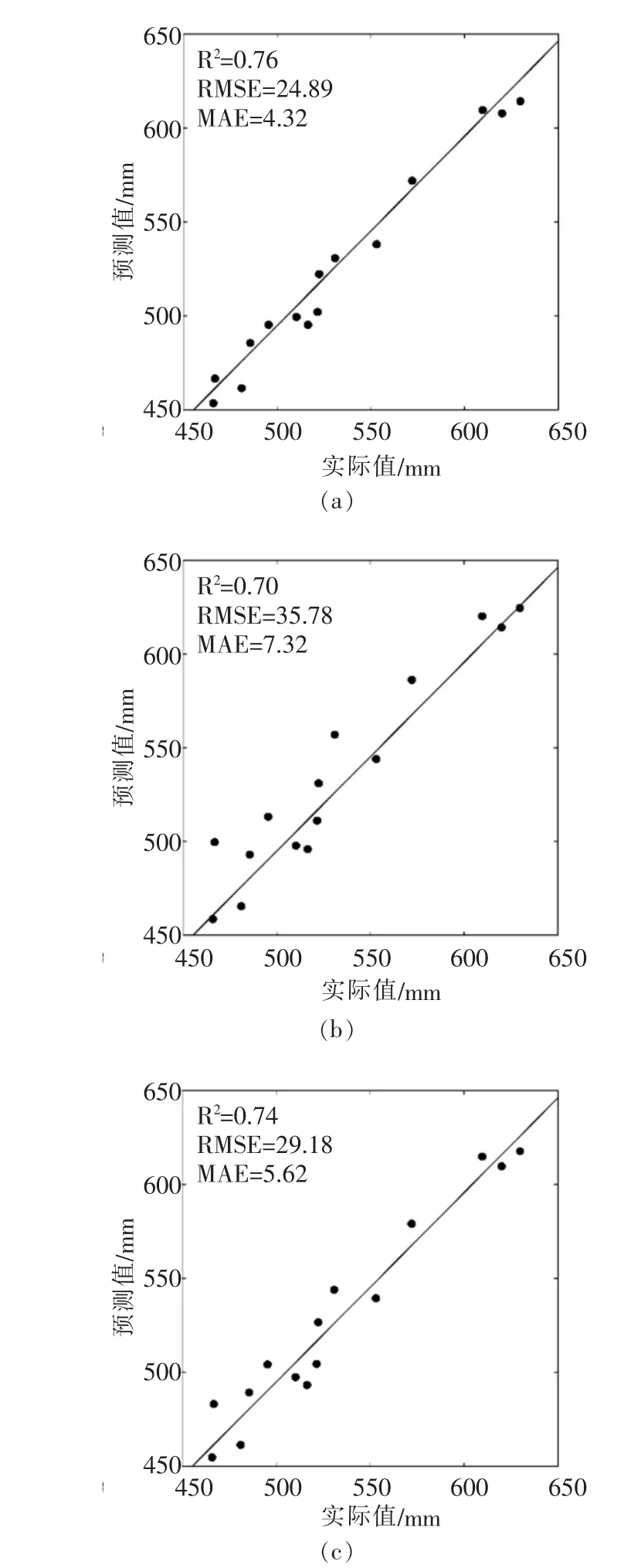
图3 各气象站点年均降雨量实际值与预测值

结果表明，线性核函数模型 （a）的R2最高，达0.76，RMSE和MAE均最小，为24.89，4.32mm。 高斯核函数（b）模型的R2最小，仅为0.70，相应地RMSE和MAE均最大，为35.78，7.32mm。 S核函数（c）模型的R2为0.74， RMSE、MAE分别为29.18，5.62mm。 由此来看，线性核函数的拟合能力最佳，适用于区域降雨量空间分布建模。

4 结语

本研究基于有限的地面观测资料结合DEM、经纬度等空间数据，运用支持向量机回归模型构建了线性核函数 （SVM-L）、高斯核函数 （SVM-G）和Sigmoid核函数（SVM-S）等3种降雨量预测模型。相关分析表明，降雨量与环境因子不存在显著的全局关系，可能在局部存在非线性平稳性。3种模型中，线性核函数（SVM-L）表现最佳，模型R2相对于（SVM-G）、（SVM-S） 提 高 了 0.06，0.02，RMSE 减 小 了 10.89，4.29mm，MAE降低了3，1.3mm。SVM模型不仅能克服全局非线性影响，还能通过丰富的协变量信息反映降雨局部分布特征，拟合结果与站点实测值吻合。