基于Copula理论承德市降水与温度相关性量化研究
郭家骥
(河北省承德水文水资源勘测局,河北 承德 067000)
对于降水和温度的相关性,虽然已有部分研究成果,但研究思路多为:首先将两者独立分开研究,然后基于某种线性理论的方法将两者进行结合[1-3]。目前, 衡量变量间相关性多采用Pearson系数ρx,y、Kendall秩相关系数τ和Spearman秩相关系数ρs此3类系数。这些方法在一定程度上虽然能表述两者的相关性,但其要求随机变量的方差要保持在某些特定的区间之内,且方法本身也只适用于表示两个变量之间的线性关系或单调关系,对于变量降水和温度这类时常会发生非线性增减变化情况,线性理论相关方法显得捉襟见肘。
针对上述方法存在的不足,研究重新梳理了思路,引入在表述多变量关联性领域具有独特优势的Copula函数理论,用于研究降水和温度的相关性和两者之间的联合特性,探究最合适的表述降水和温度关系的Copula函数类型,从而实现精确量化两者相关性的效果。
1 研究方法
1.1 常用相关性系数
Pearson系数、Kendall系数和Spearman系数是目前描述两变量 (如降水与温度)相关性最主要的方法。Pearson旨在反映变量间的线性关系;Kendall系数(也作和谐系数),通常用τ表示,是一种通过研究随机变量等级而反映相关程度的方法,此法需要提前对变量进行定类分析;Spearman系数通常用ρs表示,它是对两变量的秩进行线性相关研究,且不限制其各自分布情况,但统计效率相比Pearson稍差。3个相关性系数的表示式为:

式中 X,Y为变量;E(·)为期望;n是样本容量;sgn为阶跃函数;rgX和rgY分别为随机变量X,Y的秩;cov (·)为协方差;σ为标准差。
1.2 Copula函数与相关性
“Copula”源自拉丁文中的“连结”一词,其用于定量表达多维联合分布与对应边缘分布的相关关系。Copula函数可有效地构建联合分布函数,构建的形式为:任意的m维联合分布函数可拆解成1个Copula函数和m个边缘分布的形式,Copula函数为连接边缘和联合分布的桥梁[4-5]。形式为:

式中 Fm(xm)和H(x1,x2,…,xm)分别为边缘分布与其对应的联合分布;C为连接形式或规则。
降水和温度作为水文循环中的重要因素,降水的增减可以在一定程度上影响区域的温度变化,而区域温度的升降则会影响水文循环中的蒸发速率,进而对降水产生反馈作用。两者互相影响和联系,故而引入Copula函数理论来量化研究降水与温度的相关性。若分别以F(x)和G(y)表示降水和温度的分布函数,则应有两维Copula函数C(u,v),使得等式H(x,y)=C[F(x),G(y)]成立。
1.3 Copula函数选取
在水利科学研究中,Copula函数可分为Elliptical Copula(椭圆族)和Archimedean Copula(阿基米德族)两类。其中,Elliptical Copula(椭圆族)主要有Normal Copula和t-Copula函数2种;而对于Archimedean Copula(阿基米德族),主要有Clayton Copula函数、Frank Copula函数及Gumbel Copula函数3种。针对本文研究的降水和温度的二维形式而言,上述5种Copula函数的表达式为式(5)~式(9),各个函数的密度函数及具体内容详见参考文献[6]:
(1)Normal Copula函数

式中 u,v分别为边缘分布;θ为需估计的参数。
1.4 Copula函数拟合度测验
拟合度是衡量Copula函数的匹配效果的。若理论分布和经验越相近,则拟合效果越好,该指标可以有效地反映选择的理论分布质量的好坏。研究中通过拟合度测验对一系列待选Copula函数进行优选,从而选出最优者。检验拟合度优劣的方法主要分为相关性测度法和AIC值和OLS值最小准则法。对于Copula函数中相关性测度法的详细内容,具体可结合文献[7],此处不再赘述;而对于AIC和OLS值最小准则法,有:

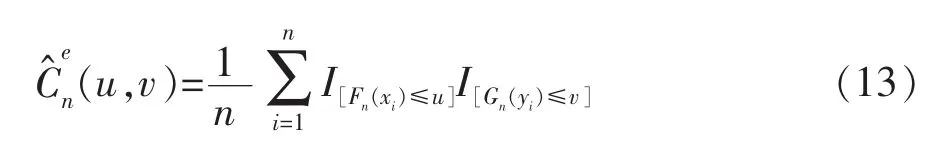
式中 I[·]为示性函数,当Fn(xi)≤u时,I[Fn(xi)≤u]=1,否则I[Fn(xi)≤u]=0;MSE为平均误差;m为参数数量;n为样本容量。AIC值通常小于零,AIC值和OLS值最小时,则拟合度最优。
1.5 参数估计
非参数法、全参数法和半参数法是进行Copula函数的参数估计的主要方法。其中,对于非参数法,Copula联合分布函数的参数几乎完全决定于两个边缘随机变量之间的相关性关系 (通常是秩相关系数);全参数法中极大似然法(MLE)和分布推导法(IMF)使用最为广泛,但前者需要提前对各个边缘分布中参数进行估算确定,进而才可估计联合分布的参数,且此方法计算过程过于繁冗;后者需要提前拟定两个边缘分布的函数类型,而边缘分布类型的确定本身就存在较大的主观性,或许不能客观科学地反应边缘分布的真实情况。因此,本研究采用兼顾两者优点的半参数法。
对于半参数法,可以使用经验分布函数Fn(xi)和Gn(yi)来代替边缘分布函数F(x,θ1)和G(y,θ2),从而避免边缘分布的参数估计,如此可直接估计联合分布的参数,表达式为:

半参数法中,似然函数并不需要确定边缘分布是属于何种分布类型,因此其并不会受到边缘分布类型的限制,变量间的联合分布多取决于变量间的关系,而和其各自的边缘分布并没有关系,且此方法计算比较高效快捷。
2 基于Copula理论的降水与温度相关性研究
2.1 年降水与温度的相关性
2.1.1 计算边缘分布函数
首先,对于承德市1978~2017年共40年的长系列降水与温度数据进行整理分析。在计算边缘分布时,本此研究中采用基于经验分布函数和高斯核函数理论相结合的方法,以样本经验分布函数近似当作总体分布函数进行计算,方法具体内容可参见文献[8]。首先,将降水和温度样本分别进行归一化处理;然后对其归一化值的累积概率F(x)进行统计计算,并以归一化值和其对应的累积概率描绘散点;之后,利用高斯核函数确定降水和温度的边缘分布,如图2。
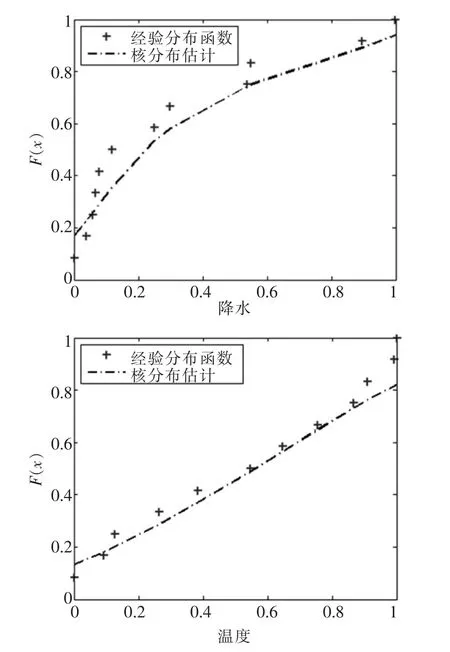
图2 承德市年降水与温度边缘分布
2.1.2 计算相关性系数
根据年降水和温度资料,采用常规方法计算3大相关性系数:Pearson、Kendall系数和Spearman系数,将计算结果列于表1中。

表1 年降水与温度3大相关性系数值
2.1.3 Copula函数初选
根据年降水和温度数据,以相关性测度法计算5种待选Copula函数对应的Kendall系数和Spearman系数,并与表1进行比较。初选出两种较优的Copula函数用于下一步优选。
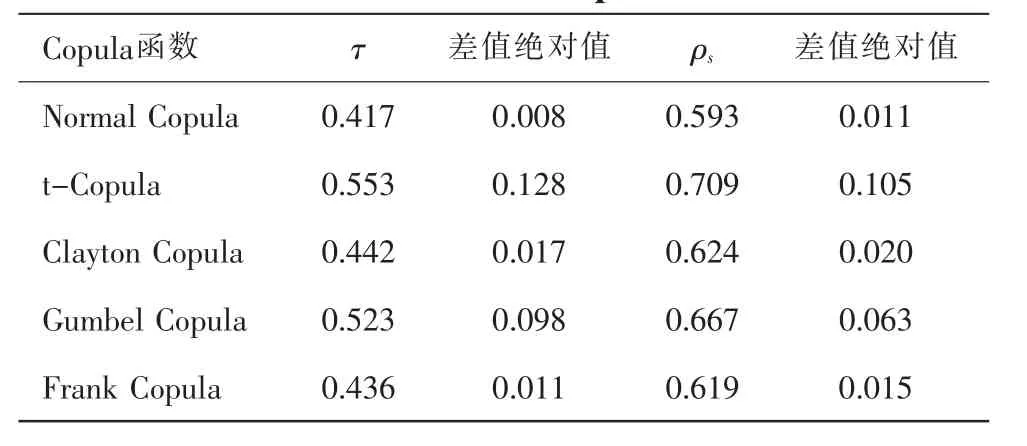
表2 年尺度降水和温度的不同Copula函数相关性测度值
通过表1和表2比较分析可得出,Normal Copula函数和Frank Copula函数对应的Kendall系数τ与Spearman系数ρs与表1中相应值最相近。
2.1.4 参数估计与函数优选
采用半参数估计法对Normal Copula函数与Frank Copula函数中的参数进行估算。然后,以经验联合分布和上述估算好参数的两个函数为基础,根据式(10)~式(13),分别计算两种情况下的AIC值和OLS值,将结果列于表3。
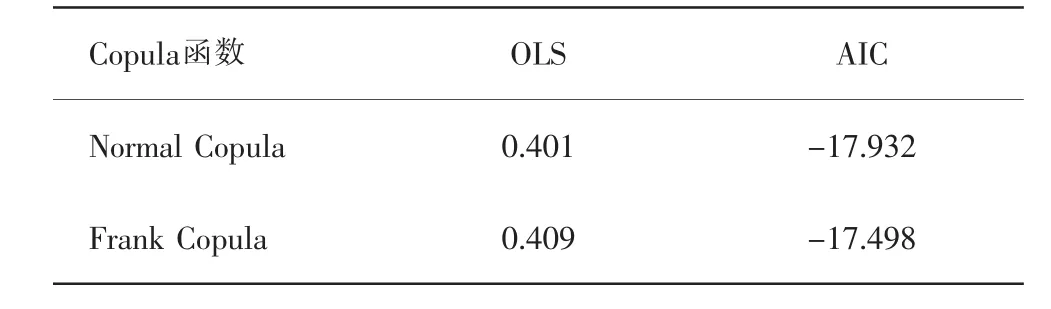
表3 承德市年降水与温度拟合度评判值
由表3可知,Normal Copula函数对应的AIC值和OLS值较小,分别是0.401和-17.932。由此表明,对于年尺度上,Normal Copula函数在表述降水和温度相关性时拟合效果最优。
通过优选可知,Normal Copula为表征降水和温度相关性最好的Copula函数。之后,通过Matlab编程计算,用Normal Copula函数可绘出降水和温度的联合概率密度和联合分布函数图像,图中的边缘变量降水和温度的相关函数分别以u和v表示,如图3。

图3 年降水和温度Normal Copula
从概率密度分布函数与联合分布函数图像可知,降水和温度存在一定的相关性。结合计算的三大相关性系数可知,两者的线性相关系数为0.471,Kendall为0.425,Spearman系数为0.604, 属于中等相关。并且通过优选可知,相比其他4种Copula而言,Normal Copula函数可以更好地定量描述两者之间的联合分布,通过Normal Copula联合分布函数,可以探究不同频率的降水和温度之间的联合重现期,进而研究不同频率下,同时考虑降水和温度因素的降水和温度的联合水文事件。
2.2 季节性降水与温度的相关性
为了进一步探究季节性降水与温度的相关性,研究在季节性尺度上,是否依然是Normal Copula函数在描述两者关系时表现最优。同样地,按照年尺度研究方法,以降水与温度数据为基础,分别计算春、夏、秋、冬4个季节的Pearson系数、Kendall系数和Spearman系数。首先,确定4个季节的降水和温度的相关性,然后针对相关季节,按照计算流程进行研究,寻找各季节最佳Copula函数。

表4 4个季节降水与温度3大相关性系数
由表4可知,春、夏、秋、冬4个季节的相关性系数中,只有夏、冬两季的3个相关性系数均大于0.4,春、秋两季对应的3个相关性系数则都不超过0.15。因此,夏季和冬季的降水和温度存在相关性。分析原因,可能与承德市的降水季节性分配有关系,对于夏季,承德市6~8月的降水量超过全年降水总量的65%。而冬季的降水仅占约15%,且承德处于温带季风带,冬季寒冷干燥,干燥的空气反而不利于土壤和植被保持水分,水分更容易因蒸散发而流失,从而影响降水结构和过程的变化。因此,在降水较少的冬季,降水和温度反而变得相关。
根据计算流程,同样采用基于经验分布函数结合高斯核函数方法求得承德市夏季和冬季的降水和温度的边缘分布,如图4。

图4 夏季和冬季降水与温度的边缘分布
从季节性降水与温度经验分布和高斯核分布图可知,夏季和冬季的降水和温度在经验分布上存在较小差异。采用相关性测度法分别计算承德市夏季和冬季降水和温度的5种Copula函数对应的Kendall和Spearman系数并与表4对比,进行初选。

表5 夏、冬两季降水和温度的相关性测度值
通过初选可看出,与年尺度一样,同样为Normal Copula和Frank Copula 2个函数的值和与表4中的值最接近。因此,初步选取Normal Copula和Frank Copula函数为优选对象。之后,采用半参数估计Normal Copula和Frank Copula函数中的参数,然后将2个理论Copula函数与经验Copula函数进行比较计算,以AIC值和OLS值最小为评判依据,进而优选出最合适的Copula函数,计算结果如表6。

表6 夏季和冬季的降水与温度拟合度评判值
通过计算和比较两个函数的OLS和AIC值可得,不论是冬季还是夏季,虽然两个函数计算结果相差不大,但Frank Copula函数较Normal Copula函数OLS和AIC值稍小,夏季是0.22和-118.932,冬季是0.18和-132.401。因此,Frank Copula在表述季节性尺度上的降水和温度相关性具有优势,它是刻画季节性降水和温度相关性的最优Copula函数。以Frank Copula理论为基础,编程绘出承德市夏季和冬季降水与温度的概率密度分布函数和联合分布函数图像,图中的边缘变量降水和温度的相关函数分别以u和v表示,如图5。

图5 夏季和冬季的Frank Copula联合概率密度和分布函数
由概率密度函数和联合分布函数图像可知,夏季和冬季两个季节的降水和温度的相关性存在较小差异,联合概率密度函数的值域范围不同。表明在季节性尺度上,降水和温度的相关性呈现类似规律,通过研究联合分布函数及其特性,可为更好地研究降水和温度的相关关系和季节尺度上的不同频率和联合分布提供参考。
3 结语
(1)在年尺度上,承德市降水和温度表现出中等相关的特征,在表述两者相关性上,Normal Copula函数表现最优;在季节性尺度上,仅夏季和冬季降水和温度相关性明显,在表述相关性上,Frank Copula函数表现最优。由此可知,在表征降水和温度相关性方面,Normal Copula函数在长时间尺度(年)最具优势;而Frank Copula函数在短时间尺度(季)较为突出。
(2)年际降水和温度在一定程度上呈现出平均的特点,相关性不如季节性明显,在季节性降水和温度关系研究中,降水最多的夏季和降水最少的冬季相关性表现较为明显。
(3)降水和温度的相关性量化研究可为下一步研究不同频率、联合重现期情况下的水文事件和相关的自然灾害(如极端降水、极端干旱和极端高温)提供理论基础。

