热轧带钢三维温度计算与应用

徐 耀,沈际海

(宝山钢铁股份有限公司中央研究院,上海 201999)

温度是热连轧产线控制的基本要素,准确的温度才能为轧制力模型高精度计算、性能预报、终轧/卷取温度控制策略优化等模型创造条件。常规温度模型针对头部进行平均温度计算,未考虑带钢宽度方向温度分布,仅从厚度方向划分层别,使用一阶差分温度模型计算各层温度,取各层温度平均值用于热轧所有控制模型计算[1]。此平均温度在头部轧制力计算、终轧温度计算模型中基本满足需求,但单点的温度无法为全长轧制力、温度预测提供帮助,也无法为性能预报模型提供必要的横向温度数据。本文所述三维温度模型把带钢沿长度方向切分成众多截面,使用二维温度模型计算各截面温度分布后,通过插值补充更多截面,最后把长度方向所有截面进行串联,形成长宽厚三维温度场。在此基础上调整边部加热控制策略与机架间冷却水策略,使带钢整体温度更加均匀。

1 三维温度模型

三维温度模型是指从长宽厚三个维度计算带钢温度分布的温度模型,计算范围如图1,覆盖热轧出炉至精轧出口范围内的所有区域。模型以加热炉出炉温度为基础,假设烧钢温度均匀,同一截面温度相同,再充分考虑空冷、水冷、轧制变形升温完成精轧出口温度(FDT)计算,计算过程与轧线L2控制模型一致。

本文以二阶差分的方式计算带钢一个截面宽度、厚度方向温度分布,构建一个面的二维温度模型。三维温度模型根据轧线速度图与负荷分配动态计算各段空冷时间、水冷时间,并以二维温度模型为核心,分别计算长度方向上的所有截面经过空冷、水冷、形变后的温度,再把所有截面温度按空间顺序进行串联,模拟出长度方向的温度分布,实现长宽厚三个维度的温度场计算。

1.1 截面网格划分

在带钢截面厚度方向上划分网格,采用不固定层别步长的方式划分网格,层别划分方式如下:带钢厚度为h,网格数量设定为n,步长为Δhi,i=1,2,3…,n-1,n。

约束条件:

(1)

在带钢截面宽度方向上划分网格,同样采用不固定层别步长的方式划分网格,因板坯宽度相对较大,需要增加层别数量,以减小步长,更有利于热传导计算。层别划分方式如下:带钢宽度为w,网格数量设定为n,步长为Δwi,i=1,2,3…,n-1,n。

约束条件:

(2)

1.2 长度截面划分与空间映射

以板坯长度为基准,在长度方向上划分多个截面位置,因头尾空冷影响面积大,因此以小间距密集的方式部署,板坯中部适当放大距离。轧制是形变过程,需要根据各机架出口尺寸,计算板坯长度变化系数,实现截面位置在经过不同机架轧制后的空间映射:

Lz=Lz-1+ΔLz

(3)

式中:z为截面位置顺序号;Lz为截面位置顺序z距离板坯头部距离;Lz-1为截面位置顺序z前一个计算位置距离板坯头部距离;ΔLz为截面位置顺序z与前一个计算位置的距离间隔。

在空间上需要计算板坯同一位置在各机架轧制时的实际长度。因此,根据各机架预设定出口厚度,以板坯长度为基准计算板坯长度方向上不同位置在各机架轧制时所对应的实际轧制长度:

Ki=Si/Sslab

(4)

式中:i为机架号;Ki为机架i轧制长度与板坯长度的比例系数;Si为机架i的出口带钢截面面积;Sslab为板坯截面面积。

在空冷时间、水冷时间计算时,需要根据截面在板坯上的位置计算其在各温度计算点的轧制长度映射:

Liz=Ki·Lz

(5)

式中:Liz为机架号i截面位置z对应的出口实际长度。

1.3 截面温度计算

二维温度模型[2],是指把原点定位于带钢截面中心,从厚度与宽度两个维度分析温度分布情况,本温度模型利用二阶差分计算截面温度分布。在进行计算的区域内,设定带钢横截面厚度及宽度方向的网格点。利用二阶热传导差分方程公式(6)求解[3-4]:

(6)

本文以带钢截面左下角为原点,在厚度方向划分层别y,宽度方向划分层别x,采用显式差分进行计算。

内部节点使用公式(7)计算:

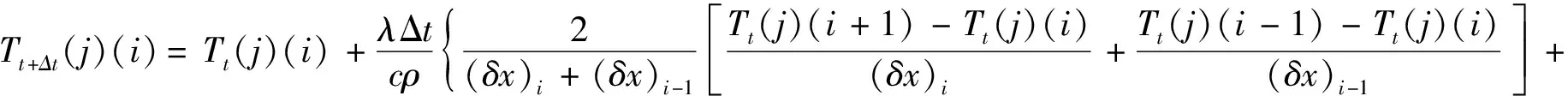
(7)

式中:Tt(j)(i)为板坯宽度方向网格i、厚度方向网格j在t时刻对应温度,℃;Δt为温度计算时的时间差;(δx)i为第(i,j)网格及第(i,j+1)网格的距离;(δy)j为第(j,i)网格及第(j+1,i)网格的距离;ρ为密度,kg/m3;c为比热容,J/(kg·K);λ为网格对应的热传导率,W/(m·K)。

使显式差分公式分别在板坯宽度方向(i轴方向)、板坯厚度方向(j轴方向)隐式化,采用两个方向隐式化公式交替使用的方式,解三对角矩阵计算温度:

F(t)=(T,radio,t)

(8)

式中:F(t)为二维温度计算函数;T为输入温度;radio为辐射系数,t为持续时间。

1.4 空冷温度计算

带钢的同位点在轧线上属于运动过程,实际形变时间短,多数暴露于空气中进行搬运。因此,根据轧机与水冷设备布局,如图2把同位点空冷划分为多个连续时间块。

以设备布局为基准,计算带钢同一位置在两个设备间的空冷时间。空冷时间包含轧制空冷与辊道搬运空冷两部分。轧制速度涉及加速、匀速、减速三种状态,使用公式(9)计算带钢在各机架单位长度轧制所需时间:

(9)

式中:t1为加速段持续时间;t2为匀速段持续时间;t3为减速段持续时间;L为轧制长度;t′为单位长度轧制所需时间。

空冷时间基于轧制时间计算公式(9),结合带钢长度方向位置,计算指定位置空冷时间:

tair=l·t′+troller

(10)

式中:tair为带钢指定位置空冷时间;l为带钢指定位置至带钢尾部距离;troller为带钢在辊道上非轧制状态时的搬运时间。

空冷温度计算是指在轧制工艺的基础上,结合时间区间划分(图3)使用公式(10)为每一个时间块计算其连续空冷时间。使用二维温度计算公式(8),根据环境温度计算带钢指定位置经过空冷后温度变化。

1.5 水冷温度计算

轧线水冷区域分为除鳞箱体冷却、机架前后除鳞冷却两类(如图3)。除鳞箱以箱体的形式,带钢同位点在其内部经过持续时间水冷,以除鳞箱长度结合速度图计算水冷时间;机架前后冷却水也覆盖一定长度范围,因此同位点在此冷却时间也按长度区间根据速度进行换算。

使用二维温度模型公式(8),根据冷却水水温计算带钢指定位置经过各水冷区间所需时间,计算带钢指定位置经过水冷区间后的温度变化[5]。

1.6 形变温度计算

轧制形变带来轧件温度改变,且带钢与轧辊接触存在传导热损失,综合二者后使用式(11)计算形变后的温度变化[6]:

Tnew=Told+ΔTdeform-ΔTcon

(11)

式中:Tnew为变形后温度;Told为变形前温度;ΔTdeform为变形温差;ΔTcon为轧件与轧辊的热传导温差。

形变温度变化不按宽度、厚度两个维度分层,按截面平均温度计算,温度差平均叠加到所有网格上。

1.7 电磁感应加热功率计算

部署在中间辊道上的板坯两侧的边部加热器(EH),采用电磁感应原理对板坯边部进行补温加热,通过如下加热器设定模型计算指定温度提升所需的功率:

P=F(h,w′,c,te,T,ΔTeh)

(12)

式中:P为设定功率;w′为带钢边部加热宽度;te为边部加热时间;ΔTeh为目标提升温度。

边部加热功能启用时,以边部温度为基准设定加热功率,加热设定模型中T与ΔTeh呈线性关系,因此加热后可以实现加热区域温度提升且加热区域温度均匀化。

1.8 三维温度场模拟计算

带钢以板坯为原型尺寸,按头部长度0.2 m、头部截面间距0.015 m、中部截面间距0.15 m、尾部长度0.2 m、尾部截面间距0.015 m划分所有截面,头尾温度变化幅度大,因此截面密度变大。在横截面上以等间距密集划分宽度方向、厚度方向网格(如图4)。

三维温度模型对带钢所有截面从出炉开始经过HSB除鳞、粗轧、中间辊道、FSB除鳞、精轧一系列温度计算后,以精轧出口测温点为终点,记录所有截面温度分布。

在长度方向以温度计算截面数值为基准,插值计算添加更多截面,细化截面间距,形成温度连续变化的带钢全长温度曲线。至此,带钢全程三维温度场温度数据计算完成。

1.9 三维温度应用

轧前根据带钢头部控制参数与速度图,使用三维温度模型计算未使用边部加热器时精轧出口带钢全长温度场、在未启用边部加热器时宽度方向描述边部温度差异(如图5)、启用边部加热器后宽度方向温度分布(如图6)以及在长度方向上描述温度变化趋势(如图7)。

由图5可知,带钢两侧有明显温度下降,宽度约占总宽度5%,温度梯度差约65 K。

边部加热器控制模型根据横向温度分布调整边部加热距离、加热功率,补偿边部温降,使精轧出口带钢宽度方向温度更趋向均匀(如图6)。

终轧温度前馈控制模型[6]根据全长温度变化(如图7),提前预设机架间冷却水流量,使带钢全长温度更加稳定。

2 应用效果

采用上述模型,选取样本钢种普碳钢AT3482D,板坯宽度为950 mm、厚度为230 mm、长度为10.4 m,抽钢温度为1 222 ℃,粗轧道次策略为3-3模式,精轧目标厚度为2.62 mm、宽度为785 mm、温度为860 ℃,计算样本带钢在精轧出口FDT处三维温度场。

精轧控制穿带速度策略:穿带速度为8.5 m/s、一加加速度为0.029 m/s2,二加加速度为0.1 m/s2,最大速度为15.5 m/s。

精轧机架间冷却水:初始开F2、F3两组机架后冷却水阀门开度分别为50%、25%。

三维温度模型网格划分:厚度均匀分为7层,宽度均匀分成15层。

长度截面分布:头部长度为0.2 m,头部截面间距为0.015 m;中部截面间距为0.15 m;尾部长度为0.2 m,尾部截面间距为0.015 m。

外围温度:环境温度为27 ℃,水温为28 ℃。

三维温度模型以全长轧制实绩(轧制功率、冷却水、轧制速度)为基础,计算并输出三维温度场,以截面平均温度描述全长温度曲线,与实绩FDT测温曲线对比,如图8所示,计算值与实际值基本一致,表明模型计算温度相对可靠。

带钢截面温度场描述截面温度分布,温度分布图(如图9)表明,厚度方向各层温度基本相同,宽度方向在边部3.5 cm左右存在约65 K温度快速下降。

启用边部加热器(EH),加热带钢两侧边部,加热宽度为25 mm,目标温度提升50 K,设定加热功率为3 015 kW,可以有效改善边部温度,使宽度方向温度分布更加均匀。

3 结论

(1) 把带钢截面按宽度、厚度划分网格,计算一个面的温度分布。在带钢长度方向上按一定间隔把带钢划分成数量密集的截面,形成长宽厚三个温度温度网格区域。分别计算各个截面温度分布,以插值的方式补充截面之间的温度值,完成带钢全长三维温度场模拟计算,并实现图形化展示。

(2) 实例结果表明,三维温度计算模型计算结果与实际值基本一致,在终轧温度前馈控制与边部加热器控制方面具备一定应用价值。