碳纳米管-石墨烯纳米带过渡连接处的力学稳定性与热传导性质研究

田 川， 张宏岗， 胡 松， 王 辉， 陈元正， 王红艳， 倪宇翔

(西南交通大学 物理科学与技术学院，成都 611700)

1引 言

随着科学的进步，社会的需求，以及微电子工业的快速发展，开发出具有良好导热性和电绝缘性能的材料成为了近年来相关领域面临的挑战之一. 电子设备和集成微纳米机电系统的尺寸进一步缩小是推动纳米科学研究和技术进步的主要动力. 随着纳米器件尺寸的减小，纳米器件的散热问题越发突出[1]. 因此，微纳米尺度的热传导对纳米器件的性能和稳定性起着至关重要的作用. 碳纳米管和石墨烯由于其优异的导热性能，在未来微纳米集成器件中具有极大的应用前景.

碳纳米管是一种强度大、电子结构特殊、稳定性高、导热性能极好的一维材料[2-5]. 由于碳纳米管具有很大的长径比，因而在沿其长度方向的热交换性能极佳. 因为其极高的热导率，通过掺杂碳纳米管也可以改善复合材料的热导率. 另一方面，随着二维碳材料石墨烯的机械剥落[6]，其独特的物理特性[7-11]激发了越来越多的对低维晶体的研究兴趣.

虽然单一的碳纳米管或者石墨烯纳米带具有很好的热输运性质，但是这两种材料在热传导方面表现出明显的各向异性，大大限制二者混合使用时的热输运性能. 有研究讨论了一维到二维这种连接交叉结构具有优良的导电性能[12-13]，本文基于此，探索一种由一维结构向二维结构转变的连接处的热输运性质[14]，该结构通过一个连接过渡系统[15-16]将碳纳米管和石墨烯纳米带连接起来. 由于CNT- GNR过渡系统的结构、稳定性和热学性能尚不清楚，严重制约了该体系的进一步应用. 因此，本文采用分子动力学模拟[17-20]，研究CNT- GNR过渡系统的可能结构及其对应的力学稳定性和热传导性质.

2计算模型与方法

由于过渡系统所对应的最大开角(θ)尚且未知，因此我们建立了大量不同开角下的结构模型，以确定能维持该结构力学稳定性的最大临界角度，并且探索随着角度的变化，其热输运性质的改变. 整个系统总长为60 nm，石墨烯带的厚度0.335 nm，碳纳米管管径为0.6893 nm. 结构模型如图1所示，θ为过渡结构边缘与石墨烯纳米带边界的夹角(本文称为开角)，L为过渡结构的长度，h为碳纳米管与石墨烯纳米带边界的相对距离.

本文使用的方法为非平衡态分子动力学模拟方法(NEMD).[17-20]选用AIREBO势[21]来描述C-C之间的相互作用，该势函数能准确模拟碳纳米管和石墨烯的传热性质[22-24]. 本工作中的所有计算均使用Lammps软件[25]，三个方向均采用周期性边界条件. NEMD方法可以通过使用傅里叶定律来计算系统沿y轴方向的热导率k(Ly)：

(1)

我们采用Langevin热浴方法[26]，沿y轴将CNT-GNR结构按长度平均分为二十组来进行温度统计，热源和冷源温度分别为Thot=340 K和Tcold=260 K. 当达到稳态时，通过热源与冷源之间的能量传递速率来计算出热通量Q：

(2)

其中S为垂直于输运方向的截面积. 在NEMD模拟中，选取时间步长为1 fs，温度设定为300 K，采用velocity-Verlet积分方法[27]. 首先在NVT系综下模拟800 ps，使得整个体系结构的温度达到300 K，接着在NVE下继续弛豫200 ps；然后对结构两端进行热裕，4 ns后待结构内产生稳定的温度梯度分布，继续模拟6 ns来采集温度与热流的数据.

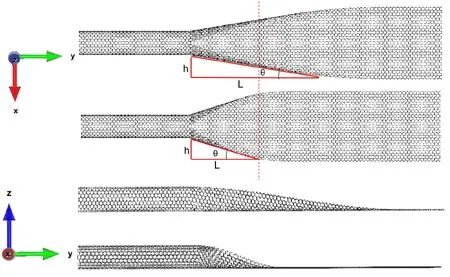
图1 碳纳米管-石墨烯纳米带过渡结构的模型. θ为过渡结构边缘与石墨烯纳米带边界的夹角(本文称为开角)，L为过渡结构的长度，h为碳纳米管与石墨烯纳米带边界的相对距离 Fig. 1 A model of the transition structure between carbon nanotubes and graphene nanoribbons. Theta is the angle between the edge of the transition structure and the boundary of the graphene nanoribbon (called the open angle in this paper), L is the length of the transition structure, and h is the relative distance between the carbon nanotubes and the boundary of the graphene nanoribbon.

3结果与分析

3.1最大开角的确定

我们从一个极大角和一个较小角分别逐次减小和增大角度进行夹逼,以此来找寻临界角度. 图2显示了在一个极大开角(21.3°)的情况下，开角远大于临界角，过渡结构中C-C键断裂，原子逸散，这样的结构显然不是一种稳定的过渡结构.

图2 非稳定结构Fig. 2 Illustration of an unstable structure

在接下来更加细致的找寻中，我们通过对每个结构进行NEMD模拟后的能量变化来判断其结构是否稳定. 在NEMD模拟中，我们输出了每个角度下的总能，势能和动能.

我们研究了四个角度，分别为6.7298°、8.4187°、11.227°、16.331°，从图三可知. 在前面三个角度下，逐次增大开角，其总能，势能和动能基本保持不变，当增加到16.3°时，结构的能量出现激增，这是由于C-C键断裂后，原子不断逸散，导致能量增大. 为了验证这个角度下的能量是否是突变的，即这个角是否为临界角，我们又计算了邻近16.3°的几个角(12.462°、13.442°、14.574°、15.216°、19.544°)所对应的能量. 从图4中我们可以看出，对于小于16.3°的角度，所有的能量都保持不变，能量只在开角大于16.3°的时候出现了突增，因此由能量大小的变化中我们得到了过渡系统开角临界值θ=16.3°.

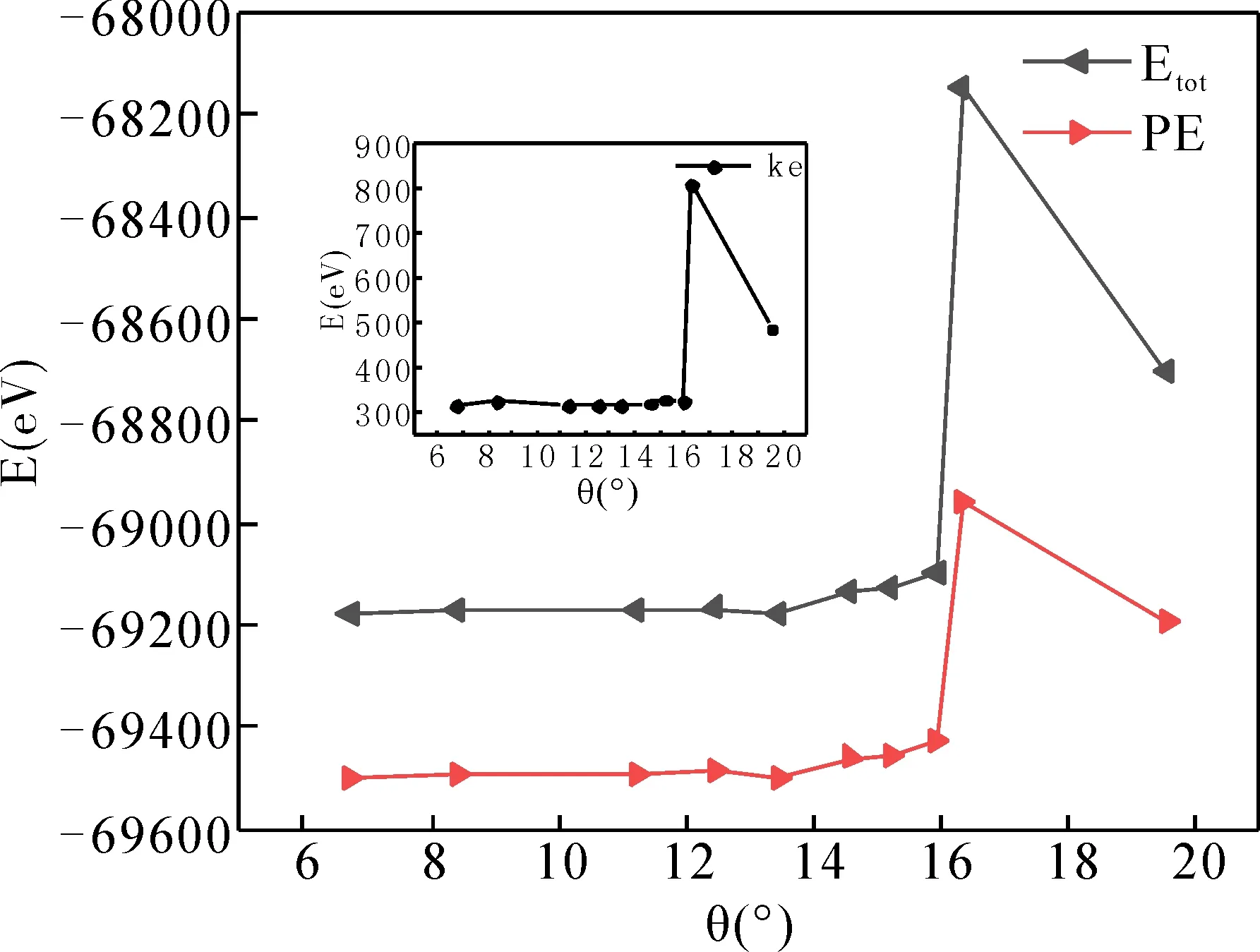
图4 不同开角下的能量变化Fig. 4 Energy versus the open angles

3.2临界角与临界长度

在以上的工作中我们确定了管径R=0.6893 nm下开角的临界值. 接下来研究不同管径下的能量变化，以此来得到不同管径下开角的临界值. 通过计算，从图5可以看到，对于不同管径，其开角的临界值基本上保持不变，(θ=16.3°左右)，各个管径下的临界值大小只有千分之一的误差，因此我们确定在不同管径下，CNT-GNR过渡体系，具有同样大小的临界开角.

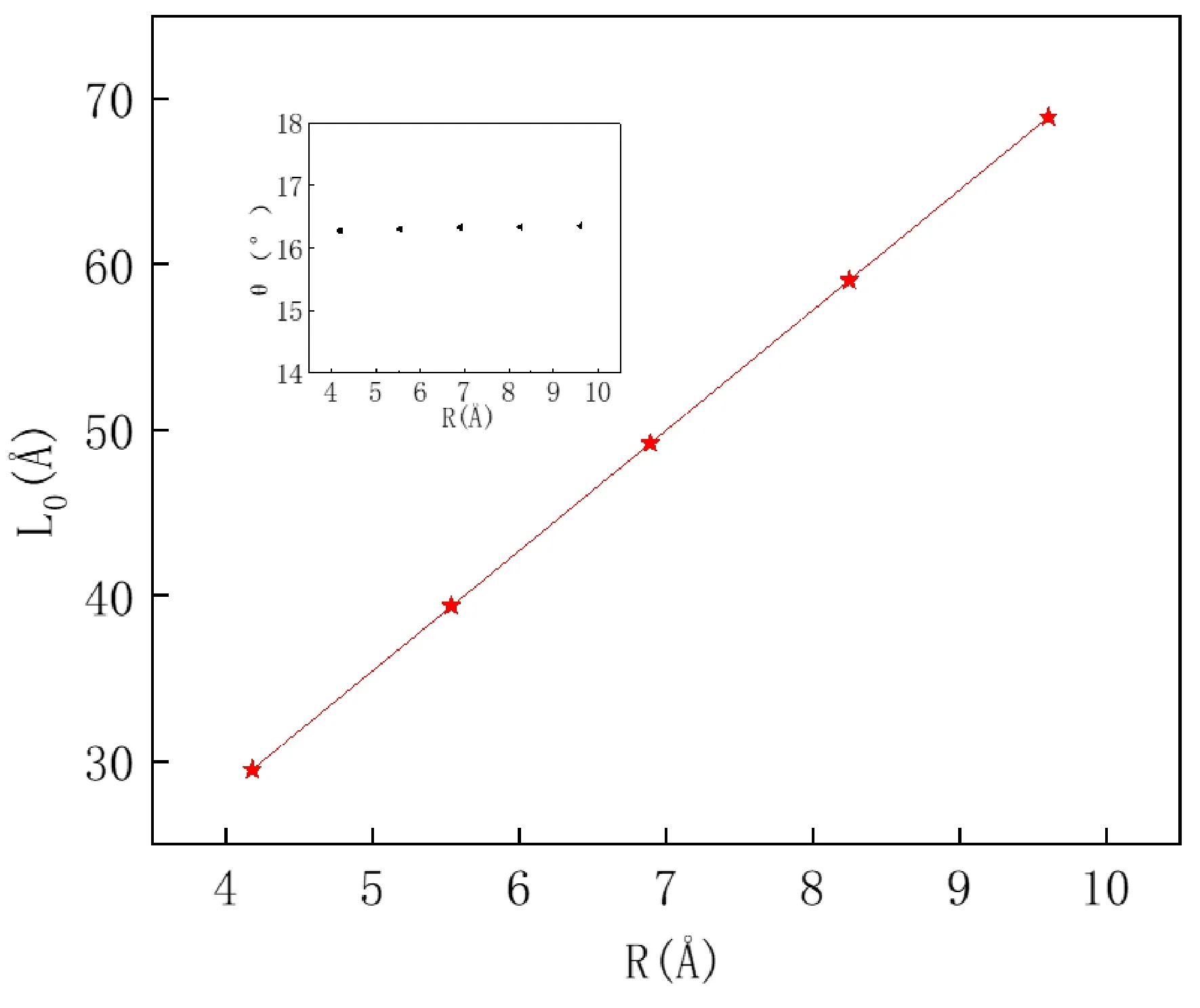
图5 不同管径下所对应的临界角与临界长度Fig.5 The critical angle and critical length corresponding to different pipe diameters

不仅如此，由于临界角的数值大小是通过L0与R的正切关系计算所得，因此在临界角大小不变的情况下，L0与R在数值上必定存在一定的函数关系，通过多组数据拟合得到图5所示的线性关系. 所以我们在确定一个管径的大小后便可知其过渡系统的最小长度，即临界长度L0：

L0=7.256*R-0.82

(3)

其中R为碳纳米管的管径.

3.3过渡系统热输运性质

利用NEMD模拟，计算了当开角小于临界值时的CNT-GNR的过渡连接处的局部热导率. 通过得到温度梯度，计算系统的总热阻，再通过傅里叶公式计算出左右两端(纯CNT和纯GNR)的热导率进而求出其热阻，最后得到过渡系统的热阻和热导率.

其中RI为连接碳纳米管和石墨烯纳米带过渡系统的热阻，lCNT是碳纳米管对应的长度，

(4)

kCNT为碳纳米管的热导率；lGNR是石墨烯纳米带对应的长度，kGNR为石墨烯纳米带的热导率; A是整个纳米带的横截面积. 为避免NEMD模拟中边界温度跃变的影响，我们使用温度梯度线性部分来计算Rtot以及碳纳米管和石墨烯纳米带的热导率. 表1总结了计算的整个体系的总热阻Rtot, 过渡系统的热阻RI以及过渡系统单位长度的热阻RI. 从表1可以看出随着开角θ逐渐增大至临界角前，整个体系热阻变化不大的情况下，过渡系统的热阻随之减小；并且过渡系统单位长度的热阻也随着开角的增大而减小，这是由于对不同大小开角的单位长度来讲，开角越大，则意味着在这个过渡系统中，石墨烯所占比重增大，此时石墨烯的热输运性质占主导地位，反之碳纳米管的热输运性质占主导地位，且相同条件下石墨烯的热导率[7-11]大于碳纳米管的热导率[28-29]，在本研究的体系中，碳纳米管的热导率为178 W/mK,石墨烯纳米带的热导率为253 W/mK,因此出现上述结果.

在得到了过渡系统的热阻后，我们进一步计算得到其热导率的大小. 当过渡系统开角较小，即卷起部分过多时，此部分结构非谐性情况增加，导致声子散射缩短了声子的平均自由程，从而导致较低的热导率. 热导率随开角变化的关系与热阻变化一一对应. 对于同一管径，在小于临界角的时候，热导率随着开角的增大而增大. 为了确定这样的变化关系并不是偶然的，又计算了不同管径下热导率的变化关系. 如图六所示，同样的结果也出现在另一管径中. 因此这样的变化关系是对于任何管径的纵向拉开的碳纳米管都适用的.

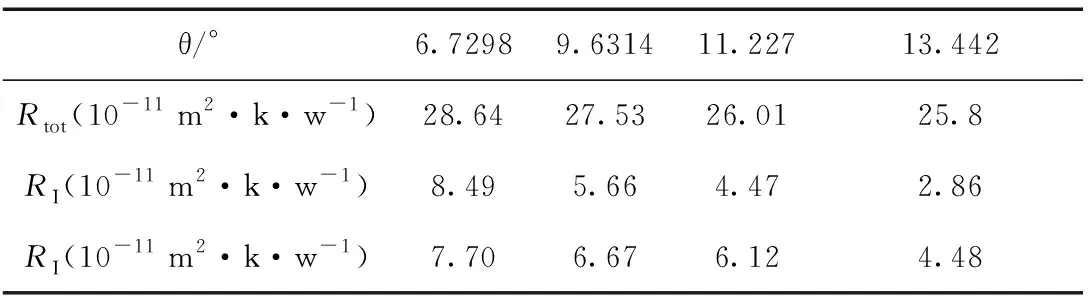
表1 计算得到的热阻值

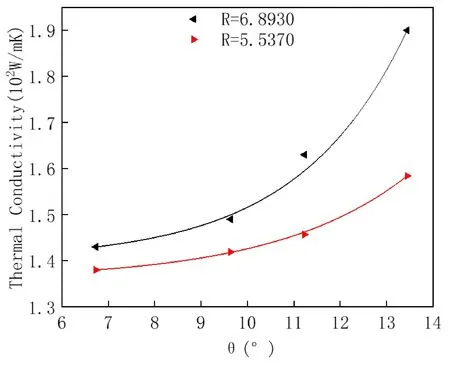
图6 两个管径下不同开角的热导率大小Fig. 6 The thermal conductivity of two pipe diameters at different opening angles

3.4声子态密度(PDOS)

为了进一步了解原子的振动特性，分别计算了碳纳米管，石墨烯和过渡结构的声子态密度. 在这三个区域中，20 ps内每隔1 fs记录一次原子速度，然后将原子速度的自相关函数建立傅里叶空间变换，计算出PDOS数值：

图7 三个区域内的归一化声子态密度Fig. 7 The normalized phonon state density in three regions

(5)

(6)

总态密度如图7所示. 对于这三个区域而言，其态密度都在17 THz和51 THz附近出现峰值，但过渡区域的态密度峰值相对于碳纳米管和石墨烯带有着明显的降低，这是由于过渡区域的存在缺陷，碳碳原子间非谐性振动增加，导致声子贡献减小.

4结 论

通过非平衡态分子动力学模拟，我们计算了CNT-GNR过渡系统的力学稳定性和热传导性质. 研究发现，即使碳纳米管的管径大小不同，但其能打开的最大角度都是一样的，临界值大小都为θ=16.3°. 在临界值以内，过渡系统的热导率可随着开角的增大而逐渐增大，这对于任意管径的碳纳米管纵向拉开为石墨烯纳米带的体系都是适用的. 本文对于研究一维和二维体系连接过渡的结构和性质具有重要的意义，还能为相关结构的制备提供有用的信息.