外电场下C4F7N分子的结构与特性

李亚莎, 周 筱, 孙林翔， 章小彬， 孟凡强， 梅益明

(三峡大学 电气与新能源学院， 宜昌 443002)

1引 言

六氟化硫(SF6)常温常压下无色、无臭、无毒、无腐蚀性、不易燃，具有极强的化学惰性，被广泛运用于很多行业，同时因其具有优良的绝缘性能和灭弧性能而被大量运用于电力行业．但研究表明，SF6气体具有较强的温室效应[1,2]，其温室效应作用是CO2的2.39万倍，《京都议定书》于1997年将其列为六种主要的温室效应气体之一，2016年的《巴黎协定》中也明确要求在本世纪下半叶实现温室气体净零排放，因此很多行业都大量减少甚至完全替换了SF6的使用[3]. 近年来，电力行业很多学者也逐步转向SF6替代气体的研究，替代气体需满足优质环保性能、强大电气性能两大核心要求．

其中，C4F7N(全氟异丁晴)自提出以来一直备受关注．C4F7N气体无色、无味且在700℃下化学性质稳定，全球变暖潜能值(GWP)约为2200，其臭氧消耗潜能值(Ozone Depression Potential, ODP)为0，绝缘性能是SF6的2.2倍以上，具有高电负性[4-6].但其液化温度较高(一个大气压下约为-4.7℃)，主要通过与低液化温度的CO2、N2等气体混合来解决此问题．纯C4F7N的毒性也比纯SF6要高，但其混合气体的半致死浓度与纯SF6相当[7]. 由于应用较少，所以价格要高于SF6．目前针对C4F7N的相关研究既采用实验手段也通过分子模拟方法，宏观与微观研究并行，全方位挖掘、分析C4F7N作为SF6替代气体的潜能．实验方面，西安交通大学的李兴文[8]等结合饱和蒸气压特性与临界击穿场强数据，研究了新型环保气体C4F7N与CO2混合气体的绝缘性能．武汉大学的周文俊[7]等研究C4F7N/CO2混合气体在均匀电场与极不均匀电场下的击穿特性．华北电力大学屠幼萍[7]等研究了直流电压下C4F7N/CO2混合气体的击穿电压、闪络电压和局放起始电压特性．分子模拟方面，武汉大学张晓星[9]等基于密度泛函理论和过渡态理论研究了C3F7CN在微水环境下的放电分解机理．李兴文[10]等基于从头算法使用改进的Deutsch-Märk(DM)公式计算了C4F7N的总电子碰撞电离截面．三峡大学李亚莎[11]等基于密度泛函理论研究了外电场下C3F7CN分子的电负性与福井函数特性．目前对于电场环境下C4F7N分子自身微观结构特性的研究鲜少.

分子模拟能够从微观角度深入探究气体分子自身的特性，通过量化计算为实验现象提供数据支撑．密度泛函理论(density functional theory，DFT)[12-15]是一种量子化学分析方法，它利用空间电子密度的泛函对多电子系统的性质进行考察，在处理电子体系的问题上简单精准．本文采用密度泛函理论中的M06-2X泛函在6-311g(d, p)和aug-cc-pVTZ基组水平，计算了C4F7N分子在外电场下的几何结构、Mulliken电荷布局、总能量、红外光谱、原子偶极矩校正的Hirshfeld布居(ADCH)、偶极矩和极化率，分析了外电场对它们的影响，揭示了分子微观结构与外电场的关系，为今后的相关研究提供了理论支撑与数据参考.

2理论和模拟方法

2.1理论方法

外电场作用下分子体系的哈密顿量H如下式所示[16, 17]：

H=H0+Hint

(1)

其中H0为无电场下体系的哈密顿量，Hint为外电场对体系作用的哈密顿量.在偶极近似的情况下，分子体系与外电场相互作用哈密顿量表示为[18]：

Hint=-μ·F

(2)

其中，μ是体系分子在外场下的偶极矩，F为外电场作用力．

分子系统的能量可以写成关于均匀外部电场F的Taylor展开，如下：

(3)

(4)

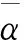
(5)

其中，αxx、αyy、αzz为极化率张量的对角元．

原子电荷，是对化学体系中电荷分布最简单、最直观的描述方式之一．计算原子电荷的方法诸多[20]，比如Mulliken方法、Hirshfeld方法、ADCH方法等，各自具有不同的优缺点．其中Mulliken电荷算法简单，计算量小，但基组依赖性大，弥散函数对其有很大破坏性，偶极矩重现性不理想．Hirshfeld电荷数值普遍偏小，而且偶极矩、静电势重现性比较差，其主要原因是原子偶极矩被完全忽略．ADCH是对Hirshfeld方法的校正,将每个原子的原子偶极矩扩展为相邻原子处的校正电荷，所有原子偶极矩展开成校正电荷后,将校正电荷累加到原始Hirshfeld电荷上就得到了ADCH电荷，校正后原子电荷普遍增大，且更加符合化学实验值与理论值．ADCH原子电荷的化学意义十分合理，分子偶极矩被精确再现，静电势的重现性也较好，电荷计算时间也远小于波函数计算时间．

ADCH[21]方法首先计算各个原子的Hirshfeld电荷及原子偶极矩，假设我们想要扩展原子A的原子偶极矩作为校正电荷，显然，所有校正电荷之和应为零，根据校正电荷计算的偶极矩应与原子偶极矩完全相等，即满足以下条件

(6)

(7)

其中，ΔqA→B是从原子A转移到B的电荷，也就是A对B的校正电荷，RB是B原子相对于A原子的相对坐标(列向量)．要想校正电荷仅在邻近A的原子周围分布，那么采用最小化函数F来实现：

(8)

其中，α和β是用来满足这两个约束条件的拉格朗日乘数，υAB是随着A和B之间距离的增加而迅速减小的函数，F的设计抑制了远离原子A的原子上出现大的校正电荷．

与此同时，ADCH是偶极矩保守的方法,因此由ADCH电荷导出的偶极矩与实际偶极矩保持高度的一致．

2.2模拟方法

搭建C4F7N分子模型如图1所示，分子关于C-N键方向左右对称．基于密度泛函理论，沿5N-4C轴向施加步长0.005 a.u.，范围0-0.040 a.u.的电场，采用明尼苏达密度泛函M06-2X在6-311g (d, p) 基组水平上对分子进行基态几何优化和频率计算，读取不同电场强度下的分子结构、Mulliken电荷布居、总能量以及红外光谱 (Infrared spectra，IR) ．

另外，计算合理的偶极矩与极化率，弥散函数起着至关重要的作用，所以提升基组水平且增加弥散函数成为不可或缺的考量，aug-cc-pVTZ基组级别对此具有优质的适用性．于是在该外场范围内，采用明尼苏达密度泛函M06-2X在aug-cc-pVTZ基组水平上对C4F7N分子进行几何优化和频率计算，计算不同电场强度下的分子极化率，结合Multiwfn[22, 23]软件计算ADCH原子电荷与偶极矩．

图1 C4F7N分子模型Fig. 1 Molecular model of C4F7N

3结果与分析

3.1外电场对分子结构和能量的影响

使用明尼苏达密度泛函M06-2X/6-311g (d, p)对C4F7N分子做优化和频率计算，在0-0.04 a.u.电场范围内的基态键长数据与Mulliken电荷布局分别如表1和表2所示．

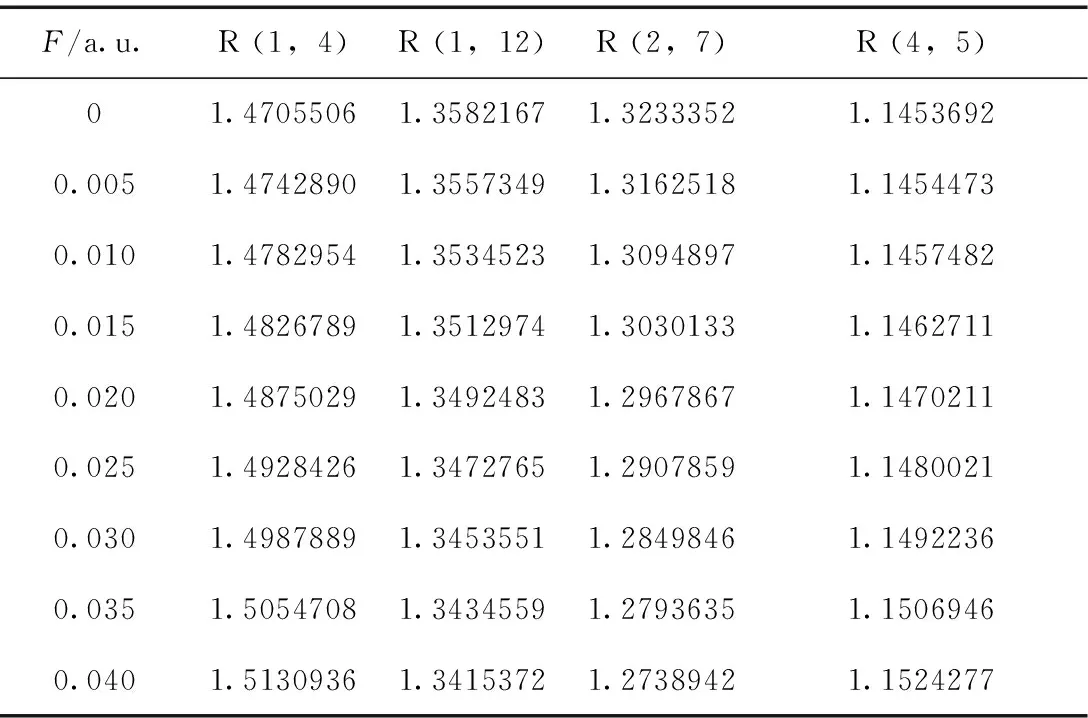
表1 不同电场强度下C4F7N分子的键长/Å

由表1可知，分子键长和电荷布居对外电场有很强的依赖关系．对于C4F7N基态分子，随着电场的增加，R(1,4)、R(4,5)键长增大，R(1,12)、R(2,7)键长减小，变化规律如图2所示，分子几何参数的变化可以用电荷转移引起分子内电场的变化以及内外电场的叠加效应来定性解释[24, 25]. 由表2，5N原子由于其电负性所以电荷布居为负，那么内电场方向由4C指向5N．随着外电场的增大，4C的电荷布居数逐渐增大，而5N的电荷布局数逐渐减小，电子转移到5N上，4C-5N间的内电场减小，R(4,5)增大.

表2 不同电场强度下C4F7N分子的Mulliken电荷布居

图2 R(1,4)、R(4,5)、R(1,12)、R(2,7)键长随电场强度的变化Fig. 2 Variations of bond lengths of R(1,4)、R(4,5)、R(1,12)、R(2,7) with electric field intensity

图3 C4F7N分子总能量随电场强度的变化Fig. 3 Variation of total energy of C4F7N molecule with electric field intensity

图3所示为C4F7N基态分子的总能量E随电场的变化情况，可以看出，随着电场的增强，E逐渐减小，且减幅逐渐增大．这主要是由于随着正向电场的增大,电子朝5N方向偏移，其电荷布居数绝对值增大，从而使得体系的哈密顿量H的势能增大(数值上)，进而使得体系的总能量降低[24]，所以分子的总能量呈减小态.

3.2外电场对分子红外光谱的影响

使用明尼苏达密度泛函M06-2X/6-311g(d, p)对分子做频率计算，得到C4F7N分子在外电场分别为0，0.020，0.040 a.u.时的红外光谱，如图4所示．图中给出了无外电场时的6个特征峰，波数1376.41 cm-1处的吸收峰对应于2C-1C-3C的剪式振动，当电场强度增大时，出现了明显的蓝移现象，这是因为电场的增大改变了原子的电荷布居，使其键能增大．而波数1329.27 cm-1处的吸收峰对应于2C-1C-3C的面外摇摆，波数1231.97 cm-1处的吸收峰对应于以1C为核心的四个C原子的对称变形振动，波数1114.31 cm-1处的吸收峰对应于1C为核心的1C-2C-3C-12F之间的对称变形振动，波数1027.49 cm-1处的吸收峰对应于12F-1C-4C的面外摇摆，波数746.23 cm-1处的吸收峰对应于2C-1C-3C的面内摇摆，此时的吸收强度很弱，随着电场的增强这5个吸收峰均发生明显的红移现象，亦是电场改变了原子的电荷布居，使得相应键能减小的缘故.

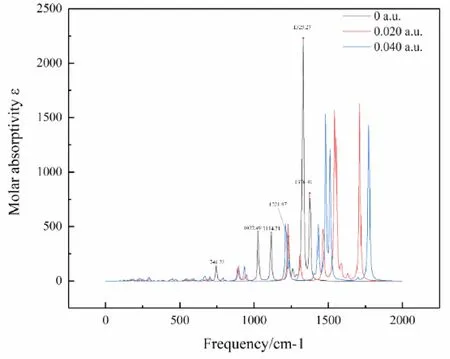
图4 C4F7N分子在不同电场强度下的 IR 光谱Fig.4 Infrared spectra of C4F7N molecules under different electric field intensities

3.3外电场对分子偶极矩和极化率的影响

采用明尼苏达密度泛函M06-2X/aug-cc-pVTZ对C4F7N分子做优化和频率计算，结合波函数分析软件Multiwfn计算ADCH原子电荷、偶极矩和极化率，分别如表3所示．使用Multiwfn+VMD以原子着色的方式将电场强度为0和0.04 a.u.的ADCH电荷表现如图5所示.

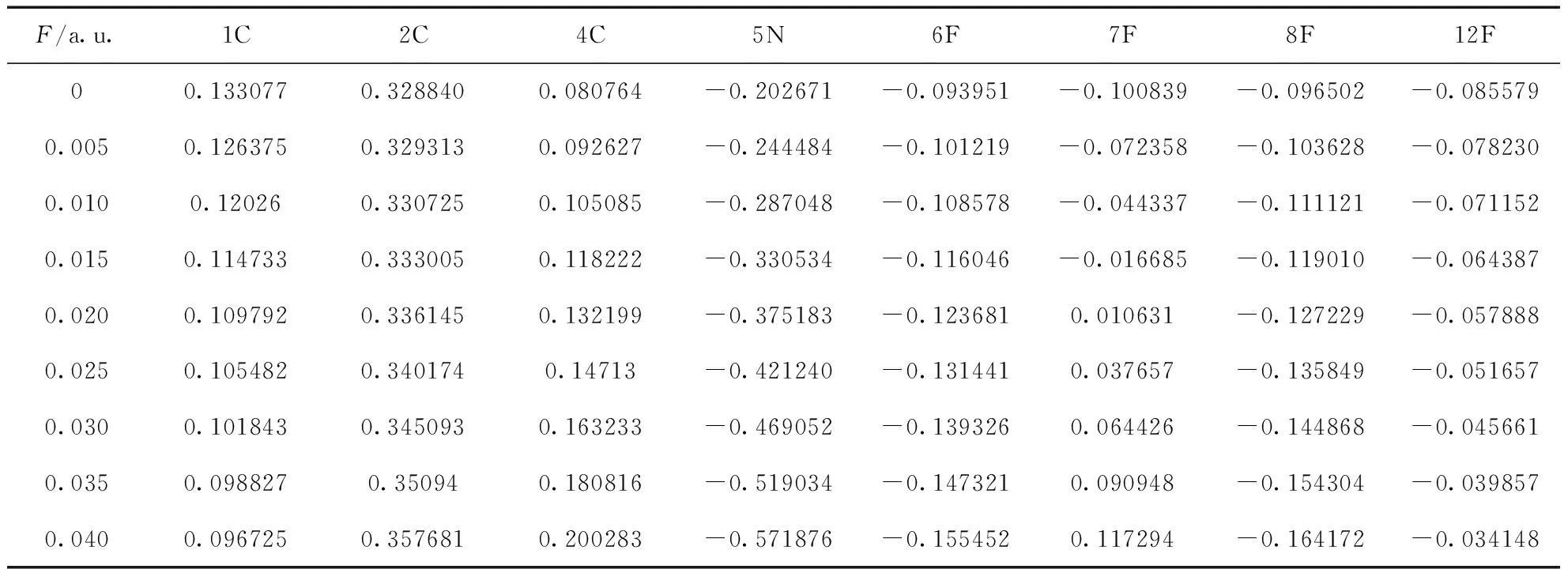
表3 不同电场强度下C4F7N分子的ADCH原子电荷

表4 不同电场强度下C4F7N分子的偶极矩和极化率

图5 不同电场强度下的ADCH原子电荷着色图(a)电场强度为0；(b)电场强度为0.040a.u.Fig.5 Coloring maps of ADCH atomic charges under different electric field intensities(a)the electric field intensity is 0; (b) the electric field intensity is 0.040a.u

图5根据原子的电荷值来着色，蓝色表示原子带负电荷，红色表示原子带正电荷，颜色越深表示带电荷数越多．C4F7CN分子属于左右对称结构，结合表3和图5分析，所有C原子均带正电荷，其中4C所带正电荷随着外电场的增强而显著增加；5N带负电荷，且所带负电荷数值在所有带负电荷原子中均保持最大，电场增强，其所带负电荷增多；当电场为0时，F原子均带负电荷，随着外电场增强直至0.040 a.u.，7F与10F从带负电荷变为带正电荷，12F所带电荷逐渐趋于0，而余下的F原子所带负电荷均有明显增加.

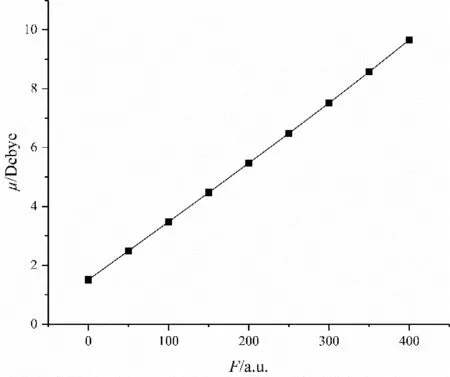
图6 C4F7N分子偶极矩随电场强度的变化Fig.6 Variation of dipole moment of C4F7N molecule with electric field intensity

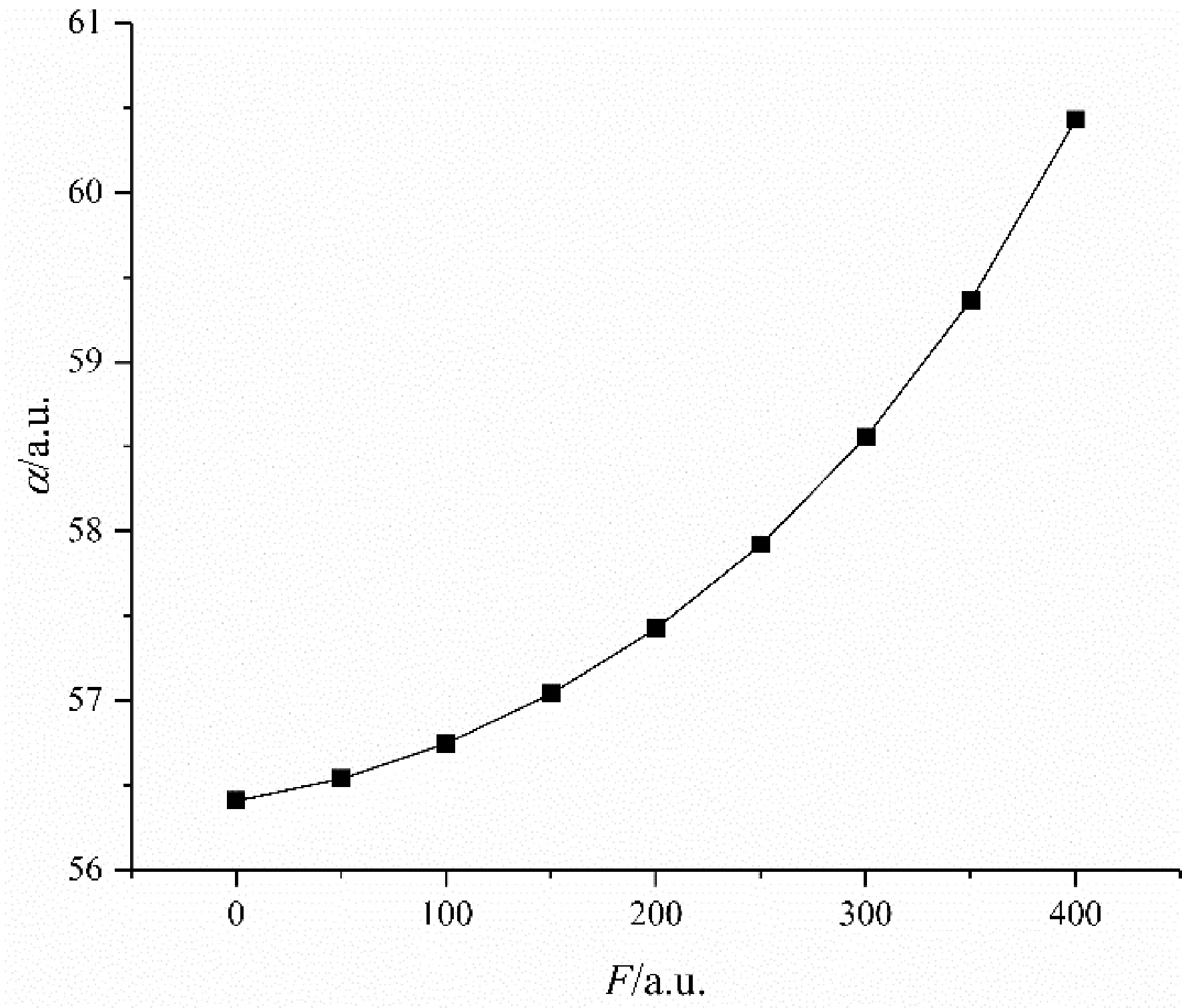
图7 C4F7N分子极化率随电场强度的变化Fig. 7 Variation of polarizability of C4F7N molecule with electric field intensity

图6和图7分别是外电场下C4F7N分子偶极矩和极化率的变化情况，显然，偶极矩随着外电场的增强而增大，且几乎呈线性增长．极化率随着外电场的增大而逐渐递增，且增幅越来越大.分子极性发生改变，稳定性减弱，同时分子偶极矩逐渐增大，由于分子空间体积有限，原子核对电子的吸引力也有限，若外电场增大到一定值，分子偶极矩会达到极限值，最终导致化学键发生断裂，产生游离自由基，致使发生击穿[16].

4 结 论

本文采用DFT/M06-2X方法在6-311g(d,p)基组水平计算分析了外电场下C4F7N分子的基态几何结构、分子能量与IR光谱，在aug-cc-pVTZ基组水平计算研究了外电场对C4F7N分子ADCH原子电荷、偶极矩以及极化率的影响．在DFT中，一般的几何优化、振动分析对基组的敏感度不大，所以不必要使用大基组，且不需要太多高角动量基函数，使用6-311g(d, p)这样的中等基组完全足够，而偶极矩、极化率分别是能量对外电场的一阶、二阶导数，其计算务必要考虑弥散函数，而且随着导数阶数的增加，对弥散函数要求越来越高，同时ADCH原子电荷不受弥散函数影响，aug-cc-pVTZ基组级别较为理想.研究表明：上述参数对电场具有明显的依赖性．

(1)C4F7N分子关于C-N键方向呈左右对称状，所加电场沿5N-4C键方向，所以左右两个CF3基团的键长、Mulliken电荷布局以及ADCH原子电荷在不同电场强度下的变化表现出很好的同步性．

(2)分子中R(1,4)、R(4,5)、R(1,12)、R(2,7)键长变化明显，外电场作用下电子发生转移，分子内外电场的叠加效果发生变化，导致R(1,4)、R(4,5)键长增大，R(1,12)、R(2,7)键长减小．同时C4F7N基态分子的总能量随着电场的增强而逐渐减小，减小幅度越来越大．

(3)不同电场强度下，C4F7N的吸收峰主要集中于高频区，既有红移也有蓝移，振动形式多样.

(4)外电场下，ADCH原子电荷变化明显，主要变化集中在F原子、4C和5N上．同时偶极矩和极化率均随着电场增强而增大，分子稳定性减弱．