基于局部近邻标准化和主多项式算法的故障检测

李 元,杨东昇,冯立伟,张 成

(1.沈阳化工大学 信息工程学院,辽宁 沈阳 110142；2.沈阳化工大学 数理系,辽宁 沈阳,110142)

随着现代化工业生产过程系统正快速向着大型化、高度自动化和高度复杂化发展，故障检测技术逐渐在保证生产过程安全、提高产品质量、保障工厂安全等方面做出巨大贡献，也显示出该研究方向巨大的学术研究价值[1-5]。

主元分析(PCA)算法是一种多元统计算法，现已被广泛应用于工业过程故障检测。基于PCA算法的过程监控具有简单、可逆性强、可直观解释等优点，其本质为建立一种正交变换，通过线性方法将原始数据空间分解为主元子空间和残差子空间，同时应用T2和SPE对工业过程进行监控[6]。然而，基于PCA的方法假设监控过程是线性的，且计算统计量T2和SPE时需要假设过程数据服从单模态的多元高斯分布，这就限制了它在非线性多模态工业过程中的应用[7]。针对非线性问题，基于核技巧的核主元分析方法如Kernel、PCA和KPCA等方法被提出[8-9]。KPCA通过将原始数据映射到高维希尔伯特空间，在此空间中使用PCA算法进行故障检测，与传统的PCA方法相比，通过将低维数据映射至高维空间，增大样本数据在高维空间中线性可分的可能性，但是因核方法不具备可逆性和直观解释性，且监控时使用的仍是T2和SPE统计量，因此其在多模态故障检测中同样具有一定的局限性。Hsieh和Kramer等[10-11]提出的非线性PCA(Nonlinear PCA,NLPCA)，也是PCA非线性扩展方法，通过神经网络将数据映射到特征空间，但是由于公式中的非线性特征并不明显，因此在进行故障诊断时，很难通过计算过程变量对故障进行定位。Zhang等[3，12]提出了基于PPA的故障检测方法，利用一组灵活的主多项式分量来描述数据的非线性结构，但由于与PCA一样使用T2和SPE统计量，因此在多模态过程中检测效果受到限制。针对多模态问题，目前常用的建模方法主要分为两大类：①局部建模，通过聚类方法将多模态数据分离，再对每个模态进行局部建模，此类方法求解步骤成熟，但是获取工业数据所属的模态仍是一大难点；②全局建模，通过对多模态数据进行处理，再使用单一的模型训练多模态数据。Ma等[13]提出了一种局部近邻标准化方法，通过建立样本的近邻数据集，再使用近邻集的均值和标准差对当前样本进行标准化，消除数据中的多模态结构，并使得数据近似服从单模态高斯分布。

本研究针对非线性多模态工业过程，提出了一种基于局部近邻标准化和主多项式分析的故障检测方法。首先由LNS算法处理原始多模态数据，再通过PPA方法建模寻找数据中的非线性特征，计算其监控统计量来进行故障检测。LNS-PPA方法继承了LNS和PPA处理多模态和非线性的优势，可以有效地对具有多模态和非线性特征的工业过程进行故障检测。

1 主多项式分析算法

PPA通过使用一组主多项式成分从过程数据中学习数据的低维表示，将PCA中的直线主成分更换为曲线的主多项式成分，以更好地捕捉过程变量间的非线性特征[14]。

在PPA建模阶段，假设采集到正常工况下的训练数据X∈Rd×N为d个测量变量，N个训练样本，PPA对原始数据X的分解如下所示[15]：

(1)

(2)

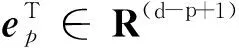
(3)

Vp=[vp,1,vp,2,...,vp,N]。

(4)

在线故障检测中，得到一个观测数据xnew∈Rd，根据(1)和(2)，可以得到第p步的主多项式得分anew为：

(5)

(6)

(7)

其中ΛPPA∈Rρ×ρ为对角矩阵，其对角元素为主多项式分量的方差。PPA的SPE统计量定义如下：

(8)

(9)

2 基于LNS-PPA的故障检测策略

基于PPA的方法虽然能够在非线性工业过程下发挥出色的性能，但是它同样使用T2和SPE统计量进行过程监控，因此在多模态工业状态下，将影响PPA的检测性能。

常用的Z-score标准化方法在针对单模态样本处理时，将数据进行平移和缩放使得数据的中心平移到新坐标系的原点[17]。但是因为Z-score方法使用的是全局均值和标准差，并没有考虑多模态数据分布的不同，因此经过Z-score方法处理后的数据并没有消除其多模态特征，最优的解决方法是通过计算每个模态的均值和标准差对当前模态进行标准化，但是在实际生产过程中，其数据所属的模态很难确定，因此基于局部近邻标准化的方法被提出。

局部近邻标准化方法主要思想是对每个样本寻找其k近邻样本，构建其对应的近邻数据集，再通过近邻数据集的均值和标准差对其原始样本进行标准化，使用局部近邻数据的均值和标准差来近似的代替全局数据的均值和标准差。假设原始数据为X，LNS确定X中的每个样本xi的k近邻数据集n(xi),再求出xi的k近邻数据集的均值m(n(xi))和标准差std(n(xi))，最后使用近邻集中的均值和标准差对当前样本xi进行标准化，如下式：

(10)

由上可知，LNS方法能够有效的降低多模态数据中心漂移和方差差异明显对后续故障检测方法带来的不利影响，且能够将多模态数据融合为近似服从高斯分布的单一模态数据。为了扩展PPA方法在多模态工业数据下的检测性能，本研究提出了一种基于LNS-PPA的故障检测方法，其步骤可分为离线建模和在线检测两步。

a)离线建模

1) 获得正常的过程数据X。

2) 使用局部近邻算法找到每一个样本xi对应的近邻数据集n(xi)。

3) 使用式(10)对每一个样本进行标准化处理。

4) 在标准化处理后的数据上构造PPA模型，得到对应的主多项式分量与残差分量。

5) 分别在主多项式分量空间和残差空间计算统计量T2和SPE。

7) 保存训练模型中所用的参数ep,vp,Ep和Wp。

b) 在线检测

假设测试样本Xnew

1) 在训练数据X中寻找到Xnew的k近邻集，同样应用式(10)进行标准化处理。

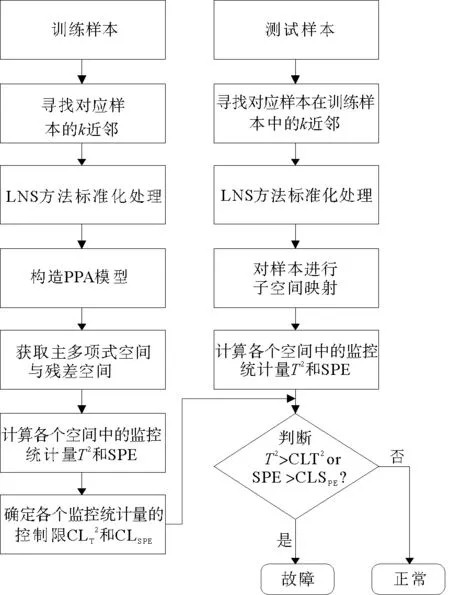
图1 LNS-PPA故障检测步骤

2) 利用训练模型中所保存的参数将测试样本Xnew映射到主多项式空间和残差空间，并在对应空间求得T2和SPE统计量。

3) 将上步求得的统计量与离线建模步骤中的控制限进行对比，若T2和SPE任一统计量超过其对应的控制限，则认为该样本为故障样本。

3 数值例子

使用Ge和Song文献[18]中提出的非线性系统多模态数值例子，其主要模型由式(11)组成：

(11)

其中e1～e5为服从[0，0.01]正态分布的噪声；s1和s2为系统的主要控制变量，通过改变s1和s2用来对系统的模式进行调整，以此产生多模态数值例子；两种模态数据的产生分别如式(12)和式(13)所示：

(12)

(13)

使用上式中的参数在每个模态下生成400个正常数据构成训练样本。

为了证明所提出的方法能够解决多模态非线性问题，通过在不同模态的样本中添加扰动以引入两种不同故障，具体操作如下[19]：

1) 在模态1的情况下，对变量x2从第201个样本至400个样本上添加0.2(k-200)来引入斜坡故障；

2) 模态2的情况下，对变量x5从201个样本至400个样本上添加幅值25%的阶跃故障。

其故障变量如图2所示。

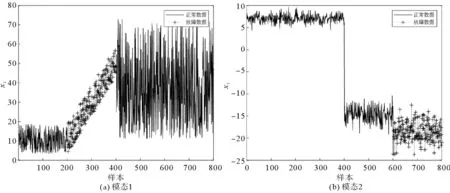
图2 引入的故障类型Fig. 2 Type of fault introduced

接下来使用PCA、PPA和LNS-PPA对此数值例子进行建模分析，通过85%累积贡献率确定PCA中的主元个数为2，PPA和LNS-PPA中的主多项式成分设置为2，LNS-PPA中的局部近邻个数k设为50。图3～4为故障变量x2和x5的散点分布图，从图3中可以看出原始数据中的多模态分布，且多模态数据不满足PCA和PPA方法中T2和SPE统计量对过程数据分布的假设，因此PCA和PPA的检测率较低。而LNS方法通过寻找样本的局部近邻数据集，使用局部的信息对样本进行标准化，将多模态数据缩放至各个模态的中心，如图4所示，可以看出LNS方法能够将原始多模态数据近似融合为服从高斯分布的单一模态，且因为PPA能够很好的处理非线性问题，因此LNS-PPA具有较高的检测率。以上三种方法对本文的数值例子检测效果如图5所示。

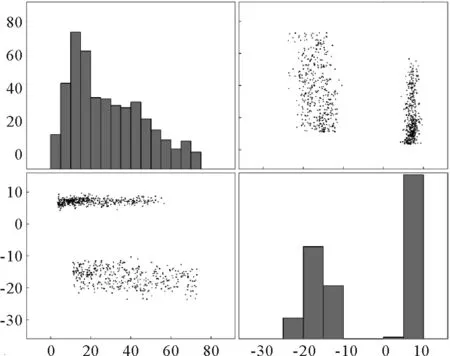
图3 原始样本故障变量散点图及对应的分布Fig. 3 Scatter plots of the original sample fault variables and their corresponding distributions

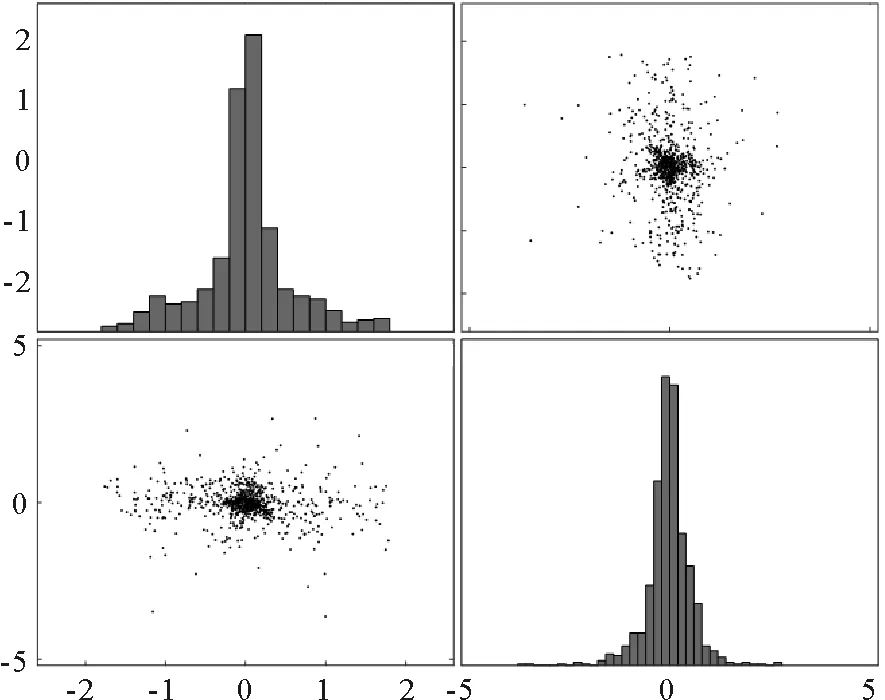
图4 LNS处理后的故障变量散点分布图及对应的分布Fig. 4 Scatter distribution map of fault variables after LNS processing and corresponding distribution

图5 PCA、PPA和LNS-PPA方法对数值例子的检测结果Fig. 5 Detection results of numerical example for PCA、PPA and LNS-PPA

表1 TE过程生产模式Tab. 1 TE process production model

4 LNS-PPA在TE工业过程的应用

田纳西-伊斯曼过程由伊斯曼化学品公司创建，目的是为了评价过程控制和监控方法提供一个现实的工业过程[20]。该过程是对一个真实工业过程的仿真，作为比较各种方法的数据源，已经在故障检测方面得到了广泛的应用。本文仿真实验使用的为TE过程生产模式1和3，不同模式的生产过程根据生产物G/H的比例来划分，具体如表1所示，将两个模态的数据混合使用，即训练数据为960个，用于检测的样本数为1 920个，其中包含各个模态的160个正常数据和对应故障的800个样本[21]。

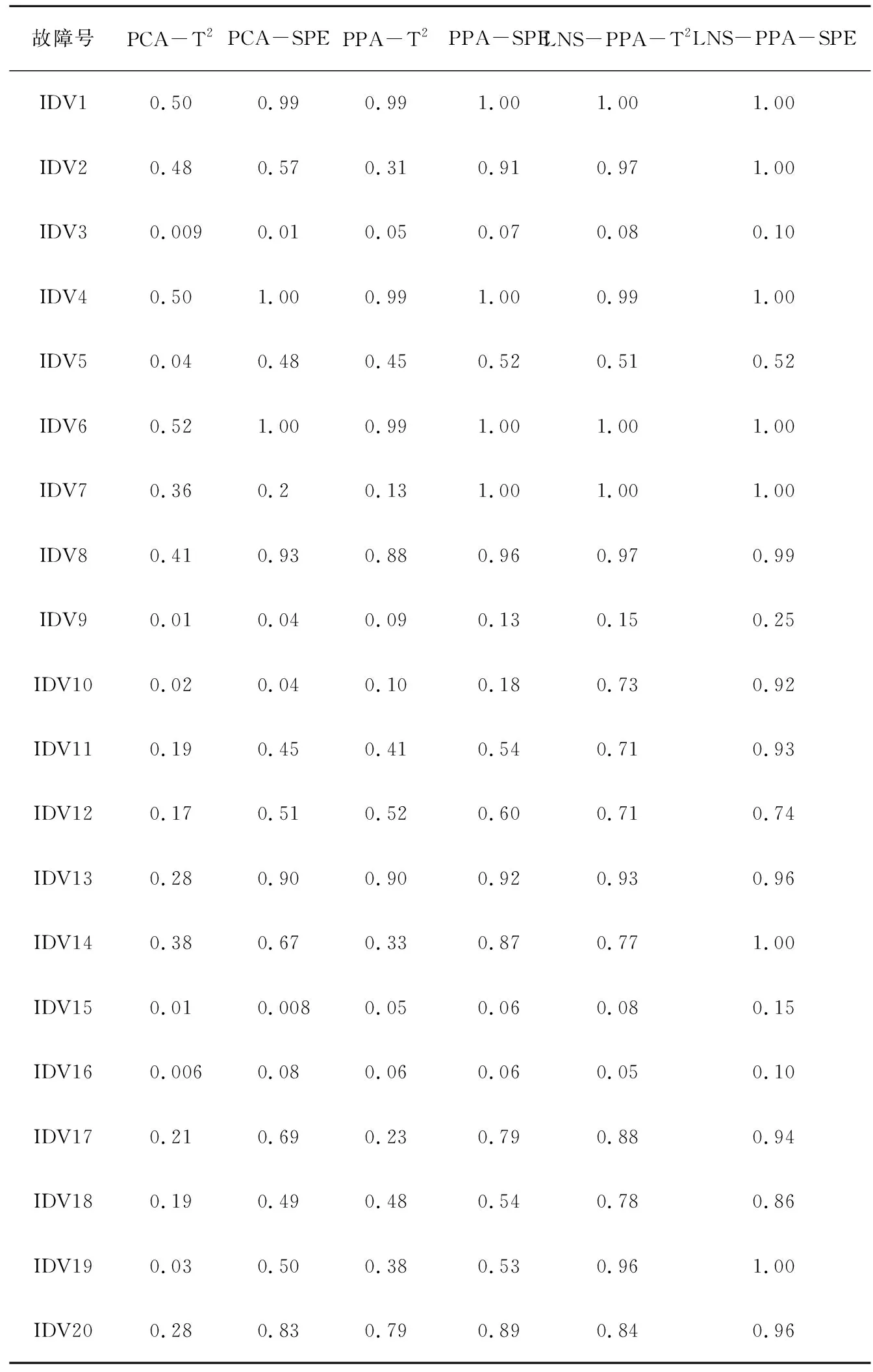
表2 三种方法的检测率汇总表Tab. 2 Summary of detection rates for three methods

下面对提出的LNS-PPA检测方法在TE过程中的20个故障检测中的有效性进行研究，其中PCA的主元个数通过85%的累积贡献率求得为28；PPA的主多项式空间设为4，主多项式的幂设为4[14]； LNS-PPA的主多项式空间与多项式阶数与PPA方法的参数一致，通过试错调参得到近邻集的个数k为150；监控统计量的控制限均设置为99%，表2中包含了基于PCA、PPA、LNS-PPA方法分别在TE过程的20种故障中所得出的检测结果。从表2中可以看出，本LNS-PPA方法能够提供监控多模态TE过程中大多数故障的最佳结果。

由图6看出，原始数据变量间的多模态结构十分明显，经过LNS方法处理将多模态数据近似的转换为服从高斯分布的单模态数据，其结果如图7所示。

由表2可知，LNS-PPA方法与PCA、PPA对故障1，4，5，8，13，20均具有良好的检测性能，其故障检测率均高于80%，而对于故障2和19，PCA与PPA的检测效果均低于LNS-PPA方法。其中故障2 是一种阶跃故障，由于进料含量的变化使得一系列相关变量偏离正常范围，PCA和PPA方法均未有效的检测到故障的发生。如图8所示，其中采样数为0至960和961至1 920的样本分别为工作模式1和3条件下采集的观测样本，明显看出受多模态特征的影响，PCA和PPA的监测统计量大多数均在控制限以下。其主要原因是PCA和PPA方法的全局建模方式并不适用于描述多模态工业数据，单一检测模型受多模态中心不一致和方差差异明显特征的影响，使得模型描述的正常区域范围较大，对工业过程中的随机故障并不敏感，因此PCA和PPA的检测效果较差。故障19是一种未知故障，PCA和PPA的检测效果如图9所示。由于PCA和PPA方法使用正常数据构建的控制限受到方差较大的模态影响，导致模态1的故障均未能有效地检测出。而在LNS-PPA方法中，样本经过LNS的处理后已经近似服从高斯分布，同时LNS使用每个样本局部近邻集的均值和方差代替全局信息消除了过程数据中的多模态特征，为PPA的检测提供了良好的数据基础，因此该方法在以上故障中的检测率最高。

图6 多模态TE过程变量散点图及对应分布Fig. 6 Scatter plot and corresponding distribution of multimodal TE process variables

图7 经过LNS处理后的多模态TE数据变量散点图及对应分布Fig. 7 Scatter plot and corresponding distribution of multimodal TE process variables after LNS processing

图8 三种方法的故障2检测结果Fig. 8 Detection results of three methods for IDV2

图9 三种方法的故障19检测结果Fig. 9 Detection results of three methods for IDV19

5 结论

提出了一种基于LNS-PPA的故障检测算法，通过LNS方法去除数据中的多模态结构，再使用PPA方法寻找一条曲线的主多项式分量来拟合数据中的非线性结构，最后通过非线性数值例子和田纳西伊斯曼多模态过程证明了基于LNS-PPA方法的故障检测算法的有效性与优越性。