射流式喷头水量分布动态仿真及试验

朱兴业，史永杰*，胡 广，刘俊萍

（1.中国农业科学院 农田灌溉研究所/河南省节水农业重点实验室，河南 新乡 453002；2.江苏大学 流体机械工程技术研究中心，江苏 镇江 212013)

0 引 言

【研究意义】喷灌均匀度是衡量灌溉质量和喷头水力性能的重要指标,是喷灌系统规划设计中的重要参数[1-4]。实践证明，在整个喷洒面积上喷洒的均匀度对作物的增产有决定性的影响[5]。为提高喷灌系统灌溉的均匀性，国内外不少学者在喷灌水量分布均匀性的计算以及喷头结构的改进等方面进行了大量研究。【研究进展】朱忠锐等[6]提出了一种计算有风条件下喷灌系统组合均匀度的方法。韩文霆等[13]分析了采样间距、插值方法、计算网格间距对均匀系数的影响规律。吕名礼等[3]利用Visual Basic 6.0开发出不同环境条件下单喷头或多喷头组合喷灌水量分布的模拟软件。汤攀等[9]建立了将实测平地单喷头水量分布图转换成坡地上单喷头水量分布图的计算模型。以往学者对喷头喷灌水量分布的模拟和均匀性评价，大多数学者都是对试验中测量点的径向水深进行分析处理，得到该喷头的水力性能。喷灌水量分布的模拟软件在对测量点进行数据处理过程中也较少考虑到旋转式喷头由于旋转的不均匀性导致不同径向方向上水量分布的不一致性。关于喷头改进和开发方面，朱兴业等[12]深入探索了国内原创旋转式射流喷头结构参数与喷洒均匀性之间的关系。刘俊萍等[8]根据射流理论分析设计了不同结构的副喷嘴，并对全射流喷头的变量喷洒均匀性进行了综合评价。许正典等[11]对垂直摇臂式喷头的可调工作参数进行了优化研究，使喷头运行时处于最优水力性能状态。【切入点】以上关于喷头结构的优化主要是针对中高压情况下，在低压工况下，摇臂式喷头在实际运行中由于压力不足会出现喷头水力性能下降的现象。【拟解决的关键问题】射流式喷头是通过信号水实现射流元件内部主射流的附壁，低压情况下会出现难以取得信号水的问题。因此，研发出低压工况下，结构简单、工作稳定的射流式喷头具有重要意义。

本文对全射流喷头射流元件进行了优化，选择合理的取水方式，提出一种新型射流式喷头，并采用新的水量分布计算方法对该喷头进行单喷头和多喷头组合喷灌水量分布动态仿真，探究出该喷头在不同工作压力和安装高度下的水力性能。

1 材料与方法

1.1 试验方法

喷头喷洒试验系统主要由水泵、电磁流量计、压力表、流量控制阀、压力调节器、回流阀、输水管、喷头和雨量筒等组成。试验在直径为44 m的室内无风喷灌实验室内进行，试验样机如图1所示，喷头安装高度分别为1.1、1.3和1.5 m，在工作压力分别为100、150、200、250和300 kPa的情况进行全圆喷洒。喷头连接压力调节器，工作压力由0.4级的精密压力表读出，喷灌水量采用内径为0.2 m、高为0.6 m的雨量筒测量，雨量筒以喷头垂下地面位置为中心辐射径向布置1条线，雨量筒间距为0.5 m，在喷头稳定运转10 min后开始试验，测试时间为1 h，每组试验重复3次。图2为喷头试验系统示意图，图3为雨量筒布置图。测出喷头旋转速度，采用 KB874红外对管、对射式光电开关、红外传感器等仪器设计如（图4）所示的装置测量喷头在11条射线方向上的瞬时速度，发射器安装在喷头旋转部位，接收器1、2分别安装在发射器正下方，相距0.5 m，固定在输水管上，当喷头旋转至接收器位置时，接收器1、2将接收到高频模拟信号，采用A/D转换器将其转换成数字信号并通过示波器显示出该两束矩形波，2束波形的时差即近似为喷头的瞬时速度。

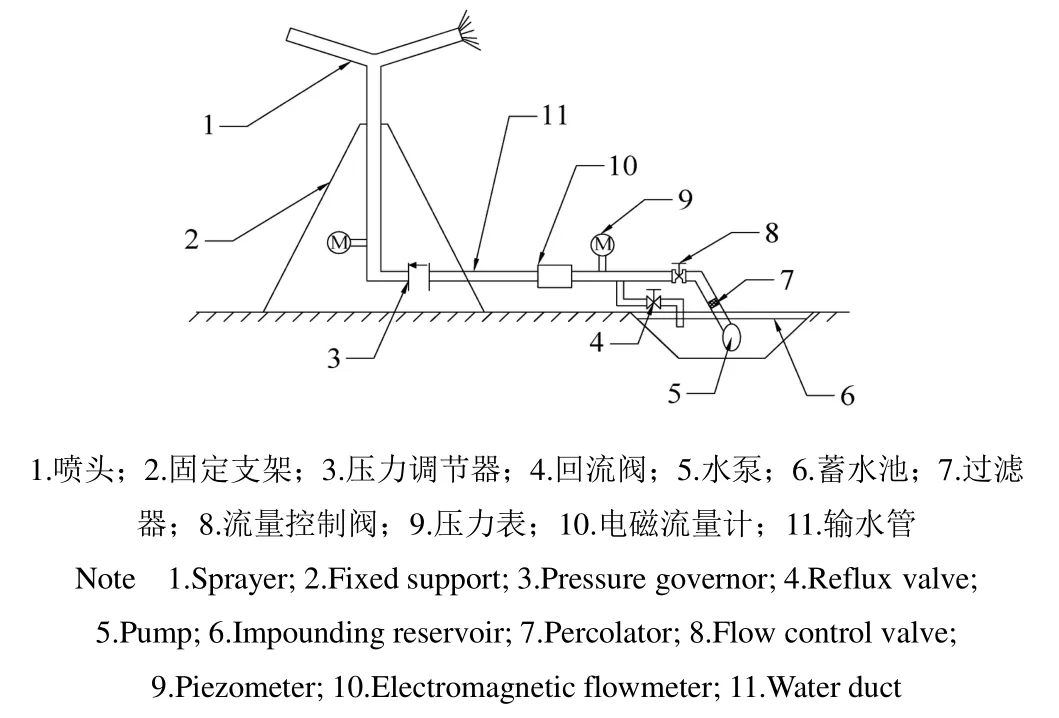
图2 喷头试验系统示意图Fig.2 Schematic diagram of sprinkler test system

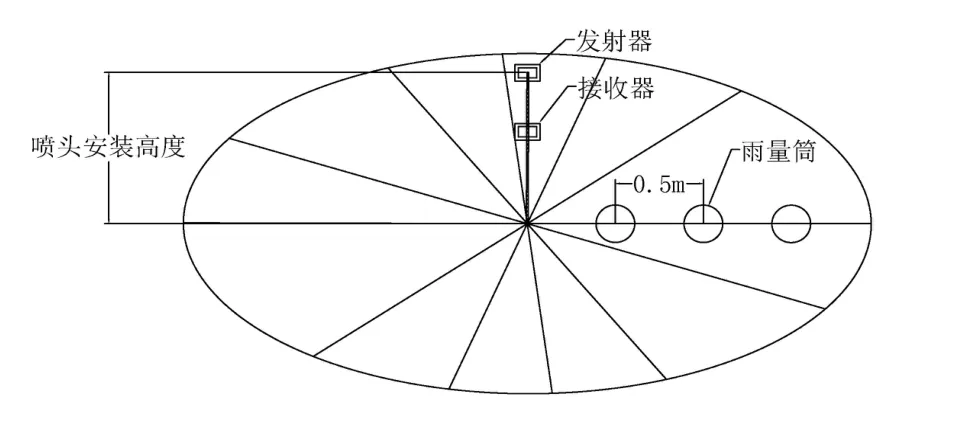
图3 雨量筒布置示意图Fig.3 Schematic diagram of rain gauge arrangement

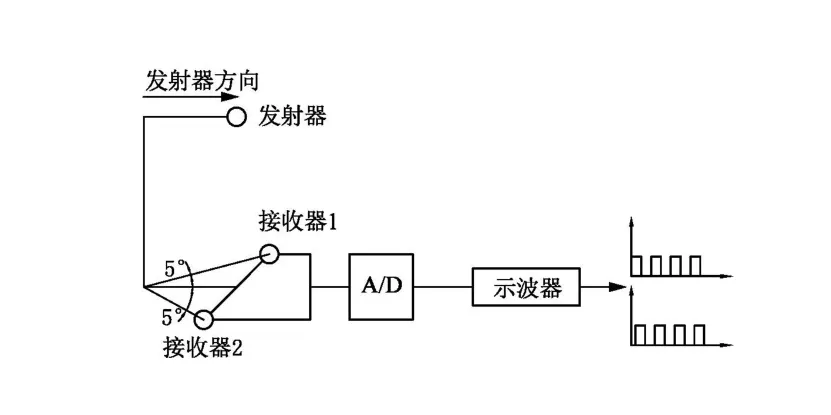
图4 旋转速度测量装置Fig.4 Rotation speed measuring device

1.2 射流元件及喷头工作原理

射流元件是射流式喷头完成步进旋转的关键部件。图5为射流元件结构简图。

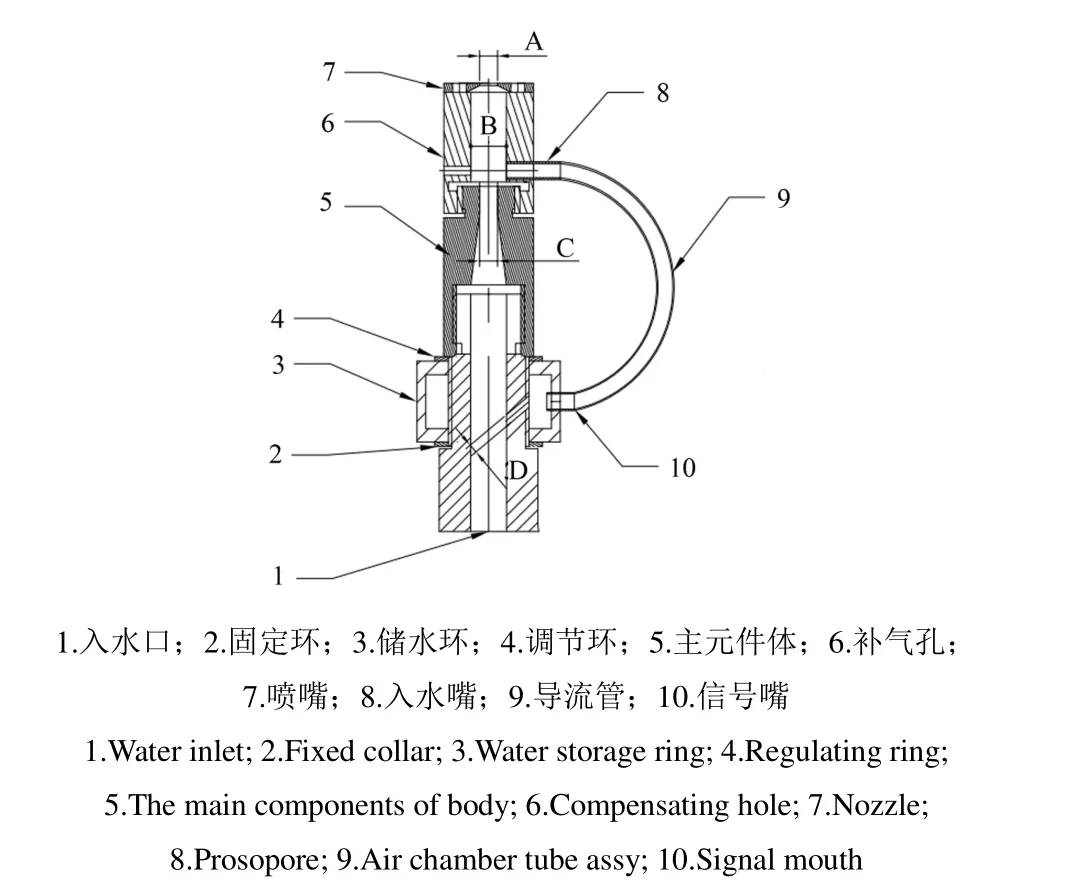
图5 射流式喷头射流元件Fig.5 Jet type nozzle jet element

射流式喷头的工作过程包括直射和附壁2个状态。图6（a）、图（b）所示为直射状态图，图6（c）、图（d）所示为附壁状态图。

直射状态：如图6（a）所示，射流元件左侧由补气孔补入空气，射流元件右侧由入水嘴上的导流管补入空气，因此主射流左右两侧的气压大小基本相等，主射流处于直射状态。

由图6（c）可知，信号水从管道流入入水嘴，射流元件右侧的导流管被信号水堵死，右侧无法补入空气，形成局部低压旋涡区，右侧压力低于左侧，射流向右侧附壁。

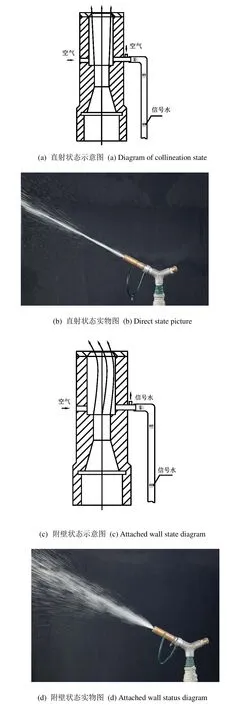
图6 喷头工作原理示意图Fig.6 Schematic diagram of nozzle working principle

1.3 全圆域水量分布计算方法

试验中布置的雨量筒测得的水深是喷头X轴方向上的径向水量分布，考虑到射流式喷头转速在全圆内并不均匀，因此1条射线上的水深并不能代表全圆域内喷头喷洒水量的空间分布。本文中设定有4条射线将喷洒域划分为4个象限Ⅰ、Ⅱ、Ⅲ、Ⅳ，表示其水量分布各不相同。全圆域水量分布计算算法流程如下：

1）通过样条插值计算喷头X轴方向上任意一点P的水量值，记X轴方向上的角度为θ。。

2）对喷洒域进行正方形网格划分，在划分过程中，由于随着网格数目不断增多，正方形网格的面积不断减少，因此，可以根据喷头不同工况下的射程设置足够多的网格节点数并将网格区域近似为一个点，通过该点的位置坐标计算网格区域的极坐标值。喷洒域内数值插值示意图如图7所示。

3）通过式（1）、极坐标夹角值θ和样条插值法计算喷洒域内各网格点的权值。

4）采用径向插值分别计算出各辐线上与喷头X轴方向上相同距离的水量hi。

5）喷头全圆喷洒域内任意点的水深即为Hi，其计算式为：

式中：A1为喷头灌溉过程中X轴方向上的旋转速度（rad/s）；P为喷头灌溉过程中在位置P的旋转速度（rad/s）；ri为网格P位置的权值。

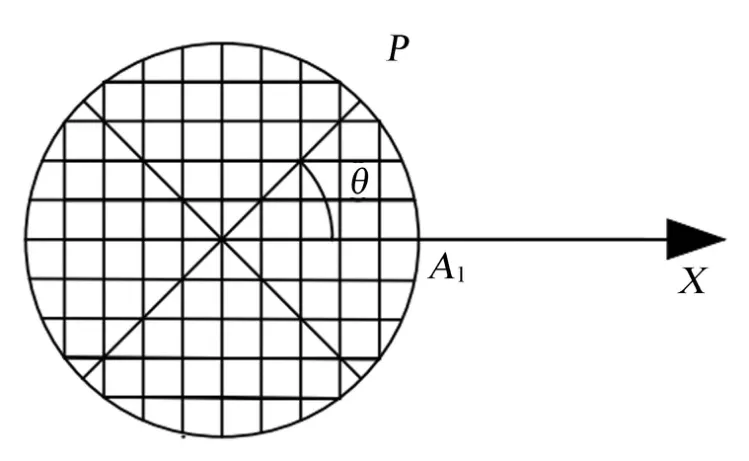
图7 喷洒域内数值插值示意图Fig.7 Schematic diagram of numerical interpolation in spraying field

1.4 喷灌均匀性评价模型

1）克里斯琴森均匀系数CU常用来评价喷头在喷灌面积上水量分布的均匀程度计算式[15-17]为：

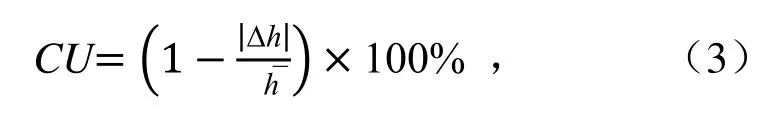
式中：CU为克里斯琴森均匀系数（%）；|∆h|为每一侧点喷洒水深的平均离差（mm）；为喷管面积上的平均喷洒水深（mm）。

2）分布均匀性系数是指部分测点水深的均值与总水深平均值的比值[18-19]，其计算式为：

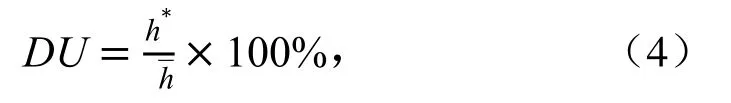
式中：h*为N/4个最小水深测点的平均值（mm）；¯h为喷灌面积上的平均喷灌水深（mm）。

3）变异系数CV用于表示各雨量筒水深的标准差与算术平均值的比值。喷灌均匀性越高，测得的变异系数越小。计算式[20-21]为：

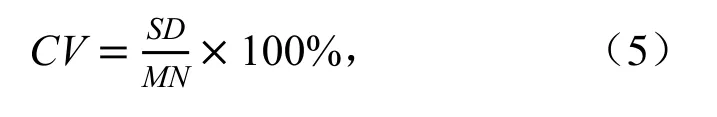
式中：CV为变异系数（%）；SD为所有雨量筒中水量的标准差（mm）；MN为所有雨量筒中水量的算术平均值（mm）。

2 结果与分析

2.1 喷灌强度局部变化规律

喷头单位时间的喷洒水深是评价喷头喷洒效果的重要特征参数。通过试验读取雨量筒采集的数据，得到了1.1、1.3、1.5 m安装高度和100、150、200、250、300 kPa工作压力下的径向水量分布曲线如图8所示。【从图8（b）、图（c）中可以看出，喷头在安装高度为1.3和1.5 m时，射程随着压力的加大而增长，在压力为100~150 kPa之间时，射程增长得很快，而后增速逐渐变缓，因为随着压力的不断增大，水滴的运动速度增大，水滴所受空气阻力变大，射流破碎的更充分，变成细小水滴，运动距离变近。安装高度为1.1 m时，射程随压力的增大变化相对均匀，这是由于水滴在空气中没有完全破碎的导致的】。如图8（a）、图（b）所示，安装高度为1.1、1.3 m，压力在150~300 kPa时，水量在距喷头初始位置2~8.5 m处分布均匀，而在喷洒末端一段距离内，水深急剧下降，说明喷头喷洒水柱破碎均匀，喷洒水滴直径及相应在同一数量级的频数成互相关趋势，相比单相流喷头其组合均匀性能更优越。安装高度为1.5 m时，水量在距喷头初始位置3~8.6 m处均匀分布，这是由于安装高度增高，降落在近处的水滴在空中运动时间加长运行距离会更远，且远处的水滴速度水平分量与垂直分量之间的夹角大，因而水滴运动距离变化并不是很明显。

2.2 压力-流量关系

射流式喷头在 1.3 m安装高度的流量测量值如表1所示。从表1可知，喷头的流量与压力呈正相关关系，随着喷头压力的增大，喷头的流量也随之增大。根据流体力学知识喷头流量与喷嘴直径以及工作压力的关系为：

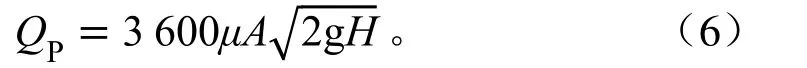
由此可得出流量系数的公式：

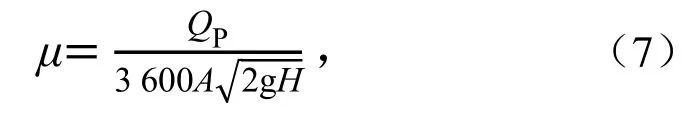
式中：QP表示喷头流量（m3/h）；μ表示流量系数；A表示喷嘴过流断面面积（m2）；H表示喷嘴出口压力，以米水柱表示（m）且1 m H2O=10 kPa。根据上式计算出该喷头的流量系数，可得到流量系数在0.545~0.585之间波动，随着压力的增大，流量系数呈先上升后下降趋势。

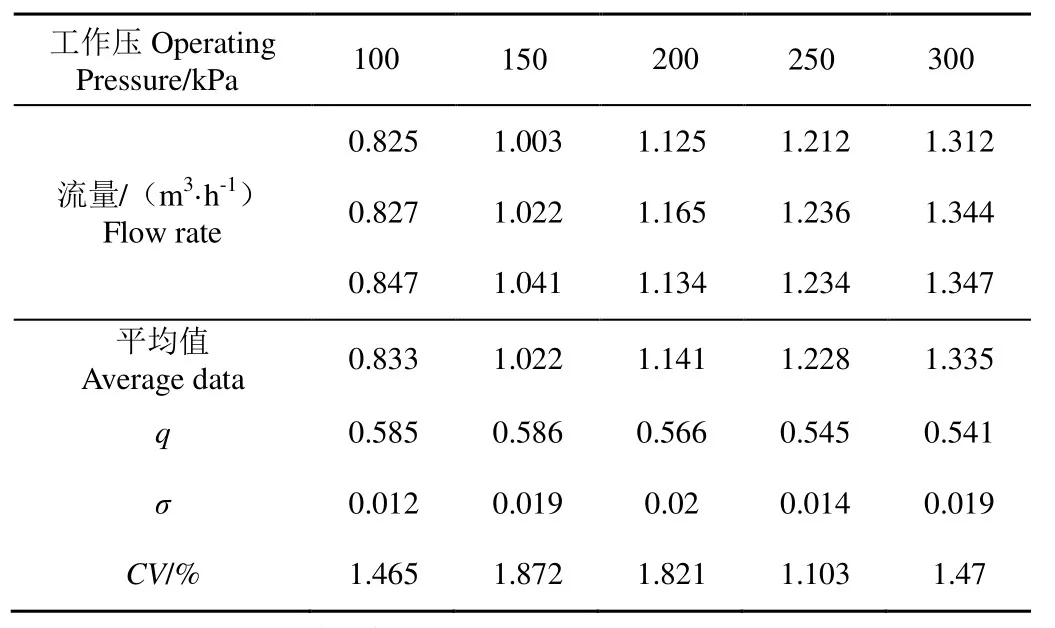
表1 压力-流量关系表Table 1 Pressure-flow relationship table

2.3 水量峰值局部变化规律

图9 为不同工作压力下水量峰值强度变化柱状图。从图9 可以看出，相同工作压力下，喷头在1.3 m安装高度时，水深峰值强度最大，当安装高度升高至1.5 m 时，水量峰值强度明显降低，工作压力为100 kPa，安装高度为1.1、1.3、1.5 m 时的水量峰值强度的对比分别为8.9、10.5、5.3。由此可见，喷头在压力为100 kPa、高度为1.1、1.3 m 时产生较大的喷灌水量峰值，易损伤作物，且破坏土壤结构，形成地表径流及冲蚀土壤，为喷头不利工况条件。相同安装高度下，灌溉水深峰值强度随着压力的增大呈现减小的趋势，但当压力增大到150 kPa 之后，减小的效果并不明显。这是由于随着压力的增大，喷头流量增大，已经开始弥补了水滴破碎而造成的灌溉水深强度减小的损失。当安装高度为1.5 m，工作压力分别为100、150、200、250、300 kPa 时，其水量峰值强度分别为5.3、5.1、4.9、4.7、4.9 mm/h，标准偏差（STD）为0.23 mm/h，说明此工况下喷灌水量峰值离散程度小，水量峰值集中5 mm/h 附近，适用于动压下进行喷灌。为探明安装高度为1.1、1.3 m 时，水量峰值强度与工作压力的非线性关系，本文利用MATLAB 软件，建立非线性数学建模型，回归出水量峰值强度与工作压力的变化函数为：

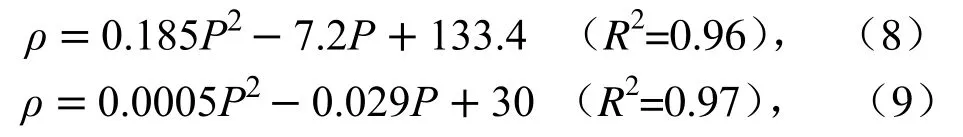
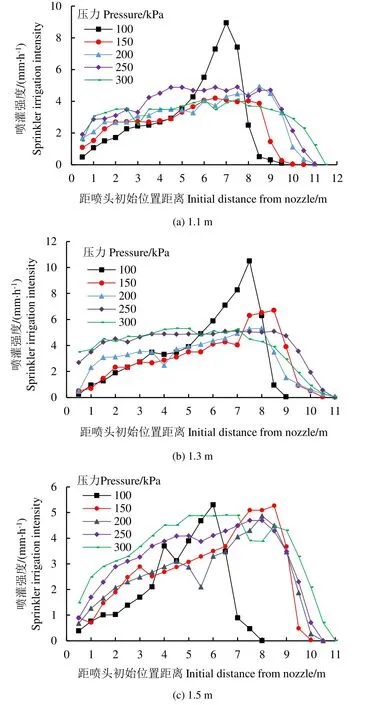
图8 不同工作压力下喷灌强度变化Fig.8 Variation of sprinkler strength under different working pressure

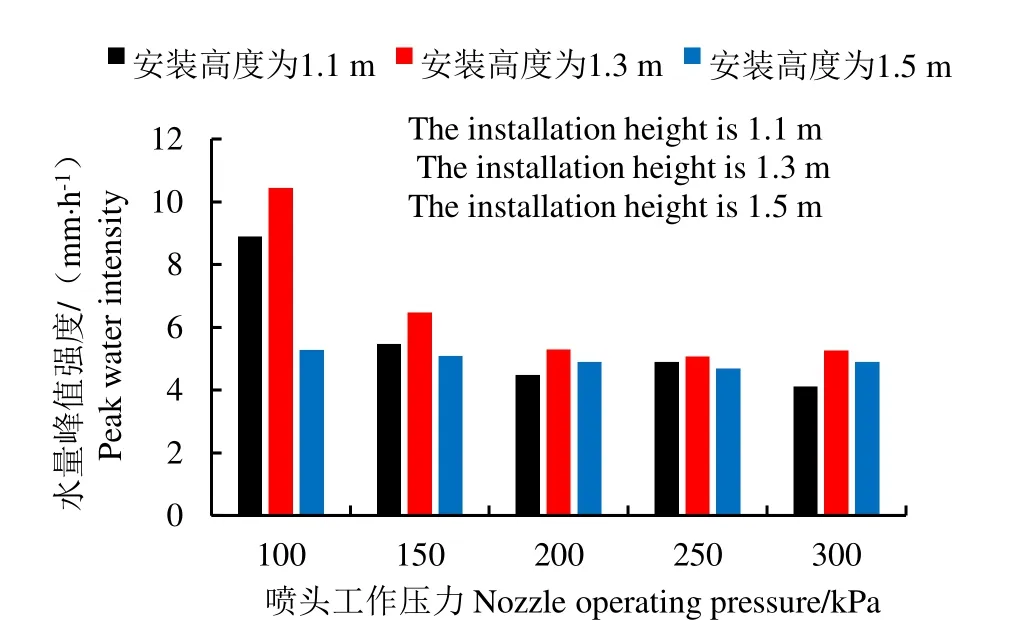
图9 不同安装高度下水量峰值强度变化Fig.9 Changes in peak water intensity at different installation heights

2.4 水量离散程度分析

从表2可以看出，喷头在1.1 m安装高度、100 kPa工作压力下CV最大，达到84%说明在该工况下水量分布最不均匀。增大工作压力，变异系数CV急剧下降。当增大喷灌压力，高速水柱截面不断扩大并逐步分成小水舌，水舌在重力、空气阻力和射流紊流的共同作用下快速破碎变形，在空气中破裂较为充分，产生许多细小的水滴，在一定范围内有利于提高水量的均匀分布。在工作压力为200 kPa，安装高度从1.1 m经1.3 m变化至1.5 m时，变异系数反而出现增大的趋势。这是由于随着高度的升高，距离喷头较近位置的水滴运动更远，在一定程度上造成了局部水量过于集中的现象。

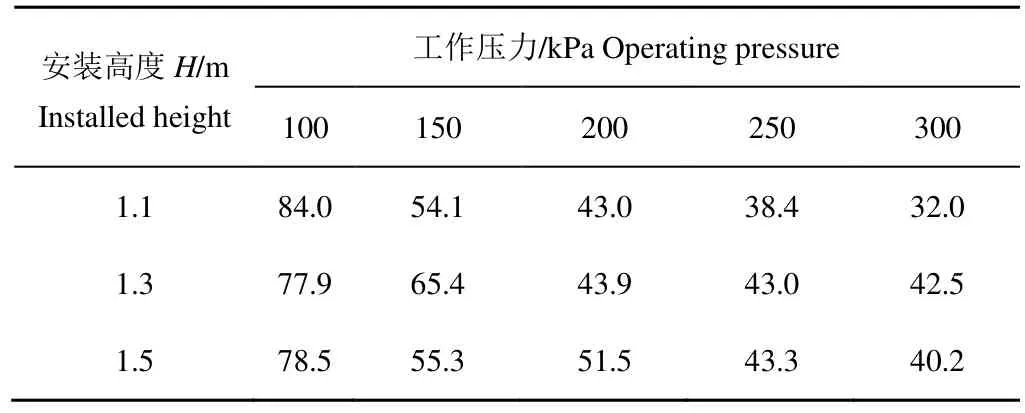
表2 不同工况下水量变异系数Table 2 Coefficient of water variation under different working conditions

表3 压力、安装高度-射程数值表Table 3 Pressure,mounting height-range table

2.5 压力、安装高度-射程关系

根据国家标准《旋转式喷头试验方法》中规定，射程是指喷头在无风条件下正常运行时，受水量雨筒中收集的水深为0.25 mm/h的点到喷头中心的水平距离。根据实测水量分布，首先确定试验数据中最后1次喷灌强度大于0.25 mm/h的水平距离，然后取该元素前3个后1个元素作为插值的“基准”数据；在利用3次样条插值所得的数据确定喷灌强度为0.25 mm/h的水平距离。对3次试验实测数据处理后，得到射流式喷头的射程如表3。

在表3所示的工况下，以喷头安装高度1.3 m，压力为100 kPa为例，分析工作压力与射程的关系结果如图10所示。由图10可知，当压力增至150 kPa时，射程增加15.26%；当压力增至200 kPa时，射程增加 18.74%；当压力增至 250 kPa时，射程增加20.99%；当压力增至300kPa时，射程增加19.98%。这说明喷头射程随着工作压力增大而增大，开始时增长得比较快，而后逐渐变缓，当达到一定极限时，随着压力继续增大，射程将不再增大。这是因为压力过大，水流的运动速度大，水滴受到空气阻力也增大，大粒径水滴在空气中不断发生二次破碎，变成粒径更小的水滴，飞行距离变近。

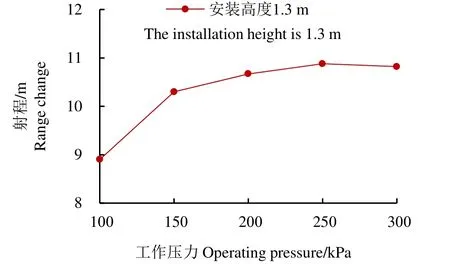
图10 安装高度为1.3 m 时工作压力与射程的关系Fig.10 Relationship between operating pressure and range at installation height of 1.3 m

以100 kPa为例，相比与安装高度1.1 m的射程，安装高度达到1.3 m的时候，射程减小2.9%；安装高度达到1.5 m的时候，射程减小14.59%。这说明随着喷头安装高度的增加，射程出现了下降的异常现象。在试验过程中发现在提升喷头安装高度时，压力调节器的位置并没有发生改变，安装高度增加的同时水流的沿程损失也在增加，喷嘴出口处实际压力稍微小。由于射流式喷头与全射流喷头的流道结构不同，随着压力的减小，出口水流扩散减小，水流更集中冲击出口壁面，驱动力增加使得喷头转速加快。因此，出现该异常现象的主要原因是喷头转速的加快。喷头在1.1、1.3、1.5 m安装高度的标准差及变异系数分别为0.09~0.15和 0.81~1.53、0.09~0.13和 0.78~1.22、0.06~0.14和0.51~1.36，数据波动幅度较小，表明喷头运转的稳定性高。

2.6 单喷头全圆域内水量空间分布

采用MATLAB对喷洒域内进行网格划分，通过3次样条插值方法求得任意网格点的降水深，得到了单喷头在 1.3 m 安装高度，100、150、200、250和300 kPa的工作压力下射流式喷头的空间水量分布，如图11所示。由图11可以看出，喷头在整个圆周内由于旋转速度的不一致，造成了局部水量过多的情形，从图11中局部水量过多的区域来看，在不同的工作压力下，喷头旋转速度最慢的区域主要分布在Ⅰ、Ⅳ象限。在100 kPa压力下，喷头4 m范围内仅存在2个梯度的相同颜色，此区域内旋转均匀性较好，当压力增大至200 kPa时，距喷头大概3 m处的圆环出现了断口，随后断口位置以喷头为中心不断向外扩张，且开口的角度也不断增大，随着压力升高至300 kPa时，断口位置已扩展至距喷头8 m处，且8 m范围内只有一个不规则的长条形圆环。从图11可知，随着工作压力的不断增大，靠近喷头近处的水量越来越多，当喷头压力达到250 kPa时，在喷头2 m外的3/4的圆域内灌水深高至4.5 mm/h，随后灌水深度为4 mm/h以上的已经占据大部分的喷灌区域。

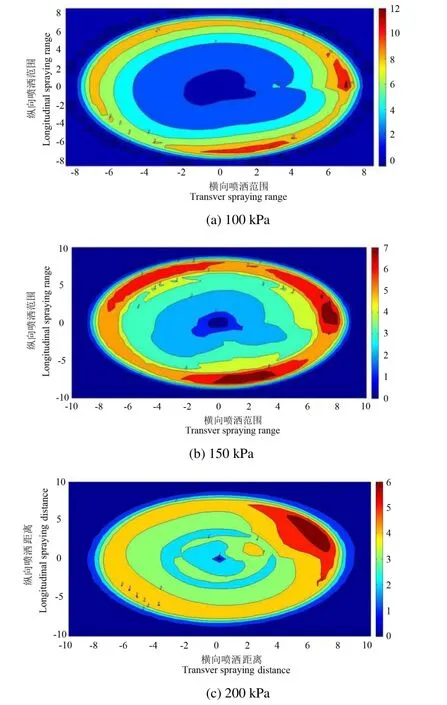
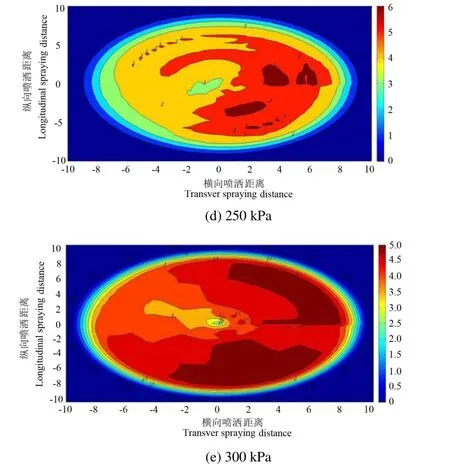
图11 1.3 m安装高度单喷头水量分布Fig.11 Water distribution at 1.3 m installation height of single sprinkler head

为评价在1.3 m安装高度下喷头水量分布的均匀性，分别计算了不同工作压力下整个喷洒空间范围内的DU和CU值的变化曲线，如图12所示。由图12可知，CU和DU的均值分别为64.82%、77.65%，标准偏差分别为0.155、0.093，CU的标准偏差超过DU的 2/3，这说明对评价喷灌水力性能的 2个指标CU和DU，压力对CU的影响更为明显，这与文献[28]的研究结论一致。喷头压力在100~250 kPa间，CU和DU的变化趋势基本一致，都随着喷头工作压力的增大而增大，当压力超过250 kPa时，DU继续增大而CU出现了减小的趋势，这说明CU和DU在不同的工作压力区间内并不都是简单的正相关关系，运用1stop软件分别对不同压力下的试验数据进行分析处理，得到CU、DU和压力P的函数关系式为：

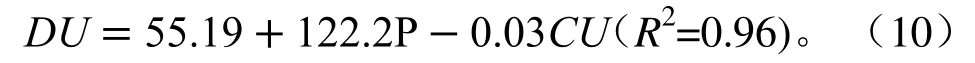
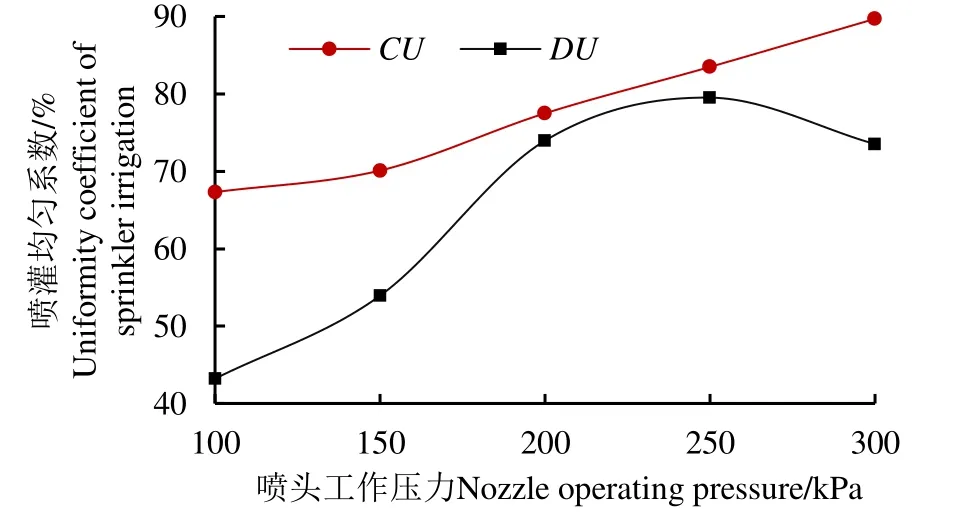
图12 1.3 m安装高度，不同工作压力下喷头的分布均匀性系数和克里斯琴均匀系数Fig.12 The values of DU and CU of the nozzle at 1.3 m installation height and under different operating pressures

2.7 组合喷头的空间水量分布

目前喷灌系统中喷头组合形式主要有正方形和三角形2种组合，采用对单喷头空间水量进行线性叠加的方法，得到喷头在1.3 m安装高度，250 kPa工作压力，0.8、1.0R和1.2R（R为喷头喷洒圆的半径）喷头间距下正方形和三角形组合的多喷头喷灌水量空间分布如图13所示，从图13可以看出，正方形组合的多喷头喷灌相当于单喷头全圆域喷洒的 4个象限分别布置在正方形的4个顶点，这使得喷灌区域内的水量分布近似对称，至于喷灌区域内水量分布不以矩形中心成完全对称，主要是由于喷头在4个象限内旋转的不均匀所造成。由图13可知，正方形组合形式的多喷头喷灌区域内喷灌强度峰值随着喷头间距的减小而逐渐增大，当喷头间距为0.8R时，喷灌强度峰值达到19 mm/h，相比1.2R的喷头间距增大了42%。0.8、1.2R的喷头间距按正方形组合喷洒范围内的喷灌强度峰值均要大于相同组合间距的三角形组合，从喷灌强度峰值指标考虑，选用0.8R和1.2R及其附近距离的喷头组合应尽量考虑三角形组合。1.0R的三角形组合的喷灌强度峰值大于所有的组合形式，其值高达20 mm/h,这说明实际喷灌系统中该喷头应避免采用靠近1.0R间距的三角形组合，以防止造成水土流失。

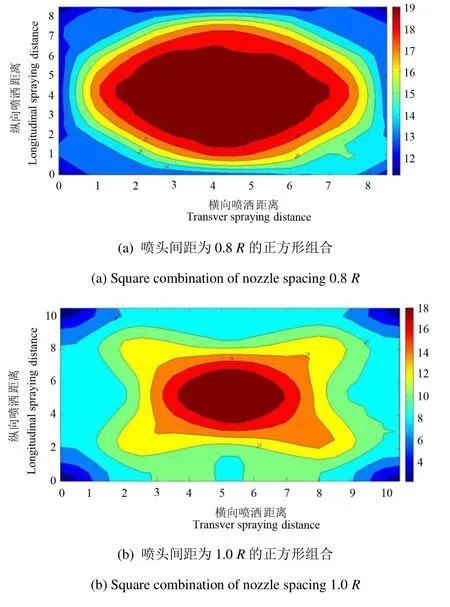
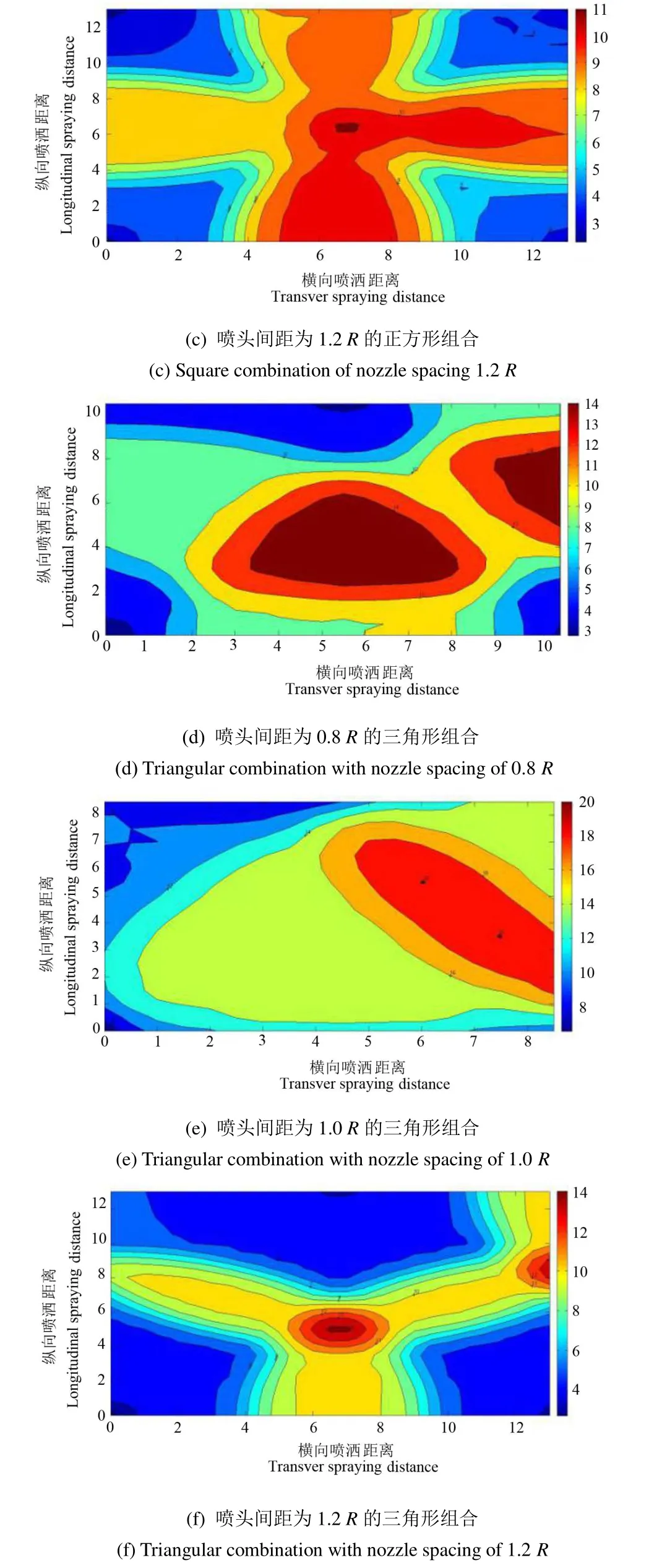
图13 0.8、1.0、1.2 R多喷头组合喷灌水量的空间分布Fig.13 Spatial distribution of water volume of 0.8 R,1.0 R and 1.2 R combined sprinkler irrigation

采用MATLAB对多喷头组合全喷洒域进行插值后，计算喷头在1.3 m安装高度，250 kPa工作压力，不同组合间距下的DU和CU值如图14、图15，由图14可知，喷头组合间距为5~7.5 m之间时，正方形和三角形组合的DU值基本在80%以上，相比相同安装高度和工作压力下单喷头的DU值增大10%左右，通过正方形和三角形的多喷头组合，在合理布置喷头组合间距下，能够避免田间水量分布灌水深度出现较小的情况，有利于保证作物获得必要的最小灌水量。由图14可知，正方形组合喷灌的CU值总体上随喷头间距的减小呈下降趋势，组合后的最大值出现在喷头5.25 m（0.5R）间距时，CU为98.6%；喷头间距11.55 m（1.1R）时，CU最低76.4%，对CU趋势进行拟合得到CU与喷头组合间距存在指数函数关系，其函数关系式为：

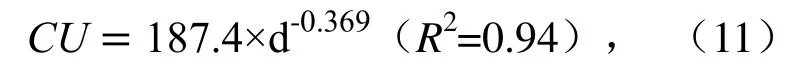
从图15中三角形组合喷灌的CU变化曲线可知，喷头间距在8~11.5 m之间，CU总体呈下降趋势，在喷头间距为12 m时，CU降至67.2%。将8种不同组合间距下的CU值进一步分析，建立三角形组合下喷头间距与CU值关系的数学模型，函数关系式为：

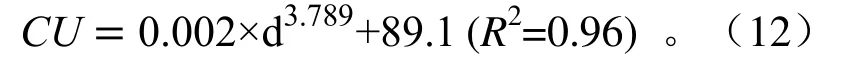
对不同组合间距下CU的预测模型式进一步分析，射流式喷头为达到喷灌工程规范中规定的行喷灌均匀度85%，在实际喷灌工程中正方形组合喷灌的间距应小于8 m，三角形组合喷头之间的间距布置在8 m附近。

图14 正方形组合喷灌的 DU 和 CU 值Fig.14 Square combination of DU and CU for sprinkler

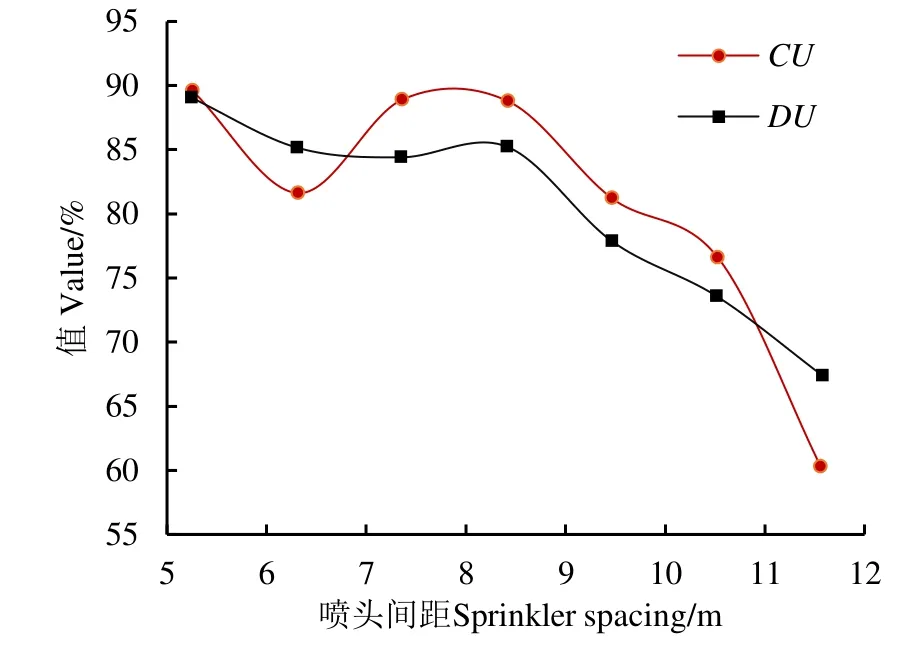
图15 三角形组合喷灌的DU 和CU 值Fig.15 The triangle combines DU and CU values for sprinkler irrigation

3 结 论

1）喷灌强度、水量峰值与喷头的安装高度及工作压力有关。随着安装高度的升高，工作压力的增大，水滴在空气中破碎越充分，喷灌强度在径向方向上分布越均匀。在喷头喷洒末端的一定距离，喷灌强度急剧下降，因而有利于提高该喷头组合喷灌水量分布的均匀度。

2）针对100 kPa下水量峰值强度过高的情形，回归出1.1、1.3与1.5 m喷头安装高度，100~300 kPa压力区间的水量峰值强度的预测模型。在实际喷灌作业中应当避免因水量峰值过大从而形成的地表径流。

3）射流式喷头在Ⅰ、Ⅳ象限内旋转接触部位摩擦力相对过大，引起了单喷头喷灌水量分布在此区域内水量集中的情况。在不同的工作压力下，单喷头分布均匀性系数CU比喷灌均匀性系数DU变化更为明显，且DU与CU呈负相关关系。

4）建立了多喷头组合喷灌水量分布DU、CU与喷头间距d的计算模型，拟合均匀系数在0.94以上。喷头间距在7~8.5 m之间时，正方形组合喷灌的DU和CU值均达到喷灌工程规范中规定的行喷灌均匀度；喷头间距在5.25~11.55 m之间时，三角形组合喷灌均匀性要优于正方形组合。