同类相食对具有密度制约项种群模型的动力学影响

蔺小林， 刘宗英， 朱 雪， 李建全

(陕西科技大学 文理学院， 陕西 西安 710021)

0 引言

近年来，人们发现同类相食现象是许多种群共有的自然现象.Bazazi S等[1]研究了沙漠蝗虫在大规模迁移中受到同类相食行为的影响；Carl Smith等[2]研究了硬骨鱼类间存在的同类相食现象；Gabriel和Bosch提出了同类相食具有调节生态规模的潜力，同时对物种的生存具有稳定调节作用[3-5].

在生态环境中，几乎所有的种群生长都具有阶段结构，阶段结构模型更能表现出物种复杂的动力学性态[6-9].在1990年，Aiello和Freedman[10]讨论了一类具有幼年和成年两个阶段的种群增长模型，得到了系统正平衡点全局稳定的充分条件.陈兰荪和王东达曾系统地介绍了具有阶段结构种群的动力学模型的一些研究成果[11].Kang等[12]对于卵会被成熟个体所吞噬的同类捕食模型进行了研究：

发现了此类同类相食行为会促进种群个体内部的平衡，即种群存活平衡点的稳定性[12].因此，将同类相食考虑到阶段结构模型中具有重要的现实和实际意义[13-15].

本文在Kang等[12]提出模型的基础上，假设同类相食发生于种群成长阶段的幼虫和成虫之间，即成虫会因存活需要而捕杀幼虫，以降低成虫的死亡率，考虑到成虫具有密度制约项[16]，在实际中常认为成虫之间存在种内竞争和资源竞争，从而成虫的死亡率比较快，即死亡率应遵循logistic型.同时幼虫的死亡来自于自然死亡和成虫的捕杀两个方面，建立一类具有两阶段结构的同类相食模型.

1 模型及正不变集

本文讨论以下具有两阶段结构(幼年种群、成年种群)的同类相食模型：

(1)

其中J(t),A(t)分别表示t时刻幼年种群、成年种群的数量，b为不存在幼年种群制约情形下每个成年种群的繁殖率，α为单个成年种群对幼年种群的捕获率，μ1为单个幼年种群的自然死亡率，β为幼年向成年种群的转化率，μ2为单个成年种群在不捕杀幼年种群情形下的死亡率，ε1为幼年种群对其出生率的制约系数，ε2为成年种群捕杀幼年种群后自身死亡率减少的系数，δ表示密度制约下成年个体的死亡率系数.除α,ε2外，其它所有参数都为正数.当α>0,ε2>0时，表示成虫会对幼虫进行捕杀；当α=ε2=0 时，表示没有同类相食行为，模型变为

(2)

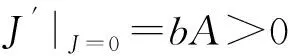
其次，由模型(1)的第一个方程得

其中

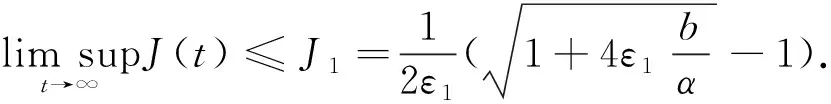
这意味着对于任意小的ε>0,存在T>0,使得当t>T时JT时，由模型(1)的第二个方程有

其中

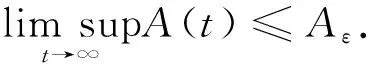
因此，区域D1={(J,A):0≤J≤J1,0≤A≤A1}为模型(1)的一个正不变集，其中

对于模型(2)

因此，区域

是模型(2)的一个正不变集.

2 无同类相食时模型(2)的动力学性态分析

本节分析无同类相食情形下(即α=ε2=0)模型(1)的动力学性态，对模型(2)直接求解方程组

(3)

可得方程组(3)的正解即对应模型(2)的平衡点.

由模型(2)的第一个方程可得

(4)

当J≠0时，将上式代入到模型(2)的第二个方程可得

(5)

再将方程(4)代入到上式可得

即

(μ1+β)[(μ1+β)(1+ε1J)δJ+μ2b].

由F(J)直接计算可得

F(0)=b[βb-μ2(μ1+β)].

因此，总结以上推理，关于模型(2)平衡点的存在性有如下叙述.

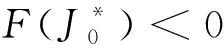
关于模型(2)平衡点的局部稳定性有：

定理2 对于模型(2)，种群灭绝平衡点O(0,0),当βb≤μ2(μ1+β)时，在集合D2内是局部渐近稳定的，当βb>μ2(μ1+β)时是不稳定的.种群存活平衡点E0(J0,A0)只要存在，在集合D2内就一定是局部渐近稳定的.

证明：由模型(2)在O(0,0)处的Jacobi矩阵可知，平衡点O(0,0)当βb<μ2(μ1+β)时是稳定的，当βb>μ2(μ1+β)时是不稳定的，当βb=μ2(μ1+β)时是高阶奇点.

为了分析平衡点O(0,0)当βb=μ2(μ1+β)时在区域D2上的稳定性，做变换

(6)

则模型(2)可变为

(7)

其中

X=β(μ22ε1+δβ);Y=μ2(βε1b-μ22ε1-2δβ);

Z=μ2β2(δ-ε1b);W=β(μ22bε1-βb2ε1-2μ22δ).

系统(7)的线性部分满足局部中心流形存在的条件，因此设系统(7)在原点的局部中心流形为v=h(u)=au2+o(u3)对它两边关于t求导得v′=[2au+o(u2)]u′并结合系统(7)可得

将上式代入系统(7)的第一个方程，得到中心流形上的解满足

由上式的第一项次数为偶数可得，O(0,0)是系统(7)的鞍结点.进一步，根据变换(6)可知，O(0,0)在集合D2上是局部渐近稳定的.

综上所述，当βb≤μ2(μ1+β)时，平衡点O(0,0)在集合D2上是局部渐近稳定的.

模型(2)在E0(J0,A0)处的Jacobi矩阵为

利用J0和A0满足的方程组(3)，可得

于是

由方程(5)可得

(μ1+β)(μ2+δA0).

将方程(4)代入上式，进一步可得

(μ1+β)(μ2+δA0)=(μ1+β)(μ2+δA0)

因此，平衡点E0(J0,A0)只要存在，就一定在集合D2内是局部渐近稳定的.

定理3 种群灭绝平衡点O(0,0)在集合D2内全局渐近稳定；平衡点E0(J0,A0)只要存在，就一定在集合D2内是全局渐近稳定的.

证明：为了证明种群灭绝平衡点O(0,0)在D2上的全局稳定性，定义Lyapunov函数为L1=βJ+(μ1+β)A,则L1沿着模型(2)的解的全导数为

为了证明种群存活平衡点E0(J0,A0)存在时的全局稳定性，首先将模型(2)变形为

(8)

其次，定义关于E0(J0,A0)的Lyapunov正定函数

则函数L2沿着系统(8)的全导数为

由方程(4)和(5)可得

则有

(μ2+δA)(A-A0)]2≤0.

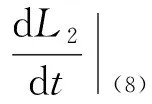
3 具有同类相食时模型(1)的动力学性态分析

本节分析同类相食存在时，即α,ε2≠0时种群平衡点的存在性和稳定性，模型(1)总存在种群灭绝平衡点O(0,0).为了确定模型(1)的种群存在平衡点，令模型(1) 的左边为零，得到

(9)

方程组(9)的正解即对应模型(1)的种群存在平衡点.

由方程组(9)的第一个方程可以得到

(10)

其中b-αJ(1+ε1J)>0,当J≠0时，将上式代入方程组(9)的第二个方程有

(11)

将式(10)代入方程(11)可得

记

根据模型(1)有正不变集D1，G(J)=0在(0,J1)上的零点对应模型(1)正平衡点J的坐标.于是，可通过判定方程G(J)=0在区间(0,J1)上根的存在性得到模型(1)正平衡点的存在性.其中，

G(0)=μ2(μ1+β)-βb,

对函数G(J)求导可得

G″(J)=

并且对于函数G(J)有

于是关于方程G(J)=0正根存在性讨论如下：

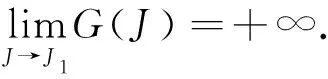
当ε1<ε2时，G″(J)>0 ,即函数G(J)的图形是上凹的.于是若G(0)<0或G(0)=0且G′(0)<0,则函数G(J)在区间(0,J1)上也有唯一零点.注意到G(0)=0,即μ2(μ1+β)=βb时，

注意到

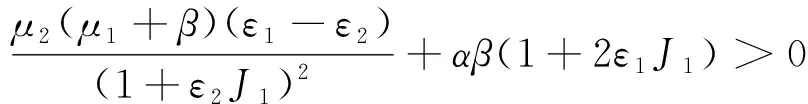
因此，总结以上推理，关于方程G(J)=0在区间(0,J1)上平衡点的存在情形有如下定理：

定理4 当下列条件之一满足时，模型(1)在区域D1内有唯一的正平衡点E*(J*,A*),

(i)μ2(μ1+β)<βb;(ii)μ2(μ1+β)=βb

且μ22[b(ε2-ε1)-α]>βbδ.

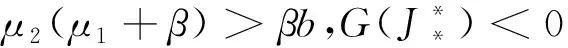
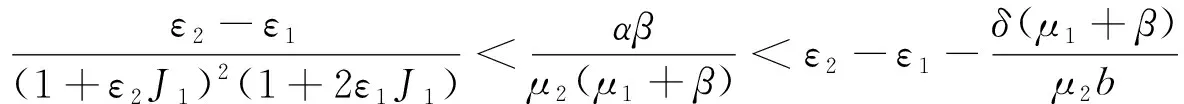
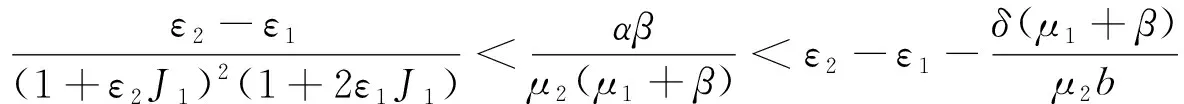
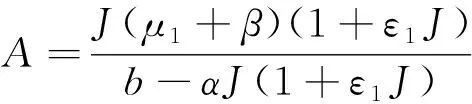
根据定理4的推理过程，对其做下面四点注：

注1 (1)对于定理4中模型(1)在区域D1内有唯一的正平衡点E*(J*,A*),其满足G′(E*)>0.

(3)对于定理4中模型(1)在区域D1内有两个正平衡点E*(J*,A*)和E*(J*,A*).

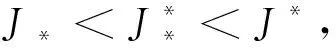
(4)由于G′(0)<0意味着ε1<ε2,因此定理4(ii)、(iii)以及模型(1)存在两个正平衡点的条件中均未明确写出条件ε1<ε2.

关于模型(1)平衡点局部稳定性有如下结论：

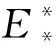
证明：模型(1)在O(0,0)处的Jacobi 矩阵为

因此，对于矩阵M(O)当βb<μ2(μ1+β)时,平衡点O(0,0)是稳定的；当βb>μ2(μ1+β)时，平衡点O(0,0)是不稳定的；当βb=μ2(μ1+β)时，平衡点O(0,0)是高阶奇点.

当βb=μ2(μ1+β)时，做变换

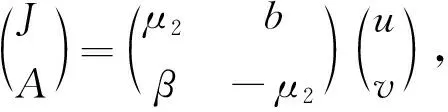
(12)

其中

A=(βb-μ22)[b(ε2-ε1)-α]+2βbδ,

B=μ22[b(ε2-ε1)-α+δ],

C=(βb-μ22)[β(bε1+α)+ε2μ22]+2μ22δβ,

D=b[β(bε1+α)+ε2μ22]+μ22δ.

根据中心流形定理[19]，可求得系统(12)在原点的局部中心流形为

o(u3).

进一步将上式代入系统(12)中的第一个方程得

(13)

根据式(12)和(13)可得，当μ22[b(ε2-ε1)-α]≠βbδ时，原点为系统(12)的鞍结点.如果μ22[b(ε2-ε1)-α]<βbδ,则系统(12)在u>0一侧原点渐近稳定；如果μ22[b(ε2-ε1)-α]>βbδ,则系统(12)在u>0一侧为鞍点情形，是不稳定的.当μ22[(bε2-ε1)-α]=βbδ时，式(13)变为

因此，当μ22[b(ε2-ε1)-α]=βbδ时,O是渐近稳定的.

综上所述，当μ2(μ1+ε)>βb或μ2(μ1+β)=βb且μ22[b(ε2-ε1)-α]≤βbδ时，模型(1)的种群绝灭平衡点O(0,0)是渐近稳定的；当μ2(μ1+ε)<βb或μ2(μ1+ε)=βb且μ22[b(ε2-ε1)-α]>βbδ时是不稳定的.

下面讨论模型(1)正平衡点的稳定性：

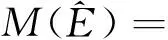
(14)

计算可得

由方程(9)的第一个方程可得

由方程(9)的第二个方程可得

因此

利用式(11)可得

将式(10)代入上式可得

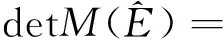
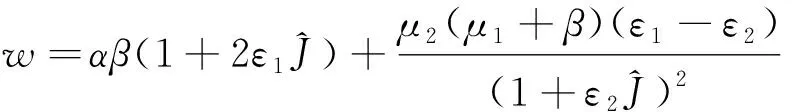
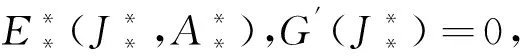
(15)

系统(15)在其原点附近可表示为

(16)

再对系统(16)做变换

可得

(17)

其中

类似于种群灭绝平衡点O当βb=μ2(μ1+β)时的讨论，系统(17)在其过原点的中心流形退化为

对于模型(1)，记

因此模型(1)在区域D1内无闭轨线.进一步，由于模型(1)的正不变集D1的有界性，根据前面得到的其平衡点的局部稳定性，关于模型(1)的全局动力学有如下定理：

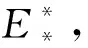
为了更直观地显示模型(1)的全局动力学性态，下面对幼年种群J(t)与成年种群A(t)进行数值模拟：

(1)取参数为β=0.3,b=0.9,μ1=0.7,μ2=0.4,ε1=0.01,ε2=0.02,α=0.25,δ=0.1, 此时，μ2(μ1+β)>βb, 因此模型(1)的种群灭绝平衡点O是全局渐近稳定的(如图1所示).

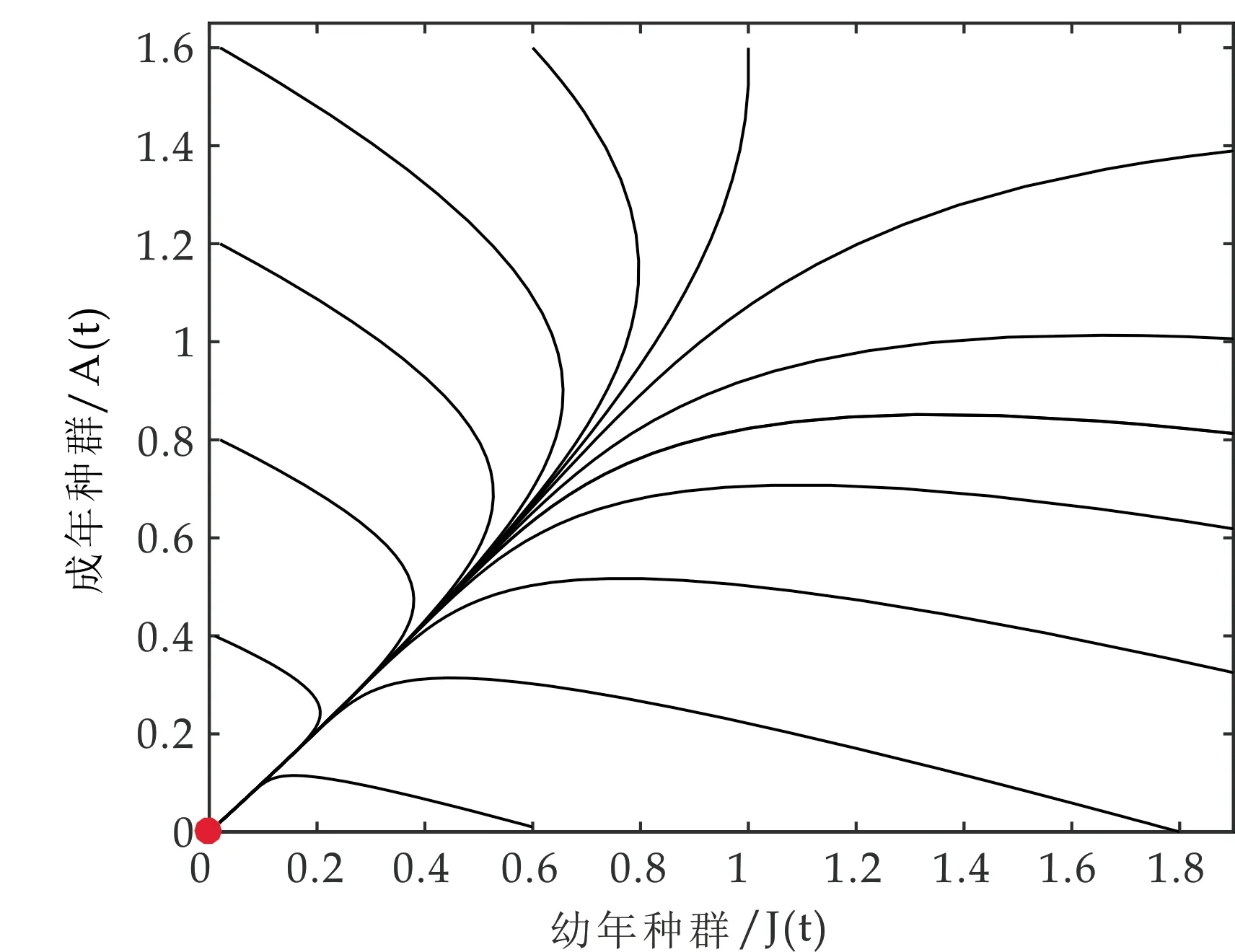
图1 当μ2(μ1+β)>βb时，种群灭绝平衡点O全局渐近稳定

(2)取参数为β=0.3,b=0.8,μ1=0.3,μ2=0.3,ε1=0.01,ε2=1.5,α=0.05,δ=0.15, 此时，μ2(μ1+β)<βb，模型(1)有唯一的种群存活平衡点E*(2.027,1.781).该平衡点E*是全局渐近稳定的(如图2所示).

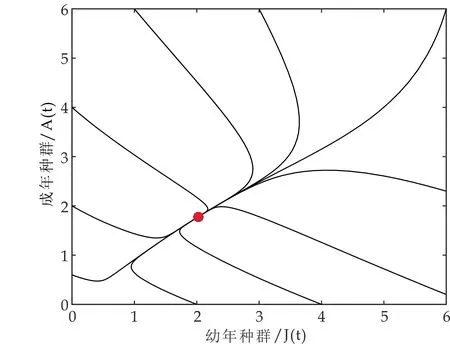
图2 当μ2(μ1+β)<βb时，种群唯一存活平衡点E*全局渐近稳定

(3)取参数为β=0.300 01,b=0.379 99,μ1=0.3,μ2=0.3,ε1=0.01,ε2=0.52,α=0.035 59,δ=0.001 001, 此时有下列条件成立,

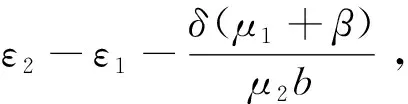
取另一组参数如下β=0.3,b=0.412,μ1=0.3,μ2=0.3,ε1=0.01,ε2=0.501,α=0.05,δ=0.001此时，

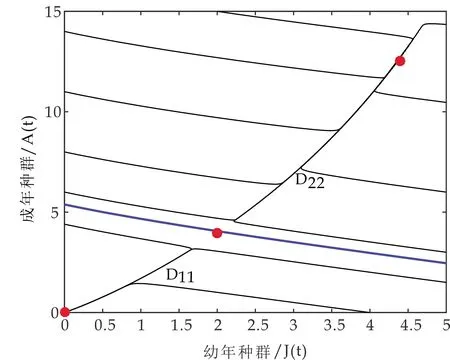
(a)模型(1)存在两个存活平衡点时的轨线图

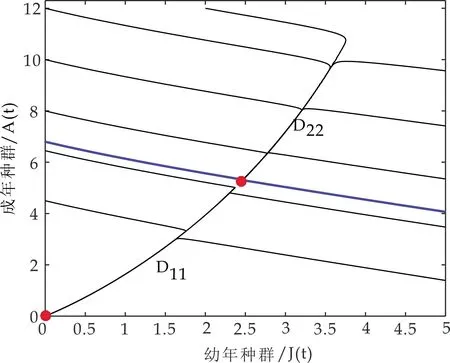
(b)模型(1)存在唯一存活平衡点是鞍结点时的轨线图图3 模型(1)的全局动力学性态图

4 结论

本文假定成年个体会对幼年个体进行同类捕食，并考虑在幼年个体的自然死亡和成年个体的密度制约项的基础上，建立了一类具有两阶段结构的同类相食模型.分析了模型平衡点的存在性和稳定性.对不具有同类相食行为的，通过构造适当的Lyapunov函数证明了平衡点在一定条件下的全局稳定性.

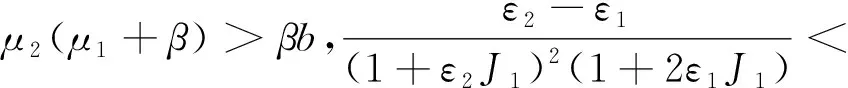
这些结果的得到有利于人们合理地控制有关种群的成长，对保护有关种群结构有着重大影响.因此同类相食行为在种群模型结构中具有重要作用.