基于Simulink的延伸喷管燃气展开过程联合仿真*

陈 鹏，宋学宇，曹涛锋，尤军峰

(1.中国航天科技集团公司四院四十一所，西安 710025；2.固体火箭发动机燃烧、热结构与内流场国防科技重点实验室，西安 710025；3.西北工业大学 航天学院，西安 710072)

0 引言

延伸喷管技术是提高固体火箭发动机性能的关键技术之一。对于采用作动筒推动方式展开的延伸喷管，作动筒展开力是决定延伸喷管动力学特性的关键因素。作动筒的展开方式包括燃气式、气瓶式、产气式等。

采用燃气发生器提供展开力的展开方式属于产气式，通过燃气发生器燃烧室内固体药柱的燃烧，产生大量高温高压的气体，经滤网与管路进入作动筒内，推动延伸喷管展开。整个点火展开过程包括点火-燃烧-传递-做功-展开五个步骤，且气体在作动筒内的展开做功过程(下游)对燃烧室内药柱燃烧(上游)存在影响，为了对延伸喷管展开进行准确预示，必须要对整个点火展开过程进行完整建模分析。

现有的仿真计算局限于单系统的建模仿真，如燃气发生器的内弹道仿真计算，气体充压过程仿真计算[5]，延伸喷管展开动力学、展开碰撞、燃气尾流仿真计算[6-11]等。但由于燃气发生器内弹道参数与下游过程相关，且受延伸喷管展开系统机构的影响，下游气体做功过程无法通过简单试验模拟，必须联合整个点火展开系统进行试验，周期较长且成本较高。在喷管外载荷不确定，且展开机构受加工工艺影响较大的条件下，仅通过单个系统的仿真计算，无法给出药柱与展开动力学参数的关系。而如何确定燃气发生器药形与药量，是在工程实际中必须予以解决的问题。

针对作动筒式双级延伸喷管采用燃气发生器展开的工况，本文通过在Matlab/Simulink中构建燃气发生器药柱燃烧与作动筒内燃气的膨胀做功模型，结合Ansys的动力学仿真模块，对从燃气发生器点火开始的延伸喷管展开全过程进行联合仿真，以期在燃气发生器药型与药量发生变化时，可以对延伸喷管展开过程进行预测。通过与已有试验测试数据的对比，验证仿真结果的准确性，建立完整可靠的延伸喷管点火展开模型。

1 燃气展开模型

在延伸喷管的展开过程中，作动筒的充气过程从燃气发生器点火开始。不计点火时间，主装药开始燃烧并产生高焓值的气体，经过滤网后进入管路，最终进入作动筒并膨胀做功，推动作动筒展开，带动延伸喷管展开到位。通过建立药柱燃烧及燃气膨胀做功的模型，可以为延伸喷管动力学模型提供输入条件，再经动力学仿真，最终得到延伸喷管展开的动力学参数。

1.1 燃烧过程

由维耶里模型可知，燃速rc与燃烧室内压pc的关系为

rc=a0pcn

(1)

由于药柱采用内孔+端面燃烧的方式，且由多个药片组合成，单个药片形状如图1所示。

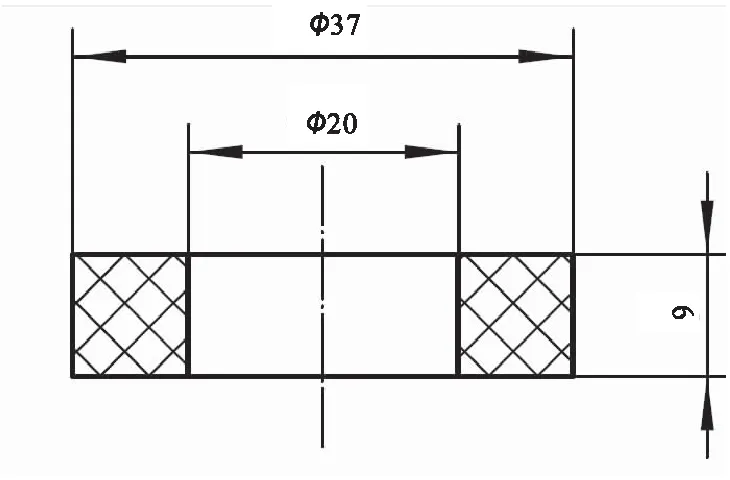
图1 药片尺寸图Fig.1 Size of the charge pellet

故燃面Ab为

Ab=2π[D2-(d+2rct)2]/4+

π(d+2rct)(h-2rct)

(2)

(3)

由质量守恒可知，药柱燃烧减少的质量，一部分成为残渣被滤网阻拦，一部分作为燃气进入作动筒内膨胀做功，则有

(4)

受过滤网与气体管路影响，燃气发生器燃烧室内压与作动筒内压不一致，但两者间存在一定的关系。一般来说，可建立起作动筒内压pzdt(因变量)相对于燃气发生器内压pc、时间t(自变量)的单值函数关系。但由于试验条件限制，燃气发生器内压无法测量，只能由试验数据近似建立燃气发生器内压pc(因变量)相对于作动筒内压pzdt(自变量)的函数关系如下：

pc=k1pzdtek2pzdt

(5)

注意到此关系内不含时间项t，且对于同一个燃烧室内压pc可能对应不同的作动筒内压pzdt。

1.2 膨胀做功过程

理想气体方程:

(6)

结合质量守恒方程，有

(7)

开口系统能量守恒方程:

(8)

由于每个燃气发生器为2个作动筒供气，有

(9)

1.3 动力学展开过程

延伸喷管展开的动力直接来源于作动筒内的高压气体。因此，对于延伸喷管，作动筒内压产生的推力是运动输入，各运动部件的位移、速度、加速度等动力学参数是运动输出。

展开阻力来源有三部分：(1)作动筒展开内部阻力，由预紧力产生的摩擦力与展开过程中筒间正压力产生的摩擦力两部分组成；(2)展开即将到位时产生的阻力，由延伸锥侧向密封圈摩擦力、延伸锥端面密封圈阻力、折转片到位后的拉力三部分组成；(3)热试中尾部燃气对延伸锥产生的作用力，根据燃气不同的膨胀状态，可能产生引射力或者阻力，其值可由流场计算得到。

由展开过程可知，作动筒容积Vzdt，与作动筒上端沿作动筒展开方向的位移szdt关系为

Vzdt=V0+Azdtszdt

(10)

由运动关系可知：

(11)

在喷管展开方向(轴向)上，作动筒内压(考虑作动筒内摩擦fzdt)的分量克服轴向摩擦力ff、尾部燃气阻力Fe使喷管展开。由于展开机构限制，延伸喷管I(下标1)、II(下标2)级之间的位移关系固定为1∶2，故在轴向有

(pzdtAzdt-fzdt)szdt=(ff1/2+ff2+Fe1/2+Fe2)sysz+Ek

(12)

式中sysz为II级延伸锥位移；Ek为动能项，展开到位后动量为0。

不考虑碰撞损失，延伸锥展开到位后，作动筒内燃气做功完全用来克服摩擦力及尾部燃气阻力。

文献中对延伸喷管的动力学展开进行了理论分析。但针对双级延伸喷管，在不大量简化模型的情况下，直接通过微分方程进行理论计算是非常复杂的。为了更加详细的反应模型参数，采用多体动力学仿真软件Ansys对延伸喷管展开模型进行建模分析。

2 Ansys多体动力学模型

在Ansys中对1/4延伸喷管进行建模，给定作动筒上的摩擦阻力、到位等效阻力以及燃气对延伸锥的作用力，以作动筒内压作为输入量，输出作动筒上端在作动筒展开方向上的的速度和加速度。三维模型如图2所示。

图2 延伸喷管1/4模型Fig.2 Quarter model of the extendible nozzle

在模型中，作动筒阻力通过设置作动筒上的预紧力和摩擦系数给出；延伸锥展开到位阻力的产生包含了与密封圈摩擦和碰撞过程，模型中采用近似曲线进行模拟，图3中纵轴为延伸锥展开到位阻力(等效在II级延伸锥上)，横轴为II级延伸锥质心轴向坐标。亦可采用显式动力学计算出阻力随展开位移变化曲线，作为参数输入模型中；尾部燃气产生的阻力与发动机工作状态以及延伸喷管展开位置有关，在发动机工作状态稳定的情况下，采用流场计算得到尾部燃气阻力随延伸锥展开位移的变化曲线，并作为参数输入模型中。图4中纵轴为两级延伸锥所受的燃气阻力，横轴为II级延伸锥质心轴向坐标。

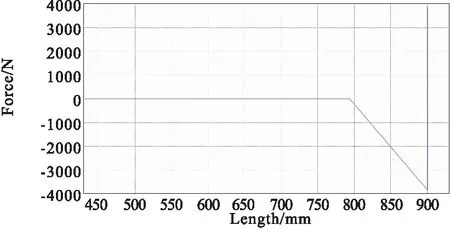
图3 延伸锥展开到位阻力曲线Fig.3 Mechanical resistance of the extendible nozzle

图4 喷管燃气阻力曲线Fig.4 Gas resistance of the extendible nozzle

为模拟棘轮式折转片的锁紧过程，防止仿真中展开到位后延伸锥回弹，在折转片、插销上定义接触，并减小计算步长。仿真中发现，棘轮式转动锁紧机构可以相当可靠地保证锁紧，即使未展开至预定的最终位置，也可防止延伸锥在外力作用下回弹。

在动力学模型建立完成后，通过输入实测的作动筒内压曲线，可较为准确地仿真出延伸锥展开曲线，如图5所示；若给出期望的展开位移曲线，也可计算出需求的作动筒内压曲线。即作动筒内压曲线与延伸锥展开曲线之间的动力学模型是完整可靠的。但如果燃气发生器药量发生改变，很难通过对内压曲线的线性变化来准确预示新的展开曲线，必须结合燃气发生器内部的燃烧与燃气膨胀做功的过程进行求解，进行多系统的联合仿真。

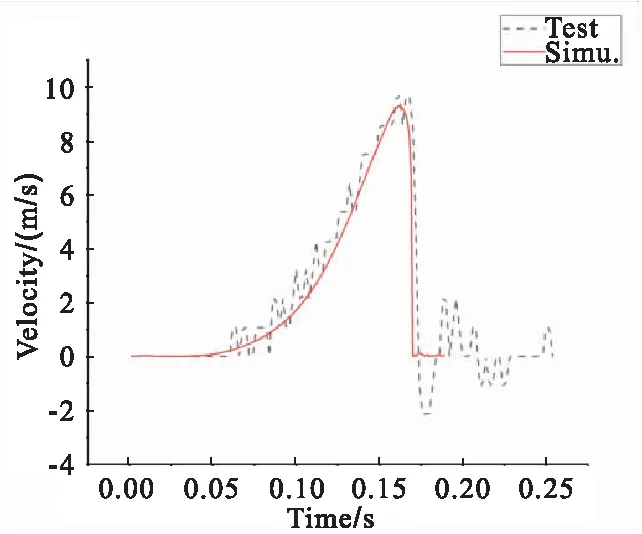
图5 展开速度仿真与实测对比Fig.5 Comparison between simulation and test results of velocity

3 Simulink联合仿真平台

由于在Ansys中无法对燃气发生器内部的燃烧过程进行模拟，而Matlab可以采用数值求解的方式，通过建立燃烧与膨胀做功的热力学模型，对燃烧过程进行计算。利用Ansys中的CoLink模块建立与Simulink之间的联系，将多体动力学的求解作为模块嵌入Simulink中，建立燃烧-展开的联合仿真模型。

3.1 微分方程组的建立

根据上文所述质量守恒方程、能量守恒方程，得可求解的偏微分方程组：

(13)

式(13)中，燃面Ab、作动筒位移szdt可直接求出；作动筒内温度Tzdt、作动筒内压强pzdt须通过方程组解出；如果采用简化的延伸喷管模型，作动筒速度vzdt、作动筒加速度azdt也可以通过微分方程解出；如果采用联合仿真，则可以考虑更详细的动力学模型，通过多体动力学求解器得出vzdt、azdt。

3.2 联合仿真平台的建立

将求解偏微分方程组的.m文件写成函数形式。由于Ansys求解模块无法嵌入偏微分方程求解中，故采用时间离散的方法逐步求解，框图如图6所示。联合仿真模型如图7所示。模型中，B为燃烧的肉厚，AAB为实际燃面面积，rm为单药片计算燃面面积，m为已燃烧药柱质量，其余变量与前文意义相同；main为微分方程求解主程序，rm/m为药柱燃烧参数求解程序，Ansys Client Block为多体动力学求解器，Memory1～9为对应参数初始值；由于现有装药形式为多片装药，Constant2表示装药片数；Switch为判断程序，当装药烧完后,燃面面积设置为Constant1；scope为监视器。

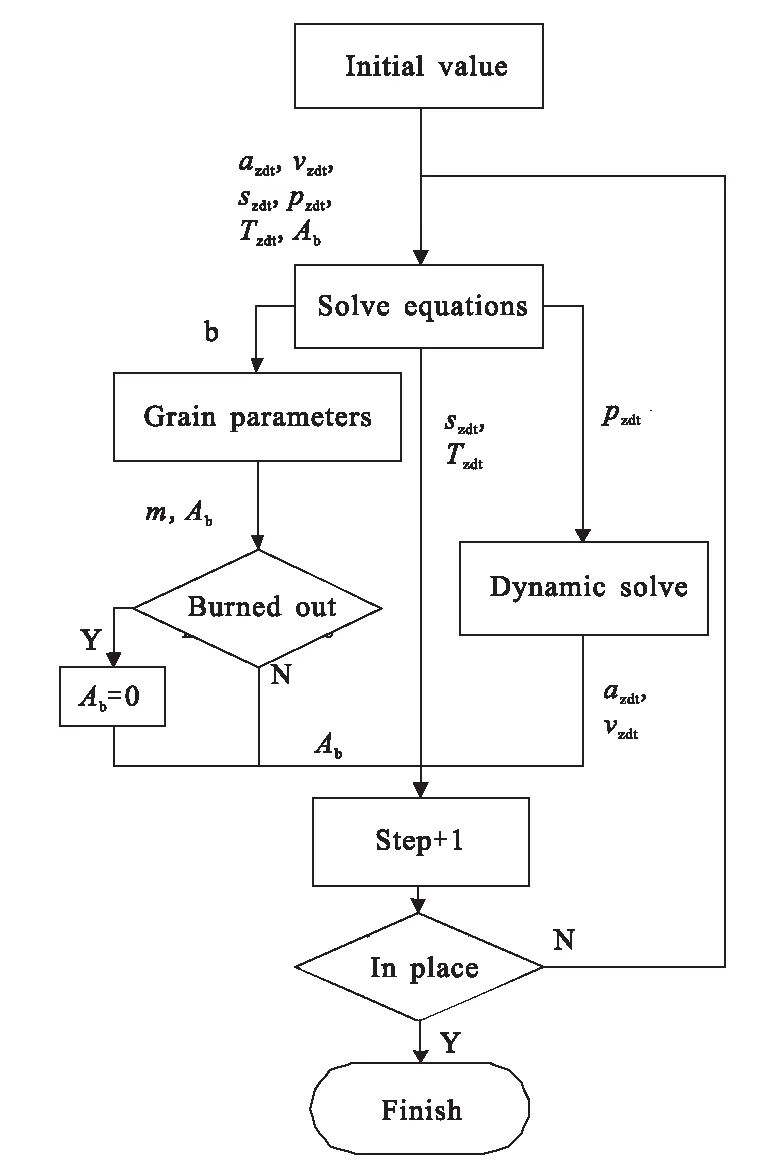
图6 联合仿真求解框图Fig.6 Co-simulation flow

图7 联合仿真模型Fig.7 Co-simulation model

由于是离散求解，无需考虑连续性问题，且为了避免求解中发生代数环(algebraic loop)错误，在每个循环中都加入Memory块。

4 仿真结果与分析

仿真中微分方程求解为龙格-库塔法，error tolerance设置为1e-7；整体仿真设置为discrete，步长为0.001，进行联合求解。

4.1 试验与仿真结果对比

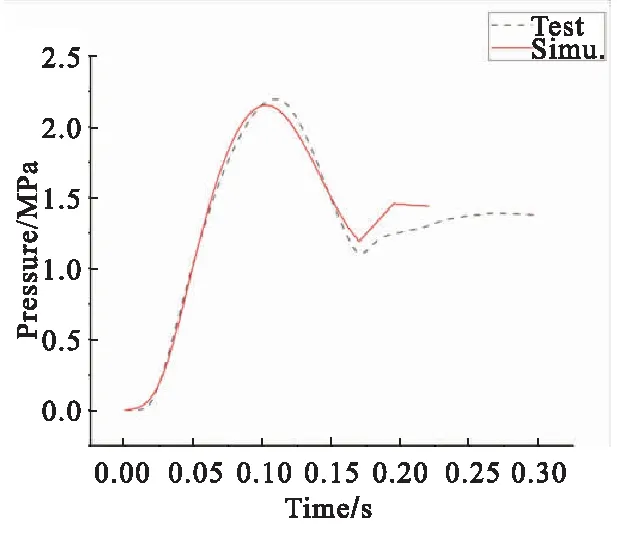
装药片数为7、4时，仿真获得作动筒内压力曲线与实测压力曲线对比如图8所示。作动筒展开速度曲线与实测速度曲线(高速录像获得)对比如图9所示。

(a)7 charge pellets

(a)7 charge pellets

如表1所示，由实测与仿真结果对比可以看出，不同药量下作动筒内压曲线与延伸锥展开曲线吻合程度较好，联合仿真模型可以较好的模拟出延伸喷管实际的点火-展开过程。

表1 药片数分别为7和4时仿真值与实测值对比

由数据对比可见，加入已燃烧药量的判定可以较为准确地预测出作动筒内压强的峰值、展开到位时压强值以及燃烧完毕时作动筒残压值，最大误差约10%。

4.2 仿真结果预测与分析

在不同药量下的延伸锥展开预测中，关键点在于作动筒内压曲线的获得。不同药量下作动筒内压数据如图10所示(8 pcs为预测数据)。可以看出，随着药量的上升，压强峰值、到位压强与残压均有提升，仅到位压强可以近似为比例关系；同时，作动筒到位时间、达到最大工作压强的时间、药柱燃烧时间均有缩短，但到位后燃气发生器继续工作的时间(药柱燃烧时间-作动筒到位时间)并不会随之缩短。所以即使在相同的外部边界条件下，不同药量的燃气发生器曲线变化规律也并非简单的线性关系。

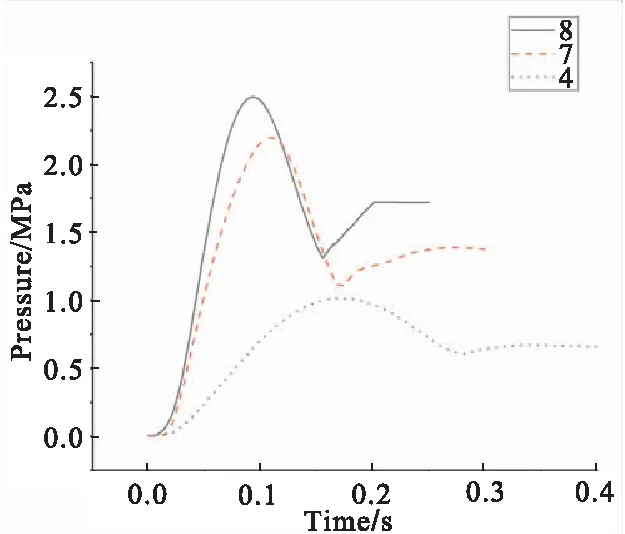
图10 不同药量下作动筒内压Fig.10 Pressure in the actuator under different charge pellets

在保持燃气发生器药量的情况下，若外部条件发生变化，如燃气尾流阻力变化等，延伸锥的展开曲线会受到较大影响，展开的最大速度也会发生变化；同时，作动筒内压曲线也会相应变化。由仿真分析可以得出，不同展开阻力下延伸喷管的展开情况如图11、图12所示。

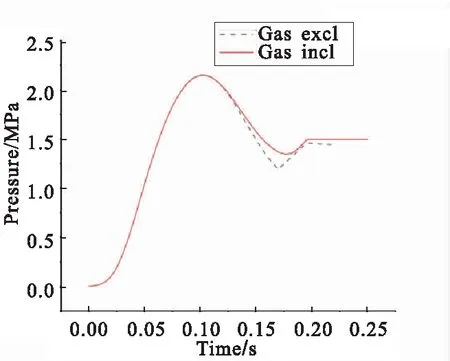
图11 不同阻力下作动筒内压Fig.11 Pressure in the actuator under different resistance

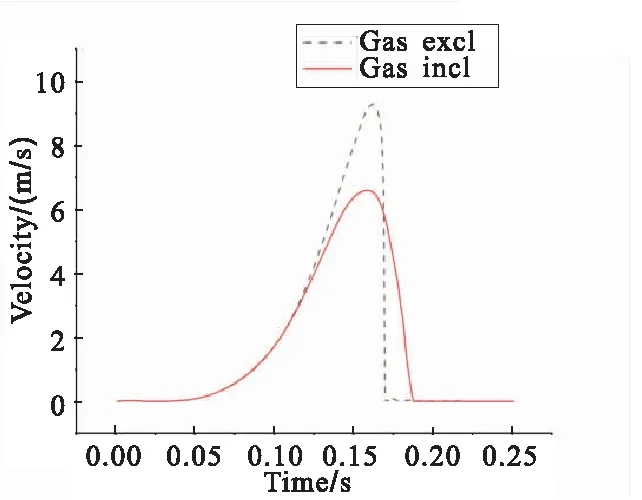
图12 不同阻力下延伸锥展开速度Fig.12 Extending velocity of the exit cone under different resistance

可以看出，在燃气尾流的影响下，展开速度明显下降；同时作动筒内压升高，到位时间增加，展开到位时作动筒压强也有所升高。因此，在外部边界条件改变的时候，作动筒内压曲线也会相应产生变化。又由于燃气发生器内压与作动筒内压相关，故燃气发生器内的燃烧情况也会随外部边界条件的变化而改变。

5 问题与讨论

模型中较为模糊的点在于燃烧室压强pc与作动筒压强pzdt的关系。如前文所述，作动筒内压pzdt(因变量)应为燃气发生器内压pc、时间t(自变量)的单值函数，即：

pzdt=f(pc,t)

(14)

但由于试验条件原因，无法准确测得燃气发生器内压pc的值，只能获得作动筒内压pzdt。为反应出pzdt对pc的影响，在仿真中采用近似的关系式：

pc=k1pzdte-k2pzdt

(15)

二者随时间变化的压强曲线对比如图13所示。

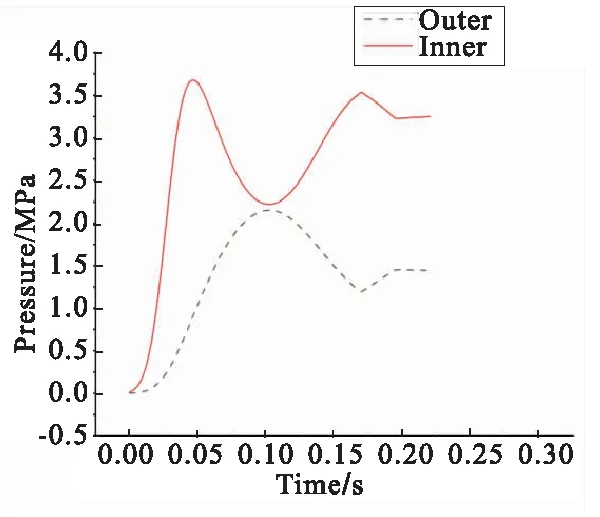
图13 燃气发生器内外压强对比Fig.13 Comparision between the pressure in the gas generator (inner pressure) and the actuator (outer pressure)

由于最终的仿真曲线重合度较高，可以近似认为燃气发生器内压曲线与实际状况一致。可以看出，在燃气发生器点燃的初期，作动筒内压较小，燃气发生器内压快速上升；随着作动筒内压逐渐上升，作动筒展开加速度变快，同时燃气发生器内压下降；在展开即将到位时，作动筒内压下降，燃气发生器内压再次上升，在药柱燃烧完毕后停止。

最终单位时间药柱燃烧质量曲线如图14所示。可以看出，不同药量下质量流率变化趋势基本一致。在展开初期，质量流率快速上升，在作动筒展开时先降后升，在展开到位后缓慢下降。另外，随着药量的下降，燃面面积与燃速均有下降，质量流率降低，燃烧时间上升。

图14 不同药量下燃气发生器质量流率曲线Fig.14 Mass flow rate under differentcharge pellets

为进一步完善仿真模型，后续需要对燃气发生器内压曲线进行准确的测量，以期获得燃气发生器内压、作动筒内压(燃气发生器外压)与时间三者的函数关系，或者通过流场计算得出 ，才能对延伸喷管点火-展开全过程进行更加准确的模拟。

6 结论

本文通过分析延伸喷管燃烧-传递-做功-展开的全过程，建立了燃气发生器装药点火燃烧与燃气做功的数学模型，以及延伸喷管展开的动力学模型，并采用联合仿真平台将进行耦合仿真。结论如下：

(1)联合仿真计算结果与试验数据一致性较好，表明联合仿真模型合理，仿真计算方法正确，仿真计算结果可靠；

(2)随着燃气发生器药量的提高，作动筒内压峰值提高，到位时间提前且残压上升；

(3)若延伸喷管外部阻力上升，作动筒内压会相应提高，但展开最大速度下降，到位时间增加；

(4)仿真模型可以较好地预估出在不同燃气发生器药量、不同发动机工作条件下的延伸喷管展开位移曲线，为在不同工况下的药量调节提供的可靠的参考，具有较强的工程应用价值；

(5)仿真计算中发现，燃气发生器内压、作动筒内压、燃气发生器工作时间三者间存在较强的关系，研究其变化规律有助于进一步完善仿真模型，以获得更准确，适用范围更广的结果。