概率论教学中如何分散难点

张艳伟 秦孝艳

摘要：在概率论的教学中能否恰当合理地运用“分散难点”的教学方法，是反映教师教学水平的一项重要指标，也是教好概率论的一种保障。文章通过在概率概念、概率计算、概率理论与概率教学结构的建构四个方面的教学中，论述如何运用“分散难点”的教学方法，展现了“分散难点”的教学方法在概率论教学与学习中的重要作用。

关键词：概率论;教学;分散难点

中图分类号：G642.4     文献标志码：A     文章编号：1674-9324（2020）15-0286-03

教学中能否恰当合理地运用“分散难点”的教学方法，是教师教好学的一种重要的教学方法与手段。因为再难的问题只要把难点分散就会变得容易，反之，再容易的问题把难点集中到一块也将变成难的问题。因此在教学中要求教师小到一堂课、一个定理、一个概念，大到整个学科，都应恰当、合理的运用好“分散难点”的教学方法，从而获得更好的教学效果。

概率统计作为现代数学的重要分支，在自然科学、社会科学和工程技术的各个领域都具有极为广泛的应用。正是概率统计的这种广泛应用性，使得它成为各类专业大学生的重要的数学必修课之一。不同于确定数学，概率论是研究随机现象及其统计规律的数学学科。故在数学教学中，概率论是教师比较难教、学生比较难学的一门数学课程，所以在概率论的教学中能否恰当、合理的运用“分散难点”的教学方法，就显得更为重要。下面从四个方面简述在概率论教学中如何运用“分散难点”的教学方法。

一、“概率概念”教学中如何分散难点

在概率概念教学中分散难点，就是通过概率概念的产生、发展过程中所体现的数学思想方法以及数学概念的教学要求[掌握概念的内涵（定义），明确概念的外延（分类）]进行分散，构造教学结构，实施教学。

定义1（概率）：设F是一事件域，在F上定义实值集函数P，对每一事件A∈F，函数值为P（A），如果它满足如下三个条件：

定义中所体现的数学思想方法：①P（A）是事件A的单值实函数。②P（A）满足非负性、规范性、可列可加性。③P（A）的定义域是事件域F。

在概率概念教学中，按以下三个顺序分散讲授：

1.描述定义。在概率论中事件的发生都是随机的，但却存在着统计规律，即每个事件发生的可能性的大小是客观存在的、确定的。这样我们就可以依据每个事件发生可能性的大小来研究随机现象。我们把表示事件发生可能性大小的数，即事件A的单值实函数，称为事件的概率（概率的描述定义）。

2.概率的性质。概率的描述定义虽阐明了概率的本质含义，但却无法知道事件概率的确定值。为了求出概率的确定值，人们根据对随机现象长期探究的实践，总结出概率的统计定义与古典定义。在这两个定义中，概率都具有非负性、规范性、有限可加性三条基本性质。

3.事件域。样本空间Ω的子集（事件），不一定都是可测的，有时存在不可测的子集，即概率不存在的子集（事件），而概率论只需研究概率存在的事件，这样我們就把概率存在的事件组成的集合称为事件域。

综上所述“事件概率”概念的教学结构为：描述定义→统计定义→古典定义→事件→概率定义（数学定义）。

二、“概率计算”教学中如何分散难点

在概率计算教学中分散难点，就是通过概率计算的方法中所体现的数学思想方法，进行分散，构造教学结构，实施教学。

古典概率计算中，一种重要求概率的方法就是利用排列组合求概率，它也是概率教学中的一个难点。在教学中对它我们可以这样分散难点：复习归纳排列组合有关知识→学习在概率论中应用的主要类型→学习利用排列组合求概率的有关问题与方法，其教学结构如下：

1.排列组合有关知识。理论：加法原理与乘法原理。

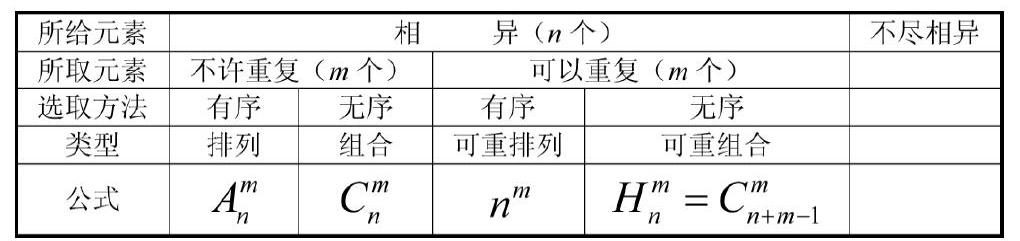
类型：

2.在概率论中应用排列组合的主要类型。

（1）抽球（样）问题：从n个不同的球中，一次抽一个球。

①无放回地抽m个球，排成一排，有多少不同结果（排列问题）。

②无放回地抽m个球，组成一组，有多少不同结果（组合问题）。

③有放回地抽m个球，排成一排，有多少不同结果（可重排列问题）。

④有放回地抽m个球，组成一组，有多少不同结果（可重组合问题）。

（2）分房（占位）问题：m个人分到n个房间去住（m

①房间认为是不同的，每个房间只住一个人，有多少不同结果（排列问题）。

②房间认为是相同的，每个房间只住一个人，有多少不同结果（组合问题）。

③房间认为是不同的，每个房间住的人数不限，有多少不同结果（可重排列问题）。

④房间认为是相同的，每个房间住的人数不限，有多少不同结果（可重组合问题）。

（3）利用排列组合求概率的基本思想方法。

①合理构建样本空间，决定是用排列思想还是用组合思想求概率。若是既能用排列思想也能用组合思想求概率，通常用排列思想求概率，因为用组合思想求概率很容易出错。

②复杂问题：分步计算，先选后排。

4.利用排列组合求概率的常见问题。

①概率论中的排列问题：相邻问题、分隔问题、循环问题、对称问题、可重排列问题、不尽相异元素排列问题…等。

②概率论中的组合问题：搭配问题、分班问题、分堆问题、可重组合问题等。

三、“概率理论”教学中如何分散难点

概率论中的重要理论是大数定律和中心极限定理。在概率理论教学中分散难点，就是通过概率理论的产生、建立、完善过程中所体现的数学思想方法与实例，进行分散，构造教学结构，实施教学。

在中心极限定理的教学中，我们可以通过中心极限定理的产生过程中所体现的数学思想方法，分散难点，进行教学，以加深学生对中心极限定理的理解与掌握。

人们在实践中发现，许多随机现象都服从正态分布，于是提出两个问题：（1）为什么正态分布广泛存在。（2）满足什么条件的随机现象服从正态分布。这两个问题从18世纪开始，在长达两个世纪的时间内成为概率论研究的中心，对这两个问题研究得出的有关理论称为中心极限定理。

通过对这两个问题的研究得出：如果某个随机变量，是由许多独立随机变量的总和组成，而每个随机变量对于总和都不起主要作用，那么这个随机变量就近似地服从正态分布。

因现实世界中，许多随机现象都是由一些独立随机现象的总和组成，且每个随机现象对于总和都不起主要作用，故服从正态分布的随机现象较多。在独立同分布的中心极限定理中，每个随机变量都是独立同分布，故不存在起主要作用的随机变量，所以和式近似服从正态分布。

四、“概率教学结构的建构”教学中如何分散难点

在概率教学结构的建构教学中分散难点，一种方法就是在已知教学结构构建过程中，所体现的数学思想方法的基础上，通过类比推广增加建构新的教学结构，进行分散，实施教学。

对于二维随机变量分布的教学结构的建构，就是依据一维随机变量分布的教学结构，通过类比推广增加的方法，进行分散，从而建构出二维随机变量分布的教学结构。

1.一维随机变量分布的教学结构：

（1）离散型。

①定义，②表示法，③性质，④常见分布，⑤函数分布。

（2）连续型。

①定义，②分布密度性质，③常见分布，④函数分布。

2.依据一维随机变量分布的教学结构，通过类比推广增加，建构二维随机变量分布的教学结构：

通过类比与一维随机变量分布教学结构类似的内容：

（1）离散型。

①定义，②表示法，③性质，④常见分布，⑤函数分布。

（2）連续型。

①定义，②分布密度性质，③常见分布，④函数分布。

因二维随机变量含有二个变量，故需要推广增加有关它们间关系的内容。在二维随机变量分布的教学结构中需要推广增加的内容：

（1）离散型。

⑥边际分布，⑦独立性，⑧条件分布。

（2）连续型。

⑤边际分布，⑥独立，⑦条件分布，⑧极值的分布。

总之，在概率论教学中恰当合理地运用“分散难点”的教学方法，就能实现教师轻松讲、学生轻松学，就能使教学成为艺术享受，就能使学生学得更好，同时它也是反映教师教学水平的一项重要指标。

最后还应该指出的是，“分散难点”没有固定、明确的一般方法，要具体问题，具体分析，但只要教师在备课与教学过程中，始终想到如何提高教学质量，如何使学生学得更好，那么在教学中就一定会体现“分散难点”的教学思想或创建出“分散难点”一些具体方法。

参考文献：

[1]宋长明，张建林，江世景.案例教学法在概率统计教学中的应用[J].开封教育学院学报，2009，29（4）：76-77.

[2]陈建兰，胡晓敏.概率论与数理统计课程教学改革的研究与探讨[J].教育教学论坛.2014，（20）：49-50.

[3]茆诗松，程依明，濮晓龙.概率论与数理统计[M].北京：高等教育出版社，2011.

[4]盛骤，谢式千，潘承毅.概率论与数理统计[M].北京：高等教育出版社，2008.

[5]缪铨生.概率与统计[M].上海：华东师范大学出版社，2007.

[6]牛家骥.认识数学[M].吉林：吉林大学出版社，2017.