卫星光通信精确跟踪控制系统的参数化综合优化设计

段广仁,王建宇,赵天一,张 亮

(1.哈尔滨工业大学控制理论与制导技术中心,黑龙江 哈尔滨 150080;2.中国科学院上海技术物理研究所空间主动光电技术重点实验室,上海 200083)

1 引言

量子通信是量子物理与信息科学的新型交叉学科,在保密安全性上具有经典通信无法比拟的优势,是近年来国际研究的热点课题.基于卫星的量子通信摆脱了光纤的距离束缚,为全球量子通信网的建立提供了有效途径.

量子通信链路的实现依赖于高精度捕获跟踪瞄准(acquisition,tracking and pointing,ATP)系统.由于空间尺度量子通信系统中量子光发散角仅10µrad左右,因此动态情况下通信链路的建立和维持是系统的重点和难点.

由于国内激光通信研究开展较晚,导致国内的ATP技术发展较为有限.国外ATP技术的研究与发展已历经近30年,发展已较为成熟,并已经多次成功地应用在星间及星地通信试验当中[1].目前国际上关于ATP技术比较有代表性的项目有欧空局的SILEX计 划[2–3]、Space-QUEST 计 划[4],日 本 的ETS–VI计划[5]、OICETS计划[6–7]等等.SILEX计划的终端采用了大范围精指向机构,粗指向机构可以以开环状态工作[2–3].ETS–VI计划的LCE终端采用小范围二维指向镜作为粗指向机构,与探测器闭环跟踪精度高,因此精跟踪机构的波动范围较小[5].OICETS 计划的LUCE终端采用二维转台作为粗指向机构,优势是跟踪范围较大,不足是跟踪的精度稍低;精跟踪机构与ETS–VI计划、SILEX计划的相比跟踪范围较大[6–7].

目前国内外的ATP系统大多采用了精、粗对准系统分别设计的方式,子系统内部则采用了传统的PID控制架构.欧洲宇航局(ESA)主导的SILEX计划的ATP系统包含了粗跟踪系统、精跟踪系统和超前瞄准系统3个子系统.各个子控制系统分别独立采用了古典PID控制方式[2–3].日本主导的ETS–VI计划[5]和OICETS计划[6–7]的ATP系统同样采取了这种粗跟踪系统、精跟踪系统和超前瞄准系统的控制系统架构.其中,OICETS计划将精跟踪环嵌套于粗跟踪环当中,而将超前瞄准子系统独立开来.粗跟踪子系统包含电机驱动的转台结构,具有较大的粗跟踪范围.2008年美国航空航天局(NASA)开启了月地激光通信演示验证(LLCD)计划,将激光通信研究推入了深空阶段.相比于近地激光通信,深空超长链路的环境更为复杂和恶劣,空间终端只能依靠极弱的光信号进行高带宽的跟踪以维持通信链路稳定.为此,LLCD计划基于精、粗跟踪系统分别设计的思想,采用了主被动相结合的跟踪控制方案.这种基于本地稳定平台的主被动结合的控制策略不仅解决了极弱光强的跟踪问题,同时还减缓了光学跟踪频率从而弱化了空间终端对大气干扰的敏感性[8–9].

国外的ATP跟踪精度已经达到了较高的水平.在量子科学实验卫星中载荷对地的快速捕获,初始捕获时间平均1.1 s,丢失后重捕获0.3 s,载荷跟踪精度最优达到0.5µrad(1σ),系统指向误差小于1µrad;实现了一星对双站的高精度光链路跟踪;文献[11]摘录了日本、欧洲最具代表性的激光通信中的跟踪指向性能测试情况.日本OICETS项目中跟踪精度小于0.2µrad(1σ),系统指向误差修正前3µrad,修正后小于1µrad(见文献[11]第2–3页);欧洲SiLEX计划中,终端捕获时间平均68 s,跟踪精度小于0.2µrad(1σ),系统指向误差0.85～1.5µrad,(见文献[11]第5–6页).(以上误差分为了两项,一项是跟踪精度,也就是与控制跟踪有关的误差;另一项是系统指向误差,指的是发射光轴与接收光轴之间的系统偏差,一般与自动控制无关,而与结构、热稳定性有关.这次本文只涉及前一项误差.)

在中国科学院空间科学战略性先导专项项目支持下,我国成功发射了墨子号量子科学实验卫星,完成了多项星地量子科学实验任务,在空间尺度量子通信方面取得重大进展.从工程技术的角度,基于经典随动系统理论方法,完成了高精度捕获跟踪与瞄准系统的设计实现,在轨实测跟踪精度优于0.5µrad(1σ),满足空间量子通信链路需求[10].

前期项目中精准对准系统采用了经典的PID控制方式,取得了良好的控制效果.未来空间量子通信将向更高轨道更远距离发展,其对控制的精度提出了更高的要求,已有的传统的控制方法难以满足.因此,本文针对该项目第二期的预先研究,开发了一种新的精确对准系统的参数化设计方法.不同于传统的控制方法,参数化方法通过首先建立控制律的完全参数化表示,然后综合优化控制律中的自由参数来实现控制系统的多目标设计要求,如闭环极点对参数摄动不灵敏设计[12–13]、干扰抑制设计[14–15]、增益调度设计[16–17]等,因而相较于其他设计方法更加灵活、方便,具有更加广泛的适用范围.本文设计的控制律同时考虑了精度、阶跃干扰解耦、干扰抑制、对参数摄动不敏感等方面.从仿真结果上看,本文设计的参数化方法的控制效果在对准精度、干扰抑制能力等方面要远远优于传统的控制方法,对准精度由原来的微弧度量级提高到了纳弧度量级.

2 问题描述

2.1 控制系统构成

在项目中,粗跟踪机构(可使用二维转台或二维指向镜)与粗跟踪探测器构成粗跟踪光闭环系统,实现对地面站信标光的捕获及粗跟踪,将光束引入望远镜及后光路.精跟踪机构即压电陶瓷快速反射镜与精跟踪相机构成精跟踪光闭环系统,对粗跟踪的残差进一步抑制,量子发射及接收则通过分光合束器件与跟踪单元共光路(见图1).具体控制系统结构如图2所示.

2.2 状态空间模型

系统的开环模型如图3所示.

选取如下状态向量:

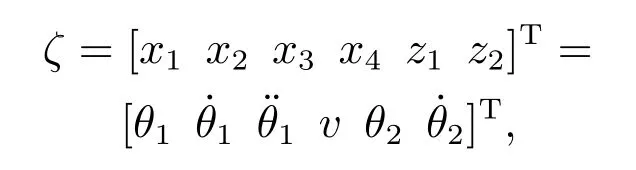
并将控制向量定义为u=[u1u2]T.

引入如下记号:

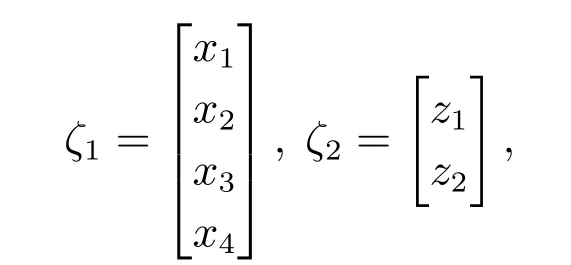
则根据框图3,容易导出开环系统的状态方程如下:

其中:d是外部干扰,

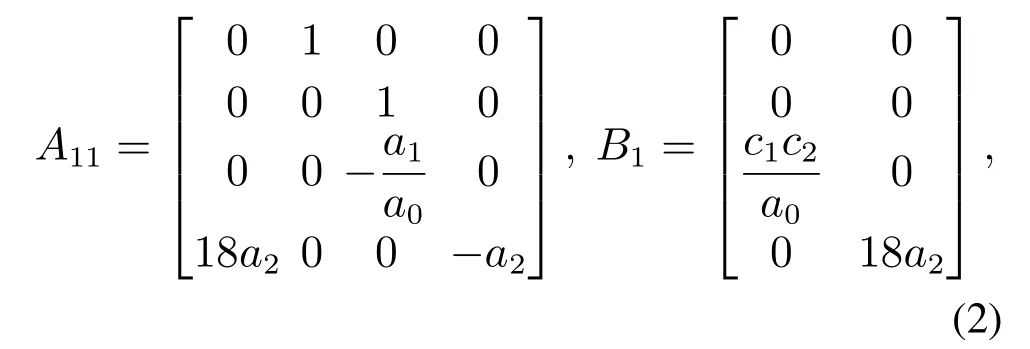
根据物理背景可知系统的量测输出方程为

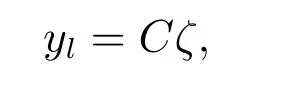
其中C=[I50].

图1 精确对准系统物理结构图Fig.1 Physical structure diagram of precise alignment system

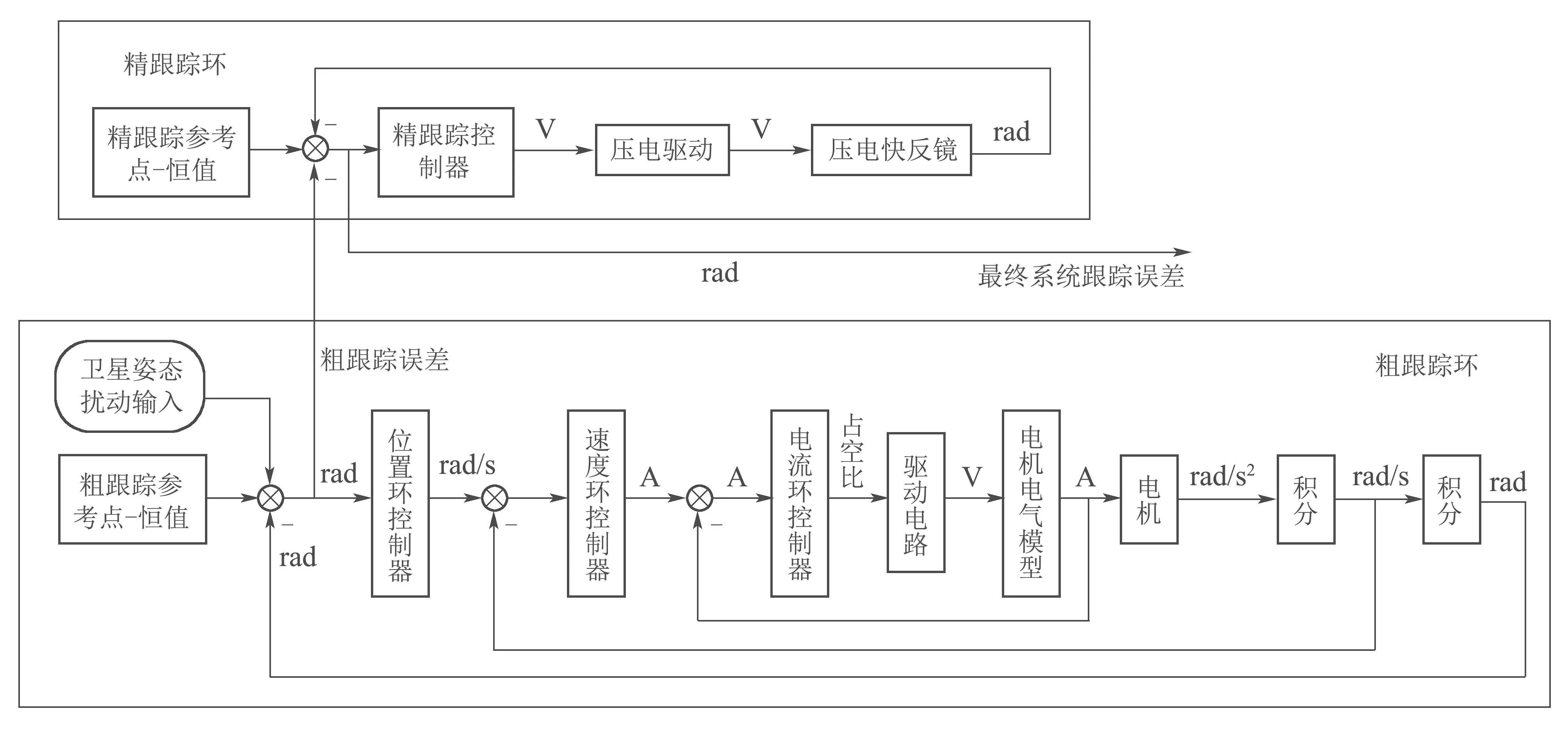
图2 基于经典方法的控制系统Fig.2 Control system based on classical method

图3 开环系统框图Fig.3 Open loop system block diagram

2.3 问题的描述

根据实际任务需求,希望对准系统的角度输出θ1和θ2渐进跟踪给定的定常参考信号,因此引入如下的受控输出方程:

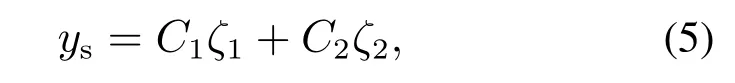
其中:

本文想要解决的问题可以描述如下:

问题1给定系统(1),设计线性反馈控制律,使得如下条件被同时满足:

1)闭环系统的受控输出ys渐近跟踪给定的定常参考信号yr;

2)闭环系统的受控输出ys对阶跃的干扰信号完全解耦;

3)闭环系统是非退化的,且具有期望的复共轭闭环极点;

4)闭环系统具有较小的特征值灵敏度;

5)闭环系统由干扰d到最终角度输出θ2的传递函数Gdθ2(s)具有尽可能小的H2范数;

6)反馈增益矩阵具有尽可能小的范数.

3 准备工作

3.1 渐近跟踪

考虑下述线性定常系统:

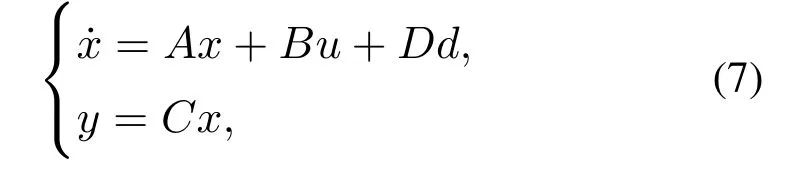
其中:x ∈Rn,u ∈Rr,y ∈Rm和d ∈Rl分别是系统的状态向量、控制输入向量、输出向量和干扰向量;A,B,D和C是适当维数的已知参数矩阵.

在许多实际问题中,希望设计控制律u,使得控制系统的输出y(t)能够渐进跟踪某一给定的定常参考信号yr,即.

引入如下新的变量q(t)

则有

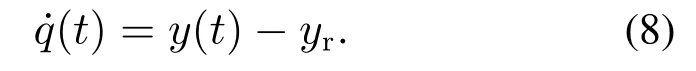
联立式(7)–(8),可得如下增广系统:

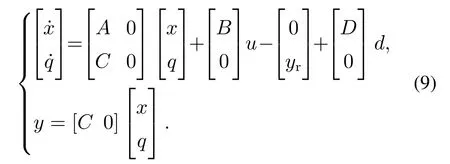
针对该增广系统设计如下状态反馈控制律:

显然,控制律(10)相对于系统(7)是一个广义的PI控制器.

引理1[18]如果式(10)是增广系统(9)的一个状态反馈镇定律,则在干扰d为定常的条件下,系统(7)可以在控制律(10)的作用下实现其输出对于阶跃信号yr的渐近跟踪,同时对干扰d完全解耦.

3.2 状态反馈参数化设计

针对系统(7),设计如下状态反馈控制律:

希望在控制律(11)的作用下,闭环系统是非退化的,并拥有期望的复共轭极点si,i=1,2,···,n.

根据文献[19]的理论,依次对矩阵[siI −A−B],i=1,2,···,n进行奇异值分解,进而得到正交矩阵Pi,Qi,i=1,2,···,n,使得

若对矩阵Qi,i=1,2,···,n,进行如下分块:

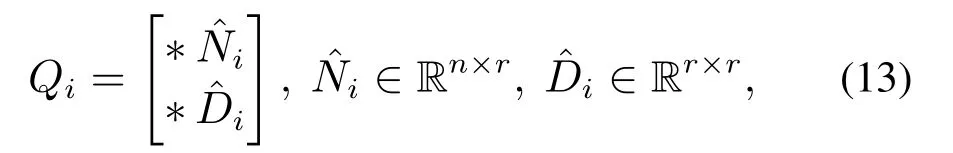
则根据式(12),有

有了以上准备,根据文献[19]的理论,有以下结论.

引理2设 系统(7)能控,设Rr×r,i=1,2,···,n为由式(12)–(13)给出的矩阵.则所有能使闭环系统非退化并拥有期望的复共轭极点si,i=1,2,···,n的控制律(11)可以由下式给出:

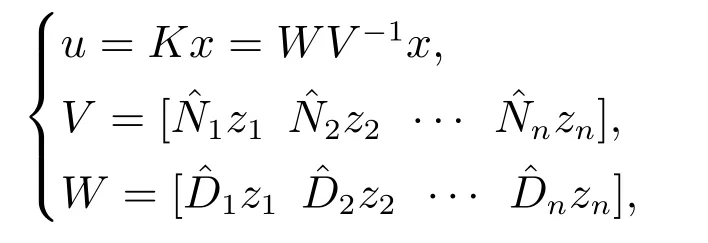
其中zi ∈Cr,i=1,2,···,n为满足如下约束的参数向量:

3.3 干扰抑制

线性定常系统(7)在状态反馈控制律(11)作用下的闭环系统为

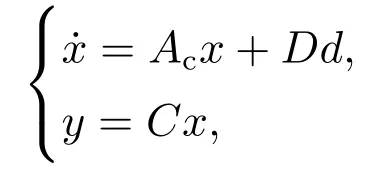
其中

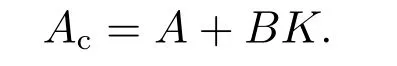
希望干扰d对输出y的影响尽可能小,为此可以极小化

的H2范数.

引理3[15]设Ac∈Rn×n,B ∈Rn×r,C ∈Rm×n.若矩阵Ac的特征值均具有非正实部,则

1)如下两个Lyapunov方程均存在唯一的对称半正定解P1和P2:

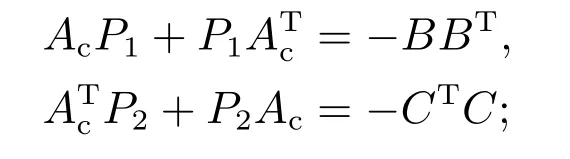
2)如下的关系式成立:

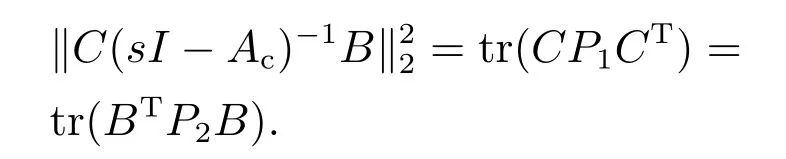
4 控制系统设计

4.1 控制器结构

引入如下记号:

其中:A11,A21,A22,B1由式(2)–(3)给出;C1,C2由式(6)给出.

定理1设yr∈R2是给定的定常参考信号,由式(14)给出,A,B由式(15)给出.设矩阵,(A+BK)的特征值均具有负实部,则系统(1)(5)在如下控制律的作用下:

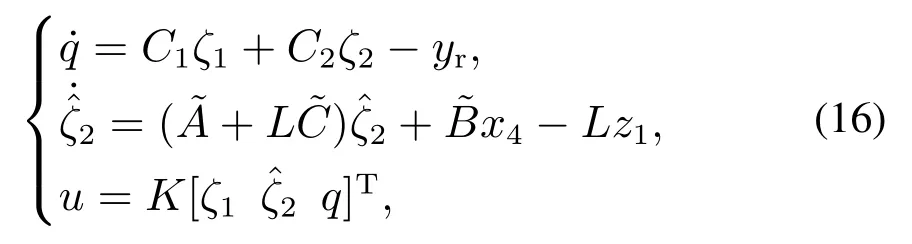
有如下结论:

1)闭环系统的受控输出ys渐近跟踪给定的定常参考信号yr;

2)闭环系统的受控输出ys对阶跃的干扰信号d完全解耦.

证容易看出ζ2子系统的状态空间模型为

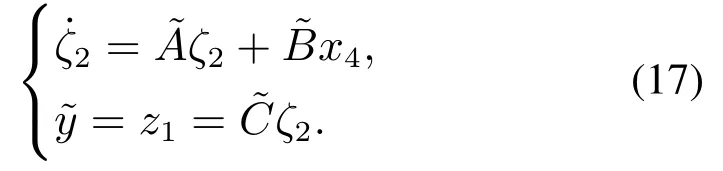
若引入变量

则式(16)的第2个表达式可以改写为

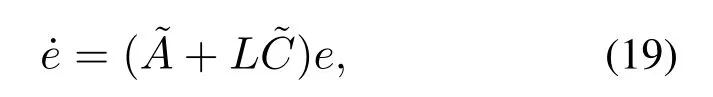
若将矩阵K进行如下分块:

同时考虑到式(18),则式(16)的第3个表达式可以改写为

综合开环系统(1)与控制律(16),并将表达式(19)–(20)代入,可得如下闭环系统:

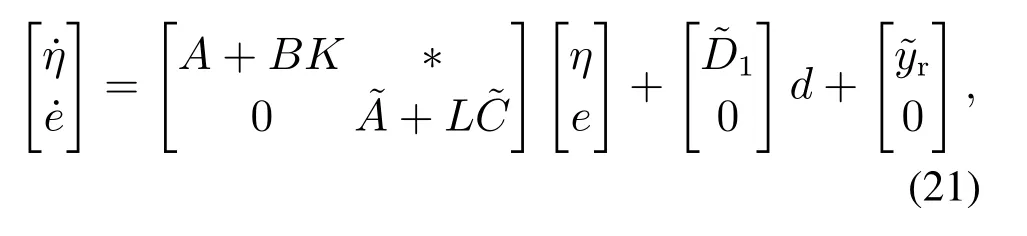
其中:

4.2 观测器设计

由定理1的证明不难看出,式(16)的第2个表达式本质是ζ2子系统的全维状态观测器.本节考虑该观测器的设计方法.

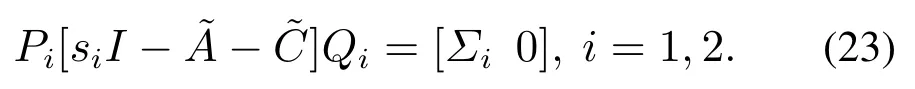
若对矩阵Qi,i=1,2,进行如下分块:

则有

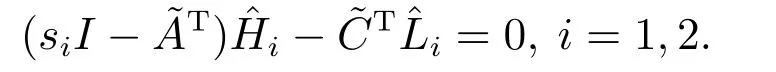
有了以上准备,根据第3.2节展示的结果,观测器的增益矩阵L可以由下式给出:

定理2给定系统(1).设由式(14)给出,A,B由式(15)给出.若稳定,则

1)(极点分离原理)在控制律(16)的作用下的闭环系统的极点集,是矩阵(A+BK)和的特征值集合的并;

2)(传递函数分离原理)在控制律(16)的作用下的闭环系统由干扰d到最终角度输出θ2的传递函数可以由下式给出:

其中:e5∈R8代表第5个元素是1,其余元素是0的向量,由式(22)给出;

3)(特征值灵敏度分离原理)在控制律(16)的作用下的闭环系统的特征值灵敏度由矩阵(A+BK)和的特征向量矩阵的条件数决定.

证与定理1的证明过程类似,将控制律(16)代入开环系统(1),并将表达式(19)–(20)代入,可得闭环系统(21).由式(21)容易看出

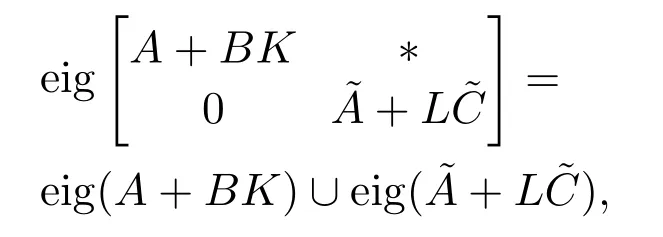
即定理的结论1成立.

考察闭环系统(21)由干扰d到最终角度输出θ2的传递函数

其中:

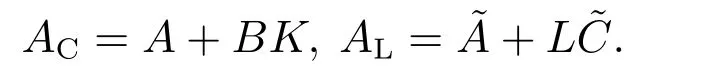
注意到分块矩阵的求逆引理,上式可以改写为

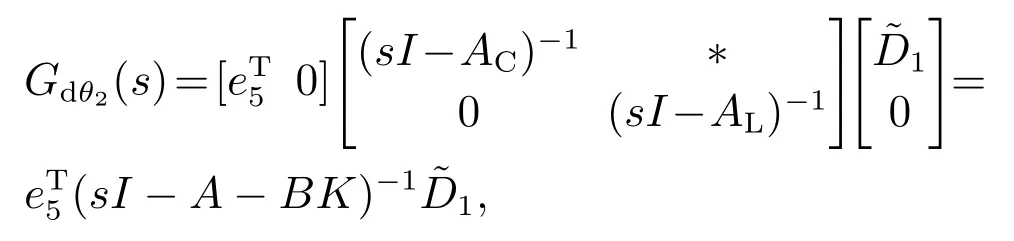
即定理的结论2成立.

由文献[9]可知矩阵(A+BK)和(˜A+L˜C)的特征值灵敏度分别取决于这两个矩阵的特征向量矩阵的条件数,又由定理的结论1可知闭环系统(21)的极点是矩阵(A+BK)和的特征值集合的并,因此显然定理的结论3成立. 证毕.

4.3 鲁棒反馈镇定律设计

本节考虑增益矩阵K的求取.

假设(A+BK)期望配置的极点为s1,s2,···,s8.利用第3.2节展示的理论,依次对矩阵[siI −A −B],i=1,2,···,8,进行奇异值分解,进而得到正交矩阵Pi,Qi,i=1,2,···,8,使得

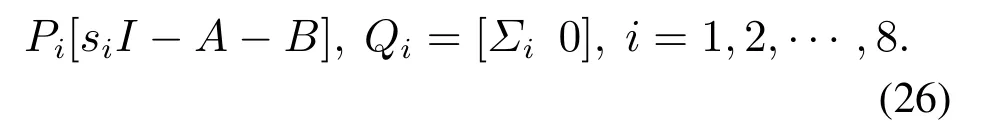
若对矩阵Qi,i=1,2,···,8进行如下分块:

则有

有了以上准备,根据第3.2节展示的结果,反馈增益矩阵K可以由下式给出:

其中fi ∈Cr,i=1,2,···,n为满足如下约束的参数向量:

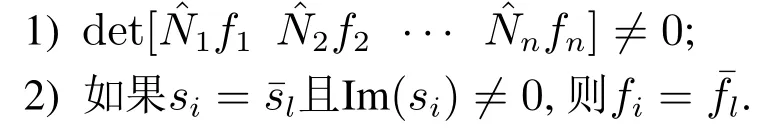
定理3给定系统(1).设A,B由式(15)给出.设s1,s2,···,s8为一组具有负实部的复共轭复数,K由式(28)给出.则

1)矩阵(A+BK)是非退化的且其特征值为s1,s2,···,s8;

2)若采用第4.2节展示的设计方法进行观测器设计,并取控制律(16),则闭环系统是非退化的,且其特征值为,s1,s2,···,s8;

3)由式(25)给出的传递函数Gdθ2(s)的H2范数可以由下式给出:

其中:

证根据第4.3节的设计方法以及第3.2节展示的结果,定理的结论1显然成立.由定理2可知在控制律(16)的作用下的闭环系统的极点集,是矩阵(A+BK)和的特征值集合的并,同时考虑到引理2,可知定理的结论2成立.

当K由式(28)给出时,有

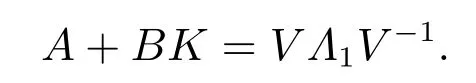
将上式代入到传递函数Gdθ2(s)的表达式(25)中,可得

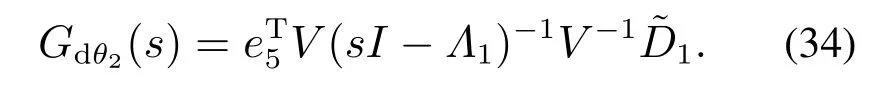
为了对上式应用引理3,考虑如下Lyapunov方程:

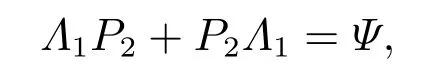
其中Ψ由式(32)给出.利用拉直运算,可得上述Lyapunov方程的解为式(30),则根据引理3,传递函数Gdθ2(s)的H2范数可以由式(29)给出.即定理的结论3成立. 证毕.

矩阵(A+BK)的特征向量矩阵的条件数可以由下式给出:

反馈增益矩阵K的范数可以由下式给出:

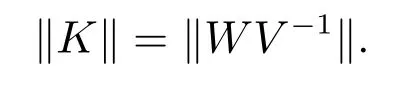
为了使闭环系统具有较小的特征值灵敏度以及尽可能小的反馈控制增益,同时使由干扰d到最终角度输出θ2的传递函数Gdθ2(s)具有尽可能小的H2范数,引入如下优化指标:

其中:αd,αc,αu≥0是权重系数,W,V由式(28)给出.求解如下优化问题:

注1可以看出式(35)是一个受约束的非线性优化问题,想要得到理论上的全局最优解比较困难.但可以事先确定待优化参数的大致范围,然后利用数值优化算法(如遗传算法、退火算法等)来求得问题(35)的局部数值最优解.

5 仿真分析

5.1 控制系统设计

开环系统(1)的参数值由表1给出.

表1 开环系统参数值Table 1 Open loop system parameter value

控制系统的Simulink 实现如图4 所示,矩阵(A+BK)期望配置的极点为

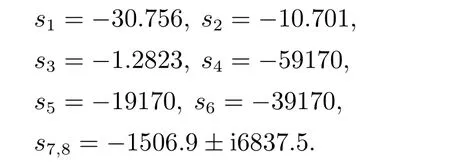
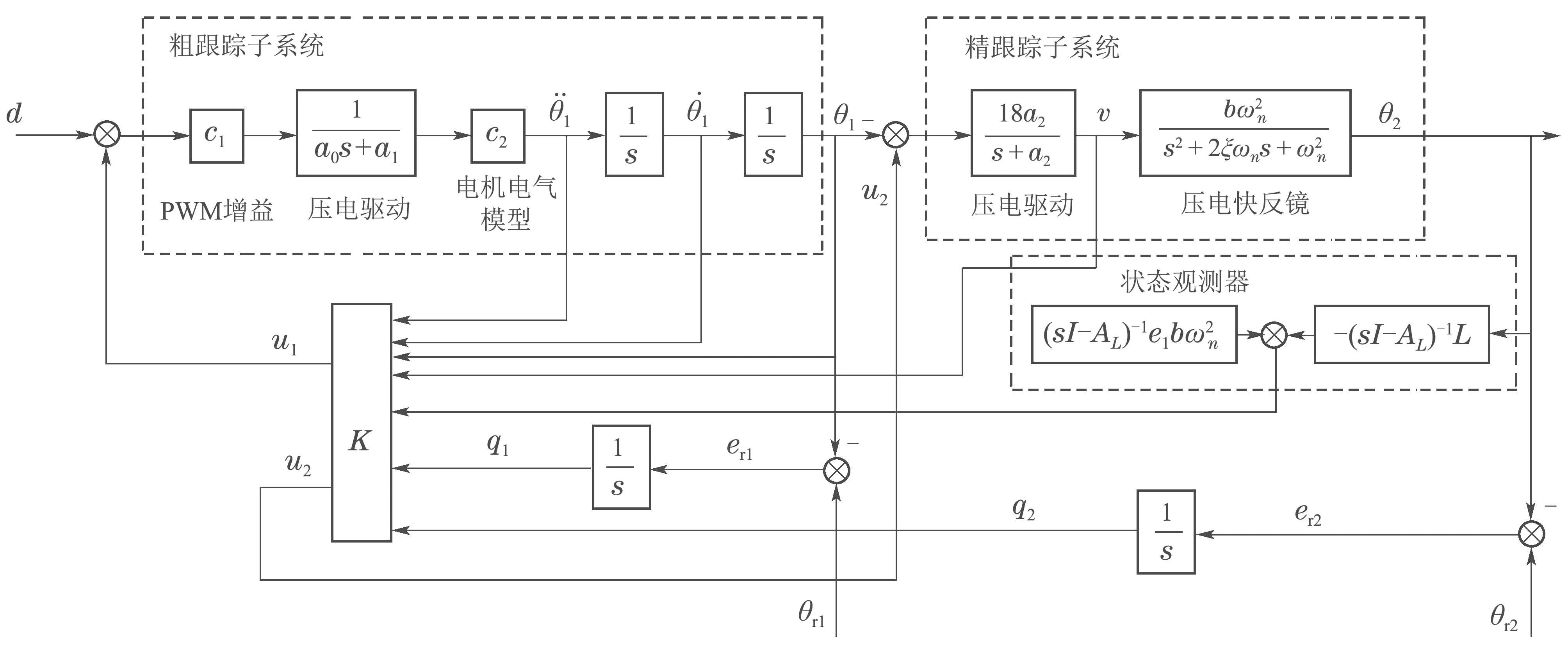
图4 参数化方法控制系统Simulink框图Fig.4 Simulink block diagram of the parametric method control system

求解优化问题(35),得到最优参数如下(仅展示5位有效数字):

将上述最优参数代入式(28),可得控制器的增益矩阵K为

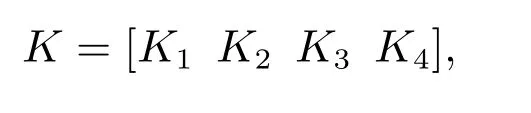
其中:

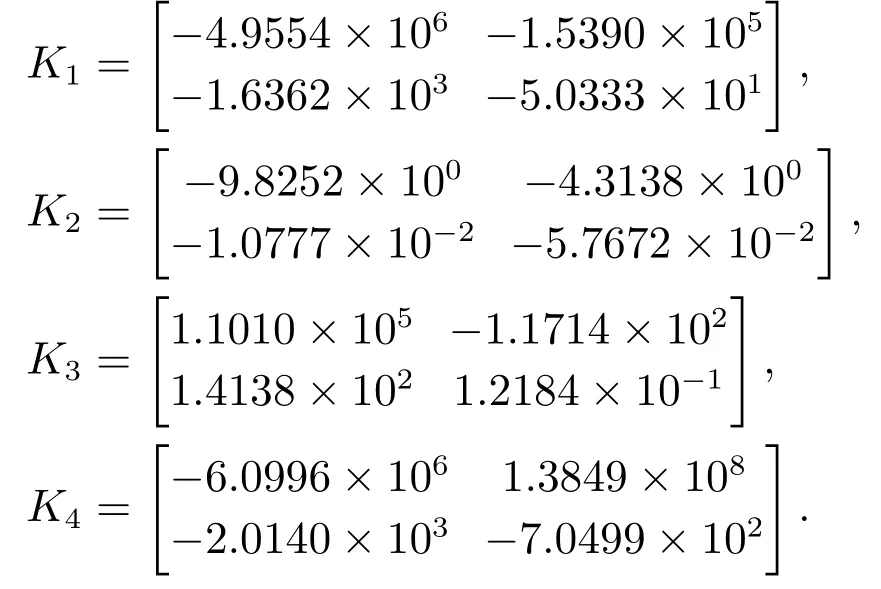
矩阵(A+LC)期望配置的极点为

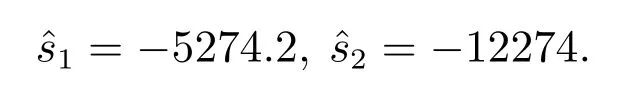
所设计的观测器的增益矩阵L为

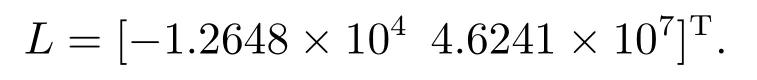
前期项目采用了经典PID控制方法,其控制系统Simulink实现如图5所示.

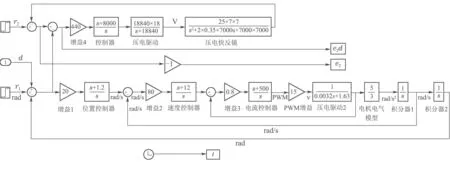
图5 经典方法控制系统Simulink框图Fig.5 Simulink block diagram of the classic method control system

5.2 大扰动情形

仿真环境与条件详述如下:

1)MATLAB与Simulink版本为2014a;

2)仿真算法采取Simulink软件中的ode23tb(stiff/TR–BDF2);

3)闭环系统的状态初值全部取为0.

将参考信号θr1选取为单位阶跃信号,参考信号θr2选取为0.为了测试控制系统的抗干扰能力与对准精度,考虑了大干扰的情形.将干扰信号d分别选取为如下3种情形:

情形1斜率为1的斜坡信号;

情形2幅值为1,角频率为0.5 rad/s,初相位为0的正弦信号,即

情形3方差为1×10−4的高斯白噪声(生成信号的步长为0.001 s).

引入最终角度跟踪误差e2=θr2−θ2,则在上述3种情形下e2的响应曲线如图6所示,对应的控制输入u1,u2的曲线如图7所示.

作为对比,还进行了经典控制方法的仿真.将参考信号θr1和θr2均设置为1,仿真环境与条件同上,并采取了相同的干扰信号.得到的e2的响应曲线如图8所示,控制输入u1,u2的曲线如图9所示.

注2参数化方法和经典方法选取了不同的参考输入数值,这是由于经典方法是基于与基座的相对坐标来进行的跟踪控制系统设计,而本文提出的参数化方法则考虑的是相对惯性坐标系的绝对角度跟踪.因此,虽然参考输入数值选取的不同,但本质上跟踪的角度是相同的.

图6 大扰动情形参数化方法对准精度Fig.6 Parameterization method alignment accuracy under large disturbance

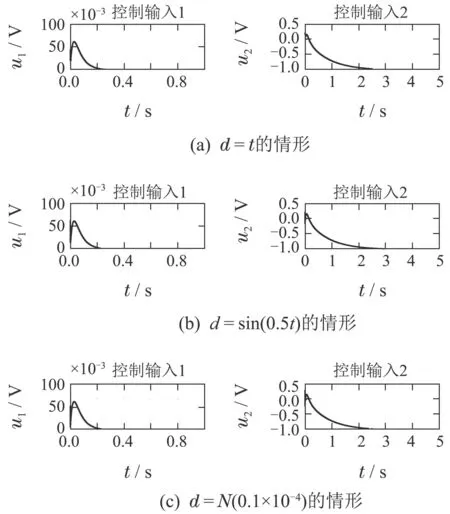
图7 大扰动情形参数化方法控制输入Fig.7 Parameterization method control inputs under large disturbance

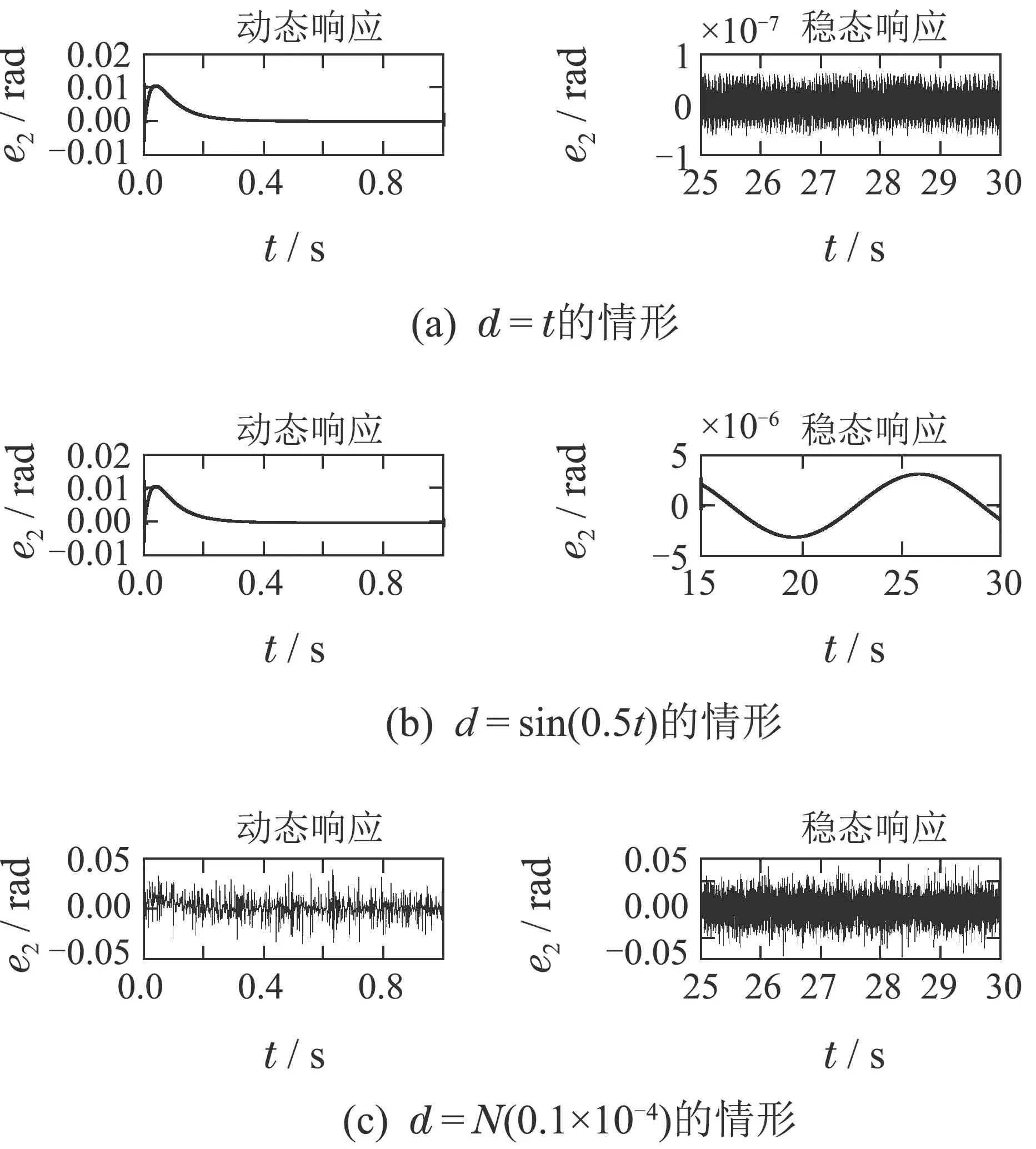
图8 大扰动情形经典方法对准精度Fig.8 Classical method alignment accuracy under large disturbance

注3在实际跟踪控制系统中还会受到传感器分辨率、探测噪声、执行机构控制噪声等多种客观因素影响,本文主要研究控制系统在动态性能方面的优化方法,未将以上因素带入仿真模型.

由图6和图8对比可以看出,在3种情形下,采用参数化控制方法能够达到的跟踪精度均要远远高于采用经典控制方法.

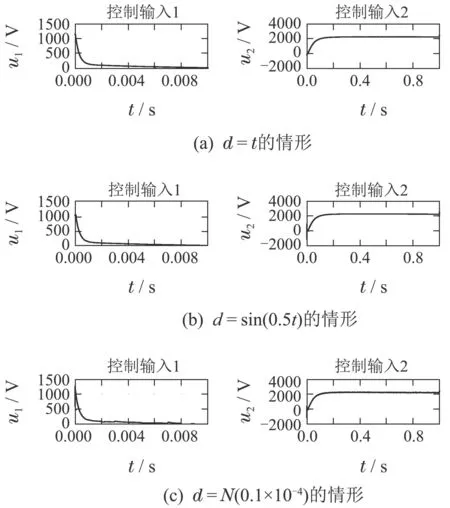
图9 大扰动情形经典方法控制输入Fig.9 Classical method control inputs under large disturbance

1)在以上3种情形下,采用参数化控制方法,角度的跟踪精度均可以达到10−9rad数量级.

2)在干扰选取为斜坡、正弦、白噪声这3种信号的情形下,采用经典控制方法,角度的跟踪精度分别只能达到10−7rad,10−6rad,10−2rad数量级.

注4根据文献[1],经典控制方法是对斜坡干扰完全解耦的.但是由本文的仿真结果图8(a)可以看出,采用经典方法得到的跟踪误差稳态会存在高频的抖动,这是由Simulink的计算噪声所引起的.对比图6(a)和图8(a)可以发现,本文的方法对这种计算噪声更为不敏感.

由图7和图9对比可以看出:

1)在3种干扰下,参数化控制方法的控制输入u1,u2的峰值分别在102V,100V数量级.而经典控制方法的控制输入u1,u2的峰值则均要达到103V数量级.

2)由图7(c)和图9(c)对比可以发现,当干扰为白噪声时,经典方法的控制输入u2存在微小的高频抖动,而参数化方法的两个控制输入均十分平稳.

可见,本文设计的参数化方法的控制效果在对准精度、干扰抑制能力、控制量峰值等方面要远远优于传统的控制方法.

5.3 小扰动情形

实际工程上,干扰的量级要小得多,可被归纳为如下3种情形:

情形1斜率为0.017的斜坡信号;

情形2幅值为0.0034,角频率为0.5 rad/s,初相位为0的正弦信号,即

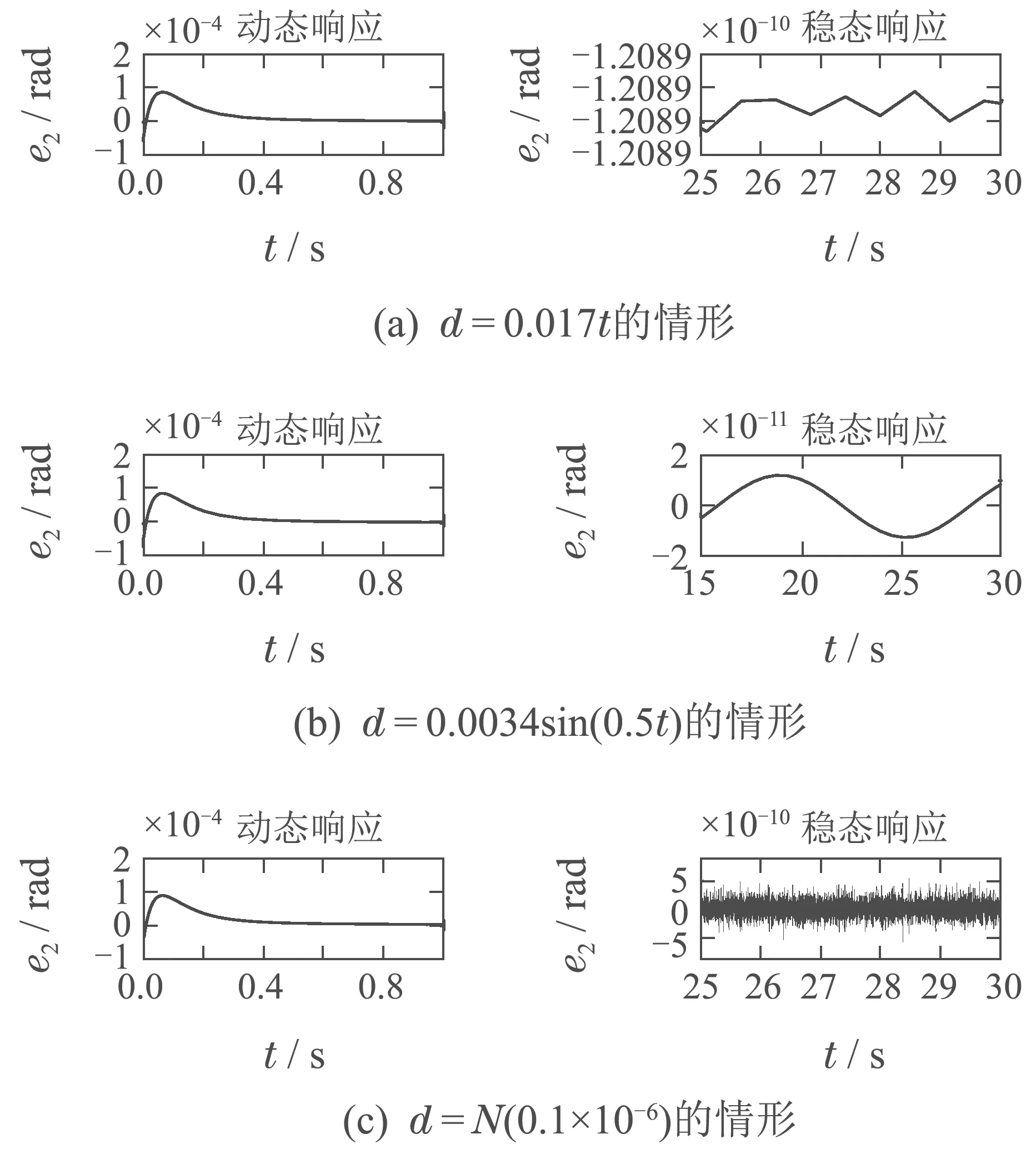
图10 小扰动情形参数化方法对准精度Fig.10 Parameterization method alignment accuracy under small disturbance

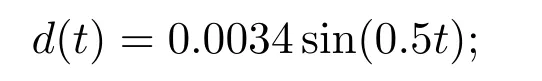
情形3方差为1×10−6的高斯白噪声(生成信号的步长为0.001 s).

在相同的仿真环境下,选取相同的初值,得到的以上3种情形的e2的响应曲线如图10所示,控制输入u1,u2的曲线如图11所示.

同样,针对经典控制方法也进行了相应仿真,采取与第5.2节经典控制方法相同的仿真环境与初值,得到的e2的响应曲线如图12所示,对应的控制输入u1,u2的曲线如图13所示.

由图10和图12对比可以看出,在将干扰选取为工程上的量级后,采用参数化控制方法能够达到的跟踪精度依旧均要远远高于采用经典控制方法.

1)在干扰选取为斜坡、正弦、白噪声这3种信号的情形下,采用参数化控制方法,角度的跟踪精度分别可以达到10−10rad,10−11rad,10−10rad数量级.

2)在干扰选取为斜坡、正弦、白噪声这3种信号的情形下,采用经典控制方法,角度的跟踪精度分别只能达到10−7rad,10−8rad,10−3rad数量级.

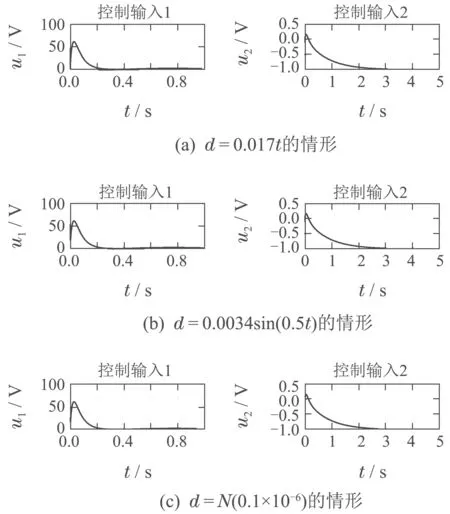
图11 小扰动情形参数化方法控制输入Fig.11 Parameterization method control inputs under small disturbance

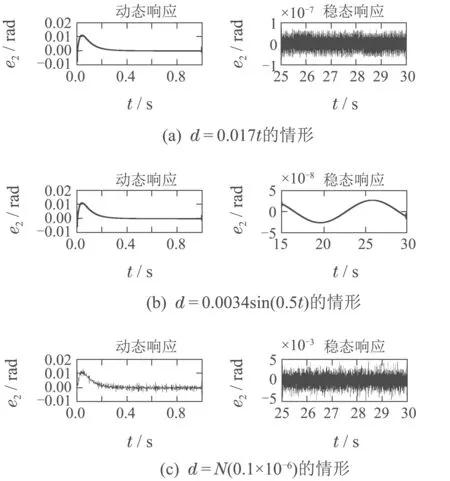
图12 小扰动情形经典方法对准精度Fig.12 Classical method alignment accuracy under small disturbance

由图11和图13对比可以看出,在3种干扰下,参数化控制方法的控制输入u1,u2的峰值分别在102V,100V数量级.而经典控制方法的控制输入u1,u2的峰值则均要达到103V数量级.

可见,本文设计的参数化方法的控制效果在对准精度、干扰抑制能力、控制量峰值等方面要远远优于传统的控制方法.

6 结论

本文研究了卫星光通信精确跟踪控制系统的设计问题,提出了一种参数化设计方法.在中国科学院空间科学战略性先导专项项目的支持下,我国在对空间尺度量子通信中低损耗链路实现的关键技术取得重大突破.该项目基于经典随动系统理论方法,实现了高精度捕获跟踪与瞄准系统圆满完成了空间量子科学实验任务.未来通信将向万公里及远距离发展,为了满足链路效率,信号发散角将降低一个数量级,相应对控制精度要求有数量级的提升,已有的传统的控制方法将难以满足.因此,本文开发了一种新的参数化控制系统设计方法.不同于传统的控制方法,参数化方法抛弃了传统的精、粗系统分别设计的思想,通过首先建立控制律的完全参数化表示,然后综合优化控制律中的自由参数来实现控制系统的多目标设计要求,因而相较于传统设计方法更加灵活方便,且更具整体性.本文设计的控制律同时考虑了精度、阶跃干扰解耦、干扰抑制、对参数摄动不敏感、控制增益等方面.从仿真结果上看,本文设计的参数化控制系统在对准精度、干扰抑制能力、控制输入峰值等方面要远远优于传统的控制方法.在本文中,系统的闭环极点并未参与优化,在之后的工作中可以令闭环极点同样参与优化.从而达到更好的控制效果.

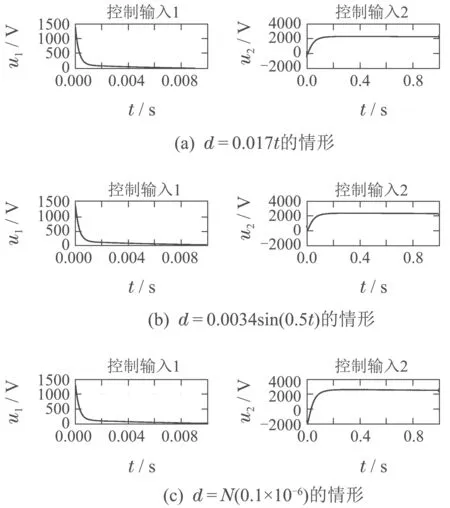
图13 小扰动情形经典方法控制输入Fig.13 Classical method control inputs under small disturbance