一种含噪声不确定多输入多输出非线性时变系统的最优跟踪控制

张 超,姜天华,孙启鸣

(1.河南工学院电气工程与自动化学院,河南新乡 453003;2.鲁东大学交通学院,山东烟台 264025;3.南京林业大学信息科学技术学院,江苏南京 210037)

1 引言

在工业领域,被控对象通常具有不确定性、强耦合、大非线性、时变特性和测量噪声,如机器人系统、电力系统、航天器系统和车辆系统等.即使采用智能控制方法,如自适应控制[1]、模糊控制[2]、神经网络控制[3]和解耦控制[4],也很难确保良好的控制性能.因此,东南大学严洪森教授团队提出了多维泰勒网(multi-dimensional Taylor network,MTN)综合控制方案.由于其具有自学习、自组织和自适应的特点,MTN可自动辨识被控系统参数并根据系统变化进行自身调节.本文基于自适应MTN模型设计多输入多输出(multiple-input multiple-output,MIMO)多维泰勒网控制器(multi-dimensional Taylor network controller,MTNC)和多维泰勒网滤波器(multi-dimensional Taylor network filter,MTNF).

在实际应用中,由于易于调整和结构简单,无论是工业界还是学术界,PID调节都是一个活跃的研究领域.获取PID和类PID控制器参数的方法有:增益相位裕度法[5]、优化方法[6]、Ziegler-Nichol方法[7]和基于内模控制的方法[8].对于单输入单输出(single-input single-output,SISO)系统,使用既有调节技术就可得到满意的控制效果.然而,由于输入和输出变量之间存在耦合关系,由SISO系统推导的控制律不能直接扩展到MIMO系统.此外,在MIMO系统中,PID参数的数量将变得非常多.试凑法不足以在控制器性能和鲁棒性之间获得最佳折衷.随着解决控制对象不确定性和复杂性的智能控制技术的迅速发展,神经网络已成为实现自适应控制器的选择之一.一些神经网络模型和神经网络训练方案被应用于系统控制器的设计[9–10].例如,作为前馈控制器,Plett[9]深入讨论了神经网络如何学习模仿被控对象的逆.然而,神经网络参数训练耗时且易陷入局部最小;无系统化的方法确定网络拓扑结构.

针对这些问题,设计规范的确定就显得尤为重要,即所采用的控制算法[11]和结构应足够简单且易于实现.设计的控制方案应包含非线性、鲁棒性、灵活性和学习能力等特征.目前一些学者正对MTN模型在模型预测[12]、系统辨识[13]、灾害预测[14]、电机控制[15]以及非线性控制[16−20]等领域的应用进行研究,但该模型仅应用于SISO系统且未综合考虑系统耦合、不确定性、时变特性及测量噪声等因素.同时研究发现,PID控制器是MTN控制器的特殊形式.此外,当采用固定步长的传统梯度下降法进行权值训练时,会存在收敛速度慢和局部最小值的问题[21].为此,在MTNC权值自适应调节过程中,针对被控对象的时变特性,设计线性再励的自适应变步长算法及自适应动量因子算法来解决.合适的参数不仅有利于平滑权值学习轨迹、加速算法收敛,而且有助于跳出误差曲面的局部最小值.

测量数据的消噪处理是分析和控制工业过程时不可或缺的处理手段.由于Lyapunov稳定性理论(Lyapunov stability theory,LST)能够保证稳定性,并且具有全局最小值的能量空间结构,因此在自适应滤波技术中得到了有效的应用.Man等[22]提出了基于LST的径向基神经网络(radial basis function neural network,RBFNN)的优化设计,实现有限脉冲响应(finiteimpulse response,FIR)自适应滤波器.但寻求最优RBFNN节点中心和高斯宽度的方法还未分析,其对于获得高滤波性能非常关键.同时,该结果只提供了Lyapunov滤波的基本思想,一些问题,如采用修正增益后的非线性滤波器的收敛速度和收敛区域尚待研究.因MTN具有任意逼近性和单中间层节点线性加权组合的简单计算,使得其成为构建非线性滤波器的选择之一.

本文利用MTN实现基于Lyapunov理论的自适应滤波(Lyapunov stability theory-based adaptive filtering,LAF)的无限脉冲响应(infinite-impulse response,IIR)自适应滤波器,设计了基于LST 的权值自适应算法以获得最优解.1)通过构建训练误差的Lyapunov函数V(能量函数),将LST应用到MTN权值训练算法;2)对权值进行重复更新以满足:∆V <0.根据LST,训练误差可指数收敛到零;3)分析LAF的误差收敛速度和改进LAF的误差收敛区域,避免“奇点”问题.

本文主要贡献为:1)进行MIMO MTN性能分析;2)推导MTNC权值的快速学习算法,给出MTNC权值的初始值选择方案;3)证明闭环系统的稳定性,并利用Lyapunov稳定性理论获得MTNC的稳定学习率;4)设计用于滤波的MTNF以消除测量噪声,并分析了滤波误差的收敛性速度和收敛区域.综上所述,MTNC和MTNF能够在不借助人工干预的情况下完成控制/滤波参数的调节,实现复杂被控对象优化跟踪控制.

2 问题描述

考虑MIMO非线性时变离散系统,可用输入输出差分方程表示为

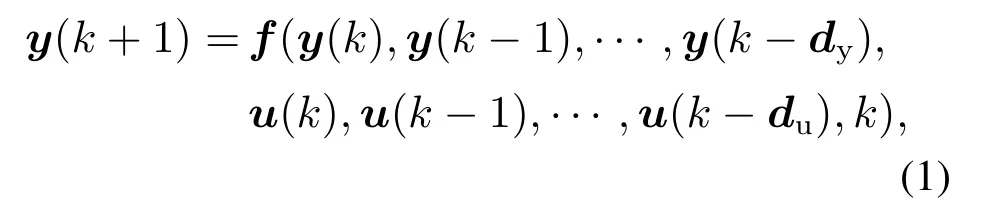
其中:

f(·)为非线性向量函数;

Rs为系统输出向量;

s表示输出的数量,j=1,2,···,s;

Rt为系统输入向量;

t表示输入的数量,i=1,2,···,t;k=1,2,···;

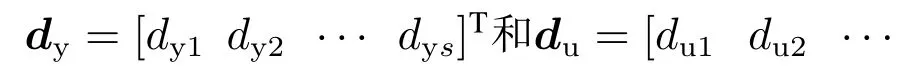
dut]T为相应的最大延迟.

如果被控对象所处的环境存在量测噪声(随机干扰),也就是被控对象受到噪声的作用,或者说被控对象受到噪声的污染,那么在式(1)中应加入相应的项,可得到

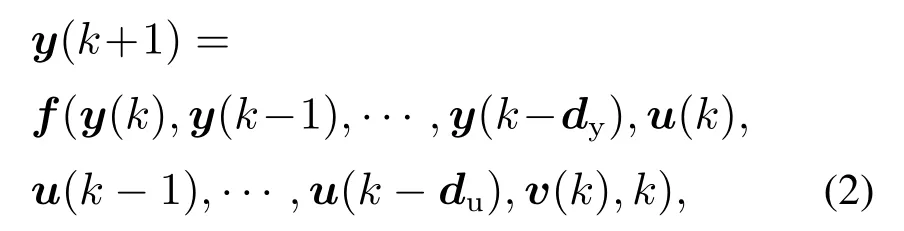
其中v(k)=[v1(k)v2(k)··· vj(k)··· vs(k)]T∈Rs为噪声向量,可以是模型噪声或测量噪声.含噪声非线性时变系统就是其扰动可以用随机过程表示的受控动力学时变系统.

3 多维泰勒网

3.1 模型描述

MIMO MTN模型具有结构简单、计算速度快的优点,其本质上是一个多项式类型的非线性自回归滑动平均模型.根据多元泰勒公式的原理,如果某函数在某点邻域处处m+1阶可导,则该函数在该点展开式为变量幂级数不大于m次的形式.因此,基于MIMO MTN模型,可以将n维系统的一般动力学方程表示为

其中:fi(·)表示用MTN模型描述的非线性函数,其基本思想是用简单函数逼近复杂函数;wip是第p个变量乘积项之前的权值;N(n,m)是该展开式的总项数;λp,q是第p个变量乘积项中变量xq的幂次.

如图1所示,多维泰勒网采用前向单中间层结构,包括输入层、中间层和输出层.只要N(n,m)足够大,MTN就能够以足够精度逼近任意模型[14].尽管式(3)是系统输入输出的非线性函数,但模型参数是线性关系的.同时,通过抽头延迟将系统的动力学特性引入到网络输入端,从而形成动态的网络化控制器.

3.2 性能分析

典型的离散PID控制器可以表示为

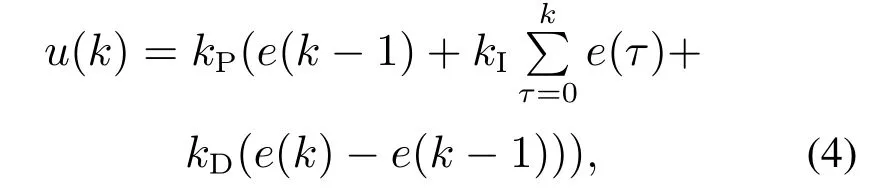
其中:u(k)为第k时刻的控制律;和kD分别为比例、积分和微分增益;TI和TD分别表示积分和微分常数;T表示采样时间.

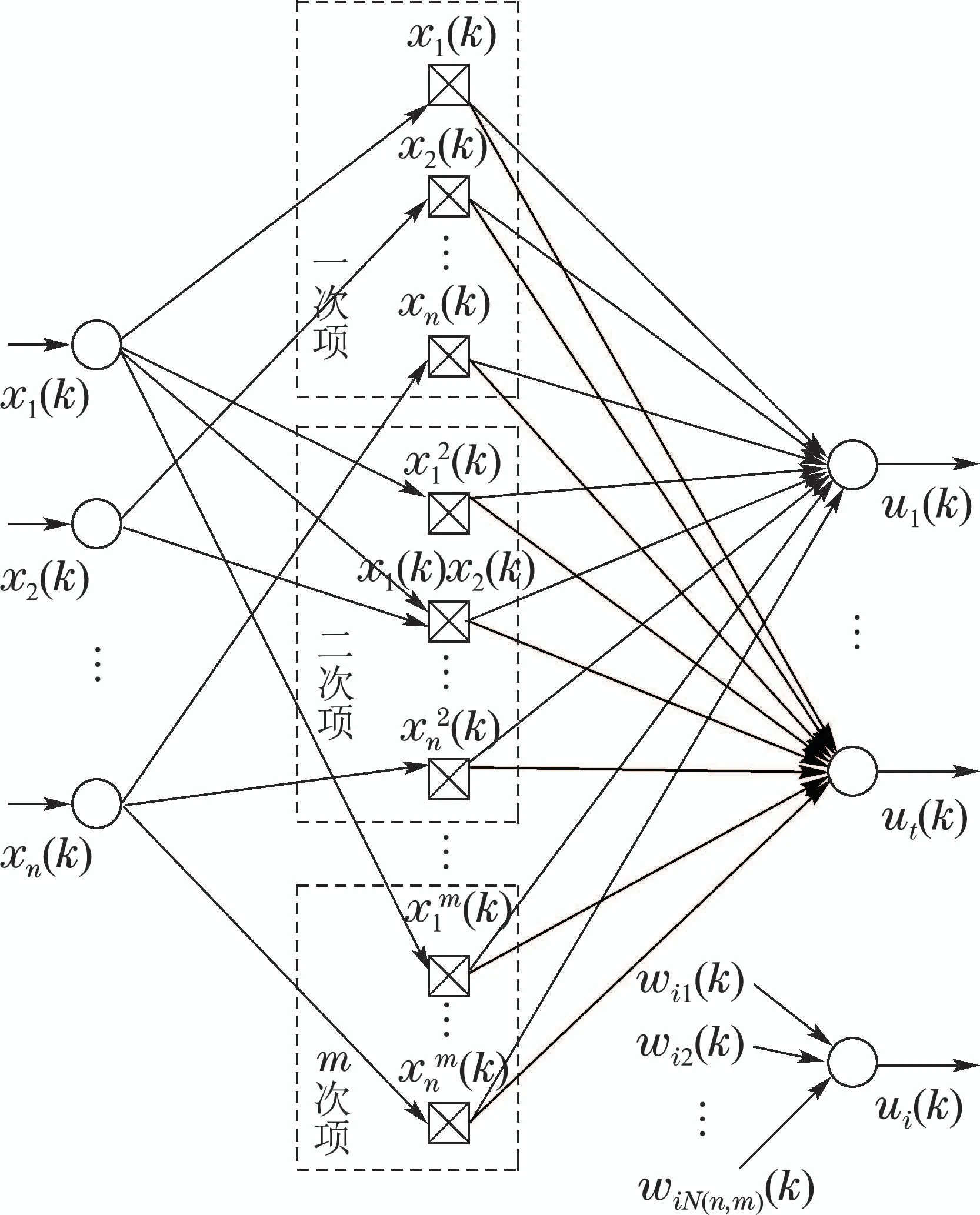
图1 多输入多输出多维泰勒网模型Fig.1 MIMO multi-dimensional Taylor network model

由式(3)可知,当n=3 且m=1 时,MTN控制器可以由向量形式表示:

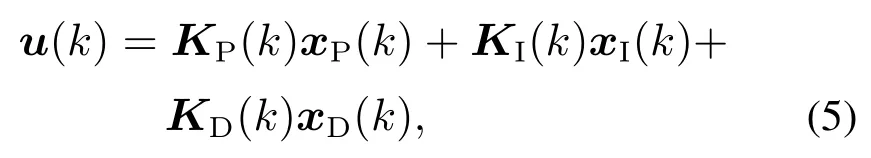
其中:xP(k)=[e1(k)e2(k)··· en(k)]T∈Rn,

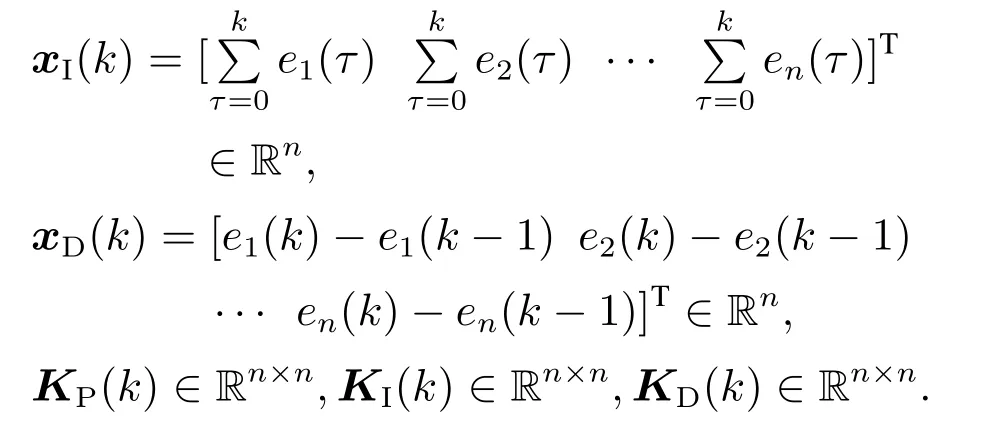
若KP,KI和KD选取为对角矩阵,结合式(4),PID控制器恰为幂次为1的MTN控制器的特殊形式;若KP,KI和KD选取为非对角矩阵,通过引入各通道之间的耦合实现了各子系统控制器参数的时变特性[16].

在工业应用中,如果选择的参数(kP,kI和kD)是最优的,就可得到满意的跟踪性能.然而,当系统具有强非线性、随机因素和时变特性时,选择这些参数是困难的.本文通过在线学习MTN 控制器参数,使得MTN控制器既具有经典PID控制简单的特点,又具有神经网络自学习能力强的优势.此外,根据理论分析[19]和仿真验证,MTN控制器高次项对动态性能改善效果显著.

4 MIMO MTN最优跟踪控制

4.1 控制系统结构

控制系统采用闭环控制,主要由控制器、被控对象和滤波器3部分组成,其中控制器和滤波器都是基于自适应多维泰勒网模型构建的,如图2所示.

在整个控制系统中,yd为目标矢量,eC为误差矢量,u为控制器输出的控制律,y为被控对象的输出,yv为受噪声污染的输出信号,ye为滤波后的输出信号.

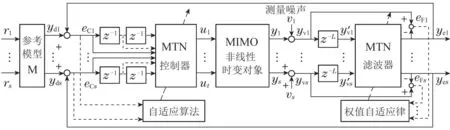
图2 基于MTN的控制系统结构图Fig.2 Structure of the control system with MTN proposed

4.2 自适应控制器参数调节

为了获得更好的控制效果并快速接近被控对象目标值,MTNC权值需根据误差进行调节,梯度下降法用于调整更新速度.对于函数f(u),u=(u1,u2,···,ut)T,梯度表示为

其中负梯度方向为最陡下降方向.动量项以一定概率加入到个体速度中,这有助于个体更有效地搜索解[23].权值更新方向是当前误差梯度和上一步权值更新增量的线性组合.合适的参数不仅有利于平滑权值学习轨迹、加快算法收敛,而且有助于跳出误差曲面的局部极小值.引入动量项的优点还有:1)当MTNC的误差曲面出现在平坦区域,动量项的引入将增加权值变化率并大大提高MTNC的收敛速度;2)当测量数据含有噪声等不确定因素,带动量项的权值更新算法通过限制权值更新方向的变化可提供低通滤波功能;3)对学习过程中的离群值和错误数据样本有一定的免疫力.

由此,MTNC权值由式(7)进行更新:

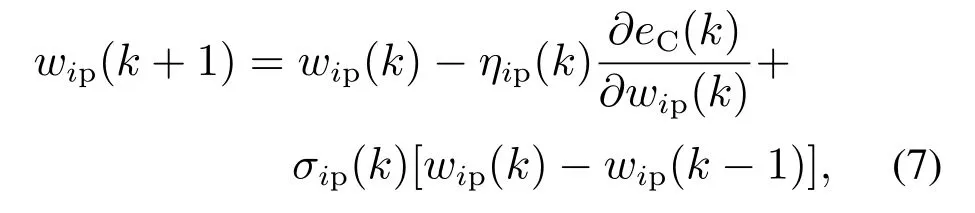
其中:η和σ为网络学习率;eC(k)为跟踪误差,计算如下:

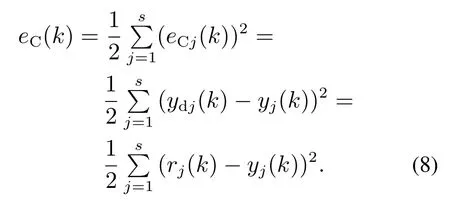
注1本节只关注自适应MIMO MTN控制器的设计,暂不考虑测量噪声的消除.同时,令参考模型M=I,其中I为单位矩阵,故yd(k)=r(k).

通过最小化跟踪误差eC(k)来自动调整权值,MTNC参数在每个采样周期内完成计算,实现被控对象的非线性、自适应实时控制.MTNC的权值更新规则为

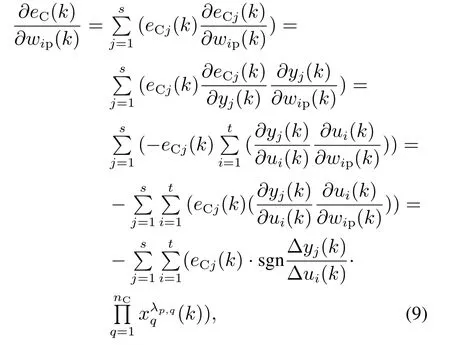
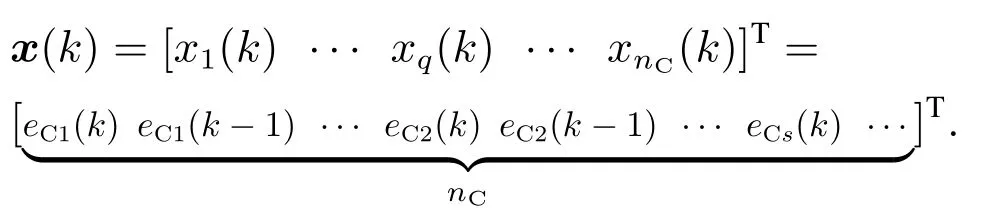
为了避免计算实际的结果,采用将梯度替换成符号的弹性BP算法来计算∆yj(k)/∆ui(k).这样既简化了计算,又满足了在线控制的要求,而且还大大避免了由于梯度太小而导致权值更新停止的问题.

此外,针对被控对象的时变特性,充分考虑MTN的特殊性,需对快速学习算法进行深入的研究和讨论.本节在MTNC学习过程中设计线性再励的自适应变步长算法和自适应动量因子.

1)线性再励的自适应变步长算法.

利用强化学习的理论[24],寻求自适应变步长算法,实现步长的自动选择,加快算法的收敛速度,减少迭代次数.强化学习是把学习看作试探评价过程,系统选择一个动作作用于环境,环境接受动作后状态发生变化,同时产生一个再励信号(奖或罚)反馈给系统,系统根据再励信号和环境当前状态再选择下一工作信号.

基于强化学习的自适应变步长算法表示为

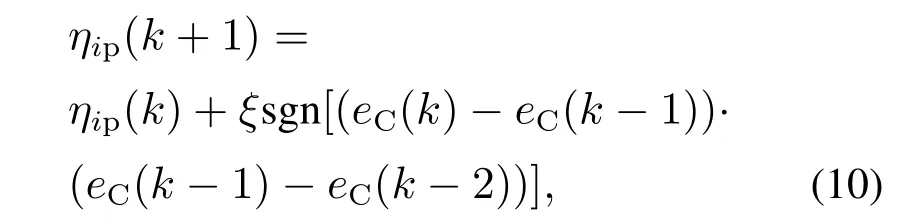
其中ξ为常数,其范围是0.001～0.003.本质上讲,该算法是利用并记忆梯度方向∆eC的符号变化信息,方向相反时对其罚,方向相同时对其奖.

2)自适应动量因子.

为了寻求加速收敛的方法,需在权值空间中考察梯度学习算法的误差曲面.在误差曲面的平坦区域,增大动量因子,可使权值更新向量wip(k+1)−wip(k)获得较大的冲量,有助于权值逃离误差曲面的平坦区域,从而加速算法收敛;在误差曲面的陡峭区域,减小动量因子可避免算法出现不稳定.因此,动量因子不能简单地取作常数,而应是自适应变化的.

误差曲面的陡缓程度可以用误差关于权值向量的梯度的范数来衡量:1)当梯度范数较大时,误差变化较快,误差曲面较陡;2)当梯度范数较小时,误差变化较慢,误差曲面平坦.

由此,动量因子可以根据误差关于权值向量的梯度大小自适应调节.其权值通过式(11)进行更新:

其中υ为正常数,用于控制动量因子的大小.显见,动量因子的取值范围是0～1,且随着误差关于权值向量的梯度范数的变化而变化.

4.3 闭环系统稳定性分析

在MTNC的学习过程中,由式(7)(10)和(11)组成的权值更新规则都需要选择合适的学习率η和σ.当η为较小的值时,尽管可保证收敛,但学习速度非常慢;当η取很大的值时,学习算法会变得不稳定.同时,在误差曲面的平坦区域,σ需足够大以加速算法收敛;在误差曲面的陡峭区域,σ又需恰当小以提高算法稳定性.为此,本节提出了稳定自适应学习率的选择方法.

定理1如果在采样时刻k,学习率ηip(k)存在η(k),动量因子σip(k)存在σ(k),且η(k)和σ(k)满足式(12)和(13),那么由图2表示的基于MTNC的闭环控制系统是稳定的.

证定义Lyapunov函数为

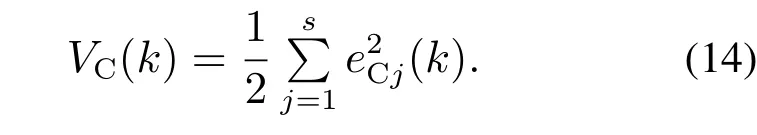
Lyapunov函数的变化为

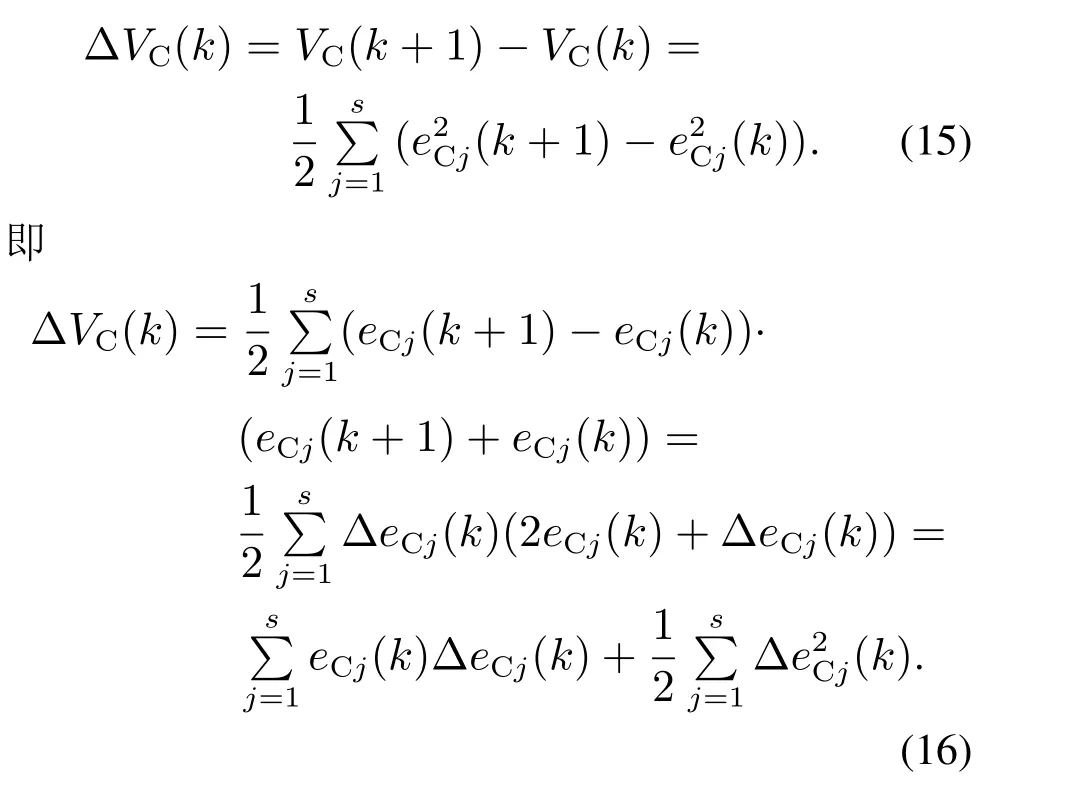
根据Lyapunov定理,如果在任何采样周期内都有∆VC(k)≤0则闭环系统是稳定的,则

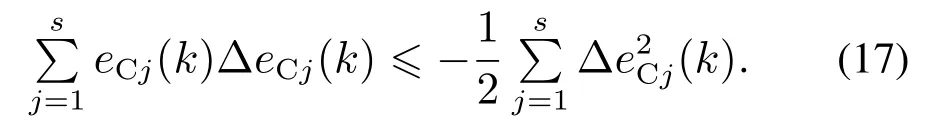
由式(7),可得

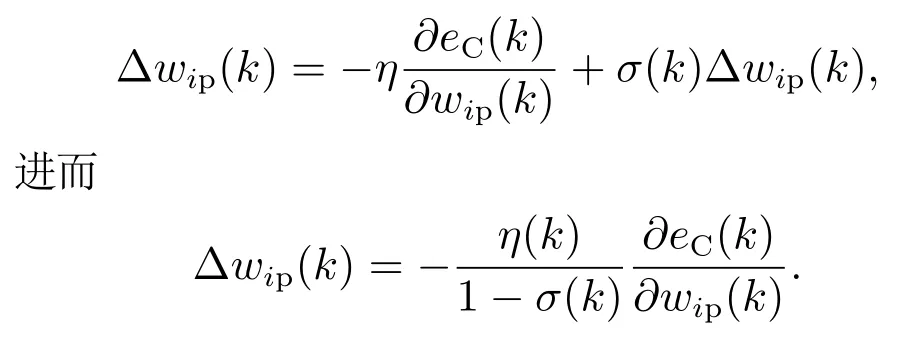
由式(8)–(11),可得

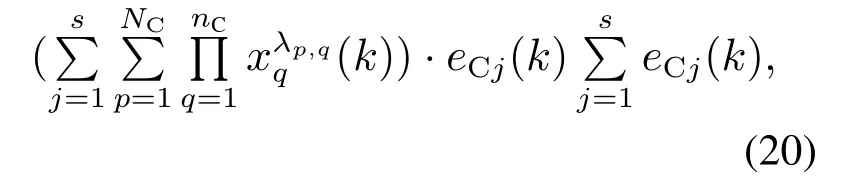
则式(19)可改写为

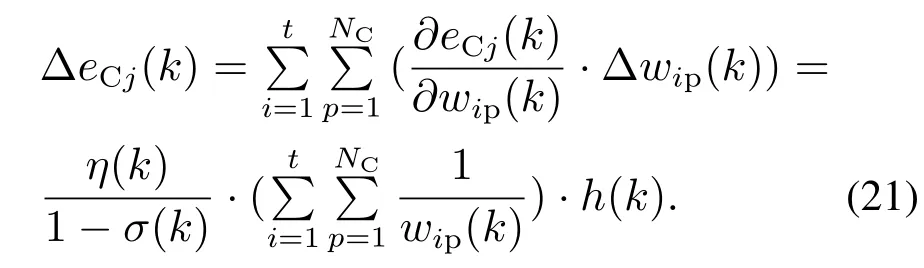
将式(21)代入式(17),可得

为确保∆VC(k)≤0,需分两种情况讨论:

由式(22),可以得出∆VC(k)≤0 的充分条件是η(k)和σ(k)满足式(23)和(24).同时,由式(23)和(24)可知,尽管需要计算wip(k)的倒数和h(k)的值,但其计算量很小.

5 MIMO MTN LAF滤波

5.1 基于MTN的自适应MIMO LAF IIR滤波器

本节实现了基于MTN的自适应MIMO IIR滤波器,其优点是MTN具有线性特性,通过LAF算法可以容易地调整网络参数.此外,MTN的并行结构也特别适用于快速信号处理.

滤波算法设计为自适应地更新滤波器参数,以使误差的目标函数在参数空间中最小化.由式(25)表示的eF(k)=[eF1(k)··· eFs(k)]T为期望响应和滤波器输出的误差;yv(k)=[yv1(k)··· yvs(k)]T为期望响应;ye(k)=[ye1(k)··· yes(k)]T为滤波器输出.

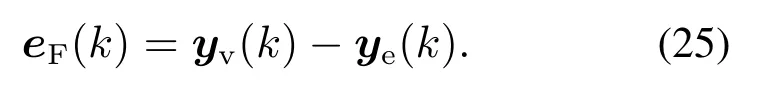
由于受到被控对象非线性和测量噪声的影响,MTN滤波器输入信号表示为

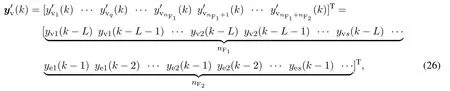
其中:L表示延迟数,nF1表示yv的输入个数,nF2表示ye的输入个数.

MIMO MTN IIR滤波器的输出可表示为

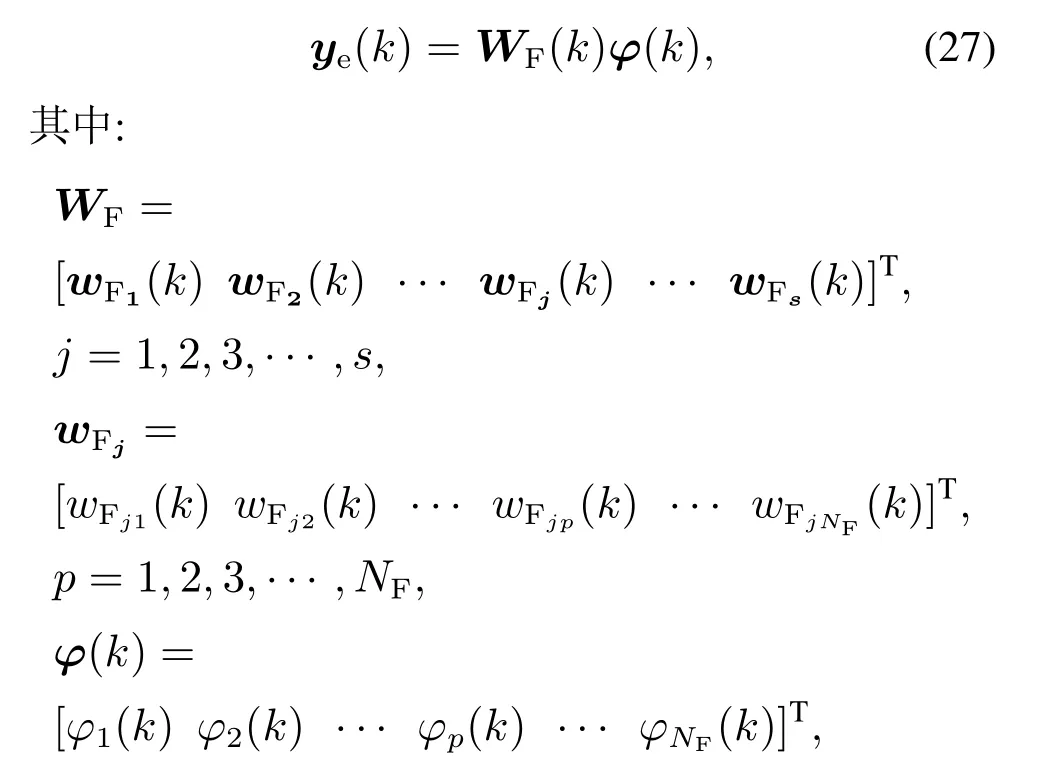
φ(k)是泰勒类型的函数,定义为

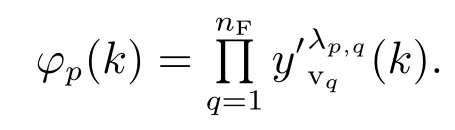
考虑量测过程输入输出关系为

其中:WFs×NF为待估计的MTNF参数矩阵;φ=[φ1··· φNF]T为量测向量;v=[v1··· vs]T为未知的系统量测噪声.

第k时刻,定义量测值和自适应MIMO MTN滤波输出之间的滤波误差为

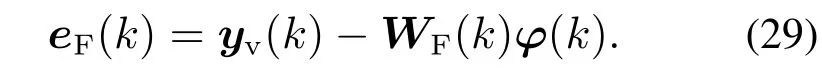
预测误差为

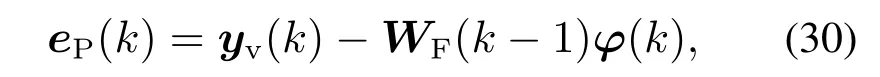
则以式(28)为量测方程的基于MIMO系统的LAF算法可定义为

为了防止当∥φ(k)∥和∥eP(k)∥趋近于零时增益K(k)出现奇点问题,式(32)被改写为

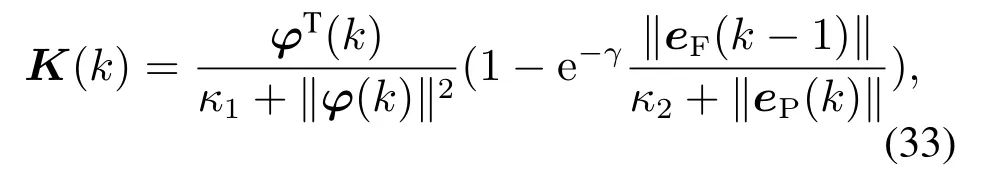
其中:K(k)为自适应增益;∥·∥为向量的欧氏范数;κ1和κ2为小的正整数;e−γ为自然指数函数,γ(γ≥1)为正常数,影响着算法的收敛速度,γ越大其收敛速度越快.

5.2 改进MIMO LAF算法的收敛性和稳定性分析

定理2当e−γ满足不等式(34),自适应MIMO LAF MTN滤波算法是稳定的.当MTN IIR滤波器权值由式(31)和(33)自适应更新,滤波误差将以指数收敛到以误差空间原点为中心、半径由式(35)定义的球体内.

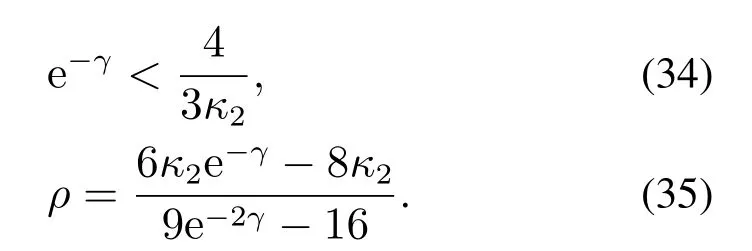
证定义滤波误差的Lyapunov函数:

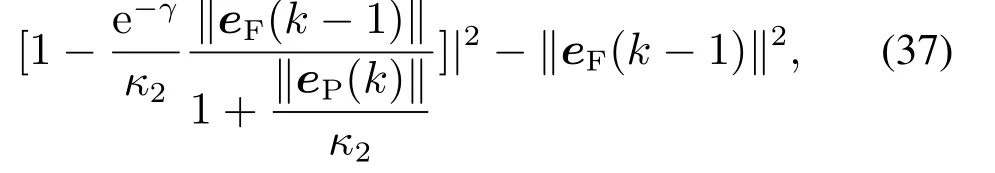
其中(∥φ(k)∥2/κ1)<1以及(∥eP(k)∥/κ2)<1.

泰勒级数展开应用于:

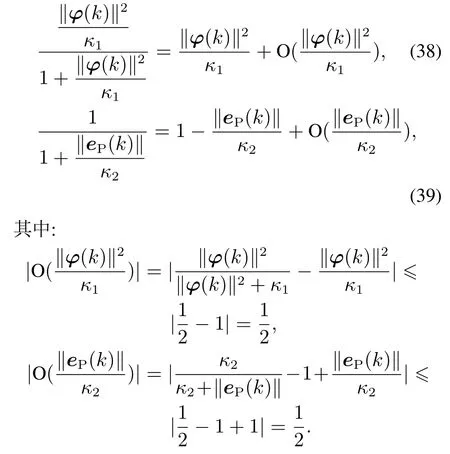
根据式(38)和(39),式(37)可改写为

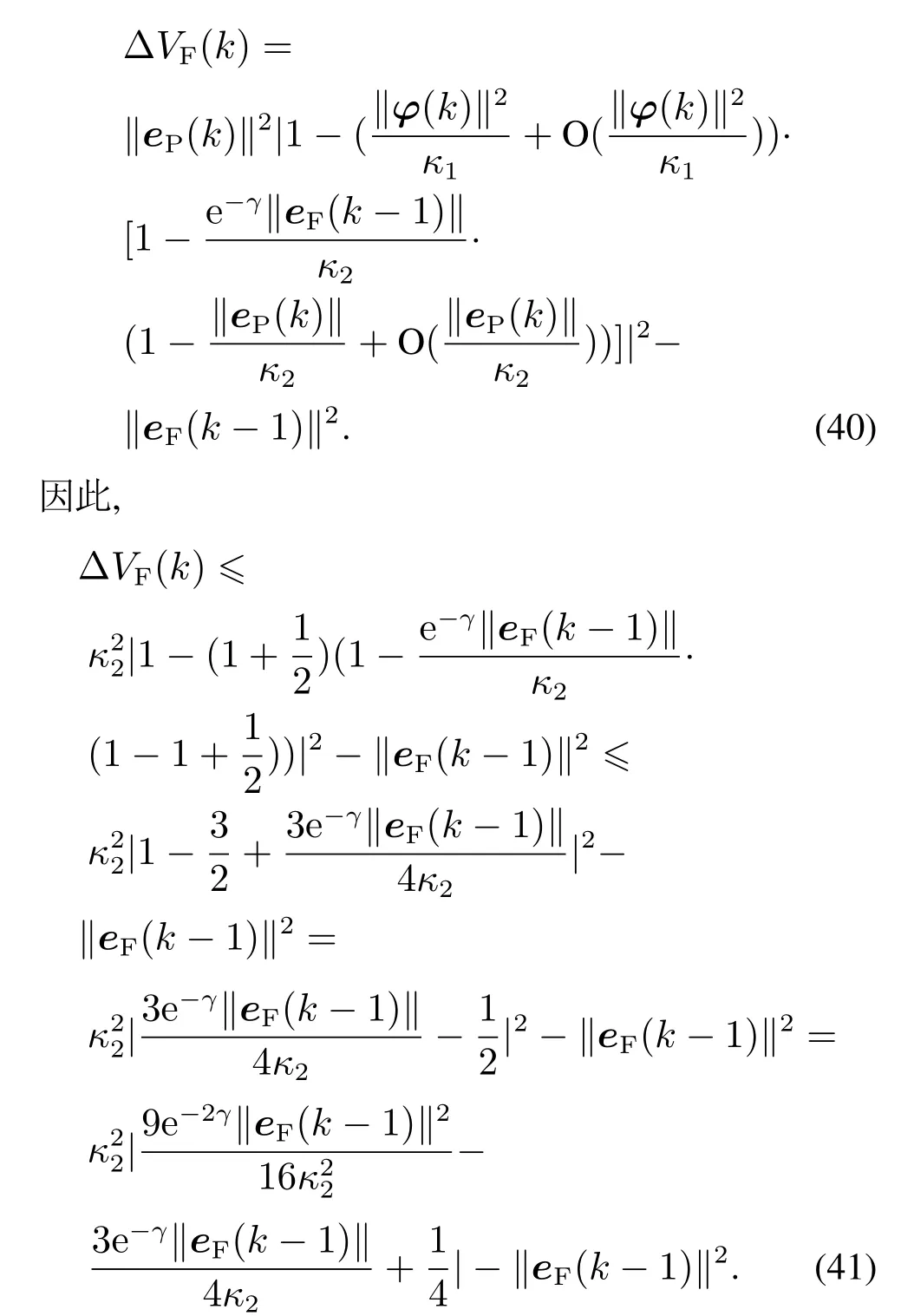
分两种情况讨论:

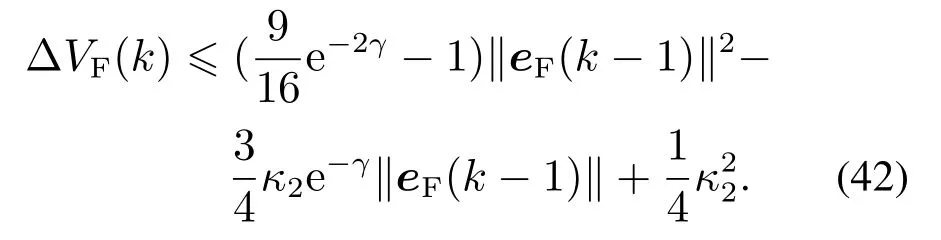
考虑抛物线函数

如果γ足够大(e−γ足够小),那么9e−2γ/16<1或3κ2e−γ/4<1.进 而,e−γ <4/3κ2且是向下凹的抛物线函数.此外,对于给定的κ1和κ2,参数e−γ满足下列不等式:

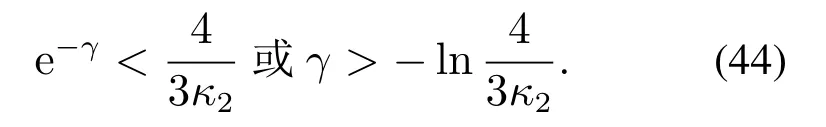
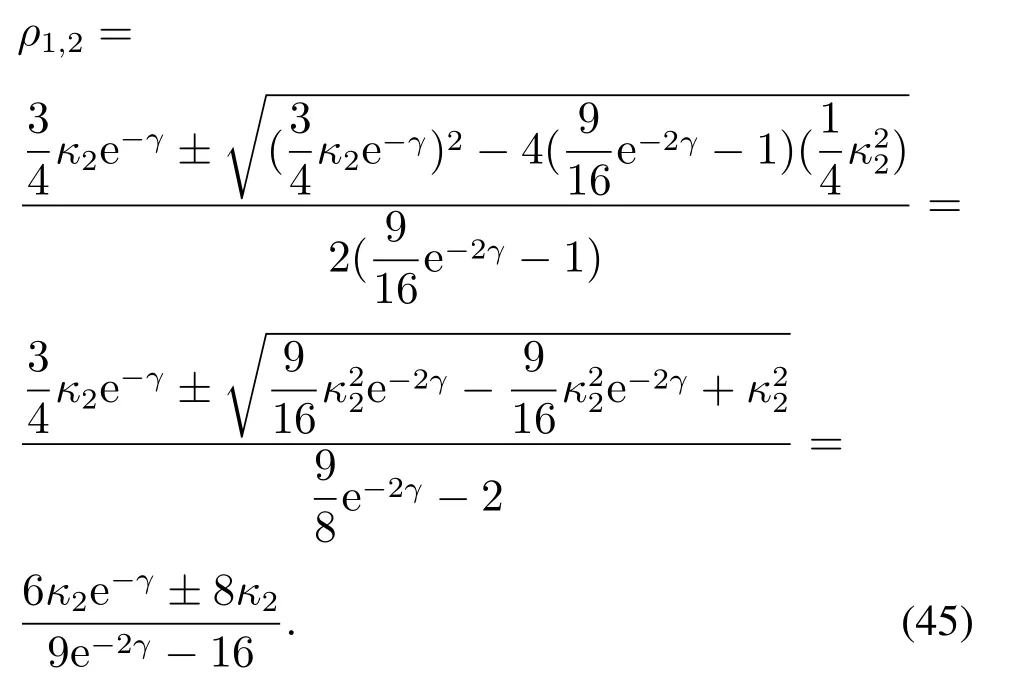
由于∥eF(k −1)∥≥0,只需考虑根ρ2,即

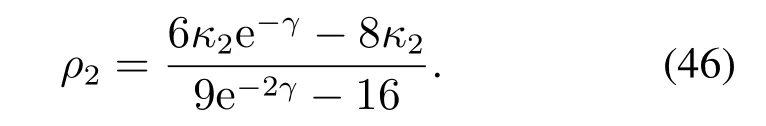
因此,∥eF(k −1)∥应满足以下不等式:

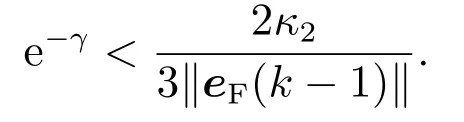
式(41)可以改写为

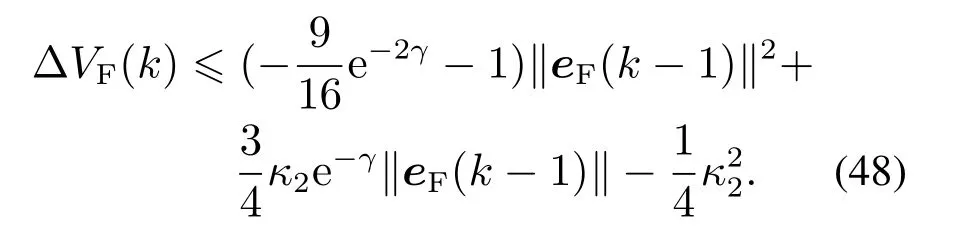
考虑抛物线函数:

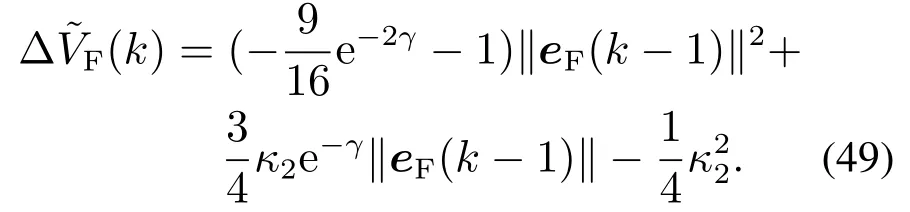
由 于e−γ >0,即(−(9e−2γ/16)−1)<0,那 么是向下凹的抛物线函数.此外,对于给定的κ1和κ2,因为

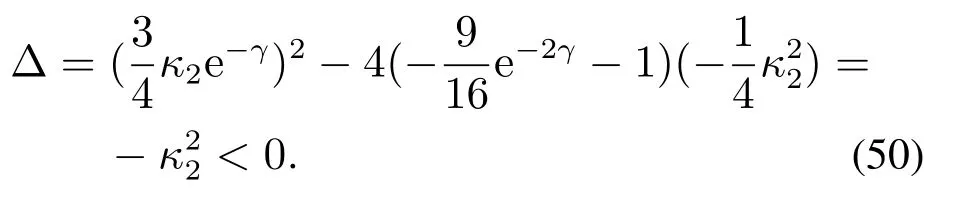
因此,在这种情况下无解(e−γ <((2κ2/3)·∥eF(k−1)∥)).

通过Lyapunov稳定性理论,定理2证明了自适应MIMO LAF MTN滤波系统的稳定性.随着迭代次数的增加,滤波收敛速度更快且滤波误差收敛到零.

6 仿真算例

被控对象为由式(51)表示的含测量噪声和强耦合变量的非线性时变系统:

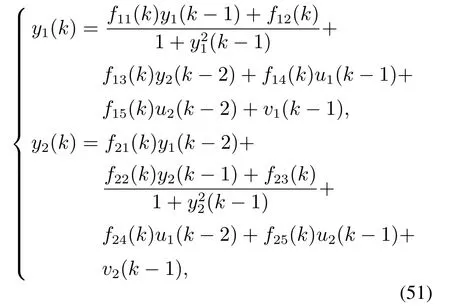
其中:u1和u2为控制律,

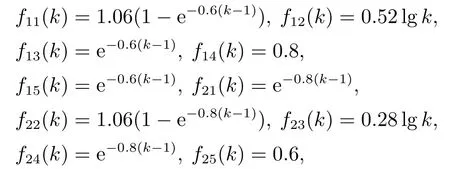
v(k)为均值为0、标准差为0.05的高斯白噪声.

为了表明MTN控制器和滤波器的有效性和优越性,分别将基于MTN和RBFNN[25]的控制方案作用于相同的被控对象,对控制性能进行分析和比较.两种方案实现时,只是用于构造控制器和滤波器的模型不同,自适应算法完全一致.系统参数设置如下:迭代次数50次;采样时间0.01 s;自适应MTNC参数:6–20–2结构,即6个输入节点、20个中间层节点和2个输出节点,其中nC=6,mC=2,初始学习率为0.01;自适应MTNF参数:6–20–2结构,即6个输入节点、20个中间层节点和2个输出节点,其中nF=6,mF=2.利用RBFNN建立控制器,6–27–2结构,即6个输入层神经元、27个隐层神经元和2个输出层神经元,采用线性再励的自适应变步长算法训练;利用RBFNN建立滤波器,6–27–2结构,采用改进的LAF算法训练.

图3给出了两种控制方案中实际输出值与目标输出值之间的对比.图4给出了随时间变化的控制律.

图3 两种控制方案的响应比较Fig.3 Comparison of response under different control methods

图5显示了随时间变化的跟踪误差比较.通过比较两种控制方案的上升时间,峰值时间和调节时间,相比于神经网络,MTN在解决时变自适应控制的问题上具有显著优势.

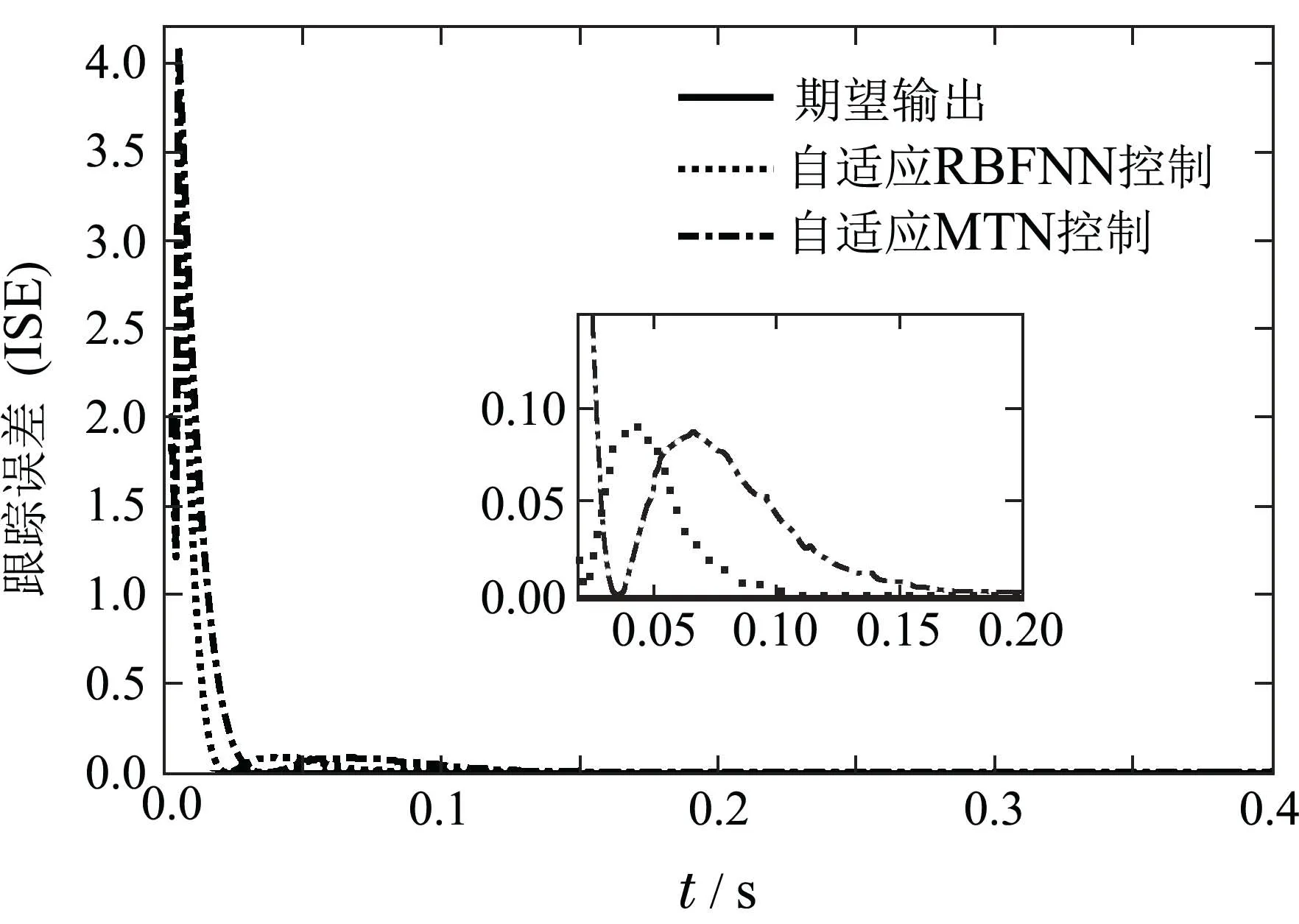
图5 跟踪误差比较Fig.5 Tracking error comparison

为了进一步比较两种控制方案的控制性能,从0.15 s内选择14组数据,表1列出了跟踪误差的具体值.结果说明实际输出值可通过基于MTN的方案更快速地逼近目标值.跟踪误差在0.02 s内下降得更快,并逐渐趋于0.控制律也迅速在短时间内变为常量.因此,对于复杂非线性系统,自适应MTN控制器和滤波器收敛速度快、精度高且稳定性好.

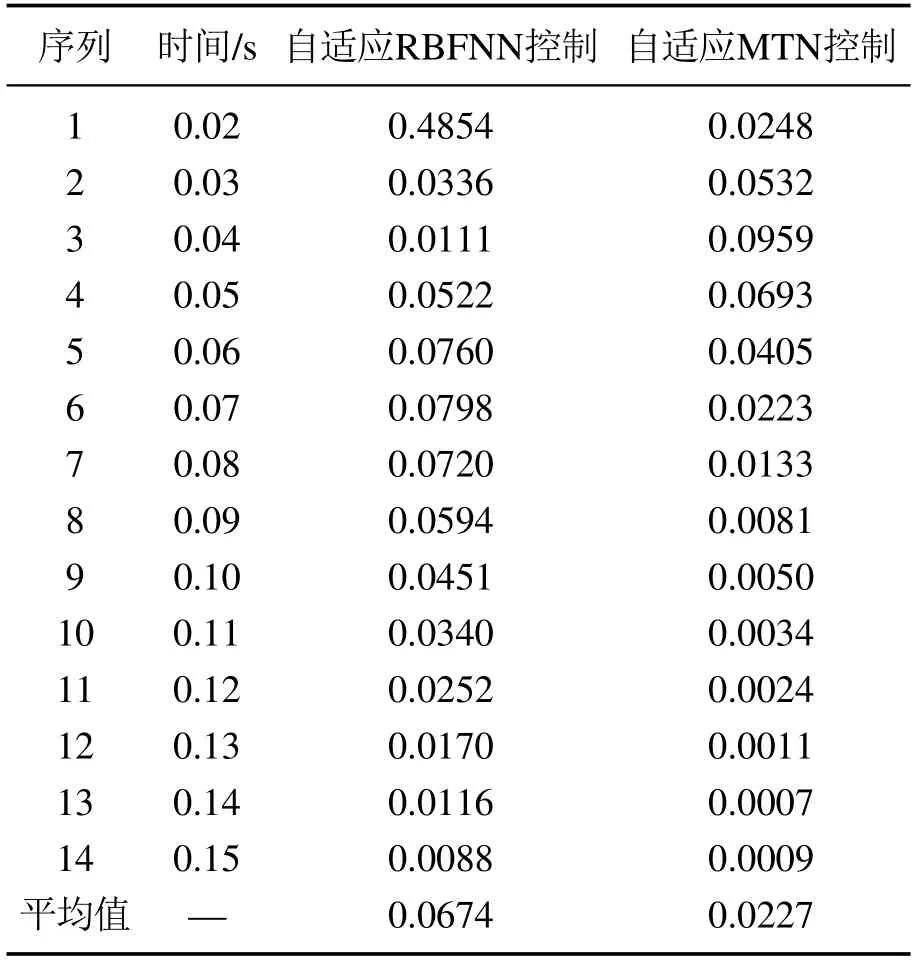
表1 两种控制方法的对比结果Table 1 Tracking error using above two control methods

7 结论

本文提出了基于自适应MTN的控制器和滤波器.一方面,在每个采样周期,设计基于强化学习和自适应动量因子的改进梯度法来更新MTNC权值;自适应参数调整具有自校正、在线和实时的特点;根据Lyapunov方法证明MTNC稳定性.另一方面,设计基于Lyapunov稳定性理论的MTNF权值改进更新算法,使动态误差指数收敛到零;基于改进LAF算法,证明MTNF误差的收敛速度和收敛区域,避免奇点问题.仿真结果表明自适应MTN控制器和滤波器可以在较少的采样周期内取得更佳的控制效果,误差稳定地趋于零.