地震作用下板式橡胶支座滑移对斜交桥受力特性的影响
李伟斌 董 晨 李楚涛
(江西理工大学,建筑与测绘工程学院,江西 赣州341000)
随着我国经济建设的快速发展,促使了大量桥梁的建设,而大部分的中小跨径桥梁都采用简支梁和连续梁桥的结构形式,而且几乎使用的都是板式橡胶支座。支座与上下构件的接触连接处并没有采取有效的固定方式,而是将支座直接放置于墩顶和主梁的钢垫板之间。简支桥由于上部结构整体性较差,故板式橡胶支座滑移在简支梁桥的抗震性能的影响效果更加明显[1]。
斜交桥由于其斜度的存在,使其具有独特的结构形式和受力特征,从而增大了桥面平动与转动的耦合,使得斜交桥在地震下的地震响应更加强烈,且较多发的震害是梁体的位移、桥面的旋转和梁端桥台的碰撞[2],目前研究支座连接方式对斜交桥影响的文献较少,因此本文研究分析地震作用下板式橡胶支座滑移是否加剧斜交桥的桥面的位移及转动。
目前,关于支座滑移对斜交桥的地震动力响应研究并不完善。范立础等[3]通过建立单墩模型对橡胶支座的滑移性能进行了参数研究。汤虎等[4]通过建立板式橡胶支座损伤判定准则,并对全桥模型进行非线性分析,以对典型板式橡胶支座简支梁桥进行抗震性能评价。项乃亮等[5]采用板式橡胶支座实体模型,对支座与钢板间的滑移性能进行了足尺试验,并建立板式橡胶支座与钢板间滑动摩擦效应的力学计算模型。项乃亮等[6]采用大比例全桥振动台试验,探究了不同墩梁约束体系下的地震效应特点。韩强等[7]通过分析汶川地震的桥梁灾害,提出了现有规范的不足,并要求对板式橡胶支座的隔震效应进行更加深入的研究。在大部分学者进行数值模拟分析时,都采取支座与主梁和墩台之间绑定或是在上下节点添加弹簧单元的简化方式进行数值模拟计算,忽略了板式橡胶支座的滑移效应对于结构整体抗震性能的影响,而当支座发生滑移时,由于桥梁抗震体系在地震作用下的传力路径被部分中断,使得结构的抗震性能将异于支座绑定的情况。
本文通过Ansys 建立典型的斜交简支梁桥有限元模型,对比分析了板式橡胶支座在上部结构和下部结构间可滑移与绑定这两种连接形式对斜交简支梁桥地震作用下的影响,以期为设置板式橡胶支座为减隔震装置斜交桥的减隔震设计及抗震方面的相关研究提供参考依据。
1 基本计算条件
1.1 计算模型
本文采用有限元软件Ansys 进行建模及计算,模型跨径32.5m,主梁为单箱双室斜交梁,桥面斜度为30°,梁高为1.9m,桥墩采用独柱墩,墩柱直径1.5m,墩高9m,全桥采用GYZ d400板式橡胶支座,其抗剪切刚度为3966kN/m,支座与上下接触面摩擦系数取0.2。成桥状态计算模型如图1 所示。

图1 有限元计算模型
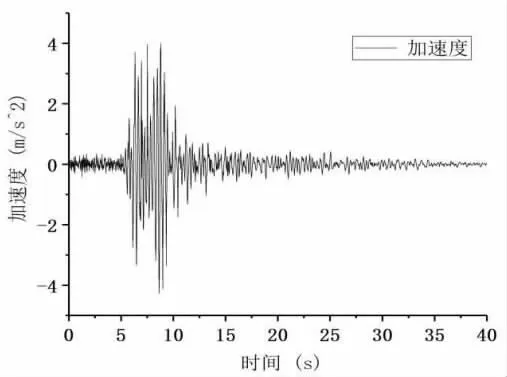
图2 地震波输入时程
1.2 地震波的选取与输入
本文选取1987 年10 月10 号发生于美国加利福尼亚的Whittier Narrows 地震,并将地震波峰值调幅至0.4g,其地震波输入时程如图2 所示。
在桥梁的抗震设计和抗震研究中,不同地震激励方向下结构的动态响应有所差异,对于几何形状不规则桥梁,地震输入方向对结构地震响应的影响不容忽视,斜交桥相对于正交桥,由于其复杂的受力特征,若仍像正交桥一样的方法输入,并不一定能得到最不利的地震响应,使计算结果存在偏差[8]。因此本文将采取从0°到180°之间每隔15°输入地震波的方式进行逐次计算,并将最大的地震响应量进行对比。
2 地震响应结果分析
2.1 墩低内力结果对比
由于地震作用下桥墩主要的震害有受弯破坏和剪切破坏两种典型形式,所以桥墩墩底内力成为判定斜交桥最不利输入角度的主要依据。如图3 所示,两种工况下地震响应峰值都出现在150°,支座滑移时的弯矩响应峰值为4932.3kN·m,而绑定支座时的弯矩峰值6392.7kN·m,后者要比前者增大29.6%,整体而言,不考虑支座滑移的弯矩要比考虑支座滑移的弯矩大9.6%~33.6%。
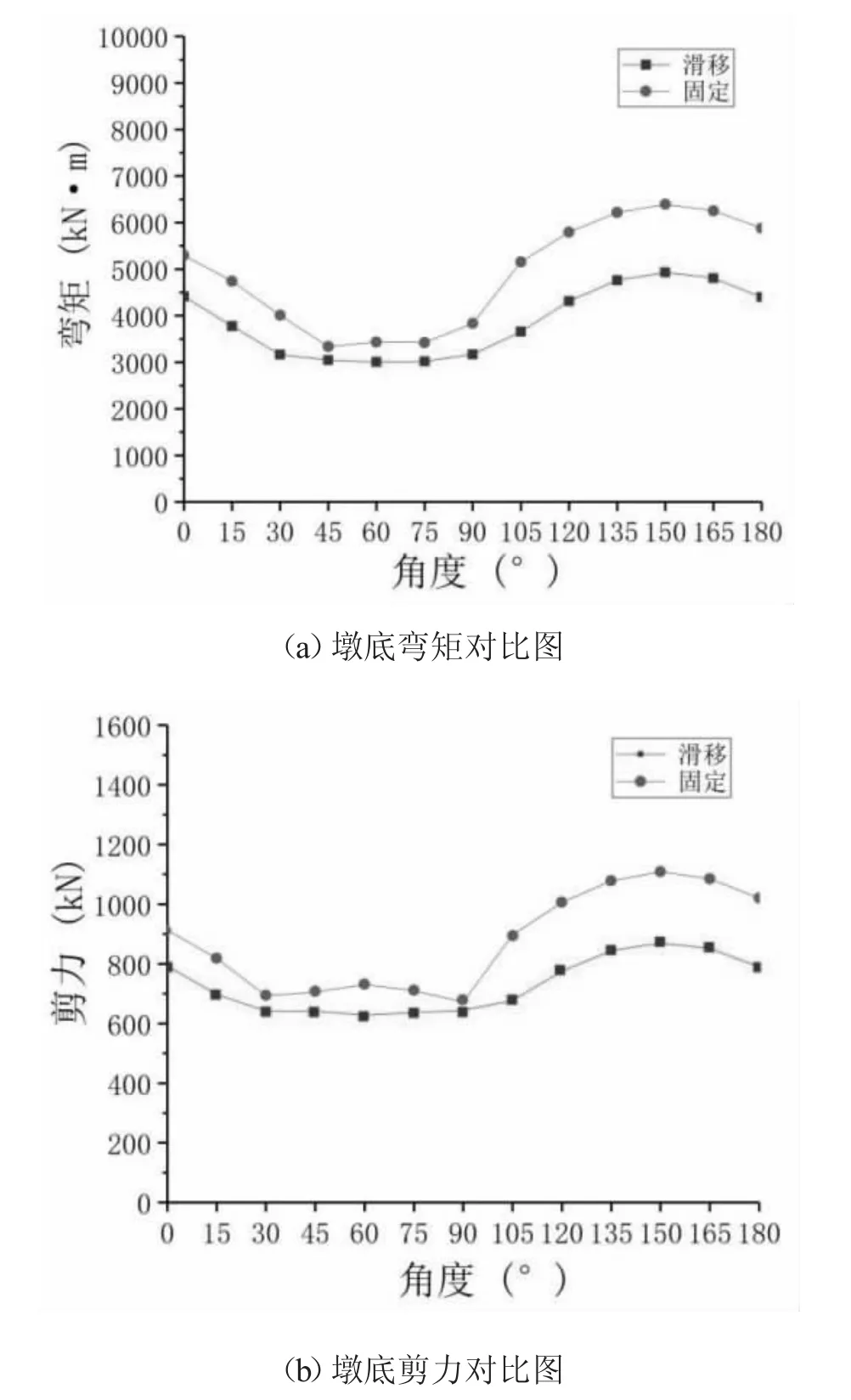
图3 墩底内力对比
两种工况下墩底剪力对比如图3b 所示,考虑支座滑移和绑定两种情况下两者的墩底剪力峰值都出现在了150°,其中考虑支座滑移的剪力响应峰值为870.4kN,而绑定支座的墩底剪力峰值为1108.5kN,后者比前者增大27.4%,绑定支座情况下的墩底剪力响应值整体上要比考虑支座滑移情况下的响应值大8%~32.2%。
从墩底内力对比结果可以看出,当考虑支座滑移时墩底内力响应明显要比绑定情况下的要小得多,这是因为在地震作用下支座可以通过滑移时的摩擦作用,有效地消耗掉一部分的地震能量,相应的减少了上部结构在地震作用下通过支座传递下来的水平荷载。
2.2 墩梁相对位移结果对比
墩梁相对位移逐次计算结果对比如图4 所示,两者墩梁相对位移的峰值都出现在150°,考虑支座滑移的墩梁相对位移峰值为0.0276m,绑定支座情况下的墩梁相对位移峰值为0.0405m 比前者增大46.6%,从整体而言,绑定支座情况下的墩梁相对位移要比支座滑移的大34.1%~46.6%,由此可见,支座滑移由于摩擦作用的存在,有效地耗散了地震能量,缩小了桥墩的相对位移。

图4 墩梁相对位移对比图
2.3 桥面旋转结果对比
桥面旋转角度θ 如图5 所示,通过桥轴线与主梁端的夹角β 和桥轴线与盖梁夹角α 之差进行表示即θ=|βα|。

图5 墩梁夹角示意图

图6 墩梁相对夹角对比图
两种设置情况下的桥面旋转结果对比如图6 所示,考虑支座滑移的桥面旋转角度峰值为0.0049°,支座绑定的桥面旋转角度峰值为0.0021°,前者在逐次计算中的桥面旋转值基本维持在0.0044°~0.0049°之间,而支座绑定的桥面旋转值基本维持在0.0016°~0.0021°之间,虽然两者的旋转角度并不大,但是当桥面宽度达到一定程度,和考虑碰撞的影响,其位移影响将被放大。支座绑定的桥面旋转值相应要比考虑支座滑移的值小57.1%~63.6%。在发生较强烈的地震时,若是与相邻结构的间距小于其位移量,将会发生桥端碰撞,而桥面旋转会影响斜交桥钝角及锐角的位移量,有可能加剧梁端的碰撞效应,引起更大的桥面旋转[9]。
3 结论
本文通过建立考虑支座滑移和绑定支座两种支座设置情况下的斜交桥模型,并计算分析了斜交桥支座滑移和绑定支座这两种情况在地震作用下的地震响应,主要结论如下:
(1)在地震作用下,考虑支座滑移和绑定支座两种支座连接形式在墩底内力和位移的响应量峰值都出现在150°,由此可见支座的滑移与绑定并不会影响斜交桥最不利输入方向的确定。
(2)通过对两者地震下墩底内力的结果对比可知,考虑支座滑移情况下的弯矩和剪力都要明显的小于支座绑定的情况,说明支座滑移通过摩擦的形式,可以有效的耗散地震能量,减小上部结构惯性力的传递,以达到支座减震的效果。同时若是忽略支座的滑移,必将对桥梁的设计造成影响,使其设计结果偏于保守,造成资金及资源不必要的浪费。
(3)考虑支座滑移的墩梁相对位移明显要比支座绑定情况下的响应小得多,但转角前者要比后者大,当考虑梁端碰撞效应时,也许碰撞和转角将发生耦合作用,从而使斜交桥位移和转角加大。

