一种用于图像检索的幂归一化深度卷积特征加权聚合方法
张 琴,伍世虔,徐望明,4
(1.武汉科技大学机械自动化学院,湖北 武汉,430081;2.武汉科技大学机器人与智能系统研究院,湖北 武汉,430081;3.武汉科技大学信息科学与工程学院,湖北 武汉,430081;4.武汉科技大学冶金自动化与检测技术教育部工程研究中心,湖北 武汉,430081)
基于内容的图像检索(content-based image retrieval,CBIR)[1-5]一直是计算机视觉研究领域中的热门课题。它通过特征提取算法将图像表示为向量,并利用近邻搜索方法找到与给定的查询图像内容相似的图像,其中,特征提取算法对图像检索性能起着关键作用。为了提取出具有判别能力的图像特征,形成有效的图像表示,人们针对特征提取算法进行了大量研究,近十几年来其经历了从基于SIFT[6]、SURF[7]等算法并结合BOW[8-9]、FV[10]、VLAD[11]等嵌入编码方法提取图像浅层特征到基于深度卷积神经网络[12]提取图像深层特征的发展过程。
最近研究表明,在图像检索任务中,采用在大规模数据库ImageNet[13]上预训练好的卷积神经网络提取的深度特征比传统的浅层特征取得了更加好的检索效果[14-19],而且深度网络中卷积层[17-22]输出的特征可看作图像的局部表示,能体现出更多的图像细节信息,比全连接层[14-15]输出的特征取得了更高的检索精度。因此,目前的主流算法是将卷积层输出的特征进行聚合形成图像的全局表示。卷积层的特征聚合又分为两种:一种是编码聚合[16-18],这种方法将卷积层的列特征看作类似于SIFT的局部特征,进行VLAD、FV或BOW等嵌入编码,最后聚合成图像的全局表示;另一种是直接聚合[19-22],将卷积层的特征图直接求和聚合或加权后求和聚合,形成图像的全局表示。
深度卷积特征比经典手工局部特征具有更强的判别能力,而且适用于经典SIFT特征的嵌入编码方式不宜简单移植到深度卷积特征上,直接对深度卷积特征进行求和聚合,可取得比常用编码聚合方法更好的性能[19],因此本文着重研究深度卷积特征的直接聚合方法。对于典型的聚合方法——基于部位的加权聚合(part-based weighting aggregation,PWA)方法[22],笔者发现,聚合后的特征在大部分维度上的响应比较小,而在一小部分维度上的响应却明显较大,这隐含着类似于基于SIFT的浅层编码特征出现的视觉突发(visual burstiness)问题[23],即图像特征中某些元素信息多倍于其它元素信息重复出现,这些重复的视觉特征在进行图像相似性度量时会起主导作用,使得图像检索精度降低。为了有效调节这种视觉突发效应,改善图像检索效果,本文运用幂归一化方法改进PWA特征聚合方法,并在4个标准的图像数据库上进行图像检索实验,以验证改进方法的有效性。
1PWA特征聚合方法及其存在的问题
一般而言,深度卷积特征的聚合方法是将卷积神经网络的卷积层输出的特征图作为聚合算法的输入,可用3维张量表示为X∈RK×W×H,这里W×H表示空间分辨率,K表示特征图数量或通道数量,其中一个通道对应的特征图为二维矩阵Xk∈R(W×H)(k=1,2,…,K),该特征图中的一个元素表示为Xk(i,j)∈R(i=1,2,…,W;j=1,2,…,H)。
深度卷积特征聚合方法的典型代表是基于部位的加权聚合(PWA)。文献[24]中指出:深度卷积神经网络卷积层中特定通道对特定语义有较强的响应,一些具有区分性的通道可用来作为目标的部位检测器(part detector)。受此启发,文献[22]提出PWA框架,先从深度卷积神经网络卷积层输出的所有通道中选出一部分有代表性的具有区分性的通道作为包含特定语义的部位检测器,用作空间权重,再对该层输出的所有卷积特征图(通道)进行加权聚合,形成具有特定语义的区域聚合特征,然后将这些区域特征连接起来即可形成最终的图像全局表示。
PWA方法中具有区分性的通道是根据待检索图像数据库中所有图像样本的通道特征图的聚合值的方差来选择的,方差越大则该通道特征图的区分性越强,该过程可以离线完成。第m幅图像在卷积层输出的第k个通道特征图的求和聚合值为:
(1)
设图像数据库一共有M幅图像,则第k个通道特征图的均值为:
(2)
那么第k个通道特征图的方差为:
(3)
对所有方差dk(k=1,2,…,K)排序,选择其中最大的N个方差所对应的通道作为部位检测器。
将选取的N个通道特征图表示为X(n)∈RW×H(n=1,2,…,N),则空间权重Sn(i,j)的产生方式可表示为:
Sn(i,j)=
(4)
式中:a和b均为幂变换参数。用该空间权重对第k个通道特征图加权求和:
(5)
这样,利用K个通道的加权求和特征值可构成特征向量
Fn=[fn,1,fn,2,…,fn,K]
(6)
形成区域聚合特征,然后将N个区域特征连接起来,即形成PWA图像全局特征表示:
Fpwa=[F1,F2,…,FN]
(7)
(8)
式中:D为最终特征的维度;P为PCA降维矩阵;σ1,σ2,…,σD为与P相关的D个奇异值。
由于PWA特征包含了语义信息,故在图像检索任务中取得了现阶段较好的效果。然而如前所言,这种PWA特征可能出现视觉突发现象,影响图像检索精度。
以图1为例,图1(a)是Oxford5k图像数据库[25]中的一幅查询图像(图中黄色框内的建筑物窗户),图1(b)和图1(c)是该库中的两幅参考图像,其中图1(b)不包含查询区域,图1(c)包含查询区域。图1(d)~(f)分别表示图1(a)~(c)的PWA聚合特征响应。从图1(d)~(f)中不难发现,原PWA聚合特征的响应值在少数特征维度上取值特别大,而大部分特征维度上的响应值却相对很小;同时也容易观察到图1(d)与图1(e)中响应取较大值的位置十分相似,而图1(d)与图1(f)却有明显区别。实验发现,通过欧氏距离进行特征相似性度量,图1(a)和图1(b)的相似性大于图1(a)和图1(c)的相似性,表明这些少数很大的响应主导了图像的相似性度量,导致图像检索精度降低。
(a)查询图像(框中区域) (b)参考图像1(c)参考图像2
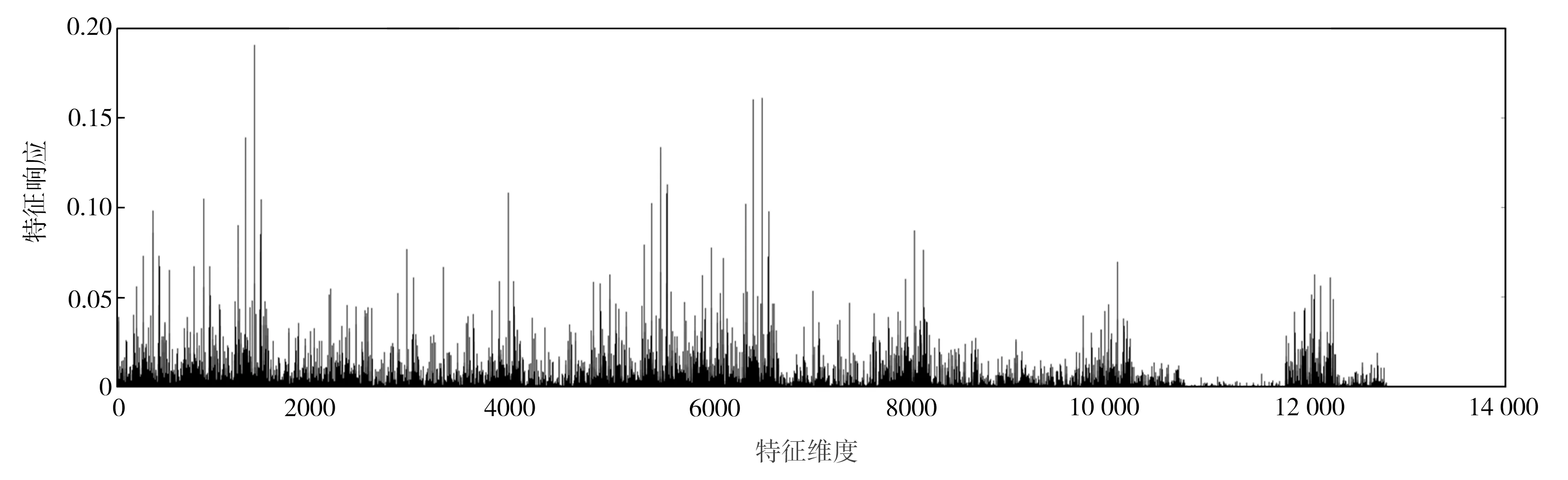
(d)查询图像的PWA特征响应
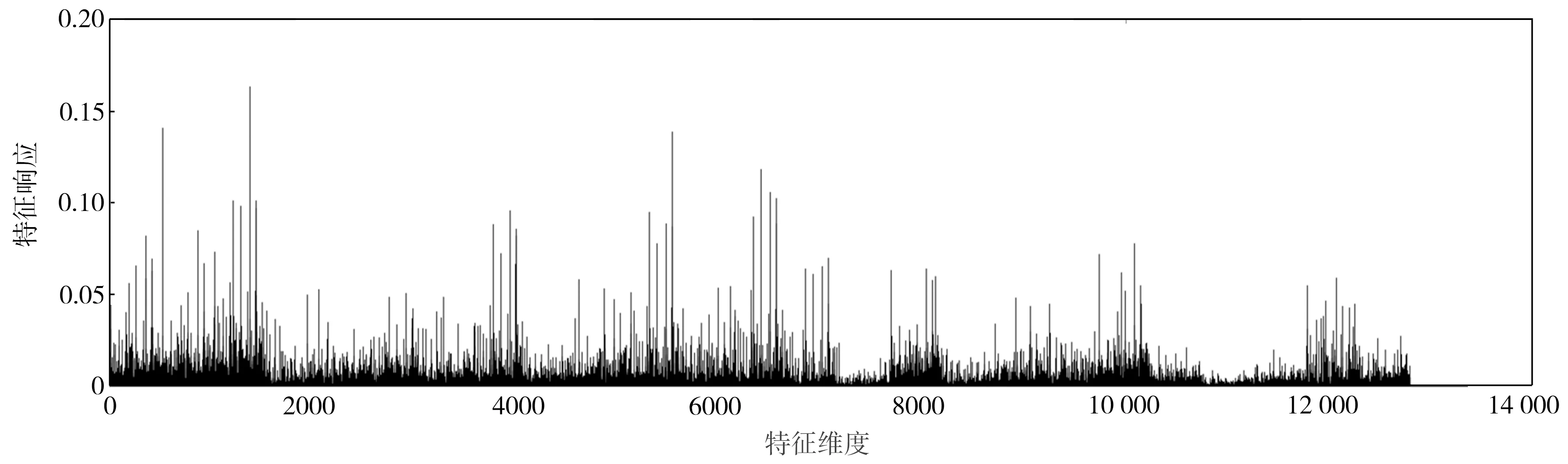
(e)参考图像1的PWA特征响应
(f)参考图像2的PWA特征响应
2 利用幂归一化改进的PWA方法
幂变换可用在很多需要拉伸数据对比度的场合。在数字图像处理领域,幂变换是图像增强算法中经常用到的基本概念,它是一种非线性点运算,选择合适的变换参数可实现图像较亮或较暗区域的对比度增强。针对上述PWA深度聚合特征中的视觉突发现象,本文也采用合适的幂变换函数进行归一化处理,改进特征加权聚合方法,以提高图像检索的精度。
实际上,在原PWA方法中,对部位检测器产生空间权重时,对于选择的通道采用了如式(4)所示的归一化和尺度拉伸的幂变换处理,在一定程度上也是为了减轻不同通道聚合响应之间的巨大差异,但它不能保证最终聚合而成的图像全局特征响应中不再出现突发现象,而图像全局特征表示才是进行图像相似性度量的关键;另一方面,式(4)中有两个幂变换参数即a和b,为了使最终的图像检索结果最优,这两个参数的组合情况很复杂且很难确定。
因此,在本文提出的基于幂归一化改进的PWA方法(power-normalized PWA,PPWA)中,为了达到在最终形成的全局特征基础上抑制突发度的目的,同时为了减少不必要的计算量及减小参数选择的难度,先直接使用选定的通道特征图作为空间权重矩阵,即将式(4)改为:
Sn(i,j)=X(n)(i,j)
(9)
再将幂归一化方法用到原PWA聚合后的特征中,直接对式(6)中每个特征维进行参数为θ(0<θ<1)的幂变换:
p(z)=sgn(z)|z|θ
(10)
式中:p(·)为幂变换函数;sgn(·)为符号函数;|·|表示求绝对值;z为任一特征维上的取值。
记幂归一化后的区域聚合特征为:
Fnθ=p(Fn)=[p(fn,1),p(fn,2),…,p(fn,K)]
(11)
则图像全局特征变为:
Fppwa=[F1θ,F2θ,…,FNθ]
(12)
后处理步骤中只需要进行PCA降维及白化操作,就得到最终更紧凑的D维全局特征表示,即式(8)相应地变为:
Ffinal_ppwa=diag(σ1,σ2,…,σD)-1PFppwa
(13)
选取合适的参数θ,将最终的全局特征用于图像相似性度量,可以比原PWA方法取得更好的图像检索效果。相比于式(4)要选取两个变换参数,这里只需要选取1个,这也便于通过实验进行确定。
PPWA方法的作用效果可以由图2来说明。图2(a)和图2(b)分别显示了将图1(a)作为查询图像、使用PWA和PPWA在Oxford5k数据库上进行检索后返回的Top-16结果 (即前16幅最相似图像,按相似性大小从左到右、从上到下排列)。在PWA方法的检索结果(图2(a))中,图1(b)排在了第10位,而图1(c)却不在这前16幅图像中;在PPWA方法的检索结果(图2(b))中,图1(c)排在了第10位,而图1(b)已经排除在这前16幅图像之外了,这也是图像检索希望看到的结果。同时也不难发现,从所有检索出的图像来看,PPWA方法优于PWA方法。

(a)PWA方法 (b)PPWA方法
图2 采用PWA和PPWA方法对图1(a)中查询图像的Top-16检索结果
Fig.2 Top-16 retrieval results of query image in Fig.1(a) by PWA and PPWA methods
进一步地,如图3所示,从上到下依次显示了图1中3幅图像最终采用PPWA方法聚合后的特征响应。可见,经过幂归一化后的图像响应分布相比改进前较为均衡,特别大的响应得以抑制,降低了其对于相似性度量的影响,而原来较小的一些响应被拉伸,其对比度和区分性得以提升,在相似性度量中的作用也会随之提高,这也是在图2(b)所示的检索结果中图1(c)排在了第10位而图1(b)被排除在Top-16之外的原因。
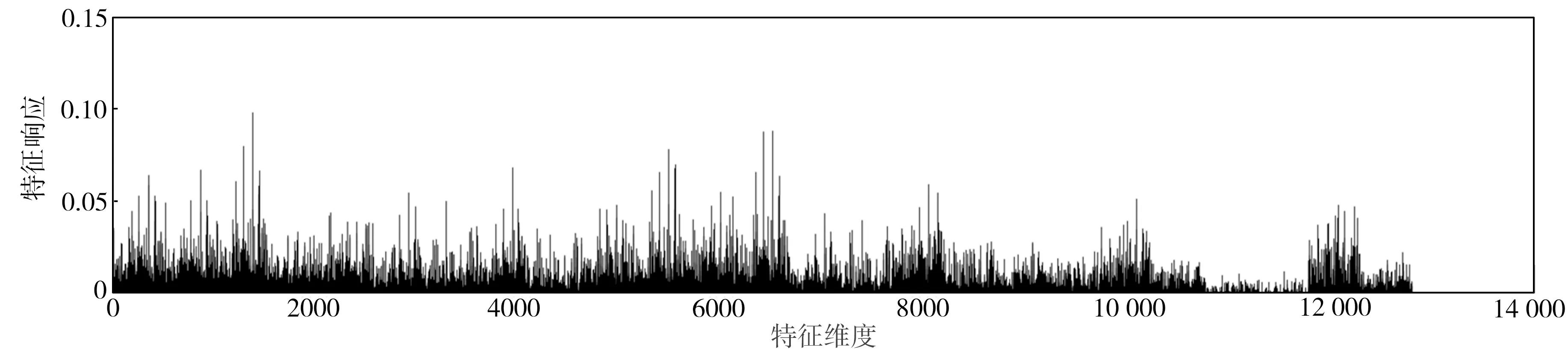
(a)查询图像的PPWA特征响应
(b)参考图像1的PPWA特征响应
(c)参考图像2的PPWA特征响应
3 实验与结果分析
3.1 图像数据库及实验设置
为了进一步验证本文方法的有效性,在公共图像数据库上开展了图像检索实验。Oxford5k数据库[25]包含11个牛津大学标志性建筑物的5062幅图像,Paris6k数据库[26]包含11个巴黎建筑物的6412幅图像,这些图像的拍摄视角和光照条件各不相同,除了需要检索的目标建筑物图像,还包含大量内容各异的其它相关图像。这两个数据库都有55幅查询图像,每个建筑物各有5幅,对要查询的感兴趣区域都进行了标注。每个数据库图像均被分配了“Good”(目标清晰)、“OK”(目标25%以上可见)、“Junk”(目标25%以下可见或目标被严重遮挡或变形)或“Bad”(目标不存在)4个标签之一。评价检索结果时,将标记为“OK”和“Good”的作为正确结果,标记为“Bad”的作为错误结果,标记为“Junk”的则忽略(不影响评价结果)。另外,为了测试检索算法在大规模数据库中的性能,还用含有99 782幅图像的Flickr100k数据库[25]进行扩充,分别组成Oxford105k数据库和Paris106k数据库。
实验中采用裁剪出的感兴趣区域作为查询图像,使用欧氏距离计算每幅图像的相似性得分,并按照从高到低的顺序排列,最后采用平均查准率的均值(mean average precision, mAP)评价性能。卷积层特征是用Caffe包[27]从预训练好的VGG16[28]深度神经网络上获取的,提取的是池化层第5层的特征图,特征图总数即通道数K=512。PWA方法中空间权重的变换参数取a=2和b=2(为方便比较,使用了文献[22]中的默认值)。当对Oxford5k进行测试时,使用在Paris6k上学习的PCA降维方式,反之亦然。PCA降维维数分别设置为4096、2048、1024、512、256、128。实验中也比较了使用查询拓展(query expansion, QE)策略进行图像检索的结果,利用前10个搜索出的图像进行查询拓展[29],表示为QE_10。
3.2 参数选择
3.2.1 部位检测器个数
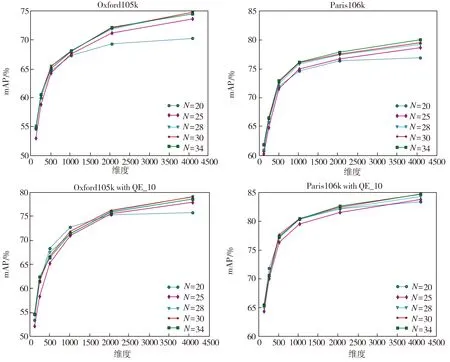
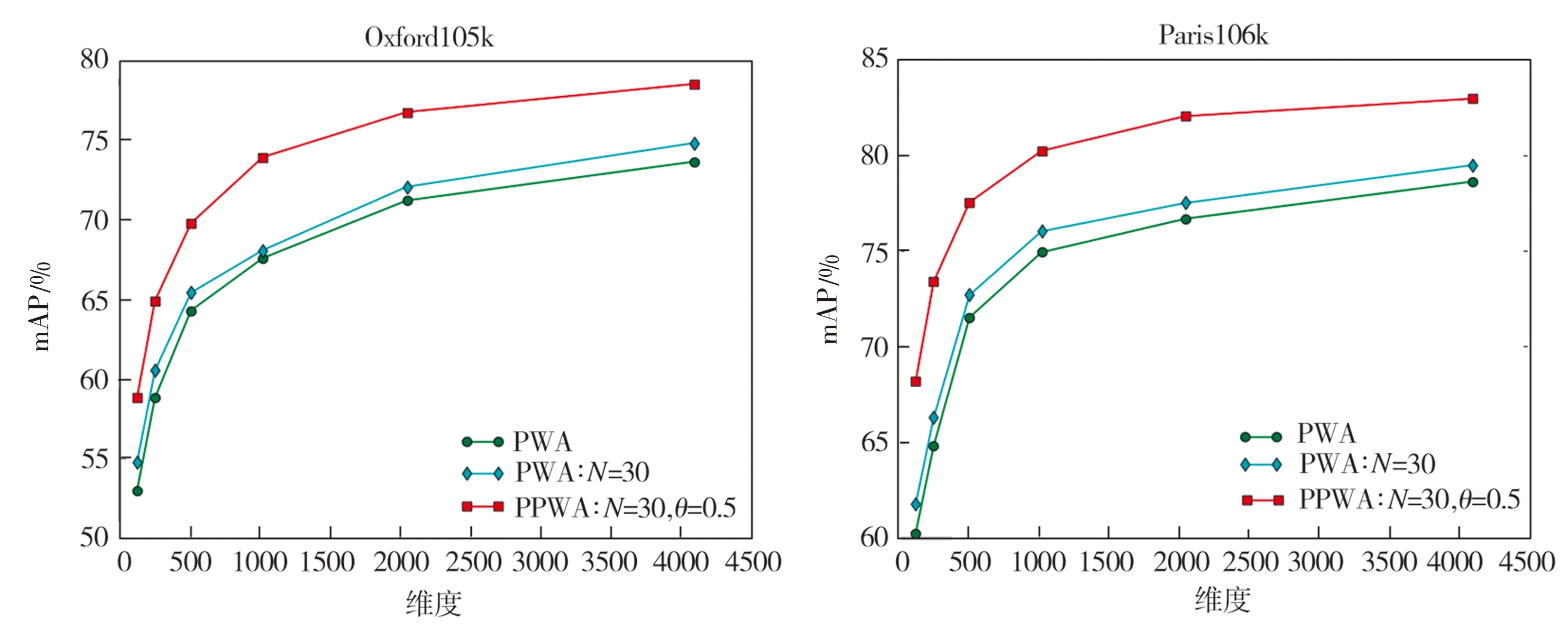
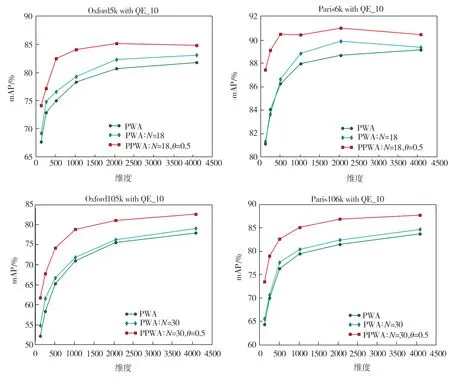
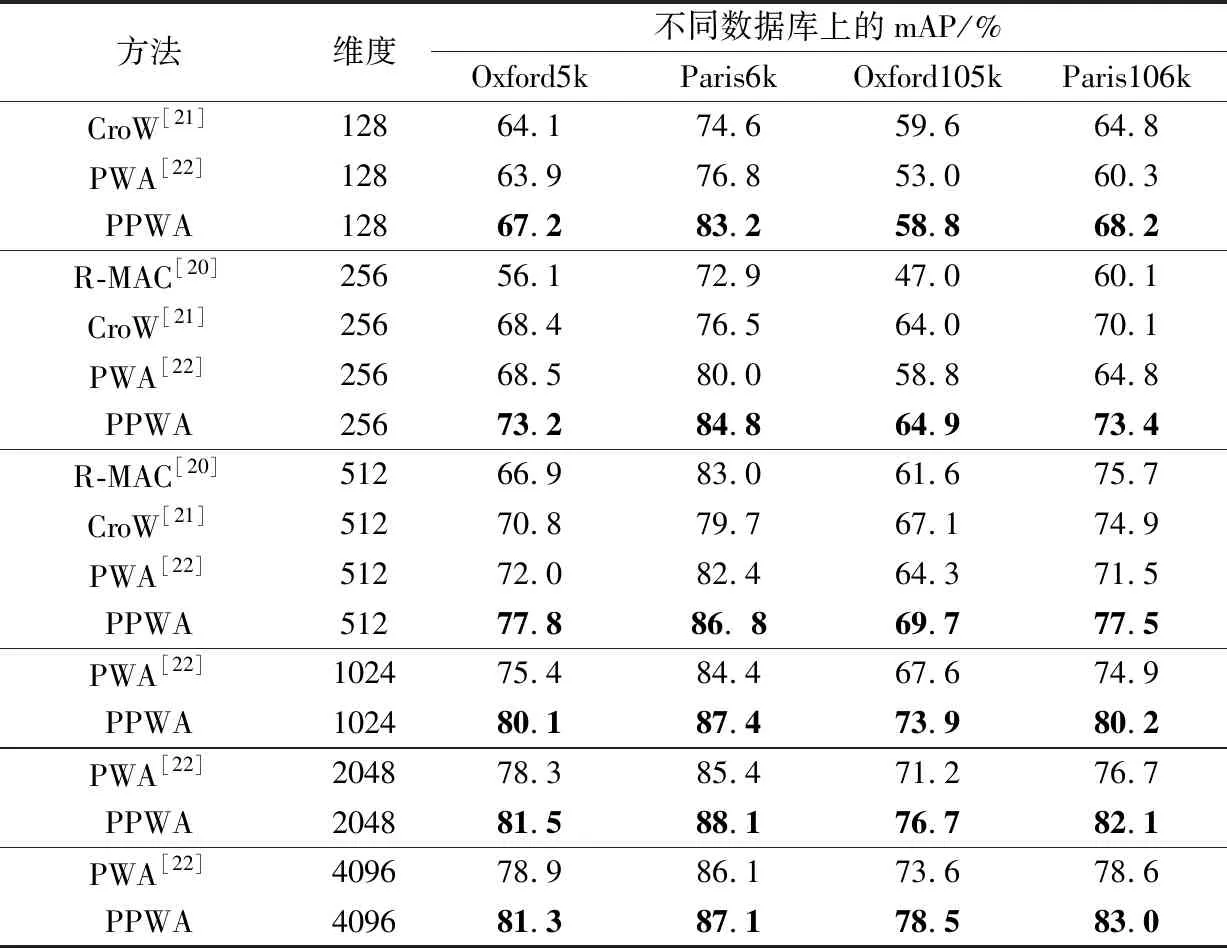
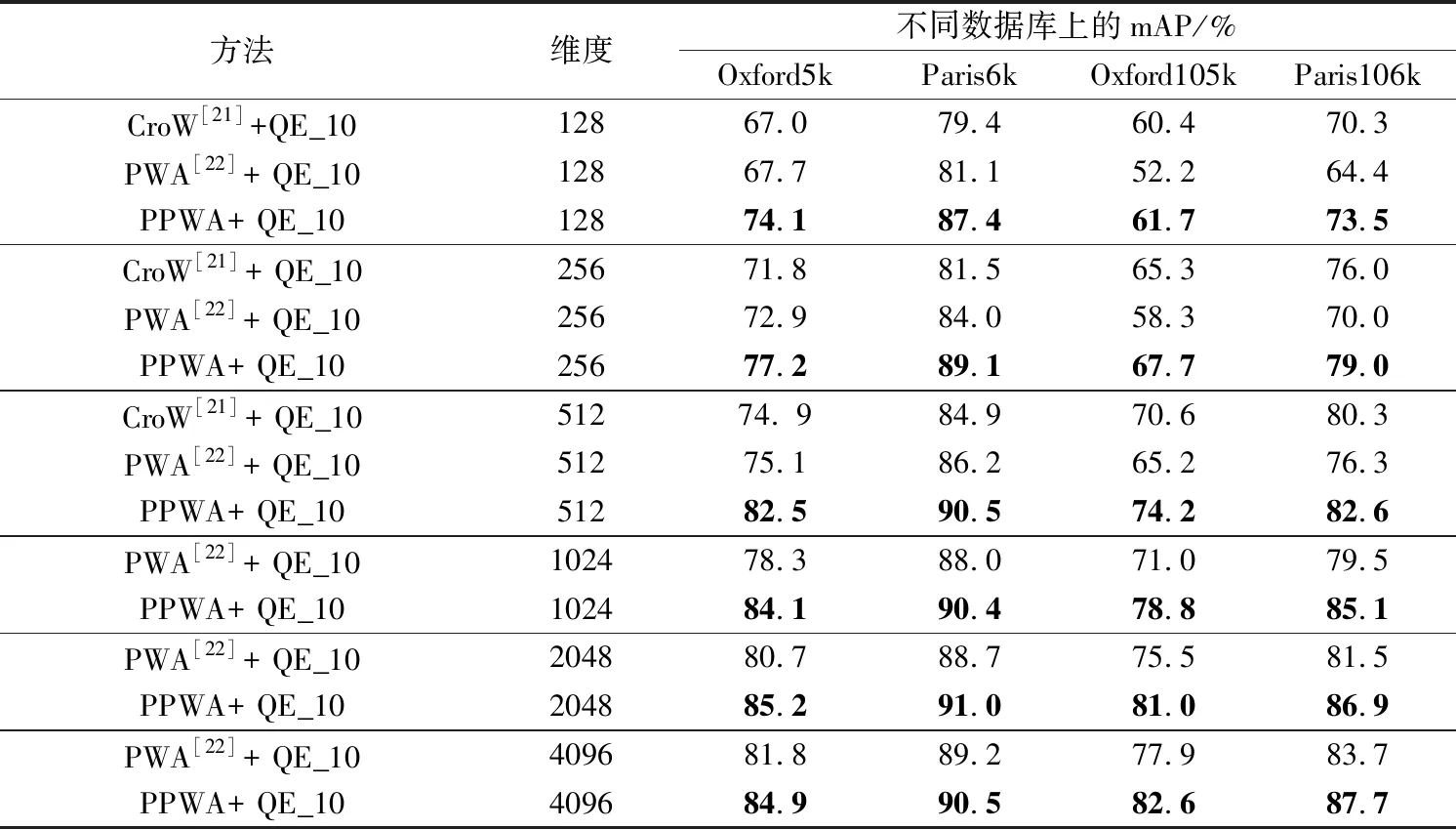
PWA方法中的一个重要参数是所要选取的部位检测器数量,即通道数N(N (a)Oxford5k和Paris6k上的结果(QE表示拓展查询) (b)Oxford105k和Paris106k上的结果(QE表示拓展查询) 从图4中可以看出,在两个规模较小的数据库Oxford5k和Paris6k上,选择较小值N=18时结果最好,而在两个规模较大的数据库Oxford105k和 Paris106k上,选择较大值N=30要比N=25时结果好很多,因此最后确定在Oxford5k和Paris6k上使用N=18,在Oxford105k和Paris106k上使用N=30。 3.2.2 幂归一化参数 对本文提出的PPWA方法中的参数θ在两个小数据库上进行了测试,结果如图5所示。由图5可见,在参数θ=0.5时能获得相对较好的结果,因此后续实验选择θ=0.5作为PPWA方法的幂归一化参数。 根据所选择的参数,在上述4个数据库上进行图像检索实验,对比分析原PWA方法和本文改进后的PPWA方法,实验结果如图6所示。从图6中可以看出,在两个规模较小的数据库Oxford5k和Paris6k上,与原PWA方法(N=25)相比,选择更适合的部位检测器个数(N=18)可以获得更高的精度,同时,使用本文改进方法即PPWA又进一步提高了检索精度。对于两个规模较大的数据库也有相同的实验结果。 将本文方法与其它几个深度特征聚合方法的性能对比结果列于表1和表2中,可以看出,采用本文方法的图像检索平均正确率均高于对比方法,验证了PPWA方法的有效性。 从表1和表2中也可以看到,在不同维度和不同数据库上, PPWA 都要优于原PWA方法。未使用拓展查询策略时(表1),PPWA相比于PWA在两个小数据库上的mAP值提高了1.2%~8.3%, 在两个大数据库上的mAP值提高了5.6%~13.3%;在使用拓展查询策略QE_10时(表2),PPWA相比于PWA在两个小数据库上的mAP值提高了1.5% ~ 9.9%,在两个大数据库上的mAP值提高了4.8% ~ 18.2%,这也表明PPWA方法返回的前10个图像与查询图像更相似,这正是图像检索希望看到的结果。特别地,在低维度(比如128和256维)时,PPWA方法在小规模数据库上获得的mAP值相对于PWA方法有5%以上的提升,在大规模数据库上的精度提升更达到了10%以上,这验证了PPWA方法在低维特征情形下的鲁棒性,也表明其更适用于在大规模图像检索中为了提高效率而选用低维特征的情况。 (a)未使用拓展查询时在4个数据库上的性能表现 (b)使用拓展查询时在4个数据库上的性能表现 表1 PPWA与其它方法的检索性能对比 Table 1 Comparison of retrieval performance between PPWA and other methods 方法维度不同数据库上的mAP/%Oxford5kParis6kOxford105kParis106kCroW[21]12864.174.659.664.8PWA[22]12863.976.853.060.3PPWA12867.283.258.868.2R-MAC[20]25656.172.947.060.1CroW[21]25668.476.564.070.1PWA[22]25668.580.058.864.8PPWA25673.284.864.973.4R-MAC[20]51266.983.061.675.7CroW[21]51270.879.767.174.9PWA[22]51272.082.464.371.5PPWA51277.886. 869.777.5PWA[22]102475.484.467.674.9PPWA102480.187.473.980.2PWA[22]204878.385.471.276.7PPWA204881.588.176.782.1PWA[22]409678.986.173.678.6PPWA409681.387.178.583.0 表2 加入拓展查询(QE_10)后PPWA与其它方法的检索性能对比 本文采用幂归一化方法来调节深度特征聚合中的视觉突发现象,对典型的深度卷积特征聚合方法PWA进行了改进。幂归一化可以抑制少数通道的巨大响应,提高多数较小的通道响应在相似性度量中的重要程度。去除冗余的空间权重变换方法以及选取合适的幂归一化参数,使得改进的PWA方法即PPWA在没有增加计算开销的情况下大大改善检索精度。在多个数据库上的图像检索实验中,使用不同的特征维度以及拓展查询策略都证实了本文方法能有效提高基于深度聚合特征的图像检索准确率。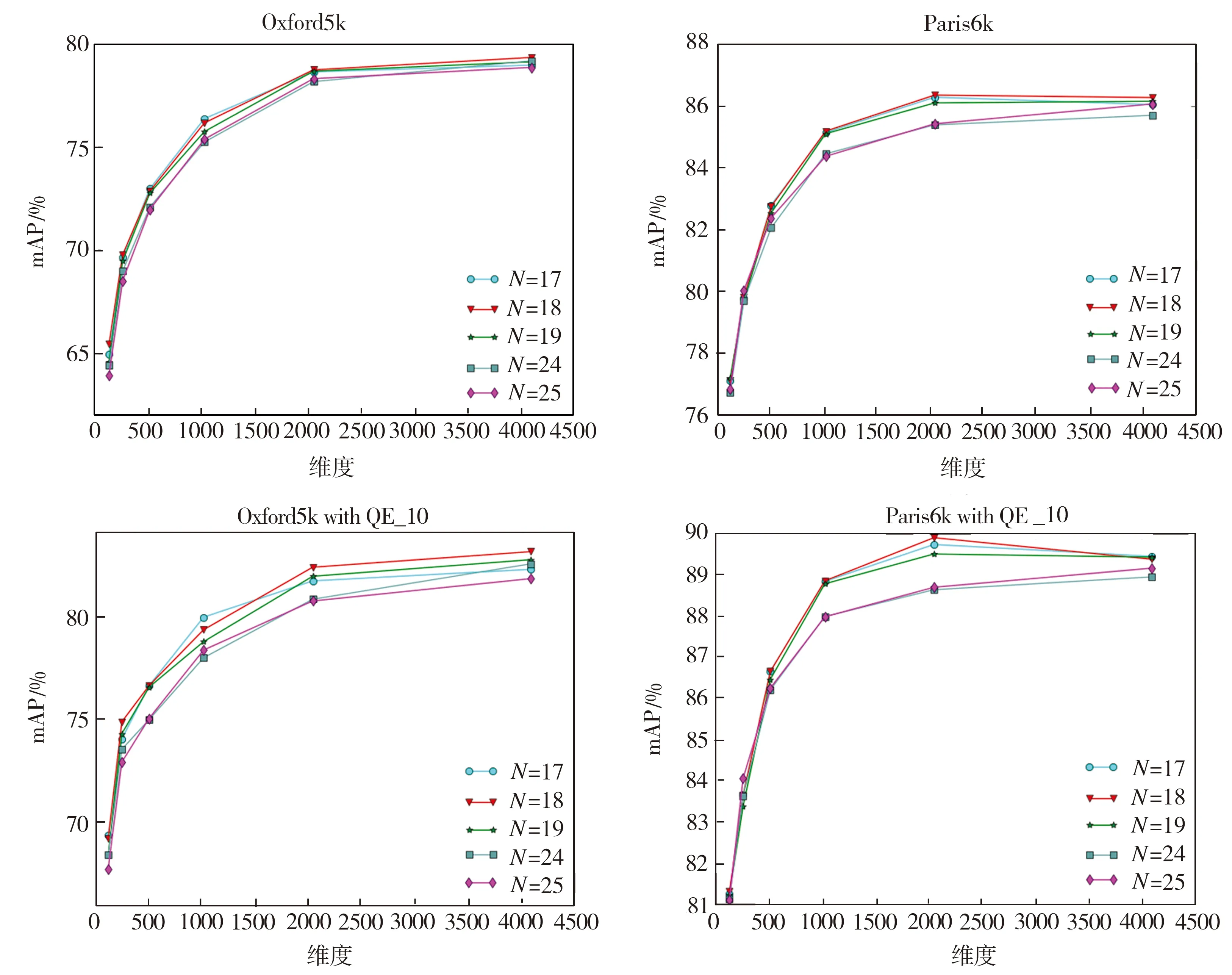
3.3 实验结果分析
4 结 语

