多线圈薄板电磁加热的均匀性及可控性

王宏民 刘燕鑫 许家忠

(哈尔滨理工大学，哈尔滨，150080)

随着电磁感应加热技术的日趋成熟，此技术在工业、商业、生活中都得到广泛的应用，目前，加热物体的热均匀性主要靠自身热传递以及热辐射完成[1]，但当加热板为薄板时，加热板自身的导热性大大降低，导致加热板的热均匀度变差以及加热板温度难以控制。

针对电磁加热温度均匀性与可控性问题，孙彬彬等[2]提出了双线圈平板加热装置，并从电流和频率方面研究温度的提升速度；余露等[3]从电流密度载荷以及频率影响因素对平板硫化机热板表面温度场的均匀性进行了分析，结果表明，电流密度以及频率对硫化机加热板的均匀性有不同的影响；张思彦等[4]提出了一种七线圈结构电磁炉加热装置，通过与单一线圈作对比使单一线圈存在的温度死区现象得到改善。以上均从不同角度对加热板的受热均匀性以及温度提升问题做了不同的分析，但目前，很少有对5 mm以下的加热薄板热均匀性与可控性问题做深入研究。本文主要针对薄板建立矩阵式多线圈电磁加热模型，通过对参数优化构建电磁加热模型，并将构建的矩阵式多线圈加热模型导入ANSYS软件中的Workbench模块进行温度场瞬态求解，分析流过矩阵式多线圈中的电流强度与相邻线圈间距离对薄板温度均匀性影响、气隙长度与频率对温度的可控性影响。

1 数学模型的构建

1.1 电磁场有限元计算数学建模

电磁场宏观规律的描述，主要是对麦克斯韦方程组进行研究，

(1)

式中：E、B、H、D、J、ρ，均为位置r与时间t的时变函数；E(r，t)为电场强度；D(r，t)为电位移；H(r，t)为磁场强度；B(r，t)为磁通量密度；J(r，t)为传导电流密度；ρ(r，t)为电荷密度；为梯度算子。引入矢量磁势(A)和标量电势(φ)与电势得定义[5]：

(2)

将式(2)中的B和J带入式(1)得磁势方程：

(1/μ)(×A)=-σ(∂A/∂t)+J0。

(3)

式中：J0为线圈电流密度。以上3个方程式在空间中任何一点都成立。

1.2 涡流场以及温度场有限元计算数学模型

对于涡流场，可以退出以矢量A为变量的表达式[6]：

(1/μrμ0)××A=Js-σ(∂A/∂t)。

(4)

式中：μr为相对磁导率；μ0为真空中磁导率；σ为电导率；Js为激磁电流。对方程式(4)进行求解，得感应涡流：

J=-σ(∂A/∂t)=-jω。

(5)

感应加热中，涡流所产生的焦耳热作为热源(Qe)，表达式为：

Qe=|J|2/σ。

(6)

对于热传导场，应用傅里叶热传导方程计算温度场，其表达式为：

λ2T-cρ(∂T/∂t)=-Qe。

(7)

式中：λ为导热系数；c为比热容；ρ为物体的密度；T为温度。薄板表面因对流引起的热量损耗由傅里叶边界条件确定，其表达式为：

-λ(∂T/∂n)=h-(Ts-Ta)。

(8)

式中：h为对流热换系数；Ts为变表面温度；Ta为环境温度。联立式(4)～(8)得出薄板表面任意时刻温度分布。由于磁热耦合的实际计算过程十分复杂性，其中，电磁线圈的尺寸、结构、薄板的厚度、材料属性等影响因子，在很大程度上影响着薄板表面涡流和温度分布[7]；多线圈结构中，相邻线圈间的邻近效应使感应出的磁场因流过线圈电流相位的不同而相互叠加或相消[8]；磁-热耦合的非线性问题属于三维范畴，因此，我们无法对其进行理论计算；针对以上问题，本文采用有限元法实现矩阵式多线圈结构中涡流场与温度场的双向耦合。耦合场求解流程如图1所示。

图1 耦合场求解流程图

2 仿真模型的构建

2.1 矩阵式多线圈结构电磁加热模型构建

仿真模型的合理构建有助于提高薄板温度数值模拟的准确性。本文仿真加热系统模型，由加热薄板、外部空气场、线圈构成，加热薄板为铁质材料，密度7 874 kg/m3，线圈在三维坐标系中呈矩阵式排列，根据相关参数(见表1)，构建多线圈加热系统仿真模型(见图2)。当线圈中通入频率为f的激励信号i(t)时，线圈周围将产生交变磁场，磁感线穿过薄板形成闭合磁路[9]；根据电磁场理论，处于变化磁场中的薄板内将产生感应涡流，以感应涡流损耗作为内热源[10]，进而对薄板进行加热。薄板涡流分布及流向，薄板的网格划分如图3所示。

表1 仿真模型相关参数

图2 薄板电磁加热系统仿真模型

由于铁质材料的电导率、磁导率、导热系数、比热容，会随着薄板温度的升高而呈非线性变化，因此他们会对加热薄板温度分布有很大的影响[11-12]，加热薄板材料物理参数与温度的关系如表2所示。

2.2 两种结构的仿真模拟比较

保证其他条件以及相邻线圈中心距相同的情况下，分别对矩阵式结构以及蜂窝状结构进行仿真模拟分析，并比较以被加热薄板几何中心为基点，温度沿径向呈递减梯度变化量以及同等温度区间下的有效加热面积。模型几何参数如表1所示：相邻线圈间相位互差180 ℃、相邻线圈间的中心距为35 mm、单个线圈匝数为100、加载电流为6 A、加热时间为30 s，在涡流损耗以及频率相同的他情况下，得矩阵式结构以及蜂窝式结构薄板温度分布(见图4)。

表2 薄板材料(铁)物理参数

图3 薄板涡流分布及流向和薄板的网格划分

图4 薄板温度分布

由图4可见：以被加热薄板几何中心为基点，温度沿径向呈递减特征；在有效加热区域内，矩阵结构与蜂窝结构温差变化量分别为4.46、8.39 ℃，有效加热面积分别为6 120.68、4 280.45 mm2。以上表明，在同等边界条件下，矩阵式多线圈结构的递减率比蜂窝结构的小53.16%；以及同等温度梯度下，矩阵式多线圈结构的有效加热面积，比蜂窝结构有效加热面积大43.52%。因此，采用矩阵式多线圈结构在薄板温度的均匀性以及加热效能上，优于蜂窝结构。

3 加热薄板涡流场及温场仿真模拟

3.1 电流强度对薄板表面温差的影响

以矩阵式线圈结构构建模型，在气隙长度、加热时间、电流频率、薄板厚度等一定的情况下，分别计算不同电流强度作用下，薄板表面有效区域温度分布情况。设置加热时间为30 s，加热频率为40 kHz，线圈匝数为100匝，分别对电流强为3、4、5、6、7、8、9、10 A时的薄板表面温度进行仿真模拟(见图5)，分析薄板有效区域表面温差随电流强度的变化趋势(见表3)。

表3 随着电流强度的增大薄板表面径向温差与有效区域面积

电流强度/A有效区域温差/℃有效区域面积/mm21021.104371.82913.285538.96810.975695.7678.415766.3865.985851.8154.326025.3942.755792.9731.505632.05

由图5、表3可见：在电流强度从3 A至10 A的变化过程中，薄板沿径向温度梯度有效区域表面温差，从1.50 ℃增大到21.10 ℃，变化量为19.60 ℃，温差呈上升趋势，有效加热区域面积先增大后减小。由此可以得出：在其他条件特定的情况下，薄板表面径向有效区域的温差与电流强度呈正相关，且温差增大的幅度呈增大趋势；因此，电磁加热设计时，在一定的条件下，选择较小电流强度才能使加热效果更均匀。

图5 薄板表面温度分布云图

3.2 相邻线圈间的间距对薄板表面温差的影响

在一定的范围内，对相邻线圈间的间距进行适当的调整，并进行仿真模拟，通过薄板温度分布云图分析薄板表面径向有效区域温度分布情况。设置相邻线圈间的中心距为35 mm、加热频率为40 kHz、加热时间为30 s、线圈的电流强度为5 A，相邻线圈间的距离分别为1、5、9、13、17、21 mm，仿真模拟显示，薄板表面沿径向有效区域温差分别为7.42、5.87、4.80、3.43、2.35、0.60 ℃。仿真模拟结果表明：在确保中心距为35 mm的情况下，在一定范围内，适当的调整线圈间距离，距离从1 mm至21 mm的变化过程中，薄板表面径向有效区域温差从7.42 ℃减小到0.60 ℃，变化量为6.82 ℃，呈下降趋势；加热薄板有效区域面积增加8.92%。由此可以得出：在电流密度、频率、线圈间中心距特定情况下，在间距一定范围内，适当调整相邻线圈的间距，薄板表面径向温度梯度有减小特征；与此同时，薄板表面有效区域加热温度也随之减小。因此，在设计电磁薄板加热时，在一定的范围内，确保加热温度的基础上，选择较大的线圈间距才能使薄板表面温度更均匀。

3.3 气隙长度以及频率对薄板表面温度的影响

在电流密度、加热时间、电流频率、线圈中心距、线圈间距等一定的情况下，采用矩阵式结构加热，在保证薄板温度均匀的前提下，分别对厚度为0.9、1.2、1.5 mm的薄板在不同气隙长度下进行数值模拟，并分析薄板表面有效区域温度的可控性。设置加热频率为40 kHz、加热时间为30 s、气隙长度为1～21 mm之间时，模拟不同薄板厚度以及气隙长度所对应的薄板表面温度(见图6)。

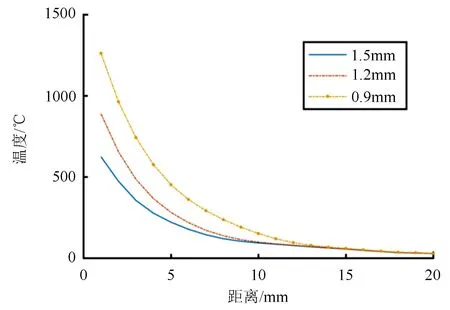
图6 不同薄板厚度以及不同气隙长度时的薄板表面温度

同时在气隙长度为6 mm、加热时间为30 s、薄板厚度为0.9 mm、电流强度为6 A等一定的情况下，分别计算不同电流频率作用下，薄板表面有效区域温度；线圈匝数为100匝，电流频率分别为10、20、30、40、50 kHz时薄板表面温度(见图7)。

由图6、7可见：一定范围内，在薄板表面温度均匀的基础上，当薄板厚度分别为0.9、1.2、1.5 mm时，气隙长度由1 mm至20 mm变化的过程中与薄板表面温度呈负相关；薄板表面温度与频率呈正相关。因此，在电磁加热设计时，一定的条件下，根据所需温度要求，通过调整气隙长度以及频率进而达到对薄板加热温度进行控制。

图7 薄板表面温度随频率变化曲线

4 结论

针对薄板电磁加热温度均匀性及可控性问题，本文提出新型矩阵式多线圈加热结构，为问题的解决提供了有效途径。在涡流损耗与模型尺寸相同的条件下，通过建立矩阵式线圈结构与蜂窝式线圈结构进行薄板表面温度均匀性仿真模拟比较，并分析流过矩阵式多线圈结构中的电流强度和线圈间距离对薄板温度均匀性影响以及通过实验得知气隙尺寸和频率对温度的控性关系。

多线圈结构下，薄板温场以几何中心点沿径向呈温度递减分布，在同等边界条件下矩阵结构的递减率比蜂窝结构小50%以上，而相同温度梯度对应的有效加热面积大40%以上。因此，矩形线圈结构在薄板温度的均匀性以及加热效能上优于蜂窝结构。

采用矩阵式多线圈结构进行加热，电流密度以及频率一定的情况下，薄板表面的径向温度梯度与电流呈正相关；适当调整相邻线圈的间距，薄板表面有效加热区域面积与间距呈正相关，薄板表面温度的均匀性得到改善。

仿真结果表明，矩阵式多线圈结构中气隙长度与薄板表面温度呈负相关，频率与薄板表面温度呈正相关，因此，通过选择合适气隙长度及调节频率实现薄板表面温度的有效控制。

本文对矩阵式多线圈结构所做研究，可为薄板电磁加热温度均匀性以及可控性设计提供参考。