基于数据挖掘技术的高校教学质量监控研究

郭欣 章鸣嬛 吴良 陈瑛

摘 要： 教学质量监控是学校进行教学质量管理的重要手段，对提高教学质量具有重要意义。随着校园信息化的发展，高校教务系统里积存了大量有价值的数据，但却没有被很好的挖掘利用。鉴此提出将数据挖掘技术应用到高校教学质量监控中，使用因子分析法对计算机专业的学生成绩进行综合评价分析，并提出一种决策树改良方法对学生成绩进行预测，最后针对文中所提出的方法与其他方法进行了对比分析。结果表明，

因子分析法相对于平均分排名法，蕴含了更多的信息量可以提供更加全面的评价，另外其突出重要因素，可以对各方面情况进行合理量化;决策树改良方法相对于其他成绩预测方法稳定性好、准确性高，且过拟合情况少。经验证，这个方法可以在高校教学质量监控中发挥一定作用。

关键词：数据挖掘技术; 教学质量监控; 因子分析; 决策树; 聚类

中图分类号： TP311      文献标志码： A

Research on Teaching Quality Monitoring in Universities

Based on Data Mining Technology

GUO Xin1， ZHANG Minghuan1， WU Liang2，

CHEN Ying1*

Abstract： Monitoring teaching quality is an important means in teaching quality management in schools， and it is of great significance to improve the teaching quality. With the development of campus informatization， a lot of valuable data have been accumulated in the educational administration system of universities， but they have not been well mined and utilized. So this paper puts forward the application of data mining technology to the monitoring of teaching quality in universities. The factor analysis method is used to make a comprehensive evaluation and analysis of the students' achievements in computer major， and a decision tree improvement method is proposed to predict students' achievements. Finally， the methods proposed in this paper are compared with other methods in detail. The results show that factor analysis method contains more information than traditional methods and can provide more comprehensive evaluation. In addition， it highlights important factors and can quantify all aspects of the situation reasonably. Compared with the other methods， the improved method of decision tree has better stability， higher accuracy and less overfitting. It has been proved that the method proposed in this paper can play a certain role

in the monitoring of teaching quality in universities.

Key words： Datamining technology; Teaching quality monitoring; Factor analysis; Decision tree;

Clustering

0 引言

教学质量是高校生存和发展的生命线，学校通过教学质量监控体系发挥教学信息收集、教学效果评估、教学过程诊断和教学质量提高的作用，对课程成绩进行监控是高校教学质量监控体系的重要内容[1]。近年来高校的校园信息化建设已经日臻成熟，高校教务系统里积存了大量有价值的成绩数据，但却没有被很好的挖掘利用，多数还停留在数据备份、简单查询、采用基础的统计方法进行分析以及使用简单的图表进行展示等方式上[2]。数据挖掘技术可以进行数据分类和预测、聚类分析和关联分析等，能够对数据进行深层次挖掘，是提高分析和决策能力的重要研究领域[3]。将数据挖掘技术引入教学质量监控，对现有的成绩数据进行客观的分析，并挖掘出有价值的信息，无疑将有助于改进教学措施，提高教学质量[4]。

目前，已有将数据挖掘技術应用于教学管理的相关研究，如文献[5]研究了基于频繁模式谱聚类的课程关联分类模型和学生成绩预测算法;文献[6]提出一种基于K近邻局部最优重建的残缺数据插补方法并结合随机森林模型实现了成绩预测;文献[7]研究如何借助多种预测和统计手段用本科成绩数据推测学生在研究生期间的表现。本文在借鉴前人研究经验的基础上，使用因子分析法对计算机专业的学生成绩进行综合评价分析，并提出一种决策树改良方法对学生成绩进行预测，最后针对文中所提出的方法与其他方法进行了详细的对比分析，从中找到更能促进教学质量监控的方法。

1 数据采集与预处理

本文涉及的所有样本数据均来自我校教务系统，以2018届186名计算机科学与技术专业学生的17门课程的期末考试成绩作为研究对象。为了规范研究数据的归属权与保护数据所有者的隐私，后续涉及相关数据时将采用编号等方式进行虚拟化处理。

由于所研究的数据对象是学生多门课程的期末考试成绩，所以首先需要将数据进行集成，本文利用数据库技术，根据学生学号的唯一性，将不同课程的成绩合并到一个表中。其次，由于缺考或者没有选课等原因，出现某些课程的成绩为空值;另外有部分学生重修某些课程，出现成绩重复的现象，所以接下来需要对集成好的数据进行清洗，方法如下：

（1）对于多门课程没有考试成绩的学生数据直接刪除记录;

（2）对于同一门课程出现多个考试成绩的学生数据采取其第一次考试的成绩记录;

（3）针对部分成绩空缺的学生数据用该课程的平均成绩进行填补;

（4）如果某门课程有多数学生成绩空缺，则认为该课程数据异常，将其进行删除处理。

对数据清洗完成后，为了解决量纲不一致等问题对数据进行Z标准化处理。

2 基于因子分析法的学生成绩综合评价

本文以教育部计算机科学与技术教学指导委员会（下文简称“教指委”）提出的计算机专业人才培养的4项基本能力要求为参考依据（见表2）[8]，选取17门专业必修课成绩为研究对象，根据因子分析的基本原理和步骤，对学生成绩进行综合评价。这17门课分别为：计算机组成原理（X1）、计算机电路基础（X2）、数据结构（X3）、计算机网络（X4）、离散数学（X5）、微型机接口技术（X6）、操作系统（X7）、C++面向对象程序设计（X8）、数据库原理与技术（X9）、算法设计与分析（X10）、JSP/ASP

WEB技术（X11）、JAVA语言程序设计（X12）、硬件课程设计（X13）、计算机信息安全（X14）、软件工程（X15）、程序设计语言课程设计（X16）、C程序设计基础（X17）。

2.1 KMO和巴特利特球度检验

KMO和巴特利特球度检验的取样适切性量数为0.957，根据统计学家Kaiser给出的标准[9]，可以认为数据对象适合因子分析。

2.2 提取公因子

由因子分析的共同度可知其提取值都介于0.5到0.8之间，可以认为因子基本能解释各门专业课的方差。另外，从总方差的解释情况可看出旋转后第一个因子的方差贡献率为43.347%，三个因子的累积方差贡献率为69.916%，即三个因子解释了原有17个变量的69.916%含义。

2.3 公因子解释

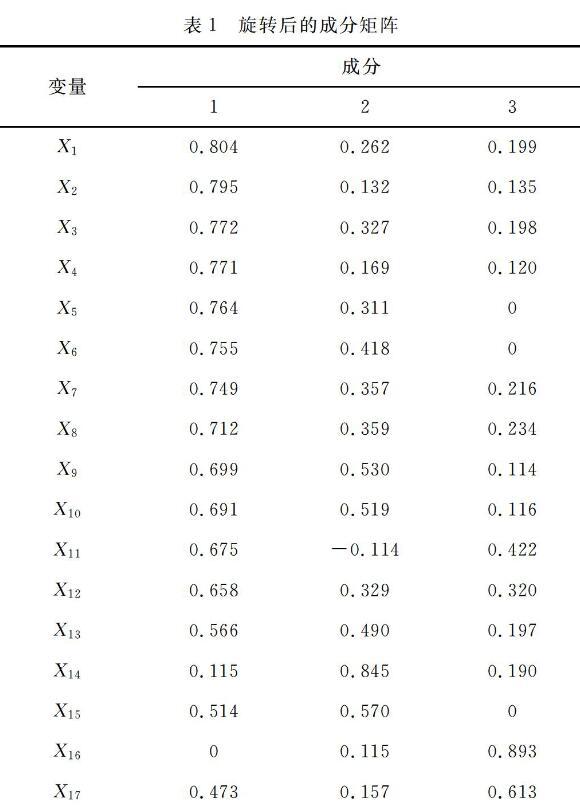
为了使因子变量更具有可解释性，对因子载荷矩阵进行了最大正交旋转，得到旋转后的因子载荷矩阵，如表1所示。

另外，根据教指委的指导意见，我们可以把计算机科学与技术专业本科生的专业能力、知识体系和上述17门课程之间的关系归纳如表2所示。

结合表1和表2可以对3个公因子进行解释：3个因子基本代表了专业能力培养目标所要求的4种能力，其中F1代表综合能力、计算思维能力，F2代表算法设计与分析能力、系统的认知、分析、开发与应用能力，F3代表程序设计与实现能力，如表3所示。

2.4 用公因子进行综合评价

根据回归算法计算出因子得分矩阵，据此可以得到因子得分函数，鉴于篇幅原因，这里只给出F1因子的得分函数，F2和F3雷同如式（1）。

F1=0.154X1+0.213X2+0.117X3+0.194X4+0.149X5+0.112X6+0.093X7+0.076X8+0.029X9+0.03X10+0.205X11+0.05X12-0.021X13-0.322X14-0.015X15-0.216X16-0.012X17

（1）

学生的综合表现由公因子反映，可以用公因子计算每个

学生的成绩综合评分，公因子的权重取其方差贡献率，则综合评分的计算式为式（2）。F=0.574F1+0.072F2+0.054F3

（2）  计算得到综合评分之后，可以将其作为对学生成绩进行排序和比较分析的依据。

3 基于决策树改良方法的学生成绩预测

3.1 决策树改良方法介绍

决策树属于有监督式的机器学习方法 [10]，本文使用的决策树算法是C5.0。C5.0算法对数值变量进行离散化处理时使用的是MDLP（Minimal Description Length

Principle，即最短描述长度原则）的熵分箱方法，其核心测度指标是信息熵和信息增益[11]。该方法不能按照各门课程考试的难易程度和分箱个数自定义分箱规则，不够灵活，因此本文对其进行改良，先使用Kmeans聚类算法对各门课程的成绩数据分别进行离散化处理，再进行目标课程成绩预测。

3.2 确定预测目标

本文的预测目标是通过将教学计划中的专业基础课、专业核心课按照开课的先后顺序进行整理，然后选出较早开设的课程成绩作为解释变量，来预测后续与之相关的高阶专业课的学习成绩，找出有可能挂科的学生，提前对其进行干预，从而达到预警的目的。例如，将“计算机信息安全”作為预测目标，综合考虑开课学期的顺序和课程类别，将C程序设计基础、操作系统、离散数学等9门课的成绩作为解释变量，对目标课程成绩进行预测。

3.3 利用聚类算法进行数据转换

按照前文所述，在使用C5.0算法对目标课程的成绩进行预测之前，要将数据进行转换，即采用Kmeans聚类算法对课程成绩进行离散化处理。表4显示的是聚类分析后各等级的聚类中心点情况，如表4所示。部分学生10门课程成绩经Kmeans聚类算法处理后的样本分布情况，如表5所示。

3.4 利用C5.0算法进行预测分析

将离散化处理后的数据载入SPSS

Modeler，并调用C5.0算法对其进行建模，采用十折交叉验证算法作为模型的评估手段，Boosting算法作为提高预测准确度的方法，以获得最佳的树形结构，最终结果如图1所示。

如图1所示，

“数据库原理及技术”是模型的根节点，可见其是信息熵增益最强的属性，其次是离散数学，再次是C程序设计基础、数据结构等。因此，在9门作为解释变量的课程中，“数据库原理及技术”与“离散数学”对于预测目标课程“计算机信息安全”的成绩的贡献度最大，对于想取得优异成绩和预测结果较差的学生应加强对这两门课程的学习。另外，我们可以对决策树进行规则提取，即沿着决策树的根节点到每一个叶节点的路径用IFTHEN语句进行表示。由于按照图1所示的决策树提取的规则较多，下面只列出“计算机信息安全”评级为“差”的规则，如下：

IF（ 数据库原理及技术=“优”or“中”or“良”） AND（ 离散数学=“良”） AND（ 数据结构=“差”） THEN

计算机信息安全=“差”

从规则中我们可以看出，“数据库原理及技术”的成绩不是预测“计算机信息安全”是否为“差”的决定因素（从完整的决策树可以看出其为预测“计算机信息安全”是否为“优”的决定因素），而“离散数学”和“数据结构”学不好，“计算机信息安全”就有可能挂科，因此当“离散数学”、“数据结构”的成绩不理想时，就应该向相关学生进行预警。

4 分析与讨论

4.1 因子分析与传统综合评价方法对比如表6所示。

（1）因子分析法既可以从整体上对学生成绩进行排序，还可以了解每位学生知识掌握情况的细节，知道学生在哪些专业能力方面得到了较好的发展而哪些相对薄弱，例如表6中f14011632、f14011507两名学生F综合得分近似（分别为第1、2名），但是相比之下f14011632的F1因子得分较高，代表其综合能力、计算思维相对较强，而F2、F3因子得分较低，代表其算法设计与分析，系统的认知、分析、开发与应用，程序设计与实现能力较差，学号为f14011507的学生情况恰好相反。由此可见，相对于传统的平均分排名法，因子分析法蕴含了更多的信息量，帮助教师引导学生及时调整学习和发展的方向。

（2）由表6还可以看出因子分析与传统的平均分排名结果不同，例如f14011632因子分析排名第1，但平均分却排名第9;而f14011407因子分析排名第11，平均分排名却达到第2，仔细观察后不难发现f14011407各项成绩比较均匀，而f14011632的F1因子得分非常突出，这与按平均分排名时各门课的权重相同，而因子分析法F1的权重较大的特点相对应。由此可见，按平均分排名的传统方法没有对课程的重要性进行区分，而因子分析法突出重要因素，对各方面情况进行了合理量化。

4.2 决策树改良方法与其他学生成绩预测方法对比

下面通过实验对比三种成绩预测方法的效果，即直接用C5.0算法、经传统方法离散化处理后再用C5.0算法、决策树改良方法，三者的对照结果如表7所示。

其中，传统的数据离散化方法是区间标记法，即指定一个分数区间将其标记为相应等级（实验中将85-100分标记为优、70-84分标记为良、60-69分标记为中、0-59标记为差），从而替换连续的数值。

由表7可以看出，决策树改良方法的估计准确性最高，所生成的决策树深度最小、叶子节点数最少，这表明由其生成的决策树模型与其他两种方法相比更加准确且健壮。另外，交叉验证结果中决策树改良方法的标准差也较小，说明其模型的稳定性较好，预测的波动较小[12]。整体上来说，由于决策树改良方法在对数据离散化处理时建立了合理的分箱规则，对课程本身的考试难度进行了区分，相对其他两种方法，其效果更好。

5 总结

本文利用数据挖掘技术对学校教务系统里的成绩数据进行了深入地挖掘与剖析。首先对教务系统中的数据进行采集和预处理，然后利用因子分析法对学生成绩进行综合评价，之后用Kmeans聚类算法+C5.0算法的决策树改良方法对目标成绩进行预测，最后将上述方法与其他方法进行了对比分析。分析结果表明：因子分析法相对于传统方法，其分析结果更加全面、合理;决策树改良方法相对于其他预测方法，稳定性好、准确性高，并且生成的决策树更加健壮，可以尽量避免过拟合现象。但是，由于目前拥有的数据有限，结果可能会存在一定的局限性，后续将进一步研究。

参考文献

[1] 乔斌.SPSS在计算机课程教学质量评估中的应用[J].河套学院学报，2013（12）：6566.

[2] 纪连恩，高芳，黄凯鸿，等.面向多主体的大学课程成绩相关性可视探索与分析[J].计算机辅助设计与图形学学报，2018，30（1）：4456.

[3] Jiawei Han， Micheline Kamber 著.数据挖掘概念与技术[M]范明，孟小峰，译.北京：机械工业出版社，2007：8695.

[4] 张甜.基于数据挖掘的高校学生成绩关联分析研究[D].北京：北京邮电大学，2017.

[5] 何楚，宋健，卓桐.基于频繁模式谱聚类的课程关联分类模型和学生成绩预测算法研究[J].计算机应用研究，2015，32（10）：29302933

[6] 曹歆雨，曹衛权，李峥，等.面向不确定残缺数据的大学生成绩预测方法[J].现代电子技术，2018（6）：145149.

[7] M Saarela，T K？rkk？inen. Analyzing Student Performance using Sparse Data of Core Bachelor Courses [J]. JEDMJournal of Educational DataMining，2015，75（1）：332.

[8] 教育部高等学校计算机科学与技术教学指导委员会.高等学校计算机科学与技术核心课程教学实施方案[M].北京：清华大学出版社，2009：45.

[9] Jin Hailiang， Liu Huijie. Research on visualization techniques in data mining[C].2009 International Conference on Computational Intelligence and Software Engineering， 2009.CiSE2009.International Conferenceon. IEEE，2010：131133.

[10] 商俊燕，陸兵，柏倩然.决策树C4.5算法在学生成绩分析中的应用[J].微型电脑应用，2015，31（4）：4345.

[11] Kaur P， Singh M， Josan G S. Classification and prediction based data mining algorithms to predict slow learners in education sector[J].Procedia ComputerScience，2015，57：500508.

[12] Ahmed M， Zafar B， Manzoor U. Modeling and predicting students' academic performance using data mining techniques[J].International Journal of Modern Education and Computer Science，2016（8）：36.

（收稿日期： 2019.07.22）

基金项目：2018年教育部高教司协同育人项目（201802001049）;2018年教育部高教司协同育人项目（201802111036）

作者简介：郭欣（1982），女，讲师，硕士，研究方向：数据挖掘与分析。

章鸣嬛（1980），女，副教授，博士，研究方向：计算机应用。

吴良（1955），男，教授，硕士，研究方向：教学质量管理。

通信作者：陈瑛（1968），女，教授，博士，研究方向：数据工程。文章编号：1007757X（2020）01000704