在“说”中“知其行”

鲍澜澜

【摘要】曾经有学者对学习和日常生活中信息交流的情况做过统计：听占45%，说占30%，读占16%，写占9%。这说明，听和说在信息交流中占有比较重要的地位[1]。文章探讨了怎样才能让学生“想说”“会说”，从而使学生在学习知识的同时，语言、思维也得到同步发展，更好地实现核心素养下的培养目标。

【关键词】说;言语表达;思维能力

著名的心理学家邵瑞珍在其编著的《教育心理学》中指出：“由于言语表达具有重要的提炼功能，所以思想经过语言的精确表达之后，就增加了意义和迁移的可能性。”[2]据此，我们应该把言语表达看作整个思维过程的一个组成部分。为此，在课堂教学中，我們要创造条件让学生表达，加强对学生说的训练，在不同课型与各个环节都要加强对学生进行说的训练，培养学生的口头表达能力。下面结合具体教学实践，从计算教学中、概念教学中、解决问题教学规定知识中来谈一谈如何让学生在“说”中“知其行”。

一、计算教学中的“说”

计算题，很多学生会做，但不能规范、有条理地说出来。因此，在计算教学中应重视说的过程，这样既能帮助学生巩固所学的计算方法，加强算理教学，又能发展学生思维。在计算教学中，应让学生说算理、说运算顺序和说计算方法[3]，并且对于计算中出现的错误，要让学生说出错误的原因等，从而有效进行“说”的训练，培养学生的表达能力。

1.说算理

计算教学的重点是弄清算理，掌握计算法则。学生是否理解算理，掌握算法，那就要看他能否清楚完整地说出来。只有学生说出来，教师才能收到反馈信息，了解学生的掌握情况，而说算理也是学生深入理解、掌握知识的过程。

例如：在教学二年级下册“三位数加两位数”时，先出示“85+143=？”让学生独立计算，再引导学生说一说这样算的理由，从而让学生讲清算理。即：由于85是由8个十和5个一组成的，143是由1个百、4个十和3个一组成的，所以先把5个一与3个一相加得8个一;再把8个十与4个十相加得12个十;十位相加满十要向百位进1，十位上写2，向百位进1，百位上原来的1加上十位上进上来的1等于2，结果是228。这样进行说理训练，学生的思维越来越有条理性，同时加深了对算理的理解。

2.说算法

在交流算法的过程中，要训练学生清晰而有条理地说出计算方法，加深对所学知识的理解。例如：在教学三年级下册“两位数乘两位数”时，通过情境图学生知道了这道题要求订一份牛奶要花多少钱，就是用28×12，然后让学生独立进行计算，并引导学生说一说自己是怎样计算的。生a：可以先求出10个月要多少钱？即10个28是多少，再求2个月要多少钱？即2个28是多少，然后把两个积加起来。生b：可以用竖式计算，先用2去乘28得56，再用1个十去乘28得到28个十，因此，应把8写在十位上，2就要写在百位上，然后把两次相乘的积相加。让学生知道在说的过程中，进一步明确计算乘数时两位数的乘法要分三步走，前两步乘，第三步相加，这样让学生在反复说的过程中，能够进一步理解与掌握计算方法。

3.说错因

教学中，教师经常会感慨：这题做过好多次了，为什么还出错呢？其实，有时苦口婆心的说教，不如让学生在纠错中自评自省。例如：在教学四年级下册“运算律”之后，练习九有这样一道练习题：294-36+64。很多学生因为受到加法结合律的思维定式影响，写出294-36+64=294-（36+64）。对此，老师并没有做出任何评判，而是让学生自己发表见解。

生1：我觉得可以简便计算，这种解法是运用了加法结合律。

生2：我认为不可以简便计算，因为加法结合律都是几个数连加，而这里是加减混合运算。

生3：（恍然大悟）对，这道题不能简便，因为是加减混合运算，所以要从左到右依次计算。

师：那怎样才可以这样解答呢？

生1：只有是294-36-64时才可以用294-（36+64）解答，刚才我做错了。

有一位社会心理学家这样说：“我们期望学生犯错误，因为从错误中吸取教训，便可争取明天的成功。”这样让学生说出错误的原因，能让学生更好地理解算理和掌握法则，同时也促进了学生思维的发展。

二、概念教学中的“说”

小学数学概念有其严格的科学性，要遵循辩证唯物主义的认识论及符合儿童的认知规律。在概念教学中进行“说”的训练，是由直观认识转化为理性认识，用既准确又概括的数学语言把各种概念、公式、法则和性质等揭示出来。学生只有形成正确、清晰、完整的数学概念，才能掌握好基础知识。如果学生连概念本质都说不清楚，数学知识就成了“水中月，镜中花”。因此，训练数学语言表达能力，让学生说出概念和概念的关键词，以及说出公式、法则和性质的具体内容，是概念教学的重要过程。

例如：在教学“比的基本性质”这一课时，就要充分利用学生已有知识，精心安排“说一说”的活动，使学生在联想、猜测、观察、对比、类推等过程中总结出概念，巩固和加深所学新知。

师：同学们，你们能说一说比的性质是什么吗？

生1：比的前项和后项同时乘或除以一个相同的数（0除外），比值不变。

师：那你们能不能举例论证说一说比的性质呢？

生2：我是这样论证的，因为4∶6=4÷6=2/3 ，而8∶12=8÷12=2/3，所以4∶6=8∶12。从中可以看出，比的前项和后项都扩大了2倍，比值没有变化。

生3：我是这样想的，比的前项相当于除法中的被除数，比的后项相当于除数，比值相当于商，由此推断出比的基本性质。

生4：根据比与分数之间的关系可以知道，比的前项相当于分数中的分子，后项相当于分母，比值相当于分数值。对比分数的性质，可以得出比的基本性质。

师：同学们说得都很好。

在这个教学片断中，学生根据商不变的性质和分数的基本性质进行大胆探索交流，让数学课堂更富含“数学味”。因此，在概念教学中重视“说”的训练，能提升学生的迁移能力和概括归纳能力。

三、解决问题中的“说”

1.说图意

出示主题图，让学生先观察，然后要求学生说一说看到了什么？编一个小故事，提一个相关的数学问题，促使学生有话可说。

例如，三年级上册的“找规律”，教材中出示了一张图片，我们可以让学生先仔细观察图片，再和学生谈话：看了这幅图，谁能编个好听的故事给大家听呢？

生：兔妈妈和兔宝宝们住在美丽的大森林里，它们一起游戏，一起学习，手帕脏了，就洗了晾起来，大灰狼来了，它们一起打木桩做陷阱，相亲相爱地生活在一起。

学生编完小故事，老师接着问：从图中你知道了什么？你想提哪些数学问题？

生：兔子晒了多少块手帕？用了多少个夹子？

生：有几个蘑菇？有几只兔子？

生：有多少块篱笆？有多少根木桩？

……

数学中的“说”具有举足轻重的作用，让学生在情境中去发现，去寻找数学问题，成为一个数学问题的发现者，既符合儿童的心理特点，也能调动学生“说”的积极性，让学生感受到数学就在身边，从而有效促进学生积极主动地参与到学习活动中，最终达到核心素养下的培养目标。

2.说思路

在解题时，由于学生掌握的知识程度不同，思维发展水平不同，学生会从不同的角度去思考问题，因此在教学“解决问题”时，可让学生独立思考，认真分析，说一说解题思路与方法，通过“说”发展思维，疏通思路。

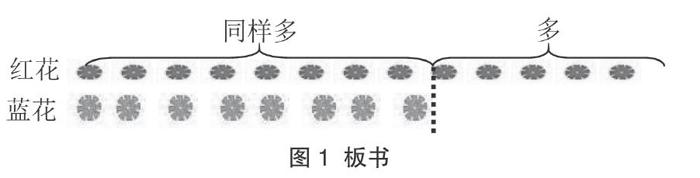
例如，在教学一年级下册“解决两数相差多少的实际问题”时，出示：红花13朵，蓝花8朵，红花比蓝花多多少朵？

生1：我是这样想的，要求红花比蓝花多多少朵，“多”是指红花的朵数与蓝花一个对一个，对完后还多出来的部分就是红花比蓝花多的朵数，所以用减法计算。

生2：我们要求红花比蓝花多几朵，就可以从13朵红花里拿掉和蓝花同样多的8朵，剩下的就是红花比蓝花多的5朵，所以用减法计算。

板书形成（图1）。

课堂中普遍存在一个问题，就是教师将自己的思路直接讲给学生听，而且越到高年级这种现象就越严重，導致学生对解题思路还停留在一知半解中。所以，在解决问题教学时，先让学生独立思考，明确题中的数量关系，说一说解题思路，从“说”中发展智力，以说促思，让学生真正理解所学知识，体验成功的愉悦。

四、规定知识中的“说”

学生的数学学习从某种意义上说，是一种体验，正所谓“手脑并用听说写，心中悟出始知深”[4]。在规定知识教学中，往往都是老师讲、学生听，结果一节课下来，老师讲得口干舌燥，学生听得云里雾里。这就更需要让学生来说一说，便于学生观察规律、发现规律和掌握规律。

例如，三年级下册的“年月日”第二课时“平年闰年”的教学，教师先出示2005年至2016年的2月份月历卡。

师：观察月历卡，根据每年二月的天数，找一找，哪些年份是平年？哪些年份是闰年？并在年份的旁边用“平”或“闰”标出来。

学生自主判断，教师巡视指导，指名汇报。

根据学生的汇报，教师板书（图2）。

师：从2005年开始，大家读一读平年和闰年的排列，说说有没有什么规律呢？

学生读着读着，不一会儿全班学生就都有节奏地齐声读出来。

师：谁来说一说，有什么规律呢？

生1：平平平闰    平平平闰    平平平闰

生2：它们是按“平平平闰”四个为一周期依次不断重复出现。

（教师板书圈出：平平平闰）

“语言是思维的外壳”，让学生以读助找，并说一说规律，抓住了以上关系，就抓住了本质，不管题目怎么变化，都可以以不变应万变。当学生能按照“平平平闰，平平平闰……”这样每四字一顿、有节奏地说出来时，就充分说明学生已经发现了平年和闰年的排列规律，为以后的学习打下了良好的基础。

总之，在课堂教学中，要注重让学生张开嘴巴“说”，激发学生“说”的兴趣，挖掘学生“说”的动力，使他们想说、爱说、会说，经历获取知识的思维过程，把教学建构在核心素养的培养上，让数学课有一定的“深度”与“厚度”。

【参考文献】

肖红梅.精心培养一年级孩子倾听的良好习惯[J].发现，2018（13）：8.

邵瑞珍.教育心理学[M].北京：高等教育出版社，1999.

陈华忠.加强“说”的训练，培养表达能力[J].小学教学设计， 2014（02）：7-9.

张秀琴.体验，展现数学的魅力[J]. 理科爱好者（教育教学版），2009，1（01）：96.