“基于问题和任务”教学模式的探究

高路 王乾生 林军

[摘要]“以任务探索生成问题，以问题思考形成知识，以文化渗透丰富內涵”的课堂教学模式，体现以学生发展为本的现代教育理念，可极大提高课堂教学效率。

[关键词]任务，问题，文化，曲线与方程

[中图分类号]G633.6[文献标识码]A [文章编号]1674-6058（2020）11-0005-03

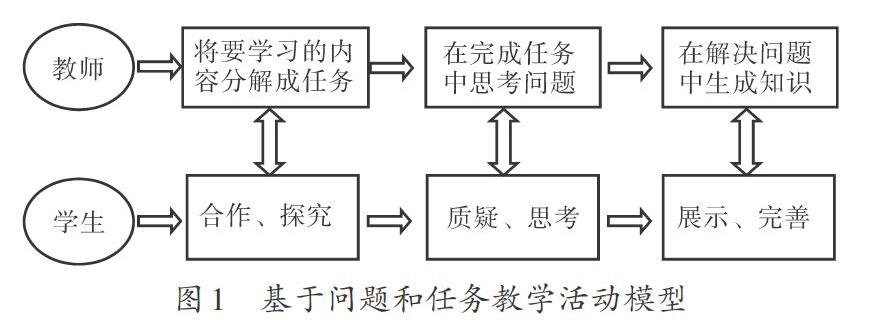
广西普通高中学科基地建设柳州高级中学数学课程基地自建成以来，以探索适合学生发展的、有数学味的高效课堂为建设目标，形成了以“以任务探索生成问题，以问题思考形成知识，文化渗透丰富内涵”的课堂教学模式（如图1）。

2019年11月20日，我校高路老师参加柳州市青年教师赛教课，课题是《曲线与方程》，教学设计采用“基于问题和任务”的教学模式，得到评委及听课教师的一致好评，获得了柳州市青赛课一等奖，以下是本节课的课堂实录，希望通过实录这种形式，能更加直观地让一线教师了解此教学模式的基本步骤和实施路径。

[课堂实录]

一、创设情境，丰富内涵

师：人类对曲线与方程的认识经历了一个漫长的过程，下面请同学们观看视频，看看费马和笛卡尔研究曲线的方法，与阿波罗尼奥斯有什么不同。

（学生观看视频）解析几何的发展史，

1.古希腊数学家阿波罗尼奥斯采用平面切割圆锥的方法，得到了圆、椭圆、双曲线、抛物线，并从纯几何的观点研究了圆锥曲线的性质，后人几乎无法突破。

2.费马，17世纪法国数学家，通过引进坐标，从方程出发研究几何曲线的轨迹。

3.几乎同一时期，法国另一位数学家笛卡尔，引入坐标法，从轨迹开始建立方程。

虽然费马的研究是从数到形，笛卡爾是从形到数，但他们都建立了坐标系，引入坐标，将方程与曲线联系起来，创立了解析几何。

设计意图：将数学史融入课堂，链接了章导言，既激发了学生的学习热情，又让学生了解数学家研究曲线的方法，使课堂的文化味更浓。

二、自主探究，生成概念

任务活动一：请在平面直角坐标系中，画出方程2x²-y=0（x≠0）对应的曲线，并思考：

问题1：你用了什么方法画曲线？

问题2：曲线上的点坐标从何而来？

生：问题l是采用描点法，

生：问题2是从方程的解中选取，

师：刚才有些同学没有在曲线中挖掉原点，为什么要挖掉原点？

生：因为题设要求x≠0.

师：若不挖掉原点，从图形直观来看，以方程的解为坐标的点与曲线上的点相比，谁多谁少？

生：点多解少。

师：我们只是选取了几个点描出曲线的大致图形，是否可以认为以这个方程的所有解为坐标的点都在对应曲线上，这样的猜想合理吗？

生：我们作图都用描点法，这当然是对的，

为了验证猜想，学生给出方程的任一组解，教师用几何画板演示以这些解为坐标的点都在曲线上，

师（追问）：若以方程的解为坐标的点都在曲线上，则谁的点的个数有可能多？

生：曲线上的点有可能多。

师：此时，若把方程的解集和曲线上的点集分别用集合A、B表示，A、B有什么关系？

生：A是B的子集。

设计意图：让学生经历描点法作图，能更直观地体会以方程的解为坐标的点都在曲线上，实现从数到形的转化，为学生理解方程的曲线这一概念提供实例。

任务活动二：求如图2所示的曲线对应的方程，并思考：

问题3：你是用什么方法求方程的？

生：直线过（-2，0）和（0.2），我是将两点代人斜截式求出直线方程x-y+2=0（x≠1）的，

师：你能否保证直线上所有点的坐标都满足你选用的这两点所求的方程？

生（迟疑后）：应该是吧。

教师操作几何画板，在曲线上任取一点，度量其坐标，让学生充分感知，不管点如何移动，点坐标始终满足所求方程。

师：如果所求方程没有限制x≠-1.显然，方程的解比曲线上的点多，若曲线上的点坐标都是方程的解，则谁的个数有可能多？

生：解有可能多。

师（追问）：此时，若把方程的解集和曲线上的点集分别用集合A、B表示，A、B有什么关系？

生：B是A的子集。

设计意图：让学生经历求直线方程的过程，学生能更直观地体会曲线上的点坐标都满足方程，实现从形到数的转化，为学生理解曲线的方程这一概念提供实例。

任务活动三：请分别画出曲线C：到坐标原点距离为1的圆在y轴右侧部分，和方程f（x，y）=O：x²+y²=1（y>0）表示的曲线，并思考：

问题4：曲线C上的点集A与方程f（x，y）=0的解集B有包含关系吗？

生：没有。

师：这样两者间不能建立某种对应关系。

设计意图：对概念的理解不光要深究其內涵，还要明白其外延，提供方程的解集与曲线的点集间没有相互包含关系的实例供学生辨析是很有必要的。

师：通过这三个例子，请大家想一想，要使方程与曲线能够相互表示，以方程的解为坐标的点与曲线上的点间应该能够建立怎样的对应关系？（学生小组讨论）

生：方程的解与曲线上的点一样多。

师：对，一点不多，一点不少，那么我们能否将“方程的解与曲线上的点一样多”这一条件更加“数学化”

一点呢？（学生回答，互相补充）

（教师板书方程与曲线的定义）

设计意图：通过提供丰富的实例去揭示概念的本质属性，从而促成概念的生成。

三、深化概念，巩固内化

任务活动四：判断图3的方程能否叫作曲线的方程，曲线能否叫作方程的曲线，并思考：

问题5：当方程与曲线不一致时，你能否修改曲线或方程中的一个，使得方程变成曲线的方程，曲线变成方程的曲线？

设计意图：通过修改方程或曲线中的一个，使二者能建立一一对应关系，这是对方程与曲线概念的再認识与升华。

师：任务活动四要判断曲线与方程不对应，只需举反例，但要说明题（4）中方程与曲线是一一对应的，就必须严格加以证明，那么如何证明呢？

生：从曲线和方程定义的两个方面进行，

师：请完成下列作业。

证明：以坐标原点为圆心，半径等于1的圆的方程是x²+y²=1.

（给学生充分的时间思考后，请一个学生展示其证明过程）

生（恍然大悟）：点（X₀，Y₀）到原点的距离等于1.所以方程的解为坐标的点在圆上，

师：在上述证明过程中，无论是取圆上一个点，还是取方程的一组解都是任意的，并且都满足曲线和方程定义的两个方面，所以我们就严格证明了该命题，

设计意图：本教学环节的设计，一是让学生明白数学是严谨的，当你肯定一个问题时，就要给出严谨的证明;二是让学生学会证明方程与曲线的关系，进一步理解方程与曲线的概念，学会数与形间的转化。

四、课堂小结，总结提升

师：本节课我们收获了哪些知识？用到了什么思想方法？

（学生谈体会谈感受，相互补充，如图4）

师：方程与曲线是整个解析几何的基石，把曲线用方程表达，就为我们用代数方法研究几何问题提供了有力的保障，为接下来进一步研究圆锥曲线奠定了基础。

设计意图：课堂小结是对一节课的一个高度概括，有助于学生理顺知识，形成方法，深化概念，提升能力。

五、作业布置（略）

[教学反思]

1.社会的发展带来育人观念的转变，数学文化融入课堂成为必然，曲线与方程有着丰富的数学文化背景，以解析几何发展史为素材引入新课，让学生了解数学家研究手段的变迁，感知数学思想，

2.任务设计强调目的性与针对性，曲线与方程的概念是非常抽象的，学生难以理解，但这个概念兼具形与数的特征，所以设计任务活动一、任务活动二、任务活动三的目的就是实现从数到形、形到数、数形互化的转变，实例典型丰富，引起学生的认知冲突，利于学生数学抽象素养的养成，任务活动四通过辨析正、反两方面的实例，不仅需要判断，还需要严谨论证，这对培养学生的逻辑推理能力意义重大。

3.问题设计有启发性和思考价值，由任务引出的问题从学生思维的最近发展区出发，激发了探索欲望，启发学生思考，充分暴露其思维过程，落实重点，化解难点，提高了课堂教学效率。