结合分数阶微分及Retinex的NSCT自适应低照度图像增强
林剑萍,廖一鹏
(1. 阳光学院 人工智能学院,福建 福州 350015;2. 福州大学 物理与信息工程学院, 福建 福州 350108)
1 引 言
低照度图像对比度较低,细节丢失严重,不利于人眼观察和计算机视觉算法的使用。因此,有效的图像增强算法对后续图像分析和图像理解非常重要。
图像增强的主流算法包括:直方图均衡化、Retinex、分数阶微分、模糊集理论及多尺度变换等[1-2]。直方图均衡化的增强算法,整体对比度有明显提高,但会出现过增强、微弱信息被丢失的情况[3-5]。万智萍[6]等提出的结合人眼视觉特性与直方图均衡化的增强算法,改善了图像的整体视觉效果,但不可避免地出现微弱信息丢失、放大噪声以及局部信息被弱化等情况。Land[7]等人提出的 Retinex 理论被广泛用于图像增强,其中最经典的是单尺度 Retinex(Single scale Retinex,SSR)[8]与多尺度 Retinex(Multi-scale Retinex,MSR)[9]算法,它们均以高斯滤波器作为低通滤波器, 虽然算法简单,但增强后的图像光晕现象严重,且算法是基于时域的增强方法,处理低照度图像时会出现细节丢失、边缘模糊等现象。Elad[10]等提出基于双边滤波(bilateral filter)的 Retinex 算法, Wang[11]等提出基于引导滤波(guided filter)[12]的 Retinex 算法, 张诗[13]等提出的基于Retinex的引导滤波变分框架低照度图像增强算法, 尽管这些滤波器具有一定的保边平滑能力, 但在维持保边能力的同时难以做到对图像充分平滑, 使得照度图像估计仍然存在偏差。云海姣[14]等人提出了结合直方图均衡和模糊集理论的红外图像增强,克服了过增强和局部信息被弱化等问题,但是在计算能力、去模糊化等方面的效果仍有待加强。国外学者提出多尺度理论后,基于变换域如Wavelet 变换、Contourlet 变换及非下采样 Contourlet 变换的增强算法大批涌现。在国内,朱国庆[15]等人提出一种基于人类视觉系统的亮度掩蔽和对比度掩蔽特性的NSCT 域红外图像增强算法, 该算法能够有效地对图像局部和整体进行增强, 同时能够避免产生过增强现象,但图像纹理细节还不够丰富。陈庆利[16]等人提出的基于分数阶微分的增强算法,能使纹理细节信息丰富,但整体动态范围呈现压缩趋势,不便于人眼观察。朱丹丹[17]等人提出了Contourlet变换和遗传算法相结合的沥青红外图像增强方法,能有效地抑制噪声,提高清晰度,但会出现“混叠”现象。曹美[18]等人提出的基于非下采样 Contourlet 变换的增强算法,并结合直方图均衡化,能有效提高图像的整体效果,同时能抑制噪声的放大,但对局部的增强不太理想;Cao[19]等人提出了基于NSCT和分数微分的深度图像增强与检测方法,该方法能有效地增强图像的深度和检测噪声,但在处理复杂物体和室外光线情况时仍然是一个挑战。
针对上述算法的不足,本文结合NSCT变换和改进的Retinex、分数阶微分,对低照度图像进行多尺度增强处理。首先将图像NSCT多尺度分解,获得低频子带图像和高频子带系数,结合改进的Retinex算法对低频分量进行增强,提高图像轮廓的清晰度,扩展其灰度级的动态范围;然后将高频经Bayes阈值隔离噪声后利用自适应分数阶微分进行增强,提升图像的边缘和纹理细节;最后对处理后的图像进行NSCT重构,获取增强后的低照度图像。将本文算法与其他增强算法进行主观与客观的对比和分析,本文算法克服了上述算法存在的光晕现象、模糊现象、细节丢失和“混叠”等现象,改善了图像整体的视觉效果。
2 NSCT域低照度图像增强
2.1 低照度图像NSCT分解
Contourlet 变换能较为理想地描述或表征光滑曲线的边缘,但不可避免地产生频谱混叠失真现象。NSCT变换主要是通过一种迭代方式获得多分辨率、高冗余度、多方向及各向异性的表示方法[20]。在分解和重构过程中,都没有涉及到下采样,使其拥有平移不变性。NSCT变换的结构与Contourlet变换类似,如图1所示。

图1 NSCT变换三级分解结构图Fig.1 Three-level decomposition structure of NSCT transform
NSCT变换根据独特滤波构造实现多尺度分解,首先由NSP对输入图像进行塔形分解,得到低频子带和多个带通子带,然后采用非下采样方向滤波器组(NSDFB)对各个带通子带进行多方向分解,得到多个不同方向的高频子带图像,最后得到一个低频近似图像和多个不同尺度方向的高频子带图像,而且这些图像的分辨率都和原始图像相同。
2.2 低频子带改进双边滤波Retinex增强
一般情况,待处理图像经过 NSCT 变换分解得到的低频分量集中反映的是大量的基本信息,也就是其轮廓,一般不含有噪声。因此,对低通子带系数处理的关键是要扩展其灰度级的动态范围。相比于传统的线性、非线性算法只能增强图像的某一特征,Retinex 算法可以在颜色恒常、对比增强、动态范围压缩等方面达到平衡,增强效果尤为显著[21],故本文采用 Retinex 算法并加以改进。
Retinex 模型对理想图像的定义,可以表述为:
f(x,y)=r(x,y)×i(x,y),
(1)
式中:f(x,y)为理想图像;i(x,y)为照度图像,其根据场景的不同照明程度而变化;r(x,y)为反射图像,其与场景本身的自然属性相关,通常体现的是场景的细节特征,与照度分量没有丝毫的相关性。
Retinex图像增强的目的就是从待处理图像f中估计出照度图像i,同时去除照度分量信息i,从而分解出反射图像r,消除或降低光照不均的影响,以改善图像的视觉效果。一般做法是:将图像转至对数域,从而将乘积关系转换为和的关系,如式(2)所示;然后归一化去除图像照度分量;将去除了照度分量的图像求指数,反变换到实数域后输出。
lg[f(x,y)]=lg[r(x,y)×i(x,y)]=
lg[r(x,y)]+lg[i(x,y)],
(2)
算法流程如图2所示。

图2 Retinex算法流程图Fig.2 Algorithm flow char of Retinex
一般的Retinex算法在对光照图像估计时,都会假设初始光照图像是缓慢变化的,即光照图像是平滑的,但实际情况并非如此,在亮度相差很大的区域边缘处,图像的光照变化是不平滑的,在这种情况下,Retinex算法在此区域会出现 “光晕”现象。
本文对Retinex算法进行改进,具体如下:
借助非线性的双边滤波函数估计其照度分量。通过空间邻域滤波器和值域滤波器进行光照强度的改变,双边滤波算法定义为:
(3)
归一化函数表述为:

(4)
式中:f(x)表示原始图像在点x处的灰度值,h(x)表示输出图像在点x处的灰度值,g(φ,x)表示临近点φ与中心点x之间的距离相似程度,s(f(φ),f(x))表示临近点φ与中心点x之间的灰度相似程度。双边滤波的距离相似度和灰度相似度都取参数为欧氏距离的高斯核,具体如下:
(5)
式中,d(φ,x)=‖φ-x‖表示φ与x两点之间的欧式距离。
(6)
式中,δ(φ,f)=‖φ-f‖表示φ与f2个灰度值之差。
照度分量表示图像的动态范围,需对其进行校正。Gamma校正(幂律变换)是一种重要的非线性变换,是对输入图像灰度值进行指数变换,可以提高图像的动态范围,主要运用在图像增强,目标检测及图像分析等领域。本文采用Gamma校正函数校正照度分量。表示如下:
(7)
式中:γavg′为校正后的照度分量,γ1、γ2分别为两滤波器的照度,Kavg为自变量Kavg1、Kavg2由人为进行设定。
反射分量中也存在许多重要特征信息,适当的校正可以丰富其层次性,本文利用影响因子对其进行校正,校正公式表述为:
ϑ′=α×ϑ,
(8)
式中:α为影响因子,即增强的倍数,ϑ为反射分量。
改进Retinex算法的实现如图3所示。先将图像转至对数域,借助非线性的双边滤波函数进行照度估计,然后利用Gamma校正函数,对输入图像的照度分量灰度值进行指数变换,完成照度校正;将去除了照度分量的图像求指数,反变换到实数域,利用影响因子校正其反射分量;最后将校正过的照度分量和反射分量相乘后输出。该算法增强了图像的整体轮廓,扩展其灰度级的动态范围,克服了光晕和模糊现象。

图3 改进Retinex算法的实现Fig.3 Implementation of improved Retinex
2.3 高频子带的自适应分数阶微分增强
经过NSCT变换分解得到的高频方向子带系数往往包括大部分的边缘信息、纹理细节及几乎全部的噪声。一般情况下,复杂纹理和细节及弱边缘特征信息出现在子带绝对值较大的系数间,故需要将其进行保留或增强处理,而噪声存在于高频子带中绝对值较小的系数中,会影响图像整体效果,需加以抑制。为了达到更为理想的增强效果,将分解得到的高频子带系数进行Bayes Shrink阈值处理,不同尺度、不同方向上小于阈值的系数将其置0,对大于阈值的系数进行保留,并对保留后的系数利用改进分数阶微分算法做进一步的增强处理。
2.3.1 Bayes Shrink阈值去噪
由Bayes Shrink阈值函数T构造得:

(9)
式中:Zj,k(m,n)为第j尺度、第k方向的NSCT系数,Tj,k(m,n)为局部阈值,其计算公式如式(10)所示:
(10)
式中:σj,k为噪声的标准差,σz(m,n)为信号的局部标准差,其计算公式如式(11)和式(12)所示:
(11)

(12)
2.3.2 改进分数阶微分算法
目前Riemann-Liouville(R-L)定义、Grumwald-Letnikov(G-L) 定义、Caputo定义是比较经典的分数阶微分定义。在数字图像处理中, G-L 定义得到广泛的应用,其数学表达式为:
(13)
其中:D表示此式为分数阶微积分,GL表示该分数阶微分采用Grumwald-Letnikov(G-L)定义,h表示积分时间步长。
若f(t)的持续期t∈[a,b],将函数持续期间[a,b]按单位间隔h=1进行等分,得到:
(14)
则一元函数f(t)的v阶分数阶微分差分表达式为:

(15)
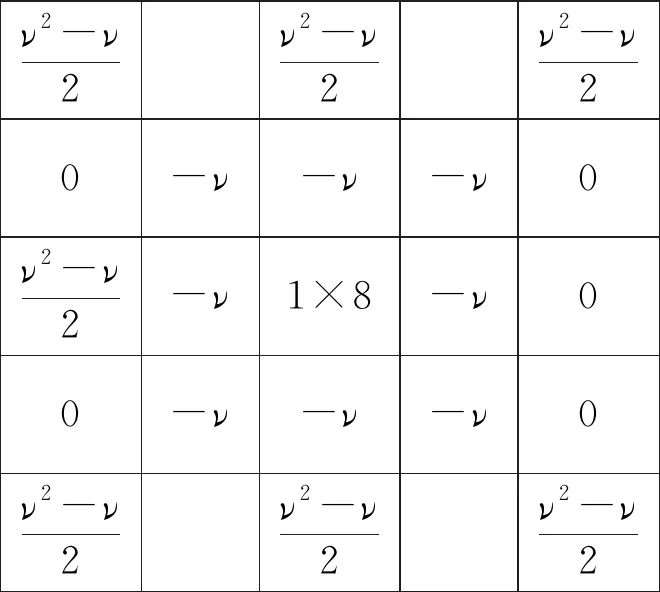
求取5×5八方向的分数阶微分掩膜算子,并叠加得到图4所示的掩膜。
ν2-ν2ν2-ν2ν2-ν20-ν-ν-ν0ν2-ν2-ν1×8-ν00-ν-ν-ν0ν2-ν2ν2-ν2ν2-ν2
图4 8个方向偏微分叠加后的掩膜
Fig.4 Mask superposed by partial integrals of 8 directions
文献[22]、[23]证明,相较于整数阶微分,分数阶微分进行边缘检测时,不仅能够很好提取图像边缘信息,而且还能够对平滑区域的弱边缘信息有很好的保留。
(1)Otsu算法选取最佳阈值
阈值的选取尤为关键,阈值的好坏直接决定了图像的增强效果。Otsu算法即最大类间方差法,其鲁棒性强、实时性和精准性高[24]。但传统的二维Otsu算法难以精准识别图像的边缘和纹理信息。李博[25]等对传统的二维Otsu算法进行改进,以所选图像的梯度为对象,关联像素点与邻域像素点的信息,同时构建二维直方图,并借助整体轮廓与边缘细节的类间方差的极大值获得最优阈值。
对于待处理图像f(i,j),L为灰度级数,M(i,j)为像素点(i,j)各方向上梯度平均值的集合统称,N(i,j)为像素点(i,j)各邻域梯度的平均值。
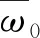
(16)
(17)
上面两式所对应的均值μ0与μ1分别表述为:
(18)
(19)
由μ0与μ1两向量构成的二维直方图的均值μT可表述为:

(20)

由于分布在对角线位置的数值较小且对最终的结果影响不大,故可忽略不计。因此,类间的散度矩阵SB即最佳阈值,可表述为:
(21)

(2)确定最优阶数v进行自适应增强


(22)

图5 自适应分数阶微分算法的实现Fig.5 Implementation of adaptive fractional differential algorithms
自适应分数阶微分算法的实现如图5所示。求待处理图像f(i,j)像素点(i,j)各方向上梯度平均值的集合M(i,j),像素点(i,j)各邻域梯度的平均值N(i,j)。利用Otsu算法选取最佳阈值S,再用构造的分数阶微分的分段函数优化分数阶微分的阶数v,再把v代入掩膜算子,从而实现对分解获得的高频方向子带系数进行自适应分数阶微分增强。
3 本文算法流程与步骤
综上分析,文中低照度图像多尺度增强算法流程如图6所示,具体实现步骤如下:
Step 1:经配准、校正等预处理后,采用NSCT变换对原始图像进行多尺度多方向的分解;
Step 2:经NSCT多尺度变换分解后,得到低频子带近似分量,并根据双边滤波器的特性来估计照度分量,同时反射分量与照度分量借助影响因子α、Kavg来分别进行校正,从而对低频子带系数实现改进Retinex算法的增强;
Step 3:求取像素梯度均值M和邻域梯度均值N,根据二维Otsu算法选取最佳阈值S,并通过式(18)设定的分段函数来优化分数阶微分的阶数v,从而对分解获得的高频方向子带系数进行自适应分数阶微分增强;
Step 4:对处理后的低频子带系数和高频方向子带系数进行NSCT反变换,从而获得增强后的图像。

图6 本文增强算法流程图Fig.6 Flowchart of strengthened algorithm in this paper
4 实验仿真结果与分析
本文从Athena摄像机系统注册的数据库图像中,选取不同场景的2幅红外夜视图像和2幅低亮度可见光图像分别进行仿真实验,如图7和图10所示。实验在台式机(Windows 10操作系统,CPU:Pentium,RAM:4 GB)上采用Matlab R2016a软件进行仿真。其中,小波变换采用“db4”小波包进行4层分解,而Contourlet变换以及NSCT变换均采用金字塔滤波器为“9-7”滤波器,方向滤波器组采用“dmaxflat”滤波器,分解的尺度均设定为3级,且每一级分解后所对应的子带方向数分别为2,4,8。实验过程中,为了更好地评判所提算法是否具有优越性,本文将此算法与CLAHE(Contrast Limited Adaptive Histogram Equalization)算法、FD(fractional differential,v=0.6)算法、MSR(Multi-Scale Retinex)算法、基于Wavelet变换算法、基于Contourlet变换算法、基于NSCT变换算法、文献[14]算法以及文献[15]算法进行对比实验,首先从人眼视觉感知的主观角度进行效果描述,再借助对比度(CR)、清晰度(AG)以及信息熵(IE)进行客观分析。对比度大的图像通常层次感强,清晰度高,其计算公式为:

(a) 实验图像1(a)Experimental image 1

(b) 实验图像2(b) Experimental image 2
(23)
其中:δ(i,j)=|i-j|,即相邻像素间的灰度差,pδ(i,j)即相邻像素间的灰度差为δ的像素分布概率。清晰度是图像的平均梯度,可以敏感地反映图像对细小反差表达的能力,可用来评价图像的清晰程度,同时反映出图像中微小细节反差和纹理变换特征。其公式为:
(24)
其中:F为目标图像,M、N分别为图像F的行数与列数。
信息熵的定义为:
(25)
对于一幅单独的图像,可以认为其各像素的灰度值是相互独立的样本,则这幅图像的灰度分布为p={p0,p1,…,pi…,pL-1},pi为灰度值等于i的像素与图像总像素之比,L为图像总像素的灰度级。
4.1 红外夜视图像增强效果分析
通过图8可以发现,图8(a)相比于原始图像,好像去了层“雾”,目标行人也较为清晰,但筑台周边的沙堆纹理等细节不易识别;图8(b)中的目标行人还算清晰,筑台的黑色纹理容易识别出来,但整体对比度偏暗;图8(c)中的目标行人清晰可见,沙堆纹理也有一定凸显,但引入了部分噪声造成沙堆模糊化;图8(d) ~(f)是基于多尺度几何变换实现的,取得了一定的效果,纹路也更为细腻,但增强效果还有待进一步提高;图8(g)和图8(h)相比于前面几幅图,效果更为显著,其在增强对比度的同时能保留较多的纹路信息。但本文算法(图8(i))能更有效地改善图像的动态范围,灰度色彩更为饱满,如行人及筑台黑色条纹清晰可见,弥补了类似过增强、细节丢失、局部信息被弱化及模糊化等不足,更具有丰富的边缘、细节等特征信息,如筑台两侧的石头能清楚地辨识。



图8 红外图像1用不同增强算法的效果对比图Fig.8 Comparison map of infrared image 1 processed with different enhancement algorithms
从表1中的数据也可以发现,各种算法的对比度、清晰度及信息熵呈现逐渐提高的态势,且本文算法的3个评价参数的数值均要高于其他几种增强算法,相比于增强效果较为显著的文献[15],对比度、清晰度及信息熵分别提高了10.4%,11.6%,2.5%。正好印证了主观上的效果评价,可以让图像看起来更自然,更符合人眼视觉的直观感受。
表1 各种算法处理实验图像1后的客观数据
Tab.1 Objective data of experimental image 1 processed with various algorithms

算 法对比度清晰度信息熵CLAHE11.617.946.85FD(v=0.6)12.778.576.99MSR13.188.847.04Wavelet变换17.5410.997.23Contourlet变换18.3111.137.33NSCT变换19.3311.257.38文献 [14]20.5211.517.46文献 [15]30.0715.967.57本文算法33.2117.817.76
通过图9可以发现,相比于原始图像,图9(a)能较好地去除“白雾”,有一定的增强效果,房屋、树木及栅栏较清晰,但路面的纹路丢失严重;图9(b)的视觉效果还可以,且比图9(a)具有更为丰富的路面纹理特征,但整体视觉效果有待改善;图9(c)中的云层、房屋、树木以及栅栏清晰可见,路面纹理也有一定的凸显,但顶部背景信息偏暗;图9(d)~(f)均取得了一定的效果,纹路也较为细腻,但动态压缩范围有待提高;图9(g)和图9(h)的路面纹理脉络较细致,能给人直观的画面感。但本文算法(图9(i))整体效果更为清晰可见,且道路纹理、道路中的白带及屋顶的乌云边缘等纹理均能很好地展现给观察者。从客观角度出发,表2中的数据可以发现,本文算法的对比度、清晰度及信息熵也均高于其他几种增强算法,相比于文献[15],对比度、清晰度及信息熵分别提高了9.6%,11.2%,1.4%,这对后续的识别、跟踪及特征提取极为有利。



图9 红外图像2用不同增强算法的效果对比图Fig.9 Comparison map of infrared image 1 processed with different enhancement algorithms
4.2 低亮度可见光图像增强效果分析
与红外图像增强效果类似,图10(a)中的原始图像好像被蒙上了一层纱,草丛中的细节信息也被“白雾”化。处理后,通过图11可以发现,图11(a)中的树丛更为明朗,且飞机也更容易观察到,与此同时,草丛的弱纹理细节呈现“白雾”化,细节丢失严重;图11(b)能在去“雾”的同时,保留了草丛中的部分细节信息,但飞机、树丛等特征的亮度偏暗,让整体图像看起来不明朗;图11(c)与图11(b)相比,有相似的对比度,且纹理特征信息有所体现,但丢失了大部分的微弱信息;图11(d) ~(f)均取得了一定的效果,草丛纹路也较为细腻,但动态压缩范围有待提高;图11(g)和图11(h)中的草丛纹理部分脉络较细致,有一定的“还原”作用,能给人直观的画面感,但图11(g)的树木看起来不那么真实,会出现“闪烁”的白点,图11(h)中最右边的那棵树偏暗,与实际场景不匹配;本文算法避免了局部信息被弱化和细节不完整,图11(i)中的草丛更为饱满,飞机、草丛及树丛分布看起来更加自然。从表3中数据同样可以看出,3种参数呈现逐渐递增的趋势,且相比于文献[15]分别提高了13.4%,10.1%,1.5%,这与主观人眼察觉效果相匹配,进一步印证了本文算法的优秀特性。
表2 各种算法处理红外图像2后的客观数据
Tab.2 Objective data of infrared image 2 processed with various algorithms

算 法对比度清晰度信息熵CLAHE19.2110.357.63FD(v=0.6)21.7711.447.59MSR27.8512.927.57Wavelet变换28.4113.296.91Contourlet变换33.5314.967.51NSCT变换33.5714.867.69文献 [14]34.5816.317.65文献 [15]51.4521.597.72本文算法56.4124.017.83

(a) 实验图像1(a)Experimental image 1

(b) 实验图像2(b) Experimental image 2



图11 可见光图像1用不同增强算法的效果对比图Fig.11 Comparison map of visible image 1 processed with different enhancement algorithms
表3 各种算法处理可见光图像1后的客观数据
Tab.3 Objective data of visible image 1 processed with various algorithms

算法对比度清晰度信息熵CLAHE17.019.446.58FD(v=0.6)17.189.686.76MSR23.2511.747.31Wavelet变换23.3211.896.83Contourlet变换28.2214.577.27NSCT变换31.3516.397.46文献 [14]34.5814.427.56文献 [15]40.3219.267.46本文算法45.7121.217.57



图12 可见光图像2用不同增强算法的效果对比图Fig.12 Comparison map of visible image 2 processed with different enhancement algorithms
与图10(a)不同的是,图10(b)中原始图像的细节信息较不明显,如飞机的螺旋桨,由于飞行高度非常高,导致背景区域信息不易识别,如相间的山谷与山峰。通过图12中不同算法的实验仿真得知,图12(a)~(e)对背景信息有一定的增强效果,类似“网状”条纹能比较清楚地识别出,但机身、螺旋桨等目标信息看起来偏暗,导致整体视觉效果偏差;图12(f) ~12(h)相比于前面几种算法,它们均能近似还原飞机的原始模样,螺旋桨等细节信息也能很好地体现出来。因此,从主观上看不出本文算法的优势。通过表4中3个参数的数据得知,本文算法的数据最优,且相比于文献[15]分别提高了9.5%,6.4%,3.7%,能很好地说明本文算法优于其他算法。
表4 各种算法处理可见光图像2后的客观数据
Tab.4 Objective data of visible image 2 processed with various algorithms

算 法对比度清晰度信息熵算法对比度清晰度信息熵CLAHE16.898.745.91FD(v=0.6)19.889.736.67MSR21.4610.376.83Wavelet变换26.2111.816.72Contourlet变换27.9512.276.83NSCT变换28.6612.546.87文献 [14]29.7513.466.89文献 [15]37.1115.816.95本文算法40.6516.827.21
5 结 论
针对Retinex算法处理低照度图像时会出现细节丢失、边缘模糊等现象,文中提出了一种基于非下采样Contourlet变换、结合改进Retinex及分数阶微分的图像增强算法。采用改进的Retinex对低频子带图像进行增强处理,主要做法是引入非线性的双边滤波函数估计待处理图像的照度分量,并对处理后的照度分量及反射分量进行校正操作,消除了“光晕”现象的同时改善了图像视觉效果。针对传统固定阶次的分数阶微分算法存在的诸多缺陷,根据图像邻域分布特征,求取像素梯度均值及邻域梯度均值,通过二维Otsu算法获得最佳阈值,并通过预设定的分段函数确定最优阶数,自适应进行增强处理,使图像的边缘、纹理等细节更加清晰。实验结果表明,本文算法的对比度、清晰度及信息熵均高于其他几种增强算法,相比于文献[15]分别提高了10.7%,9.8%,2.3%。本文算法处理后的图像在细节、边缘保持等方面都优于其他算法,改善了图像视觉效果。

