深部岩体初始高构造应力场的3DEC模拟反演方法分析
郭延辉,李 靖,侯克鹏
(1.云南农业大学 建筑工程学院,昆明 650201;2.昆明理工大学 国土资源工程学院,昆明 650093)
初始地应力对于地下工程特别是深部采矿工程采场及围岩的稳定性具有重要的影响,是采矿工程设计和分析的基础资料[1]。开展现场地应力实测是获得矿区初始地应力场分布的最为直接的途径,然而受经费和场地等原因的限制,开展大规模的地应力测量并不现实,因此,通常地应力测量只能布置少数的测点[2]。通过少数地应力测点反演工程区地应力场的分布是科研人员最常用的方法,然而,由于地应力场成因十分复杂,影响因素众多,如何根据少量的地应力实测点反演矿区地应力场一直是采矿工程中面临的一个难题[3]。
关于地应力场反演方法的研究人们已经开展了大量的卓有成效的工作。汪吉林等提出了基于构造控制的地应力人工神经网络反演方法,反演结果与实测结果吻合度较高[4]。戚蓝等基于少数实测地应力数据,运用系统工程进行了地应力反演分析,取得了较好的效果[5]。易达等将遗传算法与有限元联合用于初始地应力场的反演分析[6]。李欣等对地应力反演分析时,发现采用改进的粒子群优化算法,地应力计算精度和效率更高[7]。饶运章等探究了利用FLAC3D应力边界组合来重构初始应力场的方法,结合龙门山矿区地应力场测量结果,验证了采用应力边界组合重构初始应力方法可行[8]。上述地应力场的非线性反演方法在反演复杂区域地应力场的时候具有一定优点,但是也存在参数选择过于依赖经验,并且相同的输入参数,其反演输出结果并不唯一的问题。近年来,由于数值模拟方法自身的优点广泛应用于深部岩体工程的数值模拟反演计算[9]。3DEC是一款基于离散单元法作为基本理论以描述离散介质力学行为的计算分析程序,其对于计算分析开采引起采空区围岩塌陷,地表沉降等问题等具有独特的优势[10]。然而目前关于运用3DEC反演模拟初始地应力场研究较少,特别是基于3DEC对深部岩体高水平构造应力场的模拟反演方法的研究鲜有报道。本文基于离散单元法3DEC,在对比分析位移边界条件和基于初始应变能理论的反演方法的基础上,探究深部岩体初始高水平构造应力场的反演方法,并将该方法应用于狮子山铜矿40号剖面高水平构造应力场的反演,进一步验证该方法的可行性。
1 计算模型构建及计算方案
计算采用离散单元法3DEC,计算模型长3 000 m,高1 400 m,宽50 m,按平面应变问题来考虑。计算
采用的模拟边界条件为:1)位移边界条件,即模型左右边界的水平位移约束,模型底部的位移固定,模型顶部设置为自由边界;2)基于初始应变能理论的初始高水平构造应力场的反演。地下开采引起围岩发生的变形破坏,其本质是能量转化的过程[9-10]。在开采过程中,围岩中所储存的弹性应变能随之变化,因此将构造应力作用下的岩体视为部分具有弹性体属性,在理论上具有合理性[9-11]。因此,基于3DEC反演高水平初始构造应力场时,可以将构造应力作为内力施加在模型内部,即在反演过程中,在位移边界条件的基础上,对模型内所有单元体采用梯形应力分布初值设置。数值模拟采用Mohr-Coulomb弹塑性本构模型。采用的宏观岩体力学参数为狮子山铜矿青灰色白云岩的岩体力学参数,见表1。计算模型及边界条件示意图见图1所示。
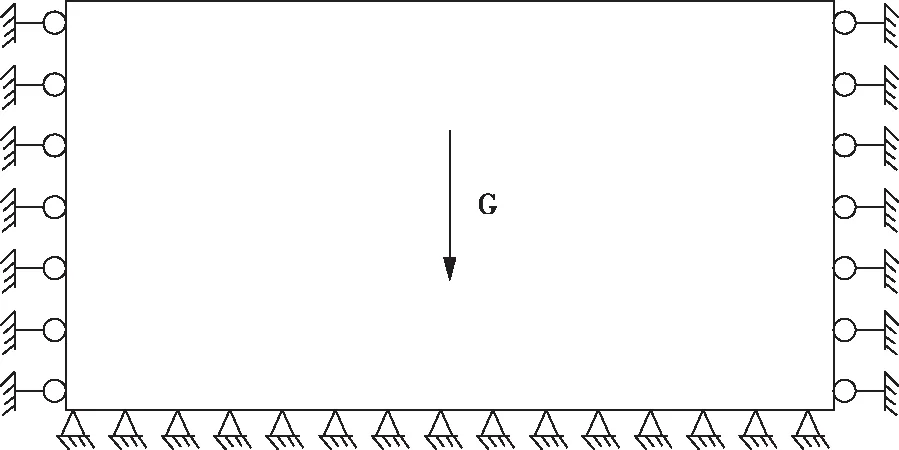
图1 计算模型及边界条件示意图Fig.1 Schematic diagram of calculation model and boundary conditions
2 应力场计算反演结果对比分析
2.1 基于位移边界条件的初始地应力场的反演
在位移边界条件下,计算反演得到的垂直应力和水平应力分布见图2和图3所示。计算结果表明,应力等值线基本呈水平展布,走向稳定,等值线间间隔几乎相等,无论是垂直应力还是水平应力,从地表至模型底部应力均呈线性增长分布,模型底部最大垂直主应力为38.79 MPa,最大水平主应力为11.598 MPa,模型底部最大垂直主应力为最大水平主应力的3.344倍。说明在位移边界条件下,生成初始地应力场中,自重应力占主导优势明显。由于3DEC采用凸多面体来描述介质中连续性对象元素(如岩块)的空间形态,所以等值线并不是完全为一条直线。同一高程的自重应力明显大于水平应力,最大主应力为竖直方向。初始地应力场中主压应力迹线分布结果也表明,相同埋深,最大主应力迹线垂直分量明显大于水平分量,最大主压应力数值随深度的增加呈线性增加。说明此种方法在模拟初始地应力场为自重应力时效果良好,但无法反演水平构造应力场。

图2 垂直应力分布Fig.2 Vertical stress distribution

图3 水平应力分布Fig.3 Horizontal stress distribution
2.2 基于初始应变能理论的高水平构造力场的反演
根据前面讨论,在位移边界条件的基础上,通过对模型内所有单元体采用梯形应力分布初值设置,来反演初始高水平构造应力场。反演分析得到的初始地应力场中的垂直应力和水平应力分布见图4和图5所示。从图上可以看出,垂直应力和水平应力从地表向下基本呈线性增加,垂直应力等值线水平展布较好,走向稳定。模型底部最大垂直主应力为39.062 MPa,最大水平主应力为65.095 MPa,最大水平主应力约为最大垂直主应力的1.67倍。但由于3DEC生成的凸多面体单元,因此垂直应力和水平应力等值线并非一条直线。同一埋深条件下,水平主应力明显大于垂直主应力。显然,最大主应力为水平方向,相同埋深下最大水平主应力与垂直应力的比值一定。初始地应力场主压应力迹线分布结果也明表明整个区域岩体中最大主应力均为水平方向,实现了水平构造应力为最大主压应力的初始应力场特征量的条件。
综上分析,应用离散单元法3DEC分析时,位移边界条件能够较好地反演自重应力场;而基于初始应变能理论的初始地应力场的反演方法,即在位移边界条件下,计算域内所有单元体采用梯形应力分布初值设置,即设定初始弹性应变能状态,使满足或拟合应力随深度变化的实测值,模拟效果与实际吻合最好,能够较好地模拟水平高构造应力场。

图4 垂直应力分布Fig.4 Vertical stress distribution

图5 水平应力分布Fig.5 Horizontal stress distribution
3 矿区岩体高水平初始构造应力场的反演验证
3.1 狮子山铜矿地应力场分布规律
狮子山铜矿位于云南省易门县小街乡,矿体倾角为70°~80°,矿体厚度为20~160 m,采用崩落法开采。矿区地应力实测结果表明矿区以近水平构造应力场为主,最大主应力方向垂直于矿体走向方向,最小主应力沿矿体走向方向,中间主应力为竖直方向[10]。最大主应力,中间主应力和最小主应力随深度的线性回归方程为:
σh,max=-0.016 3+0.051 1H
(1)
σh,min=-0.388 3+0.021H
(2)
σv=-0.601 8+0.030 7H
(3)
3.2 狮子山铜矿地应力场反演数值模型的构建与计算参数
以矿体为中心,选取矿区40号剖面作为计算剖
面,计算域垂直矿体走向方向取3 000 m,模型上边界取至地表,下边界取到地表以下1 400 m,即模型地表标高2 037 m,模型底部标高687 m;计算作为平面应变问题考虑,在矿体走向取厚度50 m。40号剖面分布有F2断层、F3断层、F4断层、FC2断层以及FC3断层,图6为矿区40号剖面断层与矿体分布示意图,图7为3DEC模型横剖面逻辑块体分布图。地应力按本文2.2节讨论的基于初始应变能理论的方法进行设置。
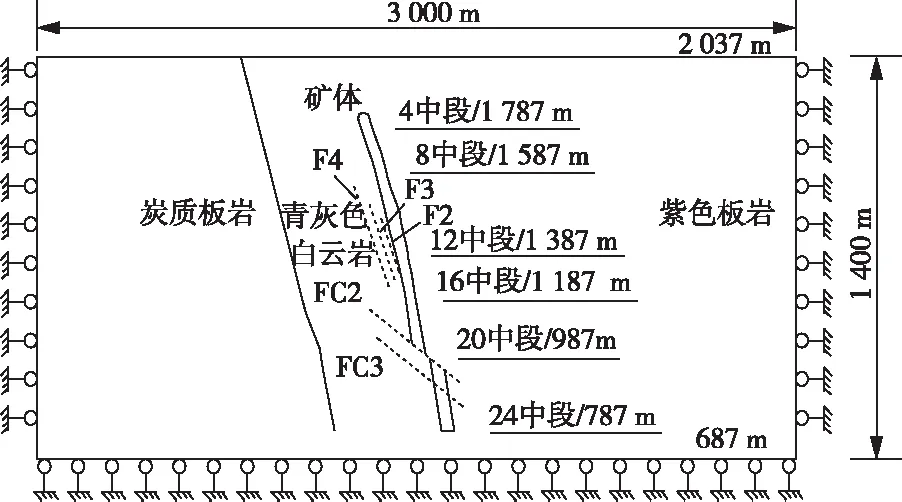
图6 断层与矿体分布示意图Fig.6 Distribution diagram of faults and ore bodies

图7 3DEC模型横剖面逻辑块体分布图Fig.7 3DEC model cross section logical block distribution
计算采用狮子山铜矿岩体力学参数,该参数是在室内岩石力学试验的基础上,结合岩体质量评价RMR值,采用Hoek-Brown准则,对岩石的力学参数进行工程折减弱化处理后得到的。各岩性宏观岩体力学参数见表1。断层的力学参数为:内聚力0.2 MPa,内摩擦角20°,剪切刚度0.60 GPa,法向刚度0.26 GPa,抗拉强度0.4 MPa。
图8和图9分别为初始应力平衡后模型最大主应力和最小主应力分布图,结果表明:1)初始应力场平衡后,最大主应力为水平方向,从地表向下呈线性增加,主应力迹线呈水平展布,应力云图中等值线间隔较均匀;2)在断层处应力场分布发生了异常,主应力迹线分布结果表明,断层处最大主应力平行于断层倾向,最小主应力垂直于断层,与断层对地应力场的阻隔效应有关;3)深部岩体的最大水平主应力和垂直应力反演值与实测地应力回归值之间的吻合较好。

表1 狮子山铜矿矿岩宏观岩体力学参数表

图8 最大主应力分布图Fig.8 The maximum principal stress profile

图9 最小主应力分布图Fig.9 The minimum principal stress profile
4 结论
1)运用离散单元法3DEC进行初始应力场反演,在位移边界条件下,应力等值线基本呈水平展布,走向稳定,等值线间间隔几乎相等,无论是垂直应力还是水平应力,从地表至模型底部应力均呈线性增长分布,模型底部最大垂直主应力为最大水平主应力的3.344倍。说明该边界条件下自重应力占主导优势明显,但是不能模拟初始高构造应力场。
2)采用基于初始应变能理论的初始地应力场的反演方法,即在位移边界条件下,将计算域内所有单元体进行梯形应力分布初值设置,在模拟初始高水平构造应力场时,同一埋深条件下,水平主应力明显大于垂直主应力,模型底部最大水平主应力约为最大垂直主应力的1.67倍。实现了水平构造应力为最大主压应力的初始应力场特征量的条件,表明该方法能够较好地模拟反演深部岩体初始高水平构造应力场。
3)将高水平构造应力场的模拟方法,应用于狮子山铜矿40号剖面高水平构造应力场的反演,计算分析表明深部岩体的最大水平主应力和垂直应力反演值与实测地应力回归值之间的吻合较好,可用于后续采动影响分析。
——以盈江地区5次中强震为例

